Improving performance of open-pit mine production scheduling problem under grade uncertainty by hybrid algorithms
来源期刊:中南大学学报(英文版)2020年第9期
论文作者:Kamyar TOLOUEI Ehsan MOOSAVI Amir Hossein BANGIAN TABRIZI Peyman AFZAL Abbas AGHAJANI BAZZAZI
文章页码:2479 - 2493
Key words:open-pit mine; long-term production scheduling; grade uncertainty; augmented Lagrangian relaxation; particle swarm optimization algorithm; bat algorithm
Abstract: One of the surface mining methods is open-pit mining, by which a pit is dug to extract ore or waste downwards from the earth’s surface. In the mining industry, one of the most significant difficulties is long-term production scheduling (LTPS) of the open-pit mines. Deterministic and uncertainty-based approaches are identified as the main strategies, which have been widely used to cope with this problem. Within the last few years, many researchers have highly considered a new computational type, which is less costly, i.e., meta-heuristic methods, so as to solve the mine design and production scheduling problem. Although the optimality of the final solution cannot be guaranteed, they are able to produce sufficiently good solutions with relatively less computational costs. In the present paper, two hybrid models between augmented Lagrangian relaxation (ALR) and a particle swarm optimization (PSO) and ALR and bat algorithm (BA) are suggested so that the LTPS problem is solved under the condition of grade uncertainty. It is suggested to carry out the ALR method on the LTPS problem to improve its performance and accelerate the convergence. Moreover, the Lagrangian coefficients are updated by using PSO and BA. The presented models have been compared with the outcomes of the ALR-genetic algorithm, the ALR-traditional sub-gradient method, and the conventional method without using the Lagrangian approach. The results indicated that the ALR is considered a more efficient approach which can solve a large-scale problem and make a valid solution. Hence, it is more effectual than the conventional method. Furthermore, the time and cost of computation are diminished by the proposed hybrid strategies. The CPU time using the ALR-BA method is about 7.4% higher than the ALR-PSO approach.
Cite this article as: Kamyar TOLOUEI, Ehsan MOOSAVI, Amir Hossein BANGIAN TABRIZI, Peyman AFZAL, Abbas AGHAJANI BAZZAZI. Improving performance of open-pit mine production scheduling problem under grade uncertainty by hybrid algorithms [J]. Journal of Central South University, 2020, 27(9): 2479-2493. DOI: https://doi.org/10.1007/s11771-020-4474-z.

J. Cent. South Univ. (2020) 27: 2479-2493
DOI: https://doi.org/10.1007/s11771-020-4474-z

Kamyar TOLOUEI1, Ehsan MOOSAVI1, Amir Hossein BANGIAN TABRIZI1,Peyman AFZAL1, Abbas AGHAJANI BAZZAZI2
1. Department of Petroleum and Mining Engineering, South Tehran Branch, Islamic Azad University,Tehran, Iran;
2. Department of Mining Engineering, University of Kashan, Kashan, Iran
 Central South University Press and Springer-Verlag GmbH Germany,part of Springer Nature 2020
Central South University Press and Springer-Verlag GmbH Germany,part of Springer Nature 2020
Abstract: One of the surface mining methods is open-pit mining, by which a pit is dug to extract ore or waste downwards from the earth’s surface. In the mining industry, one of the most significant difficulties is long-term production scheduling (LTPS) of the open-pit mines. Deterministic and uncertainty-based approaches are identified as the main strategies, which have been widely used to cope with this problem. Within the last few years, many researchers have highly considered a new computational type, which is less costly, i.e., meta-heuristic methods, so as to solve the mine design and production scheduling problem. Although the optimality of the final solution cannot be guaranteed, they are able to produce sufficiently good solutions with relatively less computational costs. In the present paper, two hybrid models between augmented Lagrangian relaxation (ALR) and a particle swarm optimization (PSO) and ALR and bat algorithm (BA) are suggested so that the LTPS problem is solved under the condition of grade uncertainty. It is suggested to carry out the ALR method on the LTPS problem to improve its performance and accelerate the convergence. Moreover, the Lagrangian coefficients are updated by using PSO and BA. The presented models have been compared with the outcomes of the ALR-genetic algorithm, the ALR-traditional sub-gradient method, and the conventional method without using the Lagrangian approach. The results indicated that the ALR is considered a more efficient approach which can solve a large-scale problem and make a valid solution. Hence, it is more effectual than the conventional method. Furthermore, the time and cost of computation are diminished by the proposed hybrid strategies. The CPU time using the ALR-BA method is about 7.4% higher than the ALR-PSO approach.
Key words: open-pit mine; long-term production scheduling; grade uncertainty; augmented Lagrangian relaxation; particle swarm optimization algorithm; bat algorithm
Cite this article as: Kamyar TOLOUEI, Ehsan MOOSAVI, Amir Hossein BANGIAN TABRIZI, Peyman AFZAL, Abbas AGHAJANI BAZZAZI. Improving performance of open-pit mine production scheduling problem under grade uncertainty by hybrid algorithms [J]. Journal of Central South University, 2020, 27(9): 2479-2493. DOI: https://doi.org/10.1007/s11771-020-4474-z.
1 Introduction
The open pit mine is actually a superficial mining starting with the extraction of ore or waste from the surface by dint of digging the cavity. The mining operation is ended when the process develops with deeper and deeper caverns. Another foremost step in mining planning is long-term production scheduling (LTPS) optimization process. LTPS is especially important in mining projects, because in addition to determining the actual value of the project, medium-term and short-term schedules are planned based on it. Therefore, in the last decade, special attention has been paid to LTPS, providing optimal algorithms to obtain the best schedules by mining engineers. So far, two categories of deterministic algorithms and uncertainty-based algorithms for long-term schedules have been developed. In deterministic algorithms, all input data to the mathematical model of production scheduling are assumed to be definite, and uncertainty is not considered in these parameters. Thus, the operational constraints and different expectations of the mine cannot be met when operating in the mine.
The main reason for this inefficiency is the uncertainty of the tonnage and grade of the mineral. In uncertainty-based algorithms, the uncertainty of the input parameters is considered in the production scheduling model. LTPS is planned to extract and process the mineral for a period of more than 10 years. The main purpose of LTPS is to prepare annual and multi-year development schedules for all blocks in the mine-life. In fact, the goals of LTPS are to maximize the project’s net present value (NPV), minimize the risk of achieving production targets, and maximize mining life.
The LTPS problem is regarded as a hard integer programming problem and non- deterministic polynomial-time (NP) classes. It is difficult to achieve a suitable solution for the LTPS problem for the sake of its size and NP-hardness. Hence, several research efforts emphasize the efficient LTPS algorithms in order to proliferate profitability and diminish computational time. Table 1 illustrates a number of models presented in recent years.
Table 1 Review of presented models since 1969

Continued

Despite researchers’efforts, the LTPS problem has not been a well-solved problem. Most of the proposed models have disadvantages such as not considering the sources of uncertainty, not meeting operational constraints, generating non-optimal solutions in high computational time. With methodological and technological advances, researchers have the chance to challenge traditional approaches for computational reasons. This will lead to the development of new models with significant features that can enhance the capabilities of current solutions. The augmented Lagrangian relaxation method is efficiently used to solve constrained optimization problems [51-53]. It mostly exploits the specific decomposable structure of the initial problem to deal with large-scale hard problems in different fields, such as production scheduling optimization problems. To determine the multiplier values relying on the previous computation consequences, the authors apply the sub-gradient (SG) method that is generally utilized. According to the zigzag phenomenon and small steps, the sub-gradient procedure may join gradually on large problems. The use of this method has been increased in recent years by incorporating meta-heuristic algorithms. They can be simply used for the solution of hard optimization problems and they are responsible for great modeling flexibility. The results in different industries demonstrate the high efficiency of this model. Particle swarm optimization (PSO) and bat algorithm (BA) are among the most widely used meta-heuristic algorithms that have features such as rapid convergence and the production of optimal solutions in a logical time for solving various optimization problems [54-56].
The present paper scrutinizes the use of meta-heuristic methods in solving the long-term production scheduling optimization problem in deterministic and uncertainty conditions. To solve the LTPS problem under grade uncertainty condition, we introduce two hybrid models between the augmented Lagrangian relaxation (ALR) method and the particle swarm optimization (PSO) algorithm and similarly between ALR and bat algorithm (BA). In this research, it is suggested to enhance the convergence rate by the ALR method on the LTPS problem. Furthermore, also the PSO and BA are practiced to bring up to date Lagrange coefficients. The presented models have been compared with the outcomes of combining ALR with genetic algorithm (GA), traditional sub- gradient method (SG), and the conventional method without using the Lagrangian approach (Conv.). In terms of average net present value, average ore grade, and CPU time, results illustrate that ALR-BA generates the best outcomes while satisfying constraints. The results indicate that the advanced versions have significantly improved in comparison with the conventional method.
The next part of this paper is provided as below. According to the condition of grade uncertainty, the objective functions and their associated restrictions are modeled in Sections 2 and 3. A summary of the methodology and hybrid models is divulged in Sections 4 to 7 and the proposed models will be also advanced. Next, an assessment of the results is displayed in Section 8. Moreover, this section includes data collection and preparation. Authentication of the recognized models is realized. Finally, Section 9 carries out the conclusion.
2 Traditional formulation of LTPS problem
Long-term production scheduling model has been practiced to project production aims and ore material current over several years. Holistically, it takes a basic image of the production and expressed as a linear problem.
2.1 Objective function
To reflect decision-making determinations, the simplest way is to signify a complete space optimization model for each period of the scheduling horizon. Since the obtainability of restrains is intermingled into the model, the LTPS problem is contributed:

In the constructed model, the following indications were recognized: n is the block identification number, n=1, 2, …, N; N is the total number of blocks to be scheduled; t is the scheduling periods index, t=1, 2, …, T; T is the total number of scheduling periods;  is the net value to be generated by mining block n in period t; r is the discount rate in each period;
is the net value to be generated by mining block n in period t; r is the discount rate in each period;  is the binary variable as follows:
is the binary variable as follows:
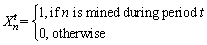
2.2 Constraints
Constraints are based on Ref. [16] as follows.
2.2.1 Grade blending constraints
In the production scheduling, one of the most substantial complications is the ore grade which has to be put to one side steady while directing to the processing plant. Henceforth, the grade of ore that is being directed to the mill has to definite between two limits.
1) Upper bound constraints: It is worth mentioning that the average grade of the material led to the mill should be a slighter quantity or equivalent to the certain grade value, Gmax, for each period, t:

where gn is the average grade of block n and On is the ore tonnage in block n.
2) Lower bound constraints: Notably, the average grade of the material directed to the mill should be more or the same as the fixed value, Gmax, for each period, t:

2.2.2 Reserve constraints
Basically, restrictions are affected for each block so as to specify that all measured blocks in the model cannot be mined more than once.

2.2.3 Processing capacity constraint
Total tons of the treated ore should be less than the processing capacity, PCmax, in every period, t:

2.2.4 Mining capacity constraint
The whole available mining capacity, MCmax, should be more than the whole quantity of material (waste and ore) to be mined for each period, t:

where Wn is the tonnage of waste material within block n.
2.2.5 Slope constraints
These constraints verify that before mining a specified block, all of the overlying blocks should be mined. The following two methods are applied to implement these constraints:
1) Using one constraint for each block per period:

where k is the index of a block considered extraction at period t; Y is the total number of blocks overlying block k; y is the counter for the Y-overlying blocks.
2) Using Y-constraints for each block at each period:

3 LTPS model considering grade uncertainty
3.1 Importance of uncertainty in LTPS
In engineering projects, various sources of uncertainty complicate decisions. Principally, the risks associated with a project arise from the uncertainties in that project, which can affect goals. Due to the importance of this subject, the classification of uncertainty sources in mining projects was provided by DIMITRAKOPOULOS [57]:
1) The uncertainty of the grade and the uncertainty of tonnage bring about the uncertainty of the ore deposit model.
2) Technical uncertainty, such as extraction, reveals slope constraints, drilling capacity, etc. Economic uncertainties include capital costs, operating costs, and product prices.
3) Among the uncertainties, grade uncertainty directs into a large share of probabilities.
3.2 LTPS model via grade uncertainty
The indicator kriging (IK) is one of the applied procedure methods for grade estimation in mining projects. This method was proposed by JOURNEL [58] to estimate the resources. The indicator method is binary data encoding related to the cut-off value, Zc. For the Z(x), ik(x)=1, if Z(x)≥Zc, and otherwise, ik(x)=0. In fact, it is a nonlinear conversion of data to the binary systems. Values between 0 and 1 for each estimation point provide a set of indicators- converted quantity using kriging that can be expounded as the proportion of the block overhead the determined cut-off on data support and the probability that the grade is overhead the determined indicator [25]. In the optimization process of this study, this probability is contemplated as the probability index (PIn) for block n. The high probability blocks have less risk than low probability ones.
Actually, in the current section, an integer programming-based model with considering grade uncertainty has been developed. In this method, a weight based on indicator kriging is assigned to each block (PIn), which indicates the probability made from n for each block in the block model. This approach establishes the objective function in such a way that the initial production periods are allocated to the higher-certainty mineral blocks. Subsequently, the other objective function is presented to the objective function of the traditional model as follows:

This objective function is subject to the constraints (2) to (8).
4 ALR function for LTPS problem
Now, the ALR method is measured as one of the possible methods for making out the projected problem.
4.1 LR scheme
The Lagrangian relaxation (LR) method is recognized as one of mathematical means for a mixed-integer programming problem. In the presentation [59-63] of this technique in LTPS, system limitations are relaxed by Lagrangian multipliers and presented to the objective function. Next, the relaxed problem is rankled into a more practicable sub-problem for distinct units and solved via dynamic programming. Due to the violations of system restraints, the coefficients are promoted by dint of a sub-gradient method. The convergence standard is achieved if the duality gap is within a certain limit.
LR relaxes the system constraints as a result of Lagrangian multipliers. Then the relaxed problem is split into some smaller sub-problems. The constant Lagrangian function can be made by dint of assigning non-negative Lagrangian multipliers λt, μt and Vt in terms of processing type at period t to the constraints. The LTPS problem is illuminated through the Lagrangian relaxation method by relaxing or momentarily ignoring the preventing constraints and solving the problem as if they have never been. While maximizing due to the control variable  in the LTPS problem, this is done over the dual optimization process, which strives to affect the constrained optimum by lessening the Lagrangian function L due to the Lagrangian multipliers λt, μt and Vt:
in the LTPS problem, this is done over the dual optimization process, which strives to affect the constrained optimum by lessening the Lagrangian function L due to the Lagrangian multipliers λt, μt and Vt:
j*=Min j(λ, μ, V), where j(λ, μ, V)=Max L(X, λ, μ, V).
λ, μ, V X
4.2 ALR scheme
For the time being, the ALR method is identified as one of the possible methods for solving the proposed problem. Considering the augmented Lagrangian function proposed by ANDREANI et al [64], an ALR technique is practiced, which can efficiently produce viable solution for the main problem. For the following constrained optimization problem, assume f, g, h to admit continuous first derivatives as follows:
Minf(x)
s.t. h(x)=0, g(x)≤0, x∈Ω={x|H(x)=0, G(x)≤0}.
Consider the following augmented Lagrangian function as:

4.3 ALR for LTPS problem reformulation
When the coupling constraints (4)-(6) are relaxed, the above reformulation contributes to decomposing the resulted model (9) into a number of sub-problems. To solve the open pit mines LTPS problem, the augmented Lagrangian relaxation method is employed in the present paper.
The novel maximization objective is alike to the minimization of a reviewed objective function. At this point, the objective is specified as:

Explicitly, equality and inequality constraints (4)-(6) are relaxed and the subsequent augmented Lagrangian relaxation problem is acquired:

According to the objective function, we have:

The adjustment of Lagrangian multipliers should be carefully completed so as to curtail the Lagrangian function based on the Lagrangian multipliers. To reach a quick solution, a combination of sub-gradient method and various meta-heuristics are needed to be used by most references to adjust Lagrangian multipliers to alter Lagrangian multipliers. In this research, the Lagrangian multipliers are adjusted and the performance of augmented Lagrangian relaxation method is improved through using the particle swarm optimization (PSO) algorithm and bat algorithm (BA).
5 PSO methodology
In 1995, the PSO methodology was first introduced by EBERHART et al [65] and KENNEDY et al [66]. This was an optimization method based on probability rules. Researchers have pondered the social behavior of bird or fish groups while searching for food so that the population can be guided to a promising area for space search. Certain sensible processes are practiced for the manners of the creatures of the ruling body. Birds modify their physical movements by escaping missions to search for food. Hence, every one of the group member supposedly uses the previous experiences and other detections from members in order to find food. This kind of corporation is considered a positive movement within a competitive search for food. The PSO is grounded on the idea of sharing information among the group members. In PSO, a particle is denoted to each answer to a problem which is the situation of a bird in the search space. All particles include a degree of ability that the quality of action optimizes it. Furthermore, each particle embraces a factor called velocity which identifies it in the search range [67-69].
The PSO starts with a group of inadvertent replies. Next, it searches for the location and velocity of each particle so as to determine the best answer in the problem space. The two most remarkable values indicate that each particle is identified at each step of population movement.
As a result, the first step is recognized as the finest answer in terms of suitability ever obtained for each particle. This is actually the personal best and is termed pbest. The global best, identified as gbest, is another best value ever attained by means of the PSO. To search for new solutions, swarm of particles is randomly initialized over the searching space and moves through D-dimensional space. Authorize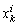 and
and  respectively to be the position and velocity of the i-th particle in the searching space at the k-th iteration, then its velocity and position of this particle at the (k+1)th iteration are updated using the following equations:
respectively to be the position and velocity of the i-th particle in the searching space at the k-th iteration, then its velocity and position of this particle at the (k+1)th iteration are updated using the following equations:
 (14)
(14)
 (15)
(15)
where r1 and r2 demonstrate accidental numbers between 0 and 1, respectively; c1 and c2 are constants;  demonstrates the best position of the i-th particle, and
demonstrates the best position of the i-th particle, and  correlates with the global best position in the swarm up to the kth iteration. The PSO algorithm pseudocode is shown in Figure 1.
correlates with the global best position in the swarm up to the kth iteration. The PSO algorithm pseudocode is shown in Figure 1.

Figure 1 Pseudocode of PSO algorithm
6 Bat algorithm
Group-behavior-based collective intelligence is one of the most robust optimization techniques. YANG [70] proposed an algorithm inspired by the collective behavior of bats within a natural environment predicated on the reception of reflected sound by bats. They can track the exact direction and location of their prey by the pulse-echo technique (sending soundwaves and receiving their reflection). They can also draw a sound image of barriers that connect their loci and identify them well when soundwaves return to the bat wave sender. This system enables bats to detect mobile objects like trees and insects. Microbats are constantly sending short-lived loud beats of sound in the range of 25-150 kHz and listening to the echo that rebounds from nearby objects to catch prey or evade obstacles. They naturally emit 10-20 pulses per second (PPS) and can increase it to approximately 200 PPS as they get closer to their target. YANG [70] provided the following paths for transferring these specific characteristics of bats to an optimization algorithm:
1) All bats rehearse their echolocation capability in determining how distant they are from a particular object and somehow they differentiate between food (prey) and the background barrier. They all really benefit from echolocation abilities.
2) Bats can modify loudness A0 and wavelengths λ of emitted sound pulses to find food; therefore, they can fly unwittingly at velocity Vi in position xi at frequency fmin. They can also change wavelengths and rate or frequency of their issued pulse as per the distance that they have with their prey.
3) Loudness fluctuates between a big positive value A0 and the lowest constant value Amin.
The current position of each bat is considered to be a feasible solution to the optimization problem [71-73].
Pursuant to regulation, velocity and position
and position  for each i-th virtual bat in the t-th iteration and frequency fi can be measured as follows:
for each i-th virtual bat in the t-th iteration and frequency fi can be measured as follows:
 (16)
(16)
 (17)
(17)
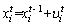 (18)
(18)
In the equation above,  represents a uniformly distributed random vector and x* is the current optimal position, chosen in each iteration after being compared with the position of the virtual bats. Frequency f is typically considered to be fmin= 0 and fmax=100. In each iteration, a solution in local search is selected as the optimal solution, and the new position of each bat is locally updated with random steps:
represents a uniformly distributed random vector and x* is the current optimal position, chosen in each iteration after being compared with the position of the virtual bats. Frequency f is typically considered to be fmin= 0 and fmax=100. In each iteration, a solution in local search is selected as the optimal solution, and the new position of each bat is locally updated with random steps:
xnew=xold+∈ (19)
(19)
In the equation above, ∈∈[-1, 1] denotes a random number and  denotes the mean loudness of the bats in the t-th iteration. Furthermore, loudness Ai and pulse rate r that is transmitted every time are updated as follows:
denotes the mean loudness of the bats in the t-th iteration. Furthermore, loudness Ai and pulse rate r that is transmitted every time are updated as follows:
 (20)
(20)
 =r0i[1-exp(-γt)] (21)
=r0i[1-exp(-γt)] (21)
In the above equation, α and γ are constants and r>0 and 0<α<1. When t→∞, we have  and
and  Figure 2 depicts the pseudocode of the bat algorithm.
Figure 2 depicts the pseudocode of the bat algorithm.

Figure 2 Pseudocode of bat algorithm
7 Framework of proposed models
In the present research, two steps are required for the hybrid methods. The first one states the Lagrangian function which brings up-to-date the Lagrange multipliers. The second step is the precise global extension of the stated ALR function, in which the PSO, BA and GA are utilized to find out a new stochastic method near to the ideal maximum. Figure 3 shows the flowchart of the suggested approach.

Figure 3 Flowchart of proposed models
8 Numerical results
The presented model was expanded, executed, and assessed in MATLAB R2019a environment. The proposed experiment has been executed on an Intel Quad-Core, 3.5 GHz, and 32 GB RAM PC and MS Windows 7. All the developed formulations are tested on the numerical experiments on the artificial data set including 2150 blocks. In conclusion, the enactment by ALR-BA is actually better than other methods from the view of the duality gap (Table 2).
The duality gap will be applied to evaluate the modality of the solutions generated by the meta-heuristic algorithms. The duality gap among the best solutions produced by the various kinds of the meta-heuristic algorithms, i.e., Zapprox and the optimal solution found by MATLAB, i.e., ZMATLAB is computed using the following equation:
 (22)
(22)
To compare the suggested mathematical model for LTPS, the push-back data of an iron ore of central Iranian iron ore body are selected as a case study. The presented model was implemented in the CHADORMALU mine. Also, its deposit has been recogniszed as the major iron ore one in the central part of Iran. CHADORMALU is located at the center of PERSIA (IRAN) Desert, at the north of grey CHAH-MOHAMMAD Mountains. 400 million tons of resource and 320 million tons of reserves are divided between northern and southern ore bodies by averaged Fe- and P-content of 55.2%, 0.9%, respectively.
Table 2 Numerical results for synthetic data set containing 2150 blocks

Four push-backs are scheduled for the CHADORMALU mine. The mathematical model presented in this paper is practiced in the second push-back. The 3D view of the second push-back is illustrated in Figure 4. This push-back includes 6854 blocks of which 2754 are ore blocks and 4100 are waste blocks. The tonnage of waste and ore presented in the aforementioned push-back shall be 103.8 and 110.2 million tons, respectively (with a waste ratio of 0.94). The technical and economic parameters and also, the number of model variables for the second push-back of CHADORMALU mine are illustrated in Tables 3 and 4.
Figures 5 and 6 show the numerical results of the proposed model for the CHADORMALU push-back data set including 12 planning periods with deterministic assumption and considering grade uncertainty. The comparison of the average net present value of the total of 12 years for all presented models in deterministic and uncertainty- based conditions is shown in Figure 7. As disclosed in Figure 7, with considering grade uncertainty, the average net present value using the ALR–BA method is 4.056 M$ and the average net present values through the ALR-PSO, ALR-GA, ALR-SG, BA, PSO, GA, SG, and conventional methods are 3.996, 3.787, 3.741, 3.947, 3.914, 3.681, 3.589 and 3.527 M$, respectively.

Figure 4 A 3D view of second push-back in CHADORMALU mine [25]
Table 3 Technical and economic parameters

Table 4 Number of model variables for second push-back of CHADORMALU mine


Figure 5 Comparison of NPV for CHADORMALU mine obtained by presented models in deterministic condition

Figure 6 Comparison of NPV for CHADORMALU mine obtained by presented models with considering grade uncertainty

Figure 7 Comparison of average NPV in total 12 years obtained by presented models in deterministic and uncertainty-based conditions
Additionally, the average grades of the ore for the case study in deterministic and uncertainty- based conditions are displayed in Figures 8 and 9. Also, the comparison of the average ore grade of the total of 12 years for all presented models with assumed deterministic condition and concerning with grade uncertainty is demonstrated in Figure 10. In uncertainty-based condition, the average grade of ore in the total of 12 years by the ALR–BA method is 54.84% and for the ALR-PSO, ALR-GA, ALR-SG, BA, PSO, GA, SG, and conventional methods are 54.71%, 54.03%, 53.90%, 54.56%, 54.45%, 53.75%, 53.58% and 53.49%, respectively.
The ore productions from the assessed methods, in conditions of deterministic and uncertainty, are shown in Figures 11 and 12. According to the obtained results, the suggested method (ALR-BA), while satisfying the constraints of mining capacity and processing capacity, generates the best outcomes in comparison with other methods.

Figure 8 Comparison of average grade of ore for CHADORMALU mine obtained by presented models in deterministic condition
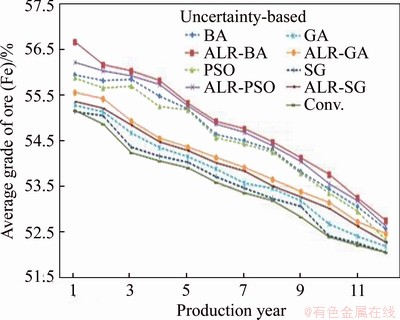
Figure 9 Comparison of average grade of ore for CHADORMALU mine obtained by presented models with considering grade uncertainty

Figure 10 Comparison of average grade of ore in total 12 years obtained by presented models in deterministic and uncertainty-based conditions

Figure 11 Ore production obtained by presented models in deterministic condition

Figure 12 Ore production obtained by presented models in uncertainty-based condition
Furthermore, Table 5 shows the CPU time and the duality gap of each method. The results show that the suggested method (ALR-BA) has the lowest CPU time and duality gap compared to other methods, and its CPU time is about 7.4% better than ALR-PSO. The difference in the results indicates the capability of the proposed method and the weakness of the previous methods.
Table 5 General information about solution found by MATLAB for proposed models

9 Conclusions
The aim of this research is to present a mathematical model for long-term production planning and achieve the highest revenue in the grade uncertainty situation. To make the long-term production planning, grade uncertainty was applied as an input feature to the mathematical model of production planning. A long-term production development optimization model grade uncertainty is employed as the binary integer programming.
Principally, the possibility index for each block of ore was determined to point out the grade uncertainty. For the next step, getting the best out of the net present value with physical and operational constraints was practiced to model the objective function. Blocks with higher probabilities have less risk than the blocks with lower probability. The proposed model has considered grade uncertainty in the mining sequence. The present paper suggested the hybrid method of the augmented Lagrangian relaxation-bat algorithm in order to solve the long-term production problem in open-pit mines as it is hard to solve the production planning models in the open-pit mines. This research also presented a new approach due to the optimization of Lagrange coefficients and comparing its performance with the traditional SG method in the Lagrangian relaxation method.
The results of the case study prove that the augmented Lagrangian relaxation method can carry out a suitable solution to the main problem. The hybrid strategy can produce a more effective solution to the near-optimal solution in comparison with the conventional method. Moreover, it was specified that the stable convergence property and prevention of early convergence are identified as the main advantages of the method suggested in this research. In terms of average net present value, average ore grade and CPU time, results illustrate that ALR-BA generates the best outcomes while satisfying constraints. The CPU time by the ALR-BA hybrid method was 201.73 min less than the conventional method and also was 2.18, 5.85, 8.70, 51.67, 59.81, 61.95 and 83.11 min less than the ALR-PSO, ALR-GA, ALR-SG, BA, PSO, GA, and SG procedures, respectively.
Contributors
The main research targets were expanded by Ehsan MOOSAVI and Kamyar TOLOUEI. Kamyar TOLOUEI and Ehsan MOOSAVI conducted the literature review and wrote the first draft of the manuscript. Ehsan MOOSAVi and Kamyar TOLOUEI established the models and calculated the results. Amir Hossein BANGIAN TABRIZI, Peyman AFZAL and Abbas AGHAJANI BAZZAZI analyzed the calculated results and edited the draft of manuscript. All authors replied to reviewers & apos; comments and revised the final version.
Conflict of interest
Kamyar TOLOUEI, Ehsan MOOSAVI, Amir Hossein BANGIAN TABRIZI, Peyman AFZAL, Abbas AGHAJANI BAZZAZI declare that they have no conflict of interest.
References
[1] JOHNSON T B. Optimum production scheduling [C]// Proceedings of 8th International Symposium on Computers and Operations research. Salt Lake City, 1969: 539-562.
[2] WILLIAMS C E. Computerized year-by-year open pit mine scheduling [J]. Society of Mining Engineers, AIME, Transactions, 1974, 256: 45-52.
[3] GERSHON M E. Optimal mine production scheduling: evaluation of large scale mathematical programming approaches [J]. International Journal of Mining Engineering, 1983, 1(4): 315-329.
[4] DAGDELEN K, JOHNSON T B. Optimum open pit mine production scheduling by Lagrangian parametrization [C]// Proceeding of the 19th International Symposium on the Application of Computers and Operations Research in the Mineral Industry. Pennsylvania, University Park: Pennsylvania State University, 1986, 13: 127-142.
[5] RAVENSCROFT P J. Risk analysis for mine planning by conditional simulation [J]. Transactions of the Institution of Mining and Metallurgy, Section A: Mining Technology, 1992, 101: 82-88.
[6] DOWD P A. Risk assessment in reserve estimation and open-pit planning [J]. Transactions of the Institution of Mining and Metallurgy, Section A: Mining Technology, 1994, 103: 148-154.
[7] ELEVLI B. Open pit mine design and extraction sequencing by use of OR and AI concept [J]. International Journal of Surface Mining, Reclamation and Environmental, 1995, 9: 149-153.
[8] DENBY B, SCHOFIELD D. Inclusion of risk assessment in open-pit design and planning [J]. Transactions of the Institution of Mining and Metallurgy, Section A: Mining Technology, 1995, 104: 67-71.
[9] TOLWINSKI B. Scheduling production for open-pit mines [C]// Proceedings of APCOM’98. 1994: 19-23.
[10] AKAIKE A, DAGDELEN K. A strategic production scheduling method for an open-pit mine [C]// Proceedings of the 28th Application of Computers and Operation Research in the Mineral Industry. 1999: 729-738.
[11] WHITTLE D. Proteus environment: Sensitivity analysis made easy [C]// Whittle North American Strategic Mine Planning Conference. Colorado, 2000.
[12] JOHNSON T B, DAGDELEN K, RAMAZAN S. Open pit mine scheduling based on fundamental tree algorithm [C]// Proceeding of the 30th International Symposium on the Application of Computers and Operations Research in the Mineral Industry SME: Littleton. 2002: 147-159.
[13] DIMITRAKOPOULOS R, FARRELLY C T, GODOY M. Moving forward from traditional optimization: Grade uncertainty and risk effects in open pit design [J]. Transactions of the Institutions of Mining and Metallurgy, Section A: Mining Technology, 2002, 111: 82-88.
[14] GODOY M, DIMITRAKOPOULOS R. Managing risk and waste mining in long-term production scheduling of open-pit mines [J]. SME Transactions, 2004, 316: 43-50.
[15] DIMITRAKOPOULOS R, RAMAZAN S. Uncertainty based production scheduling in open pit mining [J]. SME Transactions, 2004, 316: 106-112.
[16] RAMAZAN S, DIMITRAKOPOULOS R. Recent application of operations research in open pit mining [J]. SME Transactions, 2004, 316: 73-78.
[17] RAMAZAN S, DIMITRAKOPOULOS R. Traditional and new MIP models for production planning with in-situ grade variability [J]. International Journal of Surface Mining, Reclamation and Environment, 2004, 18(2): 85-98.
[18] GHOLAMNEJAD J, OSANLOO M, KARIMI B. A chance-constrained programming approach for open pit long-term production scheduling in stochastic environments [J]. The Journal of the South African Institute of Mining and Metallurgy, 2006, 106: 105-114.
[19] GHOLAMNEJAD J, OSANLOO M. A chance constrained integer programming model for open pit long-term production planning [C]// Proceedings of the Sixteenth International Symposium on Mine Planning and Equipment Selection (MPES). 2007: 359-372.
[20] RAMAZAN S, DIMITRAKOPOULOS R. Stochastic optimization of long-term production scheduling for open pit mines with a new integer programming formulation, orebody modelling and strategic mine planning [C]// The Australasian Institute of Mining and Metallurgy, Spectrum Series. 2007, 14(2): 385-392.
[21] BOLAND N, DUMITRESCU I, FROYLAND G, GLEIXNER A M. LP-based disaggregation approaches to solving the open pit mining production scheduling problem with block processing selectivity [J]. Computers & Operations Research, 2009, 36(4): 1064-1089.
[22] BLEY A, BOLAND N, FRICKE C, FROYLAND G. A strengthened formulation and cutting planes for the open pit mine production scheduling problem [J]. Computers & Operations Research, 2010, 37(9): 1641-1647.
[23] KUMRAL M. Robust stochastic mine production scheduling [J]. Engineering Optimization, 2010, 42(6): 567-579.
[24] LAMGHARI A, DIMITRAKOPOULOS R. A diversified Tabu search approach for the open-pit mine production scheduling problem with metal uncertainty [J]. European Journal of Operational Research, 2012, 222(3): 642-652.
[25] GHOLAMNEJAD J, MOOSAVI E. A new mathematical programming model for long-term production scheduling considering geological uncertainty [J]. The Journal of the Southern African Institute of Mining and Metallurgy, 2012, 112(2): 77-81.
[26] NANJARI E L, GOLOSINSKI T S. Optimising open pit mine scheduling taking into consideration time value of money and mining restrictions [J]. International Journal of Mining, Reclamation and Environment, 2013, 27(3): 156-165.
[27] SATTARVAND J, NIEMANN-DELIUS C. A new metaheuristic algorithm for long-term open pit production planning [J]. Archives of Mining Sciences, 2013, 58(1): 107-118.
[28] GOODFELLOW R, DIMITRAKOPOULOS R. Algorithmic integration of geological uncertainty in push back designs for complex multi-process open pit mines [J]. Mining Technology, 2013, 122(2): 67-77.
[29] DIMITRAKOPOULOS R, JEWBALI A. Joint stochastic optimization of short and long term mine production planning: Method and application in a large operating gold mine [J]. IMM Transactions, Mining Technology, 2013, 122(2): 110-123.
[30] LEITE A, DIMITRAKOPOULOS R. Stochastic optimization of mine production scheduling with uncertain ore/metal/waste supply [J]. International Journal of Mining Science and Technology, 2014, 24(6): 755-762.
[31] MOOSAVI E, GHOLAMNEJAD J, ATAEE-POUR M, KHORRAM E. Improvement of Lagrangian relaxation performance for open pit mines constrained long-term production scheduling problem [J]. Journal of Central South University, 2014, 21: 2848-2856.
[32] MOOSAVI E, GHOLAMNEJAD J, ATAEE-POUR M, KHORRAM E. A hybrid augmented Lagrangian multiplier method for the open pit mines long-term production scheduling problem optimization [J]. Journal of Mining Science, 2014, 50: 1047-1060.
[33] KOUSHAVAND B, ASKARI-NASAB H, DEUTSCH C V. A linear programming model for long-term mine planning in the presence of grade uncertainty and a stockpile [J]. International Journal of Mining Science and Technology, 2014, 24: 451-459.
[34] ASAD M W A, DIMITRAKOPOULOS R, ELDERT J V. Stochastic production phase design for an open pit mining complex with multiple processing streams [J]. Engineering Optimization, 2014, 46(8): 1139-1152.
[35] LAMGHARI A, DIMITRAKOPOULOS R, FERLAND A J. A variable neighbourhood descent algorithm for the open-pit mine production scheduling problem with metal uncertainty [J]. Journal of the Operational Research Society, 2014, 65: 1305-1314.
[36] SHISHVAN M S, SATTARVAND J. Long term production planning of open pit mines by ant colony optimization [J]. European Journal of Operational Research, 2015, 240(3): 825-836.
[37] MOKHTARIAN M, SATTARVAND J. An imperialist competitive algorithm for solving the production scheduling problem in open pit mine [J]. International Journal of Mining and Geo-Engineering, 2016, 50(1): 131-143.
[38] MOKHTARIAN M, SATTARVAND J. Commodity price uncertainty propagation in open-pit mine production planning by Latin hypercube sampling method [J]. Journal of Mining & Environment, 2016, 7(2): 215-227.
[39] GOODFELLOW R, DIMITRAKOPOULOS R. Global optimization of open pit mining complexes with uncertainty [J]. Applied Soft Computing, 2016, 40: 292-304.
[40] LAMGHARI A, DIMITRAKOPOULOS R. Progressive hedging applied as a metaheuristic to schedule production in open-pit mines accounting for reserve uncertainty [J].European Journal of Operational Research, 2016, 253(3): 843-855.
[41] LAMGHARI A, DIMITRAKOPOULOS R. Network-flow based algorithms for scheduling production in multi- processor open-pit mines accounting for metal uncertainty [J].European Journal of Operational Research, 2016, 250(1): 273-290.
[42] BAKHTAVAR E, JAFARPOUR A, YOUSEFI S. Optimal production strategy of bimetallic deposits under technical and economic uncertainties using stochastic chance- constrained programming [J]. Journal of Mining & Environment, 2017, 8(3): 475-485.
[43] KHAN A. Long-term production scheduling of open pit mines using particle swarm and bat algorithms under grade uncertainty [J]. Journal of the Southern African Institute of Mining and Metallurgy, 2018, 118: 361-368.
[44] RAHIMI E, MOOSAVI E, SHIRINABADI R, GHOLINEJAD M. Optimized algorithm in mine production planning, mined material destination, and ultimate pit limit [J]. Journal of Central South University, 2018, 25(6): 1475-1488.
[45] TAHERNEJAD M M, ATAEI M, KHALOKAKAIE R. A practical approach to open-pit mine planning under price uncertainty using information gap decision theory [J]. Journal of Mining & Environment, 2018, 9(2): 527-537.
[46] JELVEZ E, MORALES N, NANCEL-PENARD P. Open-pit mine production scheduling: Improvements to MineLib library problems [C]// Proceedings of the 27th International Symposium on Mine Planning and Equipment Selection (MPES). 2018: 223-232.
[47] KHAN A, ASAD M W A. A mathematical programming model for optimal cut-off grade policy in open pit mining operations with multiple processing streams [J]. International Journal of Mining, Reclamation and Environment, 2020, 34(3): 149-158.
[48] ALIPOUR A, KHODAIARI A A, JAFARI A, TAVAKKOLI- MOGHADDAM R. Uncertain production scheduling optimization in open-pit mines and its ellipsoidal robust counterpart [J]. International Journal of Management Science and Engineering Management, 2018, 13(3): 225.
[49] CHATTERJEE S, DIMITRAKOPOULOS R. Production scheduling under uncertainty of an open-pit mine using Lagrangian relaxation and branch-and-cut algorithm [J]. International Journal of Mining, Reclamation and Environment, 2020, 34(5): 343-361.
[50] SENECAL R, DIMITRAKOPOULOS R. Long-term mine production scheduling with multiple processing destinations under mineral supply uncertainty, based on multi- neighbourhood Tabu search [J]. International Journal of Mining, Reclamation and Environment, 2020, 34(7): 459-475.
[51] DIEU V N, ONGSAKUL W. Augmented Lagrange hopfield network based Lagrangian relaxation for unit commitment [J]. Electrical Power and Energy Systems, 2011, 33: 522-530.
[52] TOSSERAMS S, ETMAN L F P, PAPALAMBROS P Y, ROODA J E. An augmented Lagrangian relaxation for analytical target cascading using the alternating direction method of multipliers [J]. Structural and Multidisciplinary Optimization, 2006, 31: 176-189.
[53] RODRIGUES R N, da SILVA E L, FINARDI E C, TAKIGAWA F Y K T. Solving the short-term scheduling problem of hydrothermal systems via lagrangian relaxation and augmented Lagrangian [J]. Mathematical Problems in Engineering, 2012: 856178.
[54] XU H A, BAO Z R A, ZHANG T. Solving dual flexible job-shop scheduling problem using a Bat algorithm [J]. Advances in Production Engineering & Management, 2017, 12 (1): 5-16.
[55] SUNDARAM A, PAULO’S FORSIDO A, GERMAMO K M. Unit commitment using meta-heuristic search algorithm [J]. Imperial Journal of Interdisciplinary Research (IJIR), 2016, 2(12): 5-10.
[56] ZHU B, ZHU W, LIU Z, DUAN Q, CAO L. A novel quantum-behaved bat algorithm with mean best position directed for numerical optimization [J]. Computational Intelligence and Neuroscience, 2016, Article ID 6097484.
[57] DIMITRAKOPOULOS R. Conditional simulation algorithms orebody uncertainty in open pit optimization [J]. International Journal of Surface Mining Reclamation and Environment, 1998, 12: 173-179.
[58] JOURNEL A G. Non-parametric estimation of spatial distributions [J]. MathematicalGeosciences, 1983, 15(3): 445-468.
[59] COHEN A I, WAN S H. A method for solving the fuel constrained unit commitment problem [J]. IEEE Transactions on Power Systems, 1987, 2: 608-614.
[60] VEMURI S, LEMONIDIS L. Fuel constrained unit commitment [J]. IEEE Transactions on Power Systems, 1992, 7(1): 410-415.
[61] ABDUL-RAHMAN K H, SHAHIDEHPOUR S M, AGANAGIC M, MOKHTARI S. A practical resource scheduling with OPF constraints [J]. IEEE Transactions on Power Systems, 1996, 11(1): 254-259.
[62] PANG Xin-fu, GAO Liang, PAN Quan-ke, TIAN Wei-hua, YU Sheng-ping. A novel Lagrangian relaxation level approach for scheduling steelmaking-refining-continuous casting production [J]. Journal of Central South University, 2017, 24(2): 467-477.
[63] FISHER M L. The Lagrangian relaxation method for solving integer programming problems [J]. Management Science Journal, 1981, 27(1): 1-18.
[64] ANDREANI R, BIRGIN E G, MARTINEZ J M, SCHUVERDT M L. On augmented Lagrangian methods with general lower-level constraints [J]. SIAM Journal on Optimization, 2008, 18(4): 1286-1309.
[65] EBERHART R, KENNEDY J. A new optimizer using particle swarm theory [C]// Proceedings of the Sixth International Symposium on Micro Machine and Human Science. IEEE Service Center, 1995: 39-43.
[66] KENNEDY J, EBERHART R. Particle swarm optimization [C]// IEEE International Conference on Neural Networks 1995 (ICANN’95). Perth, Australia, 1995, 5: 1942-1948.
[67] van DEN BERGH F, ENGELBRECHT A P. A new locally convergent particle swarm optimizer [C]// IEEE Conferences on Systems, 2002.
[68] CHUNMING Y, SIMON D. A new particle swarm optimization technique [C]// 18th International Conferences System Engineering (ICSEng). 2005, 2: 164-169.
[69] KENNEDY J, EBERHART R. A discrete binary version of the particle swarm algorithm [C]// IEEE International Conference on Computational Cybernetics and Simulation. 1997, 5: 4104-4108.
[70] YANG X S. A new metaheuristic bat-inspired algorithm [C]// Proceedings of Nature Inspired Cooperative Strategies for Optimization (NICSO 2010), Studies in Computational Intelligence Series. Springer, Berlin/Heidelberg, 2010, 284: 65-74.
[71] MIRJALILI S A, MIRJALILI S M, YANG X S. Binary bat algorithm [J]. Neural Computing and Applications, 2014, 25(3, 4): 663-681.
[72] YANG X S, HE X. Bat algorithm: Literature review and applications [J]. International Journal of Bio-Inspired Computation, 2013, 5(3): 141-149.
[73] YANG X S. Bat algorithm for multi-objective optimization [J]. International Journal of Bio-Inspired Computation, 2011, 3(5): 267-274.
(Edited by YANG Hua)
中文导读
混合算法改善品位不确定露天矿生产调度问题的性能
摘要:露天采矿工艺是地表采矿的一种方法,通过开挖坑洞从地表向下开采矿石或废物。工业生产过程中,露天矿的长期生产调度(LTPS)问题是最大的生产难题之一,而基于确定性方法和不确定性的方法被认为是解决此类问题的主要策略。在过去几年中,许多研究人员充分探究了一种成本较低的新型计算法,即元启发式方法,用以解决矿山设计和生产调度问题。该方法尽管无法保证最终方案的最优性,但能够以相对较低的计算成本推算出足够优秀的解决方案。本文提出了增强拉格朗日松弛(ALR)与粒子群优化(PSO),以及ALR和蝙蝠算法(BA)的两种混合算法模型,以解决不确定品位条件下的露天矿生产调度问题。该混合模型采用ALR方法解决露天矿生产调度问题,以提高其计算性能并加快收敛速度,并通过PSO或BA更新拉格朗日系数。所提出的计算模型与ALR遗传算法、ALR传统次梯度法和常规方法(未使用拉格朗日方法)的计算结果进行了比较,结果表明:相比于常规方法,ALR法可以更加有效地解决大规模问题,并提出合理的解决方案。此外,混合算法可以降低计算时间和成本,ALR-BA方法的CPU运算时间比ALR-PSO方法大约高7.4%。
关键词:露天矿;长期生产调度;品位不确定性;拉格朗日松弛;粒子群算法
Received date: 2019-11-28; Accepted date: 2020-07-02
Corresponding author: Ehsan MOOSAVI, PhD, Assistant Professor; Tel: +98-9138375368; E-mail: se.moosavi@yahoo.com, se_moosavi@azad.ac.ir; ORCID: https://orcid.org/0000-0002-5626-2689

