
DOI: 10.11817/j.issn.1672-7207.2019.11.023
干湿循环下受弯钢筋混凝土梁的氯盐侵蚀
蔡健1, 2,李名铠1,陈庆军1, 2,赖骏1,魏沐杨1
(1. 华南理工大学 土木与交通学院,广东 广州,510641;
2. 亚热带建筑科学国家重点实验室,广东 广州, 510641)
摘要:为探究弯曲荷载对干湿交替环境下钢筋混凝土梁内氯离子输运的影响,引入混凝土标量损伤作为耦合中间量,并拟合氯离子的荷载修正函数修正不同损伤部位的氯离子扩散系数,建立干湿循环与弯曲荷载耦合作用下混凝土梁中的氯盐和水分的输运模型。在此基础上,基于COMSOL软件,提出一种混凝土中氯盐侵蚀的数值模拟方法,并以弯曲荷载、侵蚀时间为变量,进行干湿循环试验验证。研究结果表明:随着弯曲荷载、侵蚀时间增加,混凝土梁内同一位置处的氯离子质量分数提高;对于同一试验梁,纯弯段氯离子质量分数比弯剪段的高;弯曲荷载影响构件的损伤范围和程度,进而影响氯离子在混凝土内的传输。
关键词:干湿循环;氯盐侵蚀;弯曲荷载;混凝土损伤;数值模拟
中图分类号:TU528.1 文献标志码:A 开放科学(资源服务)标识码(OSID)
文章编号:1672-7207(2019)11-2840-11
Chloride ingression in reinforced concrete beams subjected to flexural loading under cyclic drying-wetting condition
CAI Jian1, 2, LI Mingkai1, CHEN Qingjun1, 2, LAI Jun1, WEI Muyang1
(1. School of Civil Engineering and Transportation, South China University of Technology,Guangzhou 510641, China;
2. State Key Laboratory of Subtropical Building Science, Guangzhou 510641, China)
Abstract: In order to explore the impact of flexural loading on chloride ion transport in reinforced concrete beam under cyclic drying-wetting condition, a concrete scalar damage was introduced as the coupling intermediate quantity, and a well-fitted load correction function was presented to correct the chloride diffusion coefficient of different damage parts. Transportation model of chloride ion and water in concrete beams was established by considering the coupling effect of drying-wetting cycles and flexural loading. On this basis, a numerical analysis method was proposed using COMSOL to simulate the chloride ingression. Experimental investigation was carried out on reinforced concrete beams with flexural loading and ingression duration as variables. The results show that the chloride ion mass fraction at specific position in concrete beams increases with the increase of flexural loading and ingression duration. The chloride ion mass fraction is relatively higher in bending section than that of bending shear section for each test beam. Flexural loading affects the damage range and degree of elements, which further affects the transportation of chloride ion.
Key words: cyclic drying-wetting; chloride ingression; flexural loading; concrete damage; numerical simulation
临海混凝土结构根据所处的环境可分为不同的结构分区。其中,干湿交替区域的混凝土在对流和扩散的共同作用下,氯离子以较快速度渗透至混凝土内部,因此,该区域是结构耐久性设计的关键部位。混凝土结构在服役过程中的受荷状态会对氯离子的输运产生影响,而弯曲荷载则是结构构件服役过程中最常见的荷载类型之一。因此,对干湿环境下受弯混凝土构件的氯盐侵蚀机理进行研究,提出易用的计算方法,对其耐久性设计及寿命预测具有重要意义。对于干湿交替区域的氯盐侵蚀,采用传统的菲克第二定律拟合检测数据存在一定的误差。因此,国内外学者对非饱和状态下混凝土中氯盐侵蚀机理展开了广泛研究。ABABNEH等[1-2]建立了非饱和状态下混凝土中氯离子传输模型。改进后的模型较为复杂,一般无法直接求解,部分学者尝试采用差分方法进行解答,并通过试验进行验证[2-4]。此外,在荷载作用下,混凝土中出现微观和宏观裂缝,改变氯离子的侵蚀速度。YE等[5]对钢筋混凝土梁施加弯曲荷载并进行干湿循环试验,发现低压应力对氯离子侵蚀有阻碍作用,高压应力和拉应力有促进氯离子侵蚀的作用;并以混凝土应力和峰值应力的比值为变量提出了幂函数形式氯离子扩散系数的荷载影响公式。WANG等[6-7]基于试验提出以荷载比为变量的氯离子扩散系数修正系数。陆春华等[8]针对受弯开裂混凝土,提出考虑裂缝效应的“等效氯离子扩散系数”来进行简化分析。蔡健等[9-10]在饱和状态下钢筋混凝土、非饱和状态下的预应力混凝土梁的侵蚀中引入损伤因子,以考虑荷载的影响。总体而言,目前针对弯曲荷载下的氯盐侵蚀的研究主要以试验数据建立影响函数修正氯离子扩散系数,从而对荷载效应进行考虑,但相关的数值模拟研究成果较少,缺乏详细阐述。为此,本文以荷载、侵蚀时间为变量开展弯曲荷载与干湿循环共同作用下混凝土的氯盐侵蚀试验;介绍一种考虑荷载及干湿循环的数值模拟方法,并拟合荷载影响系数,对构件层次的氯离子扩散场和荷载场进行耦合分析。
1 模型的建立
1.1 非饱和状态下混凝土中氯离子的输运
氯离子在干湿交替区混凝土中的传输是典型的非饱和输运过程:氯离子除了随混凝土孔隙液离子质量分数梯度发生扩散外,还将随着孔隙液饱和度梯度发生对流作用。由于氯离子的输运发生于混凝土的孔隙溶液中,孔隙溶液饱和度必然会对氯离子的扩散速度造成影响。李春秋等[2, 11]提出了指数型、多项式型函数对氯离子扩散系数和孔隙饱和度之间的关系进行描述。本文参考文献[2,4],取非饱和状态下混凝土内水分及氯离子传输模型的一维形式为:
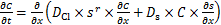 (1)
(1)
 (2)
(2)
式中:C为氯离子质量分数;s为孔隙液浓饱和度;Ds为水分扩散系数;DCl为氯离子扩散系数;r为饱和度影响系数,考虑到s与DCl呈线性关系,r=1;t为实际暴露时间。
对于氯离子扩散系数DCl,由于混凝土水化等作用的持续进行,混凝土的孔隙结构逐渐密实,会呈指数衰减,t时刻的扩散系数D(t)可按下式计算:
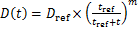 (3)
(3)
式中:Dref为时间tref对应的参照氯离子扩散系数;m为龄期衰减系数,与胶凝材料的环境及种类有关[4,12]。
对于水分扩散系数Ds,金伟良[4,13-14]等提出了不同的模型。本文采用刘鹏等[15]提出的简化的水分扩散模型,其形式如下。
湿润过程:
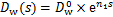 (4)
(4)
干燥过程:
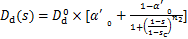 (5)
(5)
式中:Dw0和Dd0分别为湿润和干燥过程饱和状态水分扩散系数;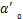 为相对湿度极低时Ds与Dd0的比值;sc为Ds/Dd0=1/2时的相对湿度;n1和n2分别为湿润和干燥过程中Dd变化速率的系数;e为自然底数。
为相对湿度极低时Ds与Dd0的比值;sc为Ds/Dd0=1/2时的相对湿度;n1和n2分别为湿润和干燥过程中Dd变化速率的系数;e为自然底数。
1.2 考虑荷载作用下的混凝土中氯离子的输运
荷载作用会对混凝土中的氯盐侵蚀速度产生影响,目前国内外学者通常基于试验数据对氯离子扩散系数进行修正,但采用的自变量也各有不同。WANG等[7-8]分别以弯曲荷载和裂缝宽度为变量建立函数对氯离子扩散系数进行修正;吴静新[16]以体积应变和孔隙率作为耦合变量,建立了荷载与氯盐侵蚀共同作用下的氯离子传输模型。AL-KUTTI[17]提出以标量损伤作为自变量考虑荷载的影响,可以体现应力对氯离子扩散速度的影响,且可推广到不同的混凝土材料。因此,本文采用AL-KUTTI提出的考虑结构损伤的氯离子扩散系数D,其表达式如下:
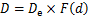 (6)
(6)
式中:De为不考虑结构损伤时的氯离子扩散系数,F(d)为以标量损伤d为自变量的混凝土损伤影响函数,刘鹏等[15]基于试验数据采用多项式形式对其进行了拟合。
AL-KUTTI[17]以混凝土弹性刚度的退化来描述混凝土损伤,得出标量损伤与混凝土应变之间的关系:
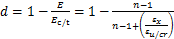 (7)
(7)
式中:εx为混凝土轴向应变,当εx<0即混凝土受压时,Ec/t取Ec,εu/cr取εu,当εx>0即混凝土受拉时,Ec/t取Et,εu/cr取εcr;Ec和Et分别为混凝土未受损伤时的受压割线模量和受拉割线模量;εu和εcr分别为混凝土的极限压应变和开裂应变;n为混凝土损伤时的材料参数,在受拉与受压时取值不同。
2 数值模型的建立
2.1 COMSOL物理场模块设置
本文使用COMSOL Multiphysics 5.2a实现多物理场的耦合分析,采用“固体力学”物理场实现混凝土受荷的模拟,采用“桁架”物理场实现钢筋受荷的模拟,采用“系数型偏微分方程”物理场实现干湿循环下氯离子输运的模拟。“系数型偏微分方程”模块的控制方程如下:
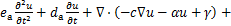
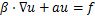 (8)
(8)
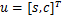 (9)
(9)
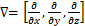 (10)
(10)
式中:c为扩散系数;a为吸收系数;f为源项;ea为质量系数;da为阻尼或质量系数;α为守恒通量对流系数;β为对流系数;γ为守恒通量源。本文中a,f,ea,β和γ均设置为0,da取1。
2.2 模型试算
为了检验模型的合理性,以干湿循环下3点受弯钢筋混凝土梁为对象进行模型试算分析。试算模型的条件参见文献[8]。其干湿循环制度以14 d为1个周期,干燥和湿润过程的时间相同。模型参数参照文献[2]。
取最后1个周期的湿润与干燥过程的计算结果进行分析。记湿润过程的起始时间为t1,结束时间为t2;干燥过程的起始时间为t3,结束时间为t4。以距中100 mm处为例,各个时间的饱和度和氯离子质量分数如图1所示。
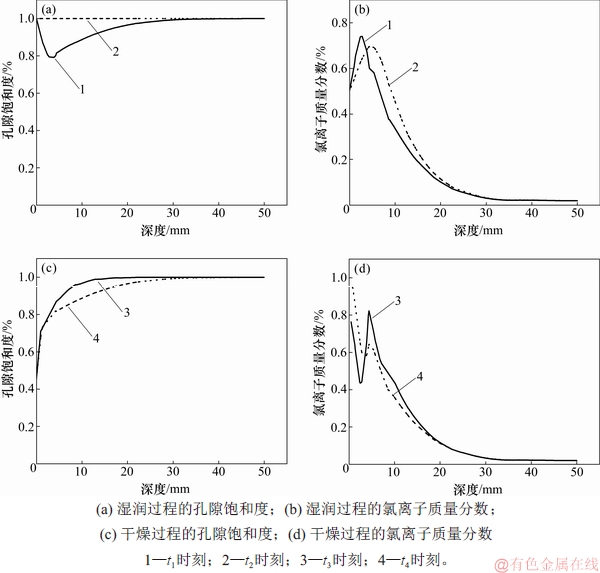
图1 模型试算结果
Fig. 1 Trial results of model
由图1(a)可见:在t1时刻前试件处于干燥过程,孔隙液随表面蒸发向外界迁移,滞后效应使孔隙饱和度曲线呈现显著的锋面。在t1时刻试件从干燥过程转变为湿润过程,孔隙渗流使得浅层处混凝土的饱和度有所提高,饱和度达到极小值。随着湿润过程不断进行,混凝土内孔隙饱和度逐渐恢复至t2时刻的1.0。由图1(b)可见:与此同时,外界氯离子随溶液渗入混凝土中,在混凝土的浅层区域发生对流和扩散的综合作用。由于对流效应对氯离子输运的贡献明显高于扩散效应,浅层中氯离子的补给速度高于其向内部扩散的速度,往往会形成浅层区形成1个峰值。
由图1(c)可见:在t3时刻,试件由湿润过程转入干燥过程,出现如前所述的饱和度下降锋面。随着干燥过程不断进行,内部孔隙液逐渐向外迁移,影响逐渐深入;锋面往混凝土内部推进,陡峭程度下降。由图1(d)可见:与此同时,氯离子随孔隙溶液向混凝土表层迁移,使得湿润过程中形成的峰值变得陡峭,接近表面处的氯离子质量分数也有所提高,如t3时刻曲线所示。随着干燥过程持续,氯离子随孔隙液逐渐向表面输运,峰值逐渐变小,表层处氯离子质量分数上升。
对于三点弯曲梁,从跨中到支座处,混凝土应变逐渐增大,损伤程度不断提高,氯离子扩散速率将会有所提高。不同深度处的氯离子试算结果如图2所示。由图2可见:对于同一深度的氯离子质量分数,由跨中到支座处呈现逐渐减小的趋势,可见该数值模型可以有效考虑荷载造成的混凝土损伤对氯盐侵蚀的影响,可进一步用于后续分析。
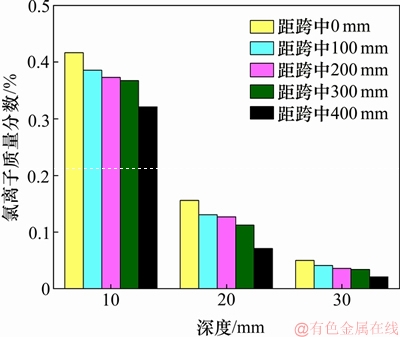
图2 不同深度处的氯离子质量分数试算结果
Fig. 2 Trial results of chloride ion mass fraction profile at different depths
3 试验验证
3.1 试验材料
本试验采用强度等级为C40的普通硅酸盐水泥、粒径为5~25 mm的碎石以及天然江砂。混凝土不掺加任何外加剂,采用普通自来水作为拌合水和养护水。试验采用的水灰比为0.4,混凝土中各材料用量为:水泥455 kg/m3,水182 kg/m3,砂755 kg/m3,石子1 465 kg/m3。其混凝土标准立方体试块28 d抗压强度平均值为49.8 MPa。
对本试验中采用的钢筋进行拉伸试验,测得直径8 mm钢筋的屈服强度和极限强度分别为308.2 MPa和484.9 MPa,直径14 mm钢筋的屈服强度和极限强度分别为471.7 MPa和628.1 MPa。
3.2 试件设计与制作
设计制作了7根钢筋混凝土梁试件,试件长×宽×高为1 000 mm × 150 mm × 180 mm,保护层厚度取35 mm,各试件具体参数见表1,试件配筋及加载方式如图3所示。表1中:S0仅用于确定混凝土梁的极限承载力,不进行氯盐侵蚀;S1,S2和S3进行182 d干湿循环;S4,S5和S6进行364 d干湿循环。文献[18]将钢筋混凝土构件正截面的受力裂缝控制等级分为3级,本文试验通过设置荷载比P/Pcr(即施加的弯曲荷载与极限弯曲承载力的比值)为0,23.7%和37.6%的试件分别对应一级、二级和三级裂缝控制等级。
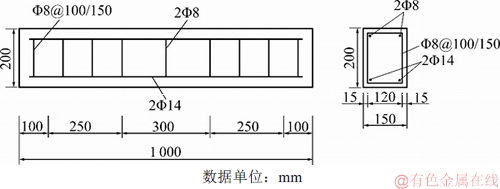
图3 钢筋混凝土梁尺寸和配筋图
Fig. 3 Dimension and reinforcements of specimens
表1 试件具体参数
Table 1 The specific parameters of test specimens
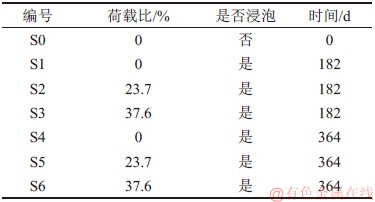
对进行干湿循环的试件(S1~S6)只保留其受拉下底面(150 mm × 1 000 mm)作为氯离子渗透面,将其他5个截面的表面浮浆磨去,用酒精清洗干净后,用环氧树脂涂刷封闭,保证氯离子只从底面进行渗透。
3.3 试验方法
待标准固化期结束后,首先对试件S0进行两点静力加载试验,确定S0极限承载力为255 kN。采用如图4所示的加载装置将S1~S6两两自锚,施加对应的弯曲荷载,通过螺杆上的力传感器监测施加在螺栓上的预紧力。
荷载施加完成后,将试件放置于质量分数为5%的NaCl溶液中进行干湿循环试验。每个干湿循环周期为14 d,干湿周期比例取1:1,以模拟海工环境下混凝土的干湿交替区域。由于试验周期较短,本文暂不考虑锚杆的应力松弛以及混凝土裂缝的自愈合行为。
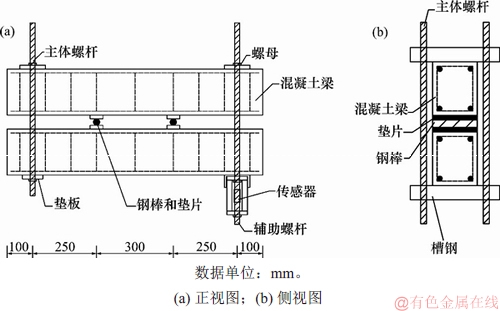
图4 弯曲荷载加载装置图
Fig. 4 Flexural loading devices

图5 试件取样位置
Fig. 5 Sampling position of specimen
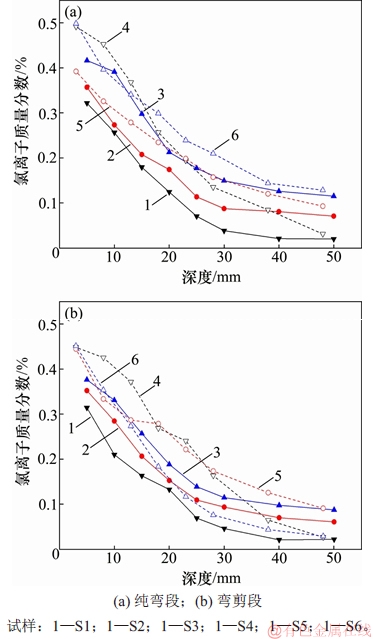
图6 试件氯离子质量分数与深度的关系
Fig. 6 Relationship between chloride ion mass fraction of specimens and depth
待干湿循环试验结束后,将试验梁取出,置于干燥处晾干7 d,随后用冲击钻在各开裂试件纯弯段、弯剪段沿侵蚀面竖直方向钻孔取粉,试件芯样取样位置如图5所示。最大深度取至50 mm处,同一位置沿深度方向,前20 mm每隔5 mm取1次粉样,30~50 mm每隔10 mm取1次粉样;参考文献[19],将粉末试样分别过0.63 mm筛,并装入铝盒中,置于(105±5) ℃的烘干箱中烘干2 h,取出放入干燥器冷却至室温,测定混凝土中水溶性氯离子(自由氯离子)质量分数。
3.4 试验结果分析
对纯弯段、弯剪段测点在各深度的氯离子质量分数分别计算平均值,得到不同荷载、侵蚀时间的6条试验梁不同受力部位的氯离子质量分数随深度变化曲线,如图6所示。
除S6弯剪段外,随弯曲荷载从无荷载增加至37.6%,对于相同侵蚀时间的试验梁(图6中实心图标和空心图标分别为182 d和364 d侵蚀时间下的结果),相同深度处的氯离子质量分数整体上增大。其主要原因是随着荷载的提高,试验梁受拉区混凝土的损伤程度提高,逐渐产生微观裂缝,导致其孔隙连通度增大;而随着宏观裂缝的出现和扩展,氯离子逐渐开始从裂缝内表面进行渗透。
除S6弯剪段外,随着侵蚀时间从182 d增加至364 d,对于相同弯曲荷载下的试验梁(即图6中同种形状图标),相同深度处的氯离子质量分数整体上增大。其原因是随着侵蚀时间延长,氯离子从侵蚀面不断向内输运,质量分数不断提高。
在S6试件弯剪段,测点5所在位置混凝土截面完好,与荷载裂缝之间存在较远的距离,氯离子扩散速度较慢。因此,S6弯剪段测得的氯离子质量分数较低是合理的。
通过图6对比可得:整体而言,相同深度处纯弯段的氯离子质量分数高于弯剪段。这是因为对于试验梁,纯弯段受到的弯矩较大,受拉区拉应力较高,损伤程度较大,氯离子的输运速度明显加快。
4 数值分析
4.1 模型参数的确定
在“全局定义”版块输入模型计算所需参数及函数,对试验梁模拟时采用的参数如表2所示。
表2 模型参数
Table 2 Parameters of model

在混凝土表层对流区深度内部,氯离子的渗透主要以扩散为主,可以采用Fick第二扩散定律反映不同位置、时间的氯离子质量分数[8,20]:
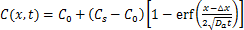 (11)
(11)
式中:C(x, t)为暴露时间t深度为x处的氯离子质量分数;C0为混凝土中的初始氯离子质量分数;Cs为混凝土表面氯离子质量分数;x为据混凝土表面的深度;Da为表观扩散系数;△x为表面对流区深度;erf(x)为高斯误差函数。
由于S1和S4试验数据没有出现明显的对流区,本文认为其对流区深度小于5 mm,在拟合时采用5 mm以后的试验数据。此外,假定混凝土中的初始氯离子质量分数为0,故C0 =0。借助MATLAB数据拟合工具箱,应用式(11)对无荷载的S1和S4各测点数据进行拟合分析,结果如图7所示,得到182 d和364 d氯离子表观扩散系数分别为1.014 0 mm2/d和0.904 4 mm2/d。结合式(3),设tref为28 d,计算得28 d参考氯离子扩散系数Dref, 28 = 1.73×10-11m2/s,龄期衰减系数m = 0.19。
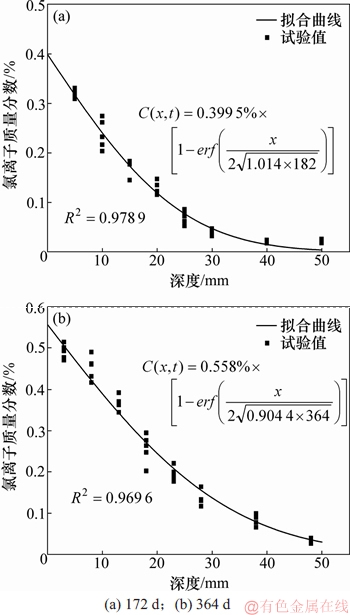
图7 表观氯离子扩散系数拟合
Fig. 7 Apparent chloride diffusion coefficient fitting
根据HALL[21]和LEECH[22]建议,湿润过程水分扩散系数的参数n1取6。干燥过程水分扩散系数相关参数参考文献[21-24]取值。
AL-KUTTI根据试验数据拟合的荷载修正函数在应变较大时与其他文献结果有较大偏差[15],因此,在文献[25]的试验数据上,拟合了以标量损伤为变量的荷载影响函数:
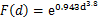 (12)
(12)
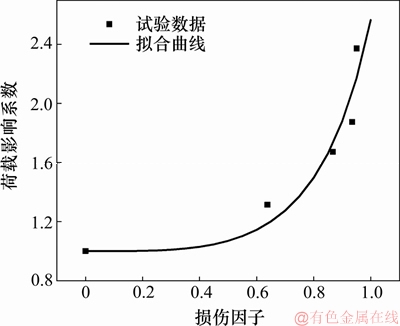
图8 荷载影响系数与混凝土标量损伤关系图
Fig. 8 Relationship between concrete scalar damage and loading influence coefficient
其形式如图8所示。由于现有研究中反映混凝土应变与氯离子扩散规律的试验数据不足,其适用性有待更多试验进行验证。此外,由于压应变对氯离子扩散系数的影响尚未有定论[5-6,15],且本文的研究对象为受拉区,故模拟中仅考虑受拉损伤。
4.2 模型的建立
材料的参数取值按照材性试验结果输入;采用内置的Ottosen模型作为混凝土的破坏准则。
建立“固体力学”物理场(混凝土),设置支座条件为一端铰接、一端滑动,在加载面添加均匀分布荷载;建立“桁架”物理场(钢筋),通过“指定位移”使钢筋和混凝土变形协调;建立“系数型偏微分方程”(氯离子),根据式(1) ~ (2)对该控制方程的参数设置守恒通量对流系数α和扩散系数c。α对于水分传输方程取为0,对于氯离子传输方程α = Ds×ds/dz;根据式(3)和(6)考虑荷载和龄期对氯离子扩散系数c的影响,其参数确定过程见4.1节。
因试验采用单面侵蚀,为模拟氯离子的一维渗透,在氯离子侵蚀面设置“狄氏边界条件”,指定边界质量分数为0.5%;其他5个面边界条件设置为“零通量”。
由于试验所关注的对象为试验梁受拉区50 mm深度内的氯离子质量分数,通过“加密层”对受拉区边缘的网格进行精密划分。
干湿循环和荷载耦合分析通过COMSOL研究步实现:步骤1为稳态计算,选择固体力学物理场接口,计算混凝土梁在荷载作用下的力学响应;步骤2和3为瞬态计算,分别计算湿润和干燥过程荷载作用下混凝土梁中氯离子的输运进程;后续步骤皆为干湿循环过程。每1个步骤调用上1个步骤的解进行运算。
4.3 计算结果
以S2,S4和S6为例,提取试件纯弯段、弯剪段的测点有限元结果与试验数据进行对比,结果如图9所示。由图9可见:数值模拟与试验研究的结果整体上吻合良好;对于施加弯曲荷载的试验梁,由于宏观裂缝的出现,各测点氯离子质量分数的数据离散性较大,但COMSOL拟合结果更为贴近上限值,较为保守;对于S6弯剪段,如图9(f)所示,测点5的数据明显偏离数值模拟结果,这与3.4中的试验结果分析相吻合。因此,本文通过混凝土力学损伤来考虑荷载对氯离子在混凝土内输运影响的方法合理可行,所采用的力学损伤函数较好地模拟本文的试验结果。
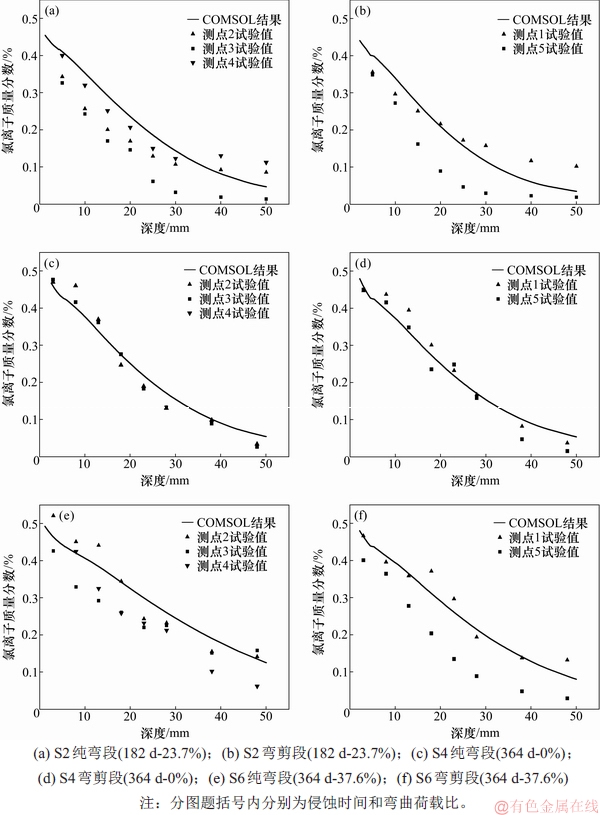
图9 氯离子质量分数数值模拟结果与试验结果对比
Fig. 9 Comparison of numerical simulation and experiments on chloride ion mass fraction
图10所示为COMSOL计算所得的混凝土梁轴向应变云图(以182 d试验梁为例)。试验梁的轴向应变与所受的弯曲荷载相对应。S2跨中区域最大拉应变达到3.09×10-4与混凝土的受拉开裂应变较为接近。S3跨中区域最大拉应变达到7.94×10-4,远大于混凝土的受拉开裂应变。可以推断,此时混凝土达到开裂状态,出现多条宏观裂缝。试件的应变情况与试验方案设定的3个裂缝控制等级要求基本符合。
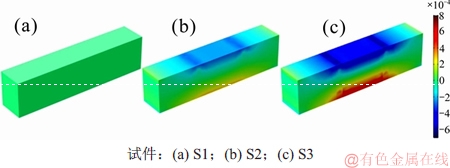
图10 轴向应变图
Fig. 10 Diagrams of strain along axial direction
图11所示为182 d的3条试验梁的混凝土损伤情况。由图11可知:随着荷载的提高,混凝土的标量损伤沿着深度方向和跨中方向增长,损伤区域与损伤程度扩大,与试验梁的荷载、应变状态相一致。
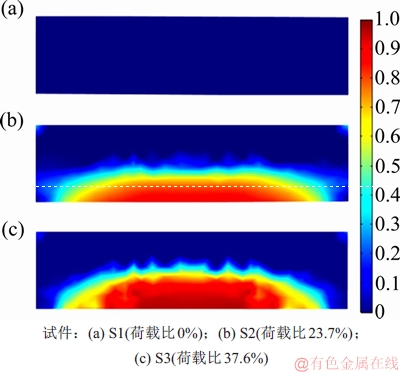
图11 182 d试件标量损伤d云图
Fig. 11 Scalar damage parameter d diagram of 182 d specimens
图12所示为沿侵蚀面不同深度处的氯离子质量分数分布(以梁S3为例)。由图12可知:对于同一试验梁同一深度处,氯离子质量分数在纯弯段基本保持在一个水平,在弯剪段往远离跨中方向逐渐降低,这是由于在纯弯段弯矩保持定值,梁受拉区的轴向应力在纯弯段基本保持一致,损伤程度接近,氯离子侵蚀速度接近;而弯矩在弯剪段往两端逐渐递减,轴向应力逐渐降低,损伤程度也随之降低,氯离子侵蚀速度逐渐降低。
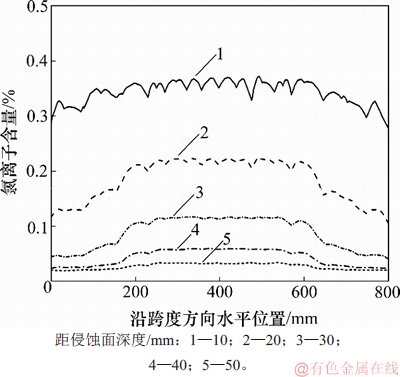
图12 沿侵蚀面不同深度处的氯离子质量分数
Fig. 12 Chloride ion mass fractions at different depths from erosion surface
5 结论
1) 随着弯曲荷载和侵蚀时间的提高,混凝土梁内的氯离子质量分数不断提高。对于四点加载的混凝土梁的受拉区,纯弯段的氯离子质量分数明显高于弯剪段氯离子质量分数。
2) 考虑混凝土力学损伤可以针对不同损伤部位设置不同的氯离子扩散系数,从而考虑荷载作用对氯离子在混凝土内传输特性的影响。
3) 采用COMSOL模拟干湿循环下承受弯曲荷载的混凝土梁的氯盐侵蚀,所提出的荷载影响函数可以较好地拟合本文的试验结果。
参考文献:
[1] ABABNEH A, BENBOUDJEMA F, XI Y. Chloride penetration in nonsaturated concrete[J]. Journal of Materials in Civil Engineering, 2003, 15(2) : 183-191.
[2] 李春秋, 李克非. 干湿交替下表层混凝土中氯离子传输: 原理、试验和模拟[J]. 硅酸盐学报, 2010, 38(4): 581-589.
LI Chunqiu, LI Kefei. Chloride ion transport in concrete under drying-wetting cyckes: theory, experiment and modeling[J]. Journal of Chinese Ceramic Society, 2010, 38(4): 581-589.
[3] XI Y, BA ANT Z P. Modeling chloride penetration in saturated concrete[J]. Journal of Materials in Civil Engineering, 1999, 11(1): 58-65.
ANT Z P. Modeling chloride penetration in saturated concrete[J]. Journal of Materials in Civil Engineering, 1999, 11(1): 58-65.
[4] 金伟良. 氯盐环境下混凝土结构耐久性理论与设计方法[M]. 北京: 科学出版社, 2011: 127-147.
JIN Weiliang. Durability theory and design method of concrete structures in chloride environment[M]. Beijing: Science Press, 2011: 127-147.
[5] YE Hailong, FU Chuanqing, JIN Nanguo, et al. Influence of flexural loading on chloride ingress in concrete subjected to cyclic drying-wetting condition[J]. Computers & Concrete, 2015, 15(2): 183-198.
[6] WANG Yuanzhan, LIN Chen’anpan, CUI Yanqiang. Experiments of chloride ingression in loaded concrete members under the marine environment[J]. Journal of Materials in Civil Engineering, 2014, 26(6): 04014012.
[7] WANG Hailong, DAI Jianguo, SUN Xiaoyan. Chloride transport in concrete under sustained flexural loading[J]. Magazine of Concrete Research, 2017, 69(5): 245-254.
[8] 陆春华, 刘荣桂, 崔钊玮, 等. 干湿交替作用下受弯开裂钢筋混凝土梁内氯离子侵蚀特性[J]. 土木工程学报, 2014, 47(12): 82-90.
LU Chunhua, LIU Ronggui, CHUI Zhaowei , et al. Study on chloride penetration into flexural cracked reinforced concrete beams subjected to drying-Wetting cycles[J]. China Civil Engineering Journal, 2014, 47(12): 82-90.
[9] 蔡健, 蚁原野, 陈庆军, 等. 荷载场和氯离子扩散场共同作用下的钢筋混凝土构件分析[J]. 水运工程, 2017(4): 33-41.
CAI Jian, YI Yuanye, CHEN Qingjun, et al. Analysis on reinforced concrete member under combined action of load and chloride diffusion[J].Port and Waterway Engineering, 2017(4): 33-41.
[10] 蔡健, 魏沐杨, 罗赤宇, 等. 弯曲荷载与氯盐侵蚀共同作用下的预应力混凝土梁耐久性能研究[J]. 工程力学, 2018, 35(7): 208-218, 242.
CAI Jian, WEI Muyang, LUO Chiyu, et al. Durability of prestressed concrete beams under simultaneous flexural load and chloride erosion[J]. Engineering Mechanis, 2018, 35(7): 208-218, 242.
[11] CLIMENT M A, VERA G D, JES S F L, et al. A test method for measuring chloride diffusion coefficients through nonsaturated concrete: Part I. The instantaneous plane source diffusion case[J]. Cement & Concrete Research, 2007, 37(5): 714-724.
S F L, et al. A test method for measuring chloride diffusion coefficients through nonsaturated concrete: Part I. The instantaneous plane source diffusion case[J]. Cement & Concrete Research, 2007, 37(5): 714-724.
[12] 中国工程院土木水利与建筑学部工程结构安全性与耐久性研究咨询项目组. 混凝土结构耐久性设计与施工指南[M]. 中国建筑工业出版社, 2004: 16-18.
Consultative Project Group on Safety and Durability of Engineering Structures, Ministry of Civil Water Conservancy and Architecture, Chinese Academy of Engineering. Guide to Durability Design and Construction of Concrete Structures[M]. China Architecture and Building Press, 2004: 16-18.
[13] 延永东. 氯离子在损伤及开裂混凝土内的输运机理及作用效应[D]. 杭州: 浙江大学建筑工程学院, 2011: 40-55.
YAN Yongdong. Transportation of chloride ion in damaged and cracked concrete and its action[D]. Hangzhou: Zhejiang University. College of Civil Engineering and Architecture, 2011: 40-55.
[14] 张奕. 氯离子在混凝土中的输运机理研究[D]. 杭州: 浙江大学建筑工程学院, 2008: 32-40.
ZHANG Yi. Mechanics of chloride ions transportion in concrete[D]. Hangzhou: Zhejiang University. College of Civil Engineering and Architecture, 2008: 32-40.
[15] 刘鹏, 宋力, 余志武. 模拟干湿环境对混凝土内水分影响深度的影响[J]. 华南理工大学学报(自然科学版), 2014, 42(2): 64-73.
LIU Peng, SONG Li, YU Zhiwu. Effect of simulated drying-wetting environment on water influence depth in concrete[J]. Journal of South China University of Technology (Natural Science Edition), 2014, 42(2): 64-73.
[16] 吴静新. 混凝土内氯离子传输模型及其数值研究[D]. 哈尔滨: 哈尔滨工业大学土木工程学院, 2012: 25-26.
WU Jingxin. Modeling and simulation of chloride ions transmission in concrete[D]. Harbin: Harbin Institute of Technology. School of Civil Engineering, 2012: 25-26
[17] AL-KUTTI W. Enhancement in chloride diffusivity due to flexural damage in reinforced concrete beams[J]. Journal of Materials in Civil Engineering, 2014, 26(4): 658-667.
[18] 中华人民共和国住房和城乡建设部. 混凝土结构设计规范[M]. 中国建筑工业出版社, 2015: 88-97.
Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Code for Design of Concrete Structures [M]. China Architecture and Building Press, 2015: 88-97.
[19] 中华人民共和国交通部. 水运工程混凝土试验规程[M]. 人民交通出版社, 1998: 202-207.
Ministry of Transport of the People's Republic of China. Testing code of concrete for port and waterwog engineering[M]. China Communications Press, 1998: 202-207.
[20] 金伟良, 金立兵, 延永东, 等. 海水干湿交替区氯离子对混凝土侵入作用的现场检测和分析[J]. 水利学报, 2009, 40(3): 111-118.
JIN Weiliang, JIN Libing, YAN Yongdong, et al. Field inspection on ion-intrusion effect of seawater in dry-wet cycling zone of concrete structures[J]. Journal of Hydraulic Engineering, 2009, 40(3): 111-118.
[21] HALL C. Water sorptivity of mortars and concretes: A review[J]. Concrete Research,1989,41(147): 51-61.
[22] LEECH C, LOCKINGTON D, DUX P. Unsaturated diffusivity functions for concrete derived from NMR images[J]. Materials & Structures, 2003, 36(6): 413-418.
[23] 关鹏. 干湿循环下混凝土氯离子传输模型研究[J]. 混凝土. 2012(11): 7-11.
GUAN Peng. Study on chloride trandport model in concrete under drying-wetting cycles[J]. Concrete, 2012(11): 7-11.
[24] 林刚, 刘应华. 干湿交替下混凝土氯离子运输模拟[J]. 武汉轻工大学学报, 2009, 28(3): 68-71.
LIN Gang, LIU Yinghua. Modeling chloride penetration into concrete under drying-wetting cycles[J]. Journal of Wuhan Polytechnic University, 2009, 28(3): 68-71.
[25] 付传清, 屠一军, 金贤玉, 等. 荷载和环境共同作用下混凝土中氯离子传输的试验研究[J]. 水利学报, 2016, 47(5): 674-684.
FU Chuanqing, TU Yijun, JIN Xianyu, et al. Experimental study on chloride transport in concrete under environmental and loading coupling conditions[J]. Journal of Hydraulic Engineering, 2016, 47(5): 674-684.
(编辑 秦明阳)
收稿日期: 2019 -03 -01; 修回日期: 2019 -05 -10
基金项目(Foundation item):国家自然科学基金资助项目(51578246);广东省自然科学基金资助项目(2017A030313263);华南理工大学亚热带建筑科学国家重点实验室自主研究课题(2018ZC11)(Project(51578246) supported by the National Natural Science Foundation of China; Project(2017A030313263) supported by the Natural Science Foundation of Guangdong Province; Project(2018ZC11) supported by the Independent Research Program of State Key Laboratory of Subtropical Building Science of South China University of Technology)
通信作者:陈庆军,博士,副教授,从事结构理论、结构仿真分析等研究;E-mail:qjchen@scut.edu.cn