扬声器对低频短纯音信号响应的研究
张平柯
(湖南第一师范学院 数学物理系,湖南 长沙,410002)
摘 要:通过建立并求解扬声器纸盆在低频短纯音信号驱动下的运动微分方程,并借助MAPLE软件分析扬声器纸盆运动情况,给出扬声器纸盆的速度与时间关系的解析式及其速度-时间图像的描述方法,分析影响扬声器瞬态特性的因素,并对理论研究结果进行实验检验。此外,还提供一种测量扬声器品质因素Q的可能方法。研究结果表明:扬声器前、后沿特性具有相关性;扬声器的机械品质因素Qm与电品质因素Qe对其前、后沿特性影响有等效性;真正影响扬声器瞬态特性的是扬声器的总品质因素Qt,对一定频率范围内的短纯音信号,若扬声器的Qt越小,则其前、后沿特性就越好,但Qt过小会导致声压频率特性劣化;在设计扬声器时,应综合考虑瞬态响应与声压频率特性的要求确定合适的Qt。
关键词:扬声器;品质因素;短纯音信号
中图分类号:TN722 文献标志码:A 文章编号:1672-7207(2010)06-2274-08
Loudspeakers’ response to low-frequency tone burst signals
ZHANG Ping-ke
(Department of Mathematics and Physics, Hunan First Normal College, Changsha 410002, China)
Abstract: Through establishing and solving differential equation of motion of the loudspeaker’s cone driven by low-frequency tone burst signals, the cone’s motion was analyzed with MAPLE software, analytic expression of the cone’s velocity- time relation and a way of describing its velocity-time curve were given. Factors affecting the speaker’s transient characteristics were studied, and theoretical results were tested by experiment. In addition, a possible way was proposed to measure the speaker’s quality factor Q. The results show that the characteristics of the front and back edges of the speakers are interrelated; both the speaker’s mechanical quality factor (Qm) and its electrical quality factor (Qe) have equivalent influence on the characteristics of the front and back edges of the speaker. Total quality factor (Qt) really affects the speaker’s transient characteristics. As to tone burst signals in a certain range of frequency, the smaller the Qt of the speaker, the better its characteristics of the front and back edges. But too small Qt leads to degradation of sound pressure frequency characteristics. When designing speakers, the transient response and sound pressure frequency characteristics should be comprehensively taken into consideration to determine the appropriate Qt.
Key words: loudspeaker; quality factor; tone burst signals
人们通常采用机电类比法对扬声器进行定量研 究[1-4],将扬声器振动系统等效为交流电路,将振动系统元件特性参数等效为电路元件特性参数,将振动系统的状态参量等效为电路的状态参量。这种方法的优点在于人们可以利用交变电路系统化的研究成果,研究扬声器的振动情况,得出声压频率特性、平均声功率等反映扬声器及其系统稳态特性的技术指标。由于一般音乐信号中存在大量的猝发性信号,因此,扬声器系统的稳态技术指标并不能全面反映其对音乐信号的响应,短纯音信号较接近真实音乐信号,扬声器对短纯音信号的响应能更客观地反映其性能[5]。在短纯音电信号的驱动下,由于扬声器的固有特性不可避免地会在振动的启动阶段(前沿)和结束阶段(后沿)产生瞬态失真。分析扬声器对短纯音信号的响应有助于提高扬声器系统的电声还原质量。机电类比法不太适用于对扬声器纸盆运动的瞬态分析,为此,本文作者通过求解在短纯音信号驱动下扬声器纸盆运动的微分方程,并利用MAPLE 软件[6]代入已知参数绘制响应曲线,同时进行实际测量,将测量结果与理论研究结果进行对照,以寻找影响扬声器瞬态特性的因素。
1 在短纯音信号驱动下纸盆运动微分方程及其求解
在正弦驱动力下工作的扬声器是一个受迫振动系统,它所受到的驱动力是罐形磁场对音圈施加的安培力,设扬声器受到的驱动电压为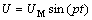 (其中:UM为驱动电压幅值;p为驱动电压的圆频率;t为时间),当音圈在罐形磁场的均匀区域振动时,该力可表示为
(其中:UM为驱动电压幅值;p为驱动电压的圆频率;t为时间),当音圈在罐形磁场的均匀区域振动时,该力可表示为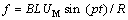 (其中:B为罐形磁场的磁感应强度;L为音圈绕线的总长度;R为音圈的直流电阻)。
(其中:B为罐形磁场的磁感应强度;L为音圈绕线的总长度;R为音圈的直流电阻)。
纸盆运动时受到的阻力由2部分组成:一部分是机械阻力,它主要由空气阻力形成,在速度不太大的情况下,阻力与速度成正比,即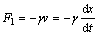 (其中,
(其中,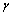 为机械阻力系数);另一部分是音圈受到的电磁
为机械阻力系数);另一部分是音圈受到的电磁
阻力,它可以表示为: (其中,
(其中,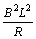 为电阻力系数)。因此,纸盆受到的总阻力为
为电阻力系数)。因此,纸盆受到的总阻力为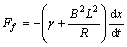 。
。
设扬声器的等效振动质量为m,扬声器振动系统的劲度系数为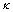 ,纸盆离开平衡位置的位移为x,根据牛顿第二定律,有:
,纸盆离开平衡位置的位移为x,根据牛顿第二定律,有:
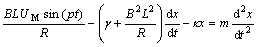
若令驱动力幅 ,总阻力系数
,总阻力系数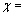
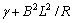 ,则扬声器的振动微分方程为:
,则扬声器的振动微分方程为:

设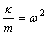 ,
,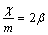 ,
, ,则上式化为:
,则上式化为:
 (1)
(1)
式(1)的解[7-8]分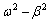 >0,
>0,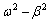 <0,
<0,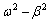 =0这3种情况进行讨论。
=0这3种情况进行讨论。
当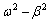 >0时,式(1)满足初始条件
>0时,式(1)满足初始条件 ,
,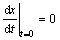 的解为:
的解为:
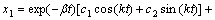
 (2)
(2)
式中:
 ;
;
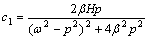 ;
;
 。
。
当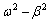 <0时,式(1)满足初始条件
<0时,式(1)满足初始条件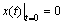 ,
,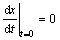 的解为:
的解为:
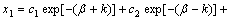
 (3)
(3)
式中:
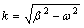 ;
;
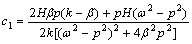 ;
;
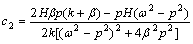 。
。
式(2)和(3)右边前面部分对扬声器起始阶段的瞬态特性影响很大,但经历充分长时间后,都将变成0。最后一项形式相同,引入:
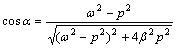 ;
;

则
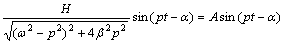 (4)
(4)
即经历充分长时间后,扬声器将作与驱动力频率相同的运动,但它们间存在相位差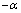 。也就是说,在
。也就是说,在
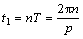 (n为整数)时撤除驱动力,扬声器的振
(n为整数)时撤除驱动力,扬声器的振
动位移、速度并不会回到初始状态。这时,它具有由速度和位移决定的动能和势能,还将产生余振。其振动方程为典型的阻尼振动方程:
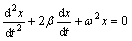
当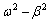 >0时,其解为:
>0时,其解为:
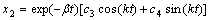
x2决定了扬声器停振过程中的瞬态特性。其中:c3和c4由x和v在t1时刻的值xt1和vt1来决定,可解得:c3=xt1;c4=(vt1+βxt1)/k。
若将x2的时间起点放到与驱动力相同的时间起点上,则有:
其中:t>t1。
因此,当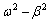 =0时,在短纯音信号驱动下,扬声器纸盆位移可用下面的分段函数表示:
=0时,在短纯音信号驱动下,扬声器纸盆位移可用下面的分段函数表示:

当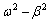 <0时,方程的解为:
<0时,方程的解为:
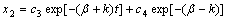
可解得:
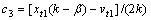 ;
;
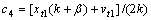
因此,当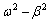 <0时,在短纯音信号驱动下,扬声器纸盆位移可用如下分段函数表示:
<0时,在短纯音信号驱动下,扬声器纸盆位移可用如下分段函数表示:
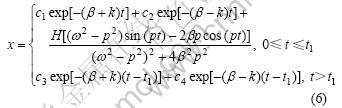
这2种情况下的c1,c2,c3和c4是不同的。
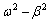 =0的情况可从前2种情况逼近求解。
=0的情况可从前2种情况逼近求解。
2 扬声器对短纯音信号响应的分析
对扬声器来说,人们关心的是它在聆听位置上的声压特性。而声压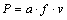 (其中,f为频率,v为扬声器纸盆振动速度,a为比例系数),因此,人们更关心的是扬声器纸盆的速度。将式(5)和(6)对时间求导,可得纸盆的瞬时速度。
(其中,f为频率,v为扬声器纸盆振动速度,a为比例系数),因此,人们更关心的是扬声器纸盆的速度。将式(5)和(6)对时间求导,可得纸盆的瞬时速度。
(1) 当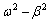 >0时,
>0时,
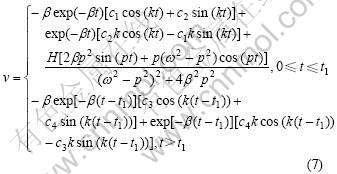
(2) 当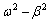 <0时,
<0时,
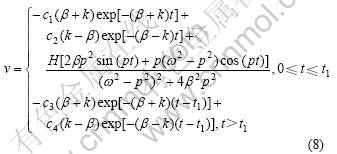
下面分析1只口径为200 mm的低音扬声器对低频短纯音信号的响应情况。
实测该扬声器音圈直流电阻R=7 Ω,谐振频率f0=38 Hz,总品质因素Qt=0.73[9-10]。根据振动理论,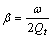 =163.5,它比
=163.5,它比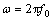 小,应该用式(7)进行分析;H与驱动电压有关,是一个可以改变的量,因此,可任选。利用MAPLE10作出f=f0=38 Hz时纸盆在0~0.45 s内振动的v-t曲线,如图1所示。
小,应该用式(7)进行分析;H与驱动电压有关,是一个可以改变的量,因此,可任选。利用MAPLE10作出f=f0=38 Hz时纸盆在0~0.45 s内振动的v-t曲线,如图1所示。
从图1可见:第1个速度峰的高度与稳定后的速度峰高度之比约为0.60,而非理想值1.00;余振峰与稳定速度峰的比值约为0.47,而非理想值0。

图1 f=f0时扬声器纸盆振动的理论v-t曲线
Fig.1 Theoretical v-t curve of cone vibration when f=f0
3 扬声器对短纯音信号响应的实测
在进一步分析扬声器的前、后沿特性与Qt的关系之前,先通过实验测出纸盆的速度-时间图像,以确定计算结果与实际情况的符合程度。
通常用麦克风检测扬声器的近场声压,并借助音频分析软件进行分析。但采用这种方法精度很难达到要求。实验用的扬声器是一种双音圈扬声器,其设计目的在于可灵活变换阻抗适合不同场合应用。将短纯音电信号加到1个音圈上,驱动纸盆振动,在另一个音圈上就会因为电磁感应而产生与纸盆的振动速度成正比的感应电动势E=BLv(其中:B为磁感应强度;L为线圈绕线总长度)。因此,通过计算机分析E的时间变化规律就可以发现速度的时间变化规律,描绘出纸盆振动的v-t图像。
图2所示是用该方法测得的实验扬声器在f=f0=38 Hz的短纯音信号驱动下的v-t曲线。
根据图2求得第1个速度峰的高度与稳定后速度峰高度之比约为0.59,第1个余振速度峰与稳定速度峰的比值约为0.47,测量结果与理论结果相吻合。
改变短纯音信号的频率,将测量结果与计算机模拟所得结果相比较,发现两者都很一致。
4 Qt对瞬态特性和声压频率特性的影响
设扬声器的谐振频率f0=38 Hz。通过计算机模拟研究不同频率的短纯音信号驱动下的纸盆v-t曲线。
图3~5所示分别是驱动信号频率f为38,25和75 Hz时的一组纸盆v-t曲线。从图3~5可以看出:只要驱动信号的频率在一定范围内,Qt越小,扬声器对短纯音信号的前、后沿响应越好。但Qt过小会使声压频率特性劣化。图6所示是根据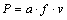 用计算机模拟的f0=38 Hz的扬声器在不同Qt时的声压频率特性。
用计算机模拟的f0=38 Hz的扬声器在不同Qt时的声压频率特性。

图2 f=f0时扬声器纸盆振动的实测v-t曲线
Fig.2 Measured v-t curve of cone vibration when f=f0
图3 Qt对38 Hz的短纯音信号的瞬态响应的影响
Fig.3 Influence of Qt on transient response of 38 Hz tone burst signal
图4 Qt对25 Hz的短纯音信号的瞬态响应的影响
Fig.4 Influence of Qt on transient response of 25 Hz tone burst signal
从图6可以看出:Qt=0.707的扬声器的声压频率特性最平坦,这与文献[11]中的结论是一致的。
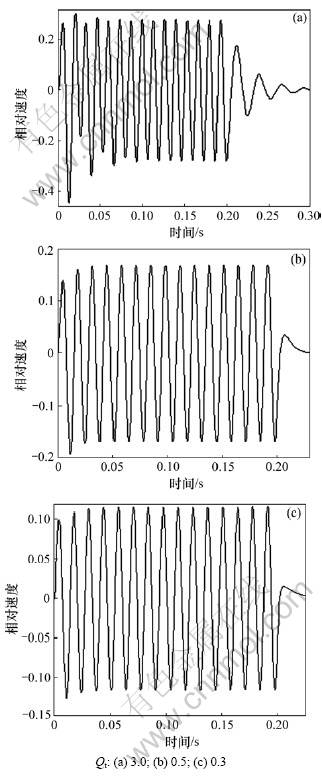
图5 Qt对75 Hz的短纯音信号的瞬态响应的影响
Fig.5 Influence of Qt on transient response of 75 Hz tone burst signal
但从图1和图2可以看出:此时扬声器的瞬态特性并不是很理想,反之,当Qt很小时,虽然扬声器对单一频率的短纯音信号瞬态响应较好,但声压频率特性很差,低音放不出来。因此,扬声器的瞬态特性与声压频率特性之间存在不可调和的矛盾。经折中考虑,Qt取0.5~0.7可以获得良好的综合性能。
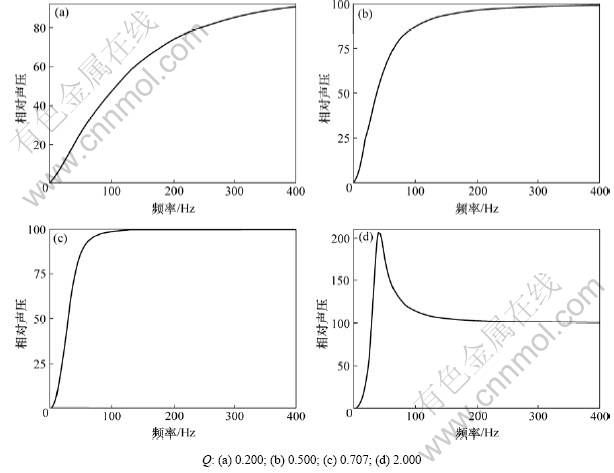
图6 Qt对声压频率特性的影响
Fig.6 Influence of Qt on pressure-frequency characteristics
5 扬声器的Qm与Qe的等效性
叶希鹏等[12-13]认为:扬声器的机械品质因素Qm主要影响其前沿响应,为保证扬声器的良好的前沿响应,Qm应该比较大。扬声器的电品质因素Qe主要影响其后沿响应,为保证扬声器的良好的后沿响应,Qe应该比较小。
本文作者对这种“Qm与Qe对扬声器前、后沿特性具有不同影响”的观点存在疑问。从前面的讨论可知:总阻力系数为机械阻力系数与电阻力系数之和。从对总阻力系数 的贡献来看,
的贡献来看,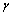 与B2L2/R是等价的,它们任何一个增大都将导致
与B2L2/R是等价的,它们任何一个增大都将导致 增大,从而导致Qt减小。而Qt的变化总是同时影响系统的前沿特性和后沿特性。为了证实这一点,在实验扬声器上串联2 kΩ的电阻,这时可认为系统的Qe已经变为原来的287倍(2007/7),根据Qm与Qe的并联关系[14-15],可不考虑Qe的影响,即可认为Qt=Qm(更严格地讲,应该将R=7 Ω和Rg=2 kΩ代入
增大,从而导致Qt减小。而Qt的变化总是同时影响系统的前沿特性和后沿特性。为了证实这一点,在实验扬声器上串联2 kΩ的电阻,这时可认为系统的Qe已经变为原来的287倍(2007/7),根据Qm与Qe的并联关系[14-15],可不考虑Qe的影响,即可认为Qt=Qm(更严格地讲,应该将R=7 Ω和Rg=2 kΩ代入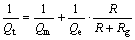 [11],得到Qt=Qm的结论)。利用前述的测试方法,可获得扬声器在f=f0时的纸盆振动v-t曲线,见图7。
[11],得到Qt=Qm的结论)。利用前述的测试方法,可获得扬声器在f=f0时的纸盆振动v-t曲线,见图7。
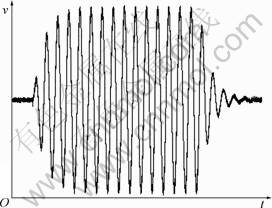
图7 消除电阻尼影响后扬声器纸盆的v-t曲线
Fig.7 v-t curve of cone after elimination of electrical damping implication
比较图7和图2可见:虽然Qm没有变化,只是Qe产生了变化(更严格地说是Qt产生了变化),但Qe变化影响的不仅是后沿特性,而且包括前沿特性。
用尝试法,通过计算机模拟,发现当系统的Qt取3时,所得到的图像与实验所测得的图像高度相似(见图3),这表明此时系统的Qm=3。图7与图3(a)所示的v-t曲线的相似性也表明前后沿特性的变化并不能反映到底是Qm还是Qe发生了变化。换句话说,Qm和Qe对扬声器的前、后沿特性产生的影响等效,真正影响扬声器前、后沿特性的是Qt,并且扬声器的前沿特性与后沿特性是相关的,前沿特性好的扬声器,后沿特性也好;前沿特性差的扬声器,后沿特性也差。
通过对扬声器的工作原理进行分析发现:Qm与Qe的形成机制是不一样的,Qm与Qe对扬声器的影响也不尽相同。如罐形磁场的磁感应强度B增加,会降低Qe,同时,还会使扬声器的灵敏度提高,因此,Qe较小的扬声器其灵敏度一般较高。在扬声器Qt一定时,如何搭配Qm与Qe需进行研究。但也许正是Qm与Qe对扬声器某些技术指标影响不相同,造成了“Qm和Qe的对扬声器的前、后沿特性影响也不一样”的 误解。
6 测量扬声器Q的一种可能方法
通过前面的分析,提出一种有效测量扬声器Q的新方法。
首先,用实验方法获取扬声器的纸盆振动的v-t曲线(在测Qm时应给扬声器串上1个充分大的电阻),将它储存到电脑中作为比较标准。然后,以Qt作为变量,以一定的步进值从小到大或从大到小(步进值越小,测量的精度越高)变化,让计算机通过式(7)(Qt>0.5时)或式(8)(Qt<0.5时)进行循环运算并作图,利用图像比较软件将每次作出的图与标准图像进行比较。当比较结果一致(可以设定允许的偏差值)时,终止程序运行,并输出此时的Qt。
测得Qt和Qm后,可以利用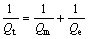 的关系式,由计算机直接算出Qe。
的关系式,由计算机直接算出Qe。
在开发专用的图像比较软件时,可利用扬声器前后沿特性的相关性,将比较重点放在前沿特性上,只需比较第1个速度峰的高度与稳定后速度峰高度之比。
可采用以上同样的方法对封闭式扬声器箱进行 讨论。
7 结论
(1) 分析了扬声器在低频短纯音信号驱动下的振动情况,给出了描述扬声器的速度与时间关系的解析式及速度-时间曲线的计算机作图法,并用实验证明了这种方法的正确性。
(2) 从理论上分析了机械品质因素Qm与电品质因素Qe对扬声器的前后沿特性影响的等效性,指出了扬声器前后沿特性的相关性。实验证明真正影响扬声器前后沿特性的是总品质因素Qt:扬声器的Qt越小,其前后沿特性就越好,但Qt太小,会导致声压频率特性的严重劣化。经综合考虑,Qt为0.5~0.7较合适(此结论仅对安放在自由空间和无限大障板上的扬声器有效,如果将扬声器装入音箱中,还必须考虑音箱的具体结构确定其Qt)。
(3) 提出了一种测量扬声器和封闭式扬声器箱品质因素Q的可能方法。
(4) 由于在高频时扬声器纸盆将产生分割振动,因此,本文的结论仅在低频时成立。
参考文献:
[1] 马大猷. 现代声学理论基础[M]. 北京: 科学出版社, 2004: 72-73.
MA Da-you. Basis of modern acoustical theory[M]. Beijing: Science Press, 2004: 72-73.
[2] 杜功焕, 朱哲民, 龚秀芬. 声学基础[M]. 南京: 南京大学出版社, 2001: 116-145.
DU Gong-huan, ZHU Zhe-min, GONG Xiu-fen. Acoustic basis[M]. Nanjing: Nanjing University Press, 2001: 116-145.
[3] 王以真. 实用扬声器技术手册[M]. 北京: 国防工业出版社, 2003: 23-24.
WANG Yi-zhen. Practical speaker technical manual[M]. Beijing: National Defense Industry Press, 2003: 23-24.
[4] 徐光泽. 电声原理与技术[M]. 北京: 电子工业出版社, 2007: 37-39.
XU Guang-ze. Principle and technology of electro-acoustic[M]. Beijing: Electronics Industry Press, 2007: 37-39.
[5] 张平柯. 音频放大器低频性能的短纯音信号评测法研究[J]. 中南大学学报: 自然科学版, 2008, 39(5): 1068-1074.
ZHANG Ping-ke. Evaluation method of low frequency performance of audio frequency amplifiers by tone burst signals[J]. Journal of Central South University: Science and Technology, 2008, 39(5): 1068-1074.
[6] 黎捷. Maple9.0符号处理及应用[M]. 北京: 科学出版社, 2004: 140-144.
LI Jie. Maple9.0 symbol-processing and its applications[M]. Beijing: Science Press, 2004: 140-144.
[7] 王柔怀. 常微分方程讲义[M]. 北京: 人民教育出版社, 1978: 115-122.
WANG Rou-huai. Ordinary differential equations[M]. Beijing: People’s Education Press, 1978: 115-122.
[8] F.S.克劳福德. 波动学(上册)[M]. 卢鹤绂, 译. 北京: 科学出版社, 1981: 121-137.
Crawford F S. Waver(Volume 1)[M]. LU He-fu, trans. Beijing: Science Press, 1981: 121-137.
[9] 万平英. 声频测量技术[M]. 北京: 国防工业出版社, 2006: 77-83.
WAN Ping-ying. Audio measurement technology[M]. Beijing: National Defense Industry Press, 2006: 77-83.
[10] 王以真, 沈伟星. 音箱研讨(三): 扬声器低频参数的测试和计算[J]. 电声技术, 2007, 31(2): 25-29.
WANG Yi-zhen, SHEN Wei-xing. Study and discussion on loudspeakers (Ⅲ): Measurement and calculation of low-frequency parameters of loudspeaker[J]. Audio Engineering, 2007, 31(2): 25-29.
[11] 曹水轩, 沙家正. 扬声器及其系统[M]. 南京: 江苏科学技术出版社, 1991: 133, 373.
CAO Shui-xuan, SHA Jia-zheng. Speaker and its system[M]. Nanjing: Jiangsu Science and Technology Press, 1991: 133, 373.
[12] 叶希鹏. 详解扬声器中品质因数Q值[J]. 电声技术, 2006, 30(8): 26-28.
YE Xi-peng. Analysis of quality factor of loudspeaker[J]. Audio Engineering, 2006, 30(8): 26-28.
[13] 王以真, 沈伟星. 音箱研讨(五): 扬声器的机械Q值Qms[J]. 电声技术, 2007, 31(5): 20-24.
WANG Yi-zhen, SHEN Wei-xing. Study and discussion on loudspeakers (Ⅴ): Mechanical quality factor of the loudspeaker[J]. Audio Engineering, 2007, 31(5): 20-24.
[14] 王以真, 沈伟星. 音箱研讨(二): 论扬声器品质因数Qts [J]. 电声技术, 2006, 30(12): 22-26.
WANG Yi-zhen, SHEN Wei-xing. Study and discussion on loudspeakers (Ⅱ): Analysis of quality factor Qts of loudspeaker[J]. Audio Engineering, 2006, 30(12): 22-26.
[15] 克林格尔. 高保真扬声器和扬声器箱[M]. 沈执良, 钟厚琼, 译. 北京: 科学普及出版社, 1984: 20.
Klinger. High-fidelity speakers and speaker boxes[M]. SHEN Zhi-liang, ZHONG Hou-qiong, trans. Beijing: Popular Science Press, 1984: 20.
(编辑 陈灿华)
收稿日期:2010-01-20;修回日期:2010-03-25
基金项目:湖南省科技计划项目(2009GK3144)
通信作者:张平柯(1956-),男,湖南浏阳人,教授,从事物理学、电声学研究;电话:13907314207;E-mail: zhangpingke@126.com