J. Cent. South Univ. (2016) 23: 1954-1960
DOI: 10.1007/s11771-016-3252-4

Saturation influence of control voltage on maglev stationary self-excited vibration
LI Jin-hui(李金辉)1, 2, LI Jie(李杰)1, YU Pei-chang(余佩倡)1
1. College of Mechatronics Engineering and Automation, National University of Defense Technology,
Changsha 410073, China;
2. The First Engineers Scientific Research Institute of the General Armaments Department, Wuxi 214035, China
 Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Abstract: This work addresses the saturation influence of control voltage on the occurring of self-excited vibration of maglev vehicle-bridge interaction system, which greatly degrades the stability of the levitation control, decreases the ride comfort, and restricts the cost of the whole system. Firstly, the interaction model of vehicle-bridge system is developed. Based on the interaction model, the relationship between the control voltage and vibration frequency is solved. Then, the variation of the effective direct component and fundamental harmonic are discussed. Furthermore, from the perspective of energy transmission between the levitation system and bridge, the principle underlying the self-excited vibration is explored, and the influence on the stability is discussed. Finally, in terms of the variation of the characteristic roots, the influence is analyzed further and some conclusions are obtained. This study provides a theoretical guidance for mastering the self-excited vibration problems.
Key words: maglev; levitation; saturation; self-excited vibration
1 Introduction
Compared with the conventional rail-way systems, the electromagnetic maglev system (EMS) has advantages of lower noise, less exhaust fumes emission, less maintenance cost and the ability to climb steeper slopes, which is a new kind of urban transport that has been widely concerned in recent years [1-3].
The rapid development and enormous advantages of maglev sketch a bright future for its commercial applications. However, the self-excited vibration of bridge is a burning issue to be solved. It occurs when the vehicle is suspended upon the guideway, standing still or moving at very slow speed [4]. It degrades the safety of bridge and durability of bridge. Furthermore, the self-excited vibration deteriorates the stability of the levitation system.
ALBERT et al [5] pointed out that the American Maglev Technologies (AMT) system achieved successful levitation in Florida on a guideway mounted to the earth on a concrete foundation, but later encountered difficulties in achieving stable levitation when the vehicle was moved to an elevated bridge installed on the Old Dominion University campus. It was believed that the flexibility of the bridge, which employed 90-feet length, was the main reason contributed to the difficulties of achieving a stable levitation.
To explore the principle underlying the self-excited vibration and solve the issue, extensive researches have been reported. ZOU et al [6] carried out the derivation of bifurcation equations and numerical simulation using the center manifold method. They believed that the bifurcations, such as the homoclinic, Hopf bifurcation, secondary Hopf bifurcation and chaos, are the causes of self-excited vibration. LI and MENG [7] pointed out that the self-excited vibration is due to the improper frequency relationship between various components of the system. WANG [8] believed that the self-excited vibration is more likely to occur if the difference between the modal frequency of bridge and the natural frequency of controller is sufficiently small. WANG [9], LI [10], ZHANG et al [11] studied the influences of signal delay on the stability of nonlinear levitation system. The analysis shows that, when the time delay reaches a critical value, the system will undergo a sub-critical bifurcation, and the periodic vibration will occur.
However, the saturation influence of control voltage is not considered in all aforementioned researches. It has been observed that the direct component of control voltage shifts with the amplitude variation of vibration when the self-excited oscillation occurs. Besides, the effective alternating component of control voltage may be attenuated due to the limited output amplitude of power system. Hence, the saturation influence of control voltage should be studied extensively.
This work is engineering-oriented, and the purpose of this research is to develop a minimum model that is capable of exploring the principle underlying the self- excited vibration and mastering the saturation influence of control voltage on the stability of the interaction system.
2 Modeling of vehicle-bridge interaction system
Considering the complexity of the self-excited vibration problem, an overall dynamic model of the interaction system with prominent details may result in a complicated analysis to draw useful conclusions, so that a minimum interaction model containing two quintessential parts, a flexible bridge and a single levitation unit, should be developed
2.1 Modeling of bridge
The minimum interaction model is shown in Fig. 1. The variables y0 and y1 are the vertical displacements of bridge and electromagnet, respectively. The variable δ is the levitation gap measured by the gap sensor, and m1 is the equivalent mass of electromagnet.
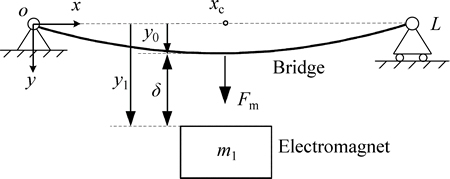
Fig. 1 Minimum model of vehicle-bridge interaction system
The motion of bridge may be described by the following differential equation [1]:
 (1)
(1)
where x is the axial coordinate of the bridge; t is the time; EIb is the bending rigidity; ρb is the mass per unit length; f (x, t) is the electromagnetic force acting on the bridge.
For a simply supported bridge [2], the k-th modal frequency ωk and modal shape functions fk(x) are:
 (2)
(2)
 (3)
(3)
where λk=kπ/L. Using the modal superposition method, the solutions of the equation (1) may be expressed as
 (4)
(4)
where qk(t) is the time-varying amplitude of the k-th modal displacement. Substituting Eq. (4) into Eq. (1), multiplying both sides of the aforementioned resultant equation by sin (nπx/L), and integrating both sides from 0 to L, it gives
 (5)
(5)
Denoting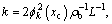 yk(t) and vk(t) are the k-th modal displacement and velocity of bridge, respectively. Multiplying both sides of the resultant equation by fk(xc), it gives
yk(t) and vk(t) are the k-th modal displacement and velocity of bridge, respectively. Multiplying both sides of the resultant equation by fk(xc), it gives
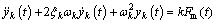 (6)
(6)
Therefore,
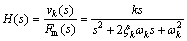 (7)
(7)
Equation (7) may be considered the response of vertical velocity of bridge roused by the electromagnetic force.
2.2 Modeling of levitation system
Suppose that the turn of a single electromagnet is N, the pole area is A and the magnetic permeability of vacuum is μ0. Then for a single electromagnet, the relationship between the controlled voltage u (t) and current i (t) is [3]:
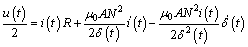 (8)
(8)
where R is the DC resistance; the levitation gap is  The electromagnetic force Fm(t) acting on the bridge is [4]:
The electromagnetic force Fm(t) acting on the bridge is [4]:
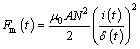 (9)
(9)
Considering the isolation effect of air springs, the dynamics of sprung mass is neglected here, then
 (10)
(10)
where g is the acceleration of gravity; M1 is the sprung mass. According to Eqs. (8)-(10), the steady voltage of the electromagnet is
 (11)
(11)
Here the variable δ0 is the desired levitation gap. The EMS maglev system uses electromagnetic attractive forces to neutralize the gravity of the train. Unfortunately, the electromagnetic forces produced by a constant current are inversely proportional to the square of the levitation gap, which makes the electromagnetic levitation system inherently unstable, and an active controller is required to stabilize the levitation system around a desired suspension gap.
Recently, the extensive and in-depth studies for levitation system are carried out to achieve satisfactory performance specifications [12-13]. However, the integral-type PD control still is the most widely used control scheme in engineering practice. To explore the principle underlying the self-excited vibration, the integral-type PD control is adopted in this study, which gives
 (12)
(12)
where ie(t) is the desired current through the electromagnet; kp and kd are the parameters of PD controller. To accelerating the response of the actuator, a cascaded current controller is used [14-15]:
 (13)
(13)
The resistance of electromagnet shares a part of control voltage, which results in a steady error between the expected and actual current of the coils. To remove it, a current feed forward control strategy is proposed. Then,
 (14)
(14)
Hence, the total control voltage of levitation system is
 (15)
(15)
Considering that the output limitation range of power system on-board is [-AmAm], then
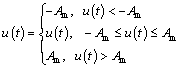 (16)
(16)
The motion of the levitation system is determined by Eqs. (8)-(16). To here, the minimum interaction model has been developed.
3 Saturation influence of control voltage
It has been observed that the self-excited vibration occurs when the vehicle is suspended upon the guideway, standing still or moving at very slow speed [4]. When the speed of vehicle is larger than 10 km/s approximately, during the period of the vehicle passing over a beam, the energy accumulated by the bridge is limited, and the vibration amplitude of the bridge is sufficiently small that can not be observed. Hence, in the present study, the vehicle is assumed to be standing still without moving. In this situation, the crossing of the vehicle between the joints of the beams is not considered.
3.1 Solving of control voltage
When the vibration amplitude of the bridge is sufficiently small, the interaction system is quasi-static, so that the linearized model may be applied to explore the influence of control voltage on the stability of self- excited vibration without introducing noticeable errors. When without consideration of the saturation influences of the control voltage, the linearized motion equations in frequency domain are

 (17)
(17)
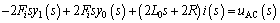 (18)
(18)
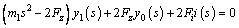 (19)
(19)
According to Eqs. (17)-(19), there are four variables in three equations. Here the transfer function between two variables may be solved. Defining 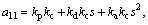
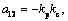



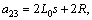
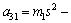

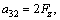
 then Eqs. (17)-(19) are translated into the following augmented matrix:
then Eqs. (17)-(19) are translated into the following augmented matrix:
 (20)
(20)
Then, the transfer functions between the control voltage and the displacements of electromagnet and bridge are
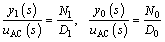 (21)
(21)
where

 D1=
D1=

Then,
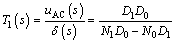 (22)
(22)
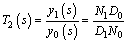 (23)
(23)
It has been observed that the levitation system will be unstable when the fluctuation of the levitation gap is greater than 5 mm. Hence, on the presumption that the fluctuation amplitude of the levitation gap is 5 mm, the relationships between the vibration frequency ωVib and control voltages are shown in Fig. 2.
According to Fig. 2, when the vibration frequency is less than 30 rad/s, the alternating component of control voltage uAC is slowly varying. With the increment of vibration frequency, uAC is changed jumpy, which is mainly due to the phase error between the displacement of bridge and electromagnet, which is shown in Fig. 3. Furthermore, when the vibration frequency is greater than 200 rad/s, which is beyond the traceability range of levitation system, the displacement and velocity of electromagnet are insignificant. In this situation, the alternating component of control voltage is mainly determined by the motional states of bridge, which tends to be a constant value, as shown in Fig. 3.
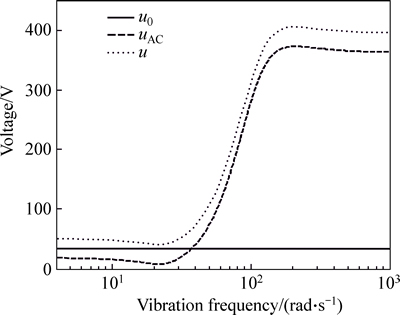
Fig. 2 Relationship between vibration frequency and control voltage

Fig. 3 Bode diagrams between displacement of bridge and electromagnet
For the CMS04 low-speed maglev system, the maximum output of power system is 330 V. According to Fig. 2, the control voltage is up to 400 V. Hence, the control voltage will be limited by the output of power system.
3.2 Analysis of saturation
When the control voltage u is greater than the maximum output Am of power system, it can be classified into two situations. The first one is the single terminal saturation situation, which gives
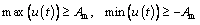 (24)
(24)
The second one is the double terminals saturation situation, which gives
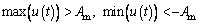 (25)
(25)
The character of the first situation is shown in Fig. 4.

Fig. 4 Single terminal saturation of control voltage
When the upper of control voltage is limited, the effective direct component of u will be less than u0. However, due to the integration feedback of levitation gap error, the effective direct component will run to a new equilibrium point, and the value of interception between the updated control voltage and imaginary axis will be greater than u0 , which is noted as and shown in Fig. 4. According to Fig. 4, it gives
and shown in Fig. 4. According to Fig. 4, it gives
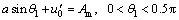 (26)
(26)
 (27)
(27)
The updated control voltage u is
 (28)
(28)
Its direct component satisfies the following equation.
 (29)
(29)
Apart from the variation of the direct component, the saturation of control voltage has an effect on its harmonic component. For the self-excited vibration, the variation of fundamental harmonic should be considered extensively. Denoting the fundamental harmonic as 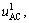 and the amplitude of uAC as a, then,
and the amplitude of uAC as a, then,
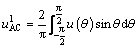
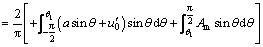 (30)
(30)
Furthermore, the character of the second saturation situation is shown in Fig. 5.
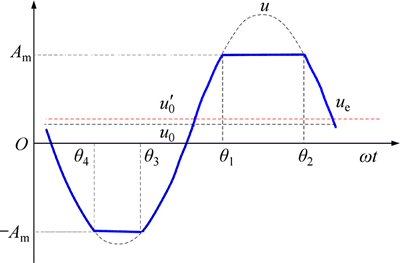
Fig. 5 Double terminals saturation of control voltage
The variation of direct component and fundamental harmonic of the double terminals saturation situation can be solved with the similar methods, which are omitted here.
When δ0=0.009, N=360, R=0.55, A=0.0184, kp=5000, kd=40, ka=0.4, kc=40, the relationships between control voltages and vibration frequency are shown in Fig. 6.
According to Fig. 6, When the vibration frequency is less than 90 rad/s, the control voltage u is less than Am. In this situation,  is equal to u0. With the increment of vibration frequency, the control voltage is limited, and
is equal to u0. With the increment of vibration frequency, the control voltage is limited, and  is increasing. Besides, the control voltage u is increasing with the vibration frequency all the time. For its fundamental harmonic
is increasing. Besides, the control voltage u is increasing with the vibration frequency all the time. For its fundamental harmonic 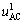 , the maximum value is 348.6 V when the vibration frequency is 106.2 rad/s. With the increment of vibration frequency, the double terminals of control voltage are limited, and the fundamental harmonic
, the maximum value is 348.6 V when the vibration frequency is 106.2 rad/s. With the increment of vibration frequency, the double terminals of control voltage are limited, and the fundamental harmonic 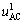 decreases although the control voltage is increasing.
decreases although the control voltage is increasing.
To study the influences of fundamental harmonic 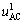 , the scale factor β is denoted as
, the scale factor β is denoted as
 (31)
(31)
Then, the relationship between scale factor β and vibration frequency is shown in Fig. 7.

Fig. 6 Relationships between control voltages and vibration frequency:
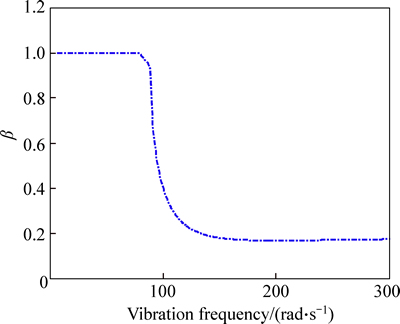
Fig. 7 Relationship between scale factor and vibration frequency
3.3 Influences analysis based on levitation model
To study the influence of saturation, Eq. (14) can be translated into Eq. (32) when the self-excited vibration occurs at the frequency ωVib.
 (32)
(32)
Furthermore, the dynamic equations of levitation system may be rewritten as
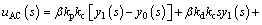
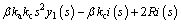 (33)
(33)
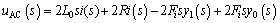 (34)
(34)
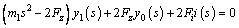 (35)
(35)
The intuitive characteristic of self-excited oscillation is the vertical vibration of bridge with a single frequency sinusoidal wave, and the main factor determining the vibration amplitude increment of bridge is the electromagnetic force acting on the bridge. Hence, from the perspective of energy transmission between the levitation system and bridge, the influence of saturation may be explored clearly. When denoting a11=2Fzs, a12=-2Fis, a13=s, b1=2Fz, a21=m1s2, 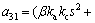
 a32=-(2L0s+βkc)s, b3=(2Fis+ βkpkc),
a32=-(2L0s+βkc)s, b3=(2Fis+ βkpkc),
 (36)
(36)
To explore the influence of saturation in terms of energy transmission quantitatively, the vibration frequency is assumed as ωVib and the velocity of bridge is defined as In light of Eq. (36), the electromagnetic force acting on the bridge is
In light of Eq. (36), the electromagnetic force acting on the bridge is
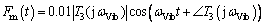 (37)
(37)
Then, the averaged power of the electromagnetic force acting on the bridge is
 (38)
(38)
According to Fig. 8, when the saturation of control voltage is not considered and the vibration frequency is less than ωC (zero-axial frequency), the vibration energy will flow into levitation system. Considering the passivity of bridge, its amplitude of vibration will decay to zero. Hence, the frequency range [0 ωC] is stable.
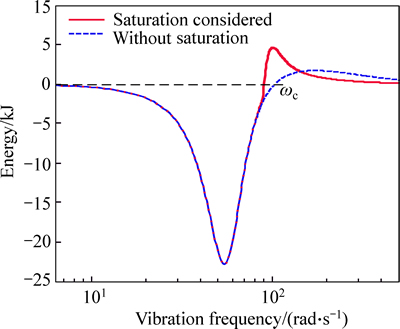
Fig. 8 Energy transmission between levitation system and bridge
On the contrary, when the vibration frequency is greater than ωC, the levitation system will export energy to bridge. If the power dissipated by the modal damping of bridge is less than the exported power by the levitation system, the self-excited vibration may occur. Hence, the frequency range [ωC ∞] may be unstable.
When the saturation of control voltage is considered, the stable frequency range is suppressed, and the maximum power flowing to bridge is up to 5 kJ when the vibration frequency is 100 rad/s, which is much greater than the maximum power 2 kJ when the saturation of control voltage is not considered. Hence, from the perspective of energy transmission, the saturation of control voltage is harmful for the stability of interaction system between [90 143] rad/s.
Conversely, we can conclude that the saturation of control voltage is beneficial to the suppression of self- excited vibration when the frequency is larger than 143 rad/s.
3.4 Influence analysis based on vehicle-bridge interaction system
From the perspective of energy transmission, the influence of control voltage on the stability of self-excited vibration has been studied based on the levitation model. However, in above section, the characters of bridge are not considered.
To study the saturation influence of control voltage more comprehensive, the model of vehicle-bridge interaction system will be adopted in this section.
It has been observed that the bridge vibrates vertically when the self-excited vibration occurs. With the passage of time, the amplitude of vibration increases until the failure of the levitation system or a self- oscillation with constant amplitude. To some extent, the fluctuation of the levitation gap is the main markers of self-excited vibration. Therefore, the transfer function between the levitation gap δ(t) and desired levitation gap δ0(t) is creditable to judge the stability of the interaction system.
When the voltage saturation influence is considered, combing Eqs. (6), (33)-(35), the transfer function between δ(s) and δ0(s) is solved.
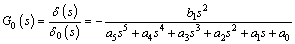 (39)
(39)
For Eq. (39), b1= a5=2L0m1, a4=
a5=2L0m1, a4=  a3=2kdβkcFi+2βkcξωm1+2L0m1ω2, a2=
a3=2kdβkcFi+2βkcξωm1+2L0m1ω2, a2=
2kpβkcFi+βkcm1ω2+4kdβkcFiξω+2km1βkckpFi-2km1βkcFz-2βkcFz, a1=-4ξωβkcFz+2kdβkcFiω2.
When ξ=0.01, L=18, ρb=1000, there are five characteristic roots for G0(s), including one negative number with zero imaginary part, which is mainly corresponding to the current loop of levitation system (blue), one pair of conjugation poles which is mainly corresponding to the traceability of levitation system and shown in the left of Fig. 9 (black), one pair of conjugation pole which is mainly corresponding to the traceability, and one pair of conjugation poles which is mainly corresponding to the character of bridge (red). In Fig. 9(a), the modal frequency of bridge is 60 rad/s. In Fig. 9(b), it is 180 rad/s.

Fig. 9 Variation of characteristic roots when saturation of control voltage is considered:
When the saturation of control voltage is not considered, the characteristic roots of Eq. (39) are mapped in Fig. 9 with the mark of “o”. It can be observed that the interaction system will be stable for the bridge whose modal frequency is 60 rad/s and unstable for the bridge whose modal frequency is 180 rad/s. In this sense, the modal frequency of bridge has a noticeable effect on the stability of the interaction system.
When considering the saturation of control voltage, the real parts of the three characteristic roots (blue and black), which are mainly corresponding to the stability of levitation system itself, are increasing. In this sense, the saturation of control voltage is harmful for the stability of levitation system itself. As for the characteristic roots (red), which are mainly corresponding to the vibration of bridge, the saturation of the control voltage is harmful for the stability of bridges whose modal frequency is 60 rad/s, and beneficial for the stability of bridges whose modal frequency is 180 rad/s. It enhances the validity of the conclusions obtained in the above section.
4 Conclusions
1) The interaction model of vehicle-bridge system with active control has been developed. Based on the model, the relationship between the control voltage and vibration frequency is solved.
2) The variation of the effective control voltage due to the saturation, including the direct component and fundamental harmonic is obtained
3) The saturation of control voltage is harmful for the stability of interaction system between [90 143] rad/s, and beneficial to the suppression of self-excited vibration when the frequency is larger than 143 rad/s.
References
[1] ELVIN N G, ELVIN A A A. An experimentally validated electromagnetic energy harvester [J]. J Sound Vib, 2011, 330(5): 2314-2324.
[2] ZHOU D F, HANSEN C H, LI J. Suppression of maglev vehicle-girder self-excited vibration using a virtual tuned mass damper [J]. J Sound Vib, 2011, 330(5): 883-901.
[3] WAI R J, LEE J D, CHUANG K L. Real-time PID control strategy for maglev transportation system via particle swarm optimization [J]. IEEE Trans Ind Electron, 2011, 58(2): 629-646.
[4] ZHOU D F, HANSEN C H, LI J. Review of coupled vibration problems in EMS maglev vehicle [J]. J Vib Acoust, 2010, 15(1): 10-23.
[5] ALBERT T E, OLESZCZUK G, HANASOGE A M. Stable levitation control of magnetically suspended vehicles with structural flexibility [C]// Proceedings of the 2008 American Control Conference. Washington, 2008: 4035-4040.
[6] ZOU D S, SHE L H, ZHANG Z Q, ZHOU F M. Maglev vehicle and guideway coupling vibration analysis [J]. Acta Electronica Sinica, 2010, 38(9): 2071-2075.
[7] LI L, MENG G. The analysis of coupling vibration between maglev vehicle and steel bridge [J]. Journal of Vibration and Shock, 2006, 25(6): 46-75.
[8] WANG H P, LI J, ZHANG K. Vibration analysis of the maglev guideway with the moving load [J]. J Sound Vib, 2007, 305(4): 621-640.
[9] WANG H P, LI J, ZHANG K. Sup-resonant response of a nonautonomous maglev system with delayed acceleration feedback control [J]. IEEE Trans Magn, 2008, 44(10): 2338-2350.
[10] LI X L, ZHANG L L, ZHANG Z Z, SHE L H, HUANG L H. Bifurcation control for maglev system with two state feedback delays [C]// Proceeding of the 2008 IEEE International Conference on Information and Automation. 2008: 244-247.
[11] ZHANG Z Z, ZHANG L L. Hopf bifurcation of time-delayed feedback control for maglev system with flexible guideway [J]. Applied Mathematics and Computation, 2013, 219(11): 6106-6112.
[12] LI Y G, ZHANG D, CHENG H. The design and simulation of an adaptive maglev control algorithm based on oscillation observation [C]// Proceedings of the 18th International Conference on Magnetically Levitated Systems and Linear Drives. 2004: 984-990.
[13] KONG E, SONG J S, KANG B B. Dynamic response and robust control of coupled maglev vehicle and guideway system [J]. J Sound Vib, 2011, 330(25): 6237-6253.
[14] LI Y G, CHANG W S. Cascade control of an EMS maglev vehicle’s levitation control system [J]. Acta Automatica Sinica, 1999, 25(2): 247-251.
[15] GUZMAN H. Current loops in a magnetic levitation system [J]. Journal of Innovative Computing, Information and Control, 2004, 5(5): 1275-1283.
(Edited by YANG Hua)
Foundation item: Projects(11302252, 11202230) supported by the National Natural Science Foundation of China
Received date: 2015-03-04; Accepted date: 2016-01-18
Corresponding author: LI Jin-hui, PhD; Tel: +86-731-84573387; E-mail: li_jinhui@126.com