DOI: 10.11817/j.issn.1672-7207.2015.12.035

随机卸荷岩体裂纹流变断裂模型与数值模拟

赵延林^{1, 2}，曹平³，万文¹，张英⁴，唐劲舟¹，王卫军¹

(1. 湖南科技大学 能源与安全工程学院，煤矿安全开采技术湖南省重点实验室，湖南 湘潭，411201；

2. 中国矿业大学 煤炭资源与安全开采国家重点实验室，江苏 徐州，221008；

3. 中南大学 资源与安全工程学院，湖南 长沙，410083；

4. 重庆地质矿产研究院，外生成矿与矿山环境重庆市重点实验室，重庆，400042)

摘要：针对卸荷裂纹发生的随机性，发生时间的滞后性特点，采用岩石断裂力学和流变力学，结合Monte-Carlo方法描述岩体裂纹的随机分布，研究随机卸荷裂纹扩展的时效特性，建立随机卸荷岩体裂纹流变断裂模型及数值方法，并提出卸荷岩体裂纹止裂判据。以最小应力σ₃卸荷为例，探索不同卸荷条件下，随机卸荷裂纹的萌生、流变扩展规律。研究结果表明：随着最小应力σ₃的卸荷，岩体裂纹瞬态扩展和流变扩展都增强；最小主应力接近     0 MPa时，对最小主应力较小的扰动变化，将导致卸荷裂纹的成倍增加。卸荷岩体裂纹的流变断裂与岩石流变过程相似，呈现出衰减流变阶段和定常流变阶段2个阶段。随机卸荷岩体裂纹流变断裂模型合理地解释了岩体裂纹的延迟起裂、流变扩展和止裂，为研究卸荷岩体变形损伤特性提供了细观层面上的理论依据。

关键词：岩石力学；卸荷岩体；岩体裂纹；流变断裂

中图分类号：TU452             文献标志码：A         文章编号：1672-7207(2015)12-4647-10

Model and numerical simulation of rheological fracture of random unloading rock mass cracks

ZHAO Yanlin^{1, 2}, CAO Ping³, WAN Wen¹, ZHANG Ying⁴, TANG Jinzhou¹, WANG Weijun¹

(1. Hunan Provincial Key Laboratory of Safe Mining Techniques of Coal Mines,

School of Energy and Safety Engineering, Hunan University of Science and Technology, Xiangtan 411201, China;

2. State Key Laboratory of Coal Resources and Safety Mining,

China University of Mining and Technology, Xuzhou 221008, China;

3. School of Resources and Safety Engineering, Central South University, Changsha 410083, China,

4. Chongqing Key Laboratory of Exogenic Mineralization and Mine Environment,

Chongqing Institute of Geology and Mineral Resources, Chongqing 400042, China)

Abstract: According to the randomness of occurrence and the hysteretic nature of occurrence time of unloading cracks, the rock fracture mechanics and rheological mechanics were adopted to study the aging characteristics of random unloading cracks extension. Based on random distribution of rock cracks depicted by Monte-Carlo method, the rheological fracture model of random unloading rock mass cracks and numerical simulation were established, and criterion of unloading cracks arrest was also proposed. Taking unloading of the minimum principal stress as an example,the initiation and rheological extension laws of random unloading cracks were explored. The results show that the transient cracks extension and rheological cracks extension are strengthened because of unloading of the minimum principal stress. When the minimum principal stress is close to 0 MPa, small disturbance to the minimum principle stress will give rise to double increasing of unloading cracks. The rheological fracture process of unloading rock mass cracks is similar to that of rocks, and rheological fracture of rock cracks indicates attenuating rheological stage and steady rheological stage. The rheological fracture model of random unloading rock mass cracks reasonably explains the delay cracks initiation, rheological extension and cracks arrest of rock mass, which provides microscopic theory basis for deformation damage of unloading rock mass.

Key words: rock mechanics; unloading rock mass; rock mass cracks; rheological fracture

岩体由于卸除一向或二向荷载而引起的承载能力降低的现象为岩体卸荷破坏^[1-3]。卸荷岩体力学是岩石力学研究的新领域，它是研究自然界卸荷岩体在力及其他因素作用下的岩体力学性质及其工程应用的科学。自提出卸荷岩体力学概念并建立卸荷岩体力学理论体系以来，卸荷岩体力学理论得到了众多学者的关注。我国开始重视岩体开挖卸荷效应方面的研究，其中一个重要的工程背景是三峡工程永久船闸岩石高边坡开挖卸荷变形控制的难题^[4-5]。不少研究者对卸荷岩体的力学试验和强度理论等进行了深入的研究^[6-10]。沈军辉等^[11]通过三轴卸荷岩体破坏试验得出岩体在卸荷状态下的变形表现为沿卸荷方向的强烈扩容，其破裂以张性破裂为特征。周小平等^[12]研究了峰前围压卸荷条件下岩石的应力-应变全过程，得到了围压卸荷下岩石变形局部化规律。在进行大量的卸荷试验的同时，岩体卸荷理论的研究也逐步发展起来。哈秋舲^[4]针对三峡工程永久船闸，应用系统工程原理和方法组织多学科研究，使地质学、非线性力学、工程学和监测技术融为一体，提出了卸荷非线性岩体力学。李建林等^[13]考虑边坡各向异性地质特征和边坡力学动态条件，采用模拟试验、数值计算、岩体分类和物探等方法，建立了各向异性卸荷非线性关系。但由于岩体卸荷破坏机制的复杂性，已有的成果多局限于岩石力学试验及卸荷理论的初步探讨，而对岩体卸荷裂纹的萌生扩展的理论研究与数值模拟没有深入。岩体在长期地质因素作用下所生成的不同类型的节理、裂纹及软弱界面，使岩体成为不连续、非均匀、各向异性的介质体。岩体的破坏机制、强度和变形特性在很大程度上受这些不连续面的规模、密度及空间分布特性所影响^[14-15]。岩体在开挖卸荷过程中，边界条件处于动态变化中，岩体的力学参数随之不断变化，岩体卸荷过程中诱生的卸荷裂纹也随之动态扩展。岩体卸荷的破坏本质上是卸荷裂纹萌生、聚集和贯通。陶振宇等^[16]认为，这种现象诱生的卸荷裂纹有3个重要的特点：发生卸荷裂纹的随机性；方向大体平行于开挖的临空面的定向性；发生时间的滞后性。岩体具有黏滞性，其破坏过程是渐进的，表现出明显的时间滞后性。从理论上描述岩体的卸荷破坏必须从岩体的流变及卸荷的时效2方面来进行。本文作者采用岩石断裂力学理论，结合流变力学，研究卸荷状态下岩体裂纹断裂扩展的时效特性，即卸荷裂纹发展的时间滞后性。通过构建随机岩体裂纹模型，以最小主应力σ₃卸荷为例，探索不同卸荷条件下，随机卸荷裂纹的萌生、流变断裂规律以揭示工程卸荷岩体破坏失稳的流变力学机理。

1  卸荷岩体裂纹流变断裂模型

一般情况下(不考虑地质构造运动)，处于原岩初始应力状态下，岩体断续裂纹不会扩展，岩体处于自平衡状态。由于开挖卸荷导致围岩的最小主应力得到不同程度释放。在最小主应力卸荷条件下，卸荷裂纹在原生裂纹端部产生，卸荷张拉裂纹流变扩展、贯通，而导致岩体渐进破坏。

1.1  岩体裂纹瞬态起裂

荷载作用下，岩体裂纹尖端应力强度因子K_I大于岩石断裂韧度K_IC时，在裂纹尖端会发生拐折起裂而产生翼形裂纹。

大量试验结果和理论计算^[17-18]表明：压剪裂纹近似垂直于最大拉应力方向开裂，按I型扩展，如图1所示。

裂纹面上传递的法向和切向应力分别为(取压应力为正)：

         

              

                 

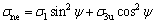
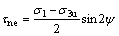
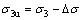
式中：σ_ne和τ_ne分别为裂纹面上的法向应力和切向应力；σ₁为最大主应力；σ₃为最小主应力；σ_3u为卸荷后的最小主应力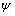；为裂纹面和最大主应力方向的夹角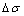；为最小主应力σ₃的卸荷量。

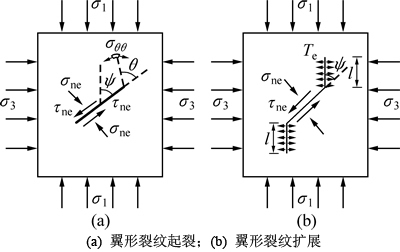
图1  压剪应力状态下翼形裂纹起裂及扩展示意图

Fig. 1  Sketch of wing cracks seeding and propagation in compressive-shear stress state

根据最大周向正应力理论，初始裂纹沿周向最大正应力方向扩展，可求得开裂角θ=70.5^o，翼形裂纹尖端应力强度因子为：

  

       

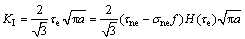
式中：μ为裂纹面的摩擦因数；a为裂纹迹长。

当K_I≥K_IC时压剪裂纹瞬态起裂。

1.2  岩体裂纹延迟起裂

大量研究^[19-20]表明在岩体裂纹存在延迟起裂的力学特性，当裂纹尖端应力强度因子K_I满足式时，裂纹发生延迟起裂。

               

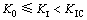
式中：K₀为岩体裂纹亚临界扩展应力强度门槛值，由岩石双扭断裂试件测试得到^[19]。

参考文献[19]，黏弹性压剪裂纹的时间相依应力强度因子K_I(t)为

               

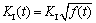
用Burgers模型来描述黏弹性岩石材料，由黏弹对应性原理，对于给定载荷情况下f(t)的关系式为^[19]：

           

              

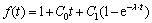
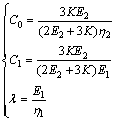
式中：C₀，C₁和λ均为常数，K，E₁，E₂，η₁，η₂分别由岩石试件的蠕变试验得到。

由式可知：当压剪裂纹尖端应力强度因子满足式时，黏弹性压剪裂纹应力强度因子随时间而增加，当K_I(t)=K_IC时，裂纹延迟起裂。

1.3  最小主应力卸荷至零时的应力强度因子

岩体裂纹起裂后开始翼形扩展，随着最小主应力的卸荷, 翼形裂纹近似平行于最大主应力的方向扩展如图2所示。将图2(a)所示的翼形裂纹系统等效为图2(b)所示的等效直裂纹系统。

翼形裂纹尖端应力强度因子K_I(l)由有效剪切驱动力τ_e产生的应力强度因子(K_I)₁、远场最小主应力σ_3u产生的应力强度因子(K_I)₂组成(取压应力为正)：

 

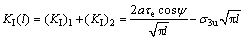
式中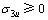：；l为翼形裂纹扩展长度。

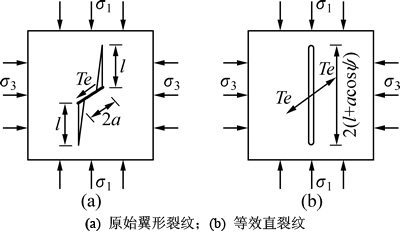
图2  压剪状态下翼形裂纹等效示意图

Fig. 2  Sketch of wing branch cracks and equivalent crack in compressive-shear stress state

1.4  最小主应力卸荷至拉应力时的应力强度因子

当最小主应力卸荷至拉应力时，一部分原生裂纹要张开，由式得

           

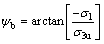
当原生裂纹的倾角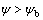时，裂纹张开，裂纹处于拉剪状态；当原生裂纹的倾角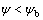时，裂纹闭合，裂纹处于压剪状态。

拉剪状态的裂纹下，原生裂纹尖端应力强度因子为

   

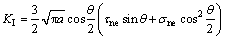
将式(3)对θ求偏导数并令其等于0，即可得到裂纹的开裂角θ₀满足的关系式

    

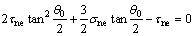
拉剪应力状态下在卸荷裂纹起裂方向上的应力强度因子为

  

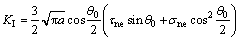
当K_I≥K_IC时，岩体裂纹在拉剪应力作用下扩展，扩展中翼形裂纹尖端应力强度因子K_I(l)为^[21]

 

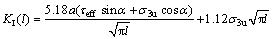
1.5  考虑裂纹之间相互作用的应力强度因子

考虑裂纹之间的相互作用，根据Ashby等^[22]的相关研究，引入多裂纹之间的相互作用所起的附加应力强度因子K_I(ρ)为

  

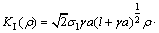
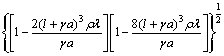
式中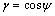：；ρ为裂纹面密度，ρ=1/S，S为优势裂纹面的间距平均值；λ为侧压系数，λ=σ₃/σ₁。

卸荷岩体翼形裂纹尖端的应力强度因子K_I由K_I(l)和K_I(ρ)叠加而成，即有：

           

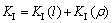
对于压剪裂纹，K_I(l)采用式；对于拉剪裂纹，K_I(l)采用式。

1.6  翼形裂纹流变断裂

实验研究表明当裂纹尖端应力强度因子K_I在岩石断裂韧度K_IC和岩石的亚临界裂纹扩展门槛值K₀之间，即K₀≤K_I≤K_IC时，裂纹进入亚临界扩展阶段^[23]。裂纹发生流变断裂。

对于压剪断裂，随翼形裂纹扩展，裂纹尖端的应力强度因子不断衰减，在式中，令K_I=K_IC，得到翼形裂纹瞬态扩展长度l₁。当翼形裂纹尖端应力强度因子K_I满足K₀≤K_I≤K_IC时，翼形裂纹扩展进入流变断裂阶段。当翼形裂纹尖端应力强度因子K_I≤K₀时，裂纹停止扩展。在式中，令K_I=K₀，得到翼形裂纹最终扩展长度l_n，则翼形裂纹流变扩展长度为l₂=l_n-l₁。图3为翼形裂纹瞬态起裂扩展长度l₁和流变扩展长度l₂计算示意图。

对于拉剪断裂，裂纹尖端应力强度因子由式和确定，由式得，在裂纹扩展的有限长度内，裂纹扩展长度是应力强度因子的单调增函数，裂纹的继续扩展不需要增加应力，裂纹扩展是失稳扩展。最小主应力卸荷至拉应力时，拉剪裂纹不存在流变断裂扩展效应，裂纹瞬态扩展失稳，与其他裂纹贯通后止裂。

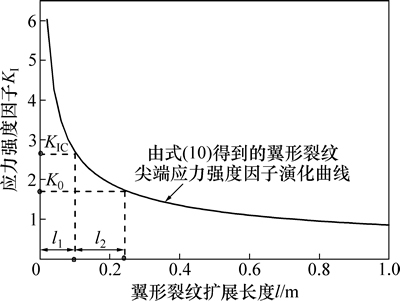
图3  翼形裂纹瞬态起裂扩展和流变扩展计算示意图

Fig. 3  Calculation sketch of instantaneous propagation and rheologic propagation

岩石裂纹的亚临界扩展实验研究发现，岩体裂纹流变断裂扩展的速率可用下式表示^{[19, 23]}：

    

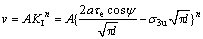
式中：l取裂纹瞬态扩展长度l₁和最终扩展长度l_n之间任意值。由式可得到翼形裂纹流变断裂过程中，不同扩展长度的瞬态扩展速率。

从式(18)可以看出：随翼形裂纹的流变断裂，裂纹亚临界扩展速率越来越小。当翼形裂纹扩展至尖端应力强度因子为亚临界裂纹扩展门槛值时，裂纹流变扩展的速率极低，可以认为翼形裂纹止裂。

2  卸荷状态下岩石单裂纹流变断裂分析

2.1  岩石单裂纹流变断裂分析

岩石单裂纹流变断裂分析的实现过程如下：

1) 在式中令K_I=K_IC和K_I=K₀，得到裂纹的瞬态起裂扩展长度l₁、最终扩展长度l_n和流变扩展长度l₂=l_n-l₁。

2) 将翼形裂纹流变扩展长度l₂离散成n个子单元，得到各子单元的翼形裂纹扩展长度△l_i，由式得到各个子单元段的流变扩展(亚临界扩展)速率v_i，则每个子单元的流变扩展时间△t_i为

              

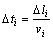
3) 累加各子单元的流变扩展时间得到翼形裂纹流变扩展总时间t=△t₁+△t₂+…+△t_n。

2.2  算例

利用理论模型研究不同卸荷条件下岩石单裂纹的流变断裂特性。岩石裂纹结构的计算参数如下：岩体裂纹长度2a=1.31 m；裂纹和最大主应力方向的夹角φ=52°；裂纹面的摩擦因数f=0.3。图4所示为翼形裂纹流变断裂计算单元示意图。

选取3种不同卸荷状态研究单一裂纹的流变断裂：1) σ₁=20 MPa，σ₃=4.0 MPa；2) σ₁=20 MPa，σ₃= 20 MPa；3) σ₁=20 MPa，σ₃=0 MPa。

图5所示为不同卸荷状态下，翼形裂纹流变断裂曲线。从图5可以看出：随时间的延长，裂纹扩展长度增长。与岩石流变过程相似，岩体裂纹流变断裂也呈现出衰减流变阶段、定常流变阶段，在岩体裂纹流变断裂的衰减阶段，裂纹扩展速率渐缓；在定常阶段，裂纹扩展速率稳定。当裂纹尖端应力强度因子K_I小于岩体裂纹亚临界扩展应力强度因子K₀，裂纹扩展停止。岩体裂纹流变断裂与岩石流变过程相似的本质原因在于：随裂纹流变扩展，裂纹尖端应力强度因子不断衰减，由式(18)可知裂纹流变扩展速率非线性减少，岩体裂纹流变断裂呈现出衰减流变特性。由图3可知：随着裂纹的进一步扩展，裂纹尖端应力强度因子衰减速率渐缓，岩体裂纹流变断裂进入定常流变阶段。

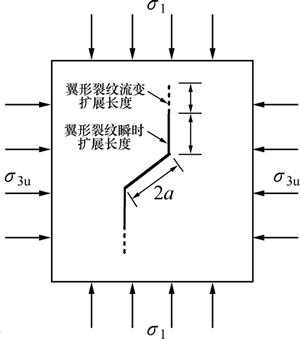
图4  翼形裂纹流变断裂计算单元示意图

Fig. 4  Calculation unit sketch of wing cracks propagation

随着最小主应力σ₃的卸荷，卸荷裂纹瞬态扩展和流变扩展都增强，当最小主应力分别卸荷至0.2σ₁，0.1σ₁和0 MPa时，裂纹瞬态扩展长度分别为0.102，0.224和0.791 m，其流变扩展分别为0.031，0.192和0.830 m。裂纹流变扩展持续时间分别为2.91，20.14和816.02 h。卸载至0 MPa的流变扩展长度远大于最小主应力卸荷至0.2σ₁和0.1σ₁的扩展长度，因而导致前者流变断裂时间远大于后者流变断裂时间。

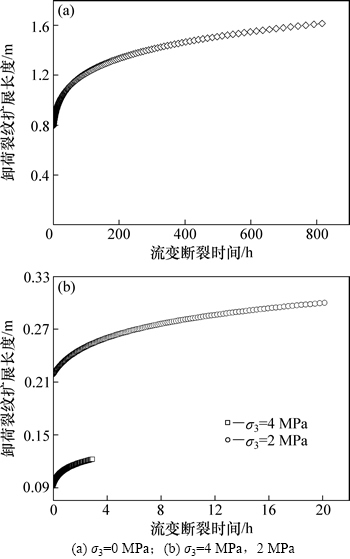
图5  岩体裂纹流变断裂曲线

Fig. 5  Rheological fracture curves of rock mass crack

3  随机卸荷岩体裂纹流变断裂分析

3.1  卸荷岩体裂纹流变断裂程序设计

工程岩体原生裂纹分布十分复杂， 用人为调查方法无法描述岩体系统内真实裂纹的展布，裂纹分布的不确定性与复杂性是导致岩体具强烈各向异性的本质原因。用Monte-Carlo 模拟技术生成岩体随机裂纹网络是研究工程岩体各向异性的好方法。首先，进行野外岩体露头的裂纹测量，包括裂纹间距、隙宽、迹长、倾向和倾角等；其次，求裂纹几何要素的概率密度分布函数关系；最后，采用Monte-Carlo方法模拟从已知概率分布中的随机抽样实现，模拟出比较结合实际的裂纹网络系统。

为研究工程岩体在卸荷条件下裂纹萌生、扩展规律，用Fortran语言开发出基于Monte-Carlo的随机裂纹网络程序，同时根据式~开发不同卸荷状态下卸荷裂纹流变断裂可视化程序。程序中裂纹止裂的判据：1) 裂纹尖端应力强度因子K_I＜K₀，裂纹止裂；2) 翼形裂纹与原生裂纹贯通，裂纹止裂。其程序流程图见图6。

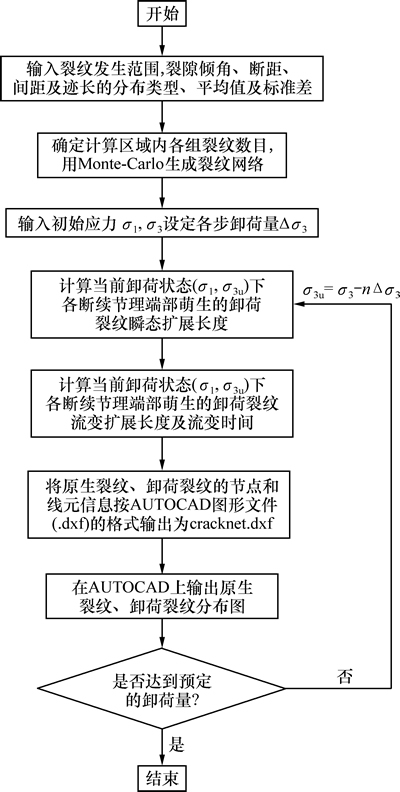
图6  随机卸荷裂纹流变断裂分析流程图

Fig. 6  Rheological fracture flow diagram of random unloading crack

3.2  工程应用

以金川二矿区的1098分段23行的二辉橄榄围岩部分区段为研究对象，通过对现场的地质调查，并对研究区域内节理统计分类后得到的几何参数概率分布参数见表1，用Monte-Carlo模拟得到岩体裂纹网络。图7所示为取样范围内原生裂纹网络与最小主应力σ₃卸荷力学边界示意图，图中，σ_3u=σ₃-n△σ₃(n为卸荷数)。计算区域长×宽为20 m×20 m；初始应力状态σ₁=σ₃=20 MPa，各步卸荷量△σ₃=0.1σ₃。

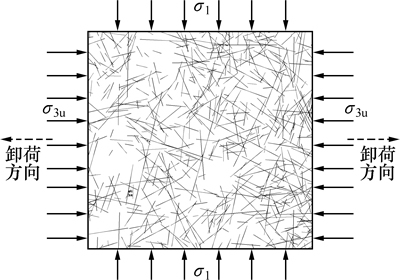
图7  岩体裂纹网络与最小主应力卸荷力学边界示意图

Fig. 7  Sketch of rock mass crack net and unloading mechanical boundary of minimum principle stress

通过对金川二矿区的1098分段23行的二辉橄榄岩双扭试件进行断裂韧度、亚临界扩展的测试得到该处二辉橄榄岩的断裂韧度K_IC=3.41 MPa·m^0.5， 亚临界扩展门槛值K₀=2.50 MPa·m^0.5，岩石裂纹流变断裂扩展速率表达式中A=10^-15.86，n=12.58；岩体裂纹内摩擦因数f=0.3。

流变力学参数通过二辉橄榄岩试件的流变试验得到^[24]。二辉橄榄岩试件的Burgers模型参数见表2。

通过调用随机卸荷裂纹流变断裂分析程序，得到不同卸荷条件下，随机裂纹瞬态起裂和流变扩展终止情况的原生裂纹和卸荷裂纹分布图。图8所示为最小主应力卸荷至0.1σ₁(2 MPa)和0 MPa时，裂纹瞬态起裂和流变扩展终止情况下原生裂纹和卸荷裂纹分布图。

对比卸荷裂纹的瞬态起裂和流变断裂终止2种不同状态下的裂纹网络，发现最小主应力卸荷至0.1σ₃时，流变断裂终止状态的裂纹密度增长不大，卸荷裂纹流变扩展效应不强。而最小主应力卸荷至0 MPa时，裂纹流变断裂效应显著，卸荷裂纹流变断裂导致岩体裂纹密度、展布都发生明显变化。图9所示为不同卸荷状态下卸荷裂纹瞬态起裂总长度和流变扩展总长度的变化曲线。由图9可以看出：随最小主应力卸荷量的增加，卸荷裂纹的瞬态起裂长度和流变扩展长度呈非线性增长。当最小主应力在0.1σ₃~σ₃之间，卸荷裂纹基本上没有显现。最小主应力卸荷至0 MPa时，卸荷裂纹的瞬态起裂长度和流变扩展长度分别是卸荷至0.3σ₃时的13.90和7.38倍；是卸荷至0.1σ₃时的1.93和2.19倍。可见当最小主应力接近0 MPa时，对最小主应力较小的扰动变化，将导致卸荷裂纹的成倍增加。

表1  断续裂纹组几何参数

Table 1  Geometric parameters of discontinuous crack sets

图8  不同卸荷状态下原生裂纹和卸荷裂纹分布

Fig. 8  Distribution of primary crack and unloading crack under different unloading states

表2  断续裂纹组几何参数

Table 2  Geometric parameters of discontinuous crack sets

根据岩体裂纹流变扩展理论，岩体裂纹流变扩展经历一定时间后会停止扩展，即止裂。对裂纹岩体每个裂纹逐一进行流变扩展时间分析，得到每条裂纹的扩展流变的寿命。以460号，448号和209号裂纹为例，来研究岩体裂纹流变扩展。图10所示为460号，448号和209号裂纹的分布。以最小主应力卸荷至0.1σ₃和0 MPa为例，研究卸荷岩体裂纹的流变断裂效应。

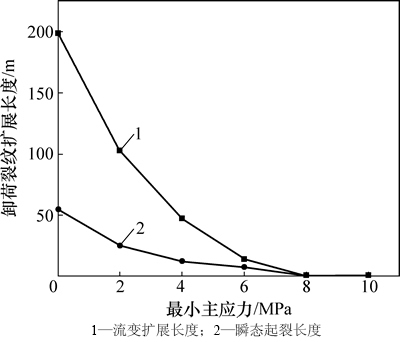
图9  不同卸荷状态卸荷裂纹扩展

Fig. 9  Unloading crack extension under variable unloading states

图10  460号，448号和209号裂纹的分布

Fig. 10  Distribution of cracks No. 460, No. 448 and No. 209

图11所示为最小主应力卸荷至0.1σ₃时，460号和448号裂纹的流变扩展长度曲线，其曲线突出地显示了裂纹流变断裂的衰减流变阶段和定常流变阶段。计算得到460号裂纹流变扩展时间为16.74 h，裂纹扩展长度0.094 m；448号裂纹流变扩展时间为18.75 h，裂纹扩展长度0.087 m，2条裂纹没有和其他裂纹贯通。209号裂纹在最小主应力卸荷至0.1σ₃下，没有起裂扩展。

图12所示为最小主应力卸载至0 MPa时，460号和448号裂纹的流变断裂扩展曲线。比较图11和图12发现：随着最小主应力的卸载，裂纹流变扩展长度增加。最小主应力卸载至0 MPa时，460号和448号裂纹流变扩展长度分别为1.127 m和0.932 m，其流变扩展时间分别为1 595.14 h和1 318.95 h。卸载至0 MPa时流变扩展长度远大于卸载至0.1σ₃时流变扩展长度，从而导致前者流变扩展时间远大于后者流变扩展时间。

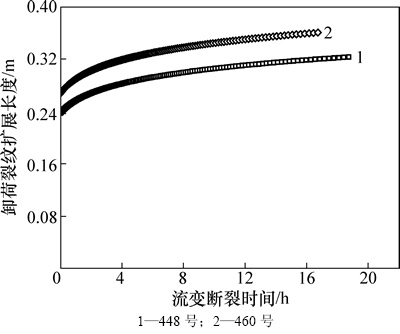
图11  最小主应力卸荷至0.1σ₃时460号和448号裂纹的流变断裂曲线

Fig. 11  Rheological fracture curves of cracks No. 460 and No. 448 during minimum principle stress down to 0.1σ₃

需要说明的是460号裂纹在流变扩展1.127 m后与其他裂纹贯通而止裂。448号裂纹的止裂判剧采用裂纹尖端的K_I＜K₀。两者止裂的计算判剧不同。

对于209号裂纹，存在裂纹扩展前的孕育期，即延迟起裂。最小主应力卸荷至0 MPa时，209号裂纹的流变断裂曲线如图13所示。计算得裂纹起裂孕育时间为38.72 h，裂纹经历孕育(延迟起裂)后，裂纹进入流变断裂阶段。209号裂纹最终扩展长度为0.64 m。

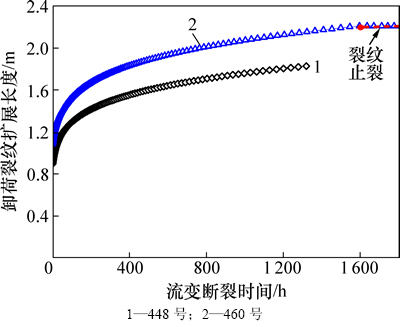
图12  最小主应力卸荷至0 MPa时460号和448号裂纹的流变断裂曲线

Fig. 12  Rheological fracture curves of cracks No. 460 and No. 448 during minimum principle stress down to 0 MPa

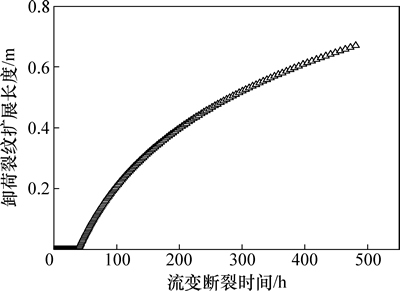
图13  最小主应力卸荷至0 MPa时209号裂纹的流变断裂曲线

Fig. 13  Rheological fracture curve of crack No. 209 during minimum principle stress down to 0 MPa

4  结论

1) 随机卸荷裂纹的流变断裂分析模型从岩石断裂力学和流变力学角度出发合理地解释了卸荷裂纹发生的随机性和发生时间的滞后性。

2) 卸荷岩体裂纹的流变断裂与岩石流变过程相似，呈现出衰减流变阶段、定常流变阶段2个阶段。

3) 随着最小主应力σ₃的卸荷，岩体裂纹瞬态扩展和流变扩展都增强，最小主应力接近0 MPa时，对最小主应力较小的扰动变化，将导致卸荷裂纹的成倍增加。

4) 随机卸荷裂纹流变断裂模型的建立为进一步开展卸荷岩体变形损伤特性的研究提供了细观层面上的理论依据。

参考文献：

[1] 吴刚, 孙钧. 卸荷应力状态下裂纹岩体的变形和强度特性[J]. 岩石力学与工程学报, 1998, 17(6): 615-621.

WU Gang, SUN Jun. Deformation and strength character soft jointed rock mass under unloading stress states[J]. Chinese Journal of Rock Mechanic sand Rock Engineering, 1998, 17(6): 615-621.

[2] 周维垣, 杨若琼, 剡公瑞. 岩体边坡非连续非线性卸荷及流变分析[J]. 岩石力学与工程学报, 1997, 16(3): 210-216.

ZHOU Weiyuan, YANG Ruoqiong, YAN Gongrui. Nonlinear and discontinuous deformation and rheological analysis for unloaded rock slopes[J]. Chinese Journal of Rock Mechanics and Engineering, 1997, 16(3): 210-216.

[3] Martino J B, Chandler N A. Excavation-induced damage studies at the underground research laboratory[J]. International Journal of Rock Mechanics and Mining Sciences, 2004, 41(8): 1413-1426.

[4] 哈秋舲. 岩石边坡工程与卸载非线性岩石(体)力学[J]. 岩石力学与工程学报, 1997, 16(4): 86-391.

HA Qiuling. Rock slope engineering and unload in nonlinear rock mass mechanics[J]. Chinese Journal of Rock Mechanics and Engineering, 1997, 16(4): 386-391.

[5] 陈德基, 余永志, 马能武, 等. 三峡工程永久船闸高边坡稳定性研究中的几个主要问题[J]. 工程地质学报, 2000, 8(1): 7-15.

CHEN Deji, YU Yongzhi, MA Nengwu, et al. Some main problems on the stability of high permanent shiplock slope for Three Gorges Project[J]. Journal of Engineering Geology, 2000, 8(1): 7-15.

[6] 李建林, 王乐华. 卸荷岩体的尺寸效应研究[J]. 岩石力学与工程学报, 2003, 22(12): 2032-2036.

LI Jianlin, WANG Lehua. Study on size effect of unloaded rock mass[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(12): 2032-2036.

[7] 郑文翔, 赵延林, 王敏. 单轴压缩条件下预制裂隙类岩石材料实验研究[J]. 湖南科技大学学报(自然科学版), 2014, 28(4): 1-6.

ZHENG Wenxiang, ZHAO Yanlin, WANG Min. Experimental study on rock like material with crack under uniaxial compression[J]. Journal of Hunan University of Science & Technology (Natural Science Edition), 2014, 28(4): 1-6.

[8] Maejima T, Morioka H, Mori T, et al. Evaluation of loosened zones on excavation of a large underground rock cavern and application of observational construction techniques[J]. Tunnelling and Underground Space Technology, 2003, 18(2/3): 223-232.

[9] Backblom G. Recent experiments in hard rocks to study the excavation response: Implications for the performance of a nuclear waste geological repository[J]. Tunnelling and Underground Space Technology, 1999, 14(3): 377-394.

[10] 李洪生, 李树清, 汤铸, 等. 近距离煤层群叠加开采卸压效应的数值模拟分析[J]. 矿业工程研究, 2014, 29(3): 48-52.

LI Hongsheng, LI Shuqing, TANG Zhu, et al. Numerical simulation on superposition mining pressure relief effect of near distance coal seam group[J]. Mineral Engineering Research, 2014, 29(3): 48-52.

[11] 沈军辉, 王兰生, 王青海, 等. 卸荷岩体的变形破裂特征[J]. 岩石力学与工程学报, 2003, 2(12): 2028-2031.

SHEN Junhui, WANG Lansheng, WANG Qinghai, et al. Deformation and fracture features of unloaded rock mass[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(12): 2028-2031.

[12] 周小平, 哈秋聆, 张永兴, 等. 峰前围压卸荷条件下岩石的应力-应变全过程分析和变形局部化研究[J]. 岩石力学与工程学报, 2005, 24(18): 3236-3245.

ZHOU Xiaoping, HA Qiuling, ZHANG Yongxing, et al. Analysis of localization of deformation and complete stress-strain relation for mesoscopic heterogeneous brittle rock materials when axial stress is held constant while lateral confinement is reduced[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(18): 3236-3245.

[13] 李建林. 卸荷岩体力学[M]. 北京: 中国水利水电出版社, 2003: 12-50.

LI Jianlin. Unloading rock mass mechanics[M]. Beijing: China Water Power Press, 2003: 12-50.

[14] 袁和勇, 葛新玉, 胡嘉伟, 等. 动压巷道在不同采动下的支护效果模拟分析[J]. 矿业工程研究, 2014, 29(3): 13-18.

YUAN Heyong, GE Xinyu, HU Jiawei, et al. Dynamic pressure in different mining situations supporting effect simulation analysis[J]. Mineral Engineering Research, 2014, 29(3): 13-18.

[15] 李廷春, 张仕林, 王群, 等. 立井破碎基岩段围岩强度及支护等级划分标准[J]. 湖南科技大学学报(自然科学版), 2014, 29(1): 1-7.

LI Tingchun, ZHANG Shilin, WANG Qun, et al. Classification standard of strength and supporting level for surrounding rock in shaft broken bedrock section[J]. Journal of Hunan University of Science & Technology (Natural Science Edition), 2014, 29(1): 1-7.

[16] 陶振宇, 潘别桐. 岩石力学原理与方法[M]. 北京: 中国地质大学出版社, 1991: 23-30.

TAO Zhenyu, PAN Bietong. Principle and method of rock mechanics [M]. Beijing: China University of Geosciences Press,1991: 23-30.

[17] Horri H, Nemat-Nasswer S. Brittle failure in compression: splitting, faulting and brittle-ductile transition[J]. Philosophical Transactions of the Royal Society A: Mathematical Physical and Engineering Science, 1986, 319(A): 337-374.

[18] Sahouryeh E, Dyskin A V, Germanovich L N. Crack growth under biaxial compression[J]. Engineering Fracture Mechanics, 2002, 69(18): 2187-2198.

[19] 周筑宝. 蠕变断裂应力强度因子及应用[J]. 固体力学学报, 1983, 5(1): 101-104.

Zhou zhubao. Creep fracture stress intensity factor and application[J]. Acta Mechanica Solida Sinica, 1983, 5(1): 101-104.

[20] 赵延林, 万文, 王卫军, 等. 类岩石裂纹压剪流变断裂与亚临界扩展实验及破坏机制[J]. 岩土工程学报, 2012, 34(6): 1050-1059.

ZHAO Yanlin, WAN Wen, WANG Weijun, et al. Compressive-shear rheological fracture of rock-like cracks and subcritical crack propagation test and fracture mechanism[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(6): 1050-1059.

[21] 易顺民. 裂纹岩体损伤力学导论[M]. 北京: 科学出版社, 2005: 40-45.

YI Shunmin. Introduction to damage mechanics fractured rock[M]. Beijing: Science Press, 2005: 40-45.

[22] Ashby M F, Hallam S D. The failure of brittle solids containing small cracks under compressive stress states[J]. Acta Metall, 1986, 34(3): 497-510.

[23] 李江腾, 曹平, 袁海平. 岩石亚临界裂纹扩展试验及门槛值研究[J]. 岩土工程学报, 2006, 28(3): 415-418.

LI Jiangteng, CAO Ping, YUAN Haiping. Study on subcritical crack growth and thresholds of rocks[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(3): 415-418.

[24] 赵延林, 曹平, 文有道, 等. 岩石黏弹塑性流变实验和非线性流变模型研究[J]. 岩石力学与工程学报, 2008, 27(3): 477-487.

ZHAO Yanlin, CAO Ping, WEN Youdao, et al. elastovisco- plastic rheological experiment and nonlinear rheological model of rocks[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(3): 477-487.

(编辑  赵俊)

收稿日期：2015-01-09；修回日期：2015-03-16

基金项目(Foundation item)：国家自然科学基金资助项目(51274097，51434006，51174088)；湖南省自然科学基金资助项目(2015JJ2067)；湖南省教育厅资助科研项目(13A020)；中国矿业大学煤炭资源与安全开采国家重点实验室开放基金资助项目(13KF03)(Projects (51274097，51434006, 51174088) supported by the National Natural Science Foundation of China；Project (2015JJ2067) supported by the Natural Science Foundation of Hunan Province; Project (13A020) supported by the Scientific Research Fund of Hunan Provincial Education Department of China; Project (13A020) supported by the Open Projects of State Key Laboratory of Coal Resources and Safe Mining, CUMT)

通信作者：赵延林，博士，副教授，从事岩石流变断裂力学研究；E-mail：yanlin_8@163.com