J. Cent. South Univ. Technol. (2010) 17: 349-356

DOI: 10.1007/s11771-010-0052-0                                                                                                                  

A novel particle swarm optimizer without velocity: Simplex-PSO

XIAO Hong-feng(肖宏峰), TAN Guan-zheng(谭冠政)

School of Information Science and Engineering, Central South University, Changsha 410083, China

? Central South University Press and Springer-Verlag Berlin Heidelberg 2010

                                                                                                

Abstract: A simplex particle swarm optimization (simplex-PSO) derived from the Nelder-Mead simplex method was proposed to optimize the high dimensionality functions. In simplex-PSO, the velocity term was abandoned and its reference objectives were the best particle and the centroid of all particles except the best particle. The convergence theorems of linear time-varying discrete system proved that simplex-PSO is of consistent asymptotic convergence. In order to reduce the probability of trapping into a local optimal value, an extremum mutation was introduced into simplex-PSO and simplex-PSO-t (simplex-PSO with turbulence) was devised. Several experiments were carried out to verify the validity of simplex-PSO and simplex-PSO-t, and the experimental results confirmed the conclusions: (1) simplex-PSO-t can optimize high-dimension functions with 200-dimensionality; (2) compared PSO with chaos PSO (CPSO), the best optimum index increases by a factor of 1×10²-1×10⁴.

Key words: Nelder-Mead simplex method; particle swarm optimizer; high-dimension function optimization; convergence analysis

                                                                                                           

1 Introduction

Since Kennedy proposed particle swarm optimizer (PSO) in 1995, many scholars have been improving  PSO. Their methods may be divided into four categories: (1) adjust and control velocity [1-4]; (2) keep diversity of particles to reduce the chances of trapping into a local optimum [5-7]; (3) devise hybrid PSO [8-11]; and (4) devise parallel PSO [12-14]. Though so many improved approaches were used, it is still difficult for PSO to optimize high dimensionality functions, because the particles would stagnate when PSO is in the later stage of evolutionary process, thus leading to performance decrease in precision and speed.

Some scholars ever proposed several PSO, in which the velocity term of PSO was deleted. In 2003, KENNEDY and EBERHART [15] first proposed a PSO without velocity term, called bone bare PSO. In 2006, CHRISTOPHER and KEVIN [16] presented a PSO without the velocity term. In 2007, HU and LI [17] presented a simpler PSO, where the velocity term was discarded, too.

The Nelder-Mead simplex method (NMSM) [18] was proposed in 1965 and has been used widely in engineering optimization fields. Some scholars fused it into evolution algorithms (EAs) and devised some hybrid evolution algorithms based on simplex [19-20]. If a vertex of NMSM is looked as a particle of PSO, the centroid of vertexes in a simplex accordingly becomes the centroid of particles in PSO. From information processing, the centroid of particles reflects synthetic information of particles and should be a reference objective of PSO. From recognition and learning, the best particle is a competitor, who is similar to a leader; while the centroid embodies the intelligence of the masses. According to the materialistic view of history, both leader and the masses advance the whole society and are our learning models. Based on the two sides, it is reasonable that the simplex-PSO is an algorithm based on the mechanism of learning, competition and cooperation.

The simplex-PSO is a novel swarm intelligent computation. (1) A cooperation idea is first introduced into the PSO and thus the simplex-PSO is based on learning, competition and cooperation. (2) The simplex- PSO is a fusion of two kernel ideas of NMSM and PSO and is completely different from simplex-HPSO (hybrid PSO based on simplex), which is combination of PSO and NMSM, because the NMSM only acts as a complementary operator of PSO.

The simplex-PSO has the capacity of fast optimizing high-dimensionality functions and high computation precision, which provides us a new approach to optimize membership functions in fuzzy systems, neural network and complex control system because these optimization problems are always high- dimensionality functions.

2 Nelder-Mead simplex method

The kernel ideas of the Nelder-Mead simplex method include two-fold: one is an estimation of gradient, which is the direction vector g from the worst vertex X_w through the centroid 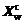 of all vertexes except the worst vertex X_w; the other is substituting iteratively a new vertex better than the worst vertex X_w for the worst vertex to compose a new simplex. A new vertex is produced by one of the four operators: reflection, expansion, outer contraction and inner contraction. 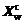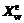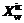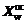As shown in Fig.1, , ,  and  are the vertexes of reflection, expansion, inner contraction and outer contraction operations, respectively.

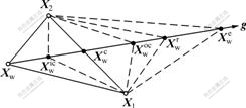
Fig.1 Four operations in Nelder-Mead simplex method

The four operations of NMSM are written as

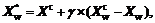 -1≤γ≤2           (1)

where 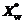 represents a reflection vertex, expansion vertex, inner contraction vertex, or outer contraction vertex of the worst vertex; γ denotes reflection coefficient, expansion coefficient, inner contraction coefficient or outside contraction coefficient respectively when it is in different intervals; and 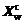is the centroid of all vertexes except the worst vertex X_w, i.e.,

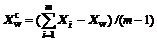                    (2)

where m denotes the number of simplex vertexes; and X_i is a vertex of a simplex with m vertexes.

3 Simplex-PSO

3.1 Derivation of simplex-PSO

Notice further that

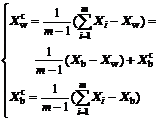                   (3)

where X_b and 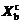 denote the best vertex and the centroid of all vertexes except the best vertex, respectively. Hence, substituting Eq.(3) into Eq.(1) yields the equation

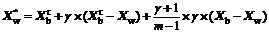   (4)

Since γ+1≤3, let γ=3α-1, 0≤α≤1. Eq.(4) becomes

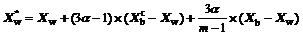
   (5)

Eq.(5) is derived from the worst vertex; if the form of Eq.(5) is popularized to other simplex vertexes and factor γ₀ is introduced into the first term X_w, a common form will be given by

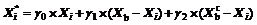     (6)

where γ₁=3α/(m-1), γ₂=3α-1. Vertex X_i is looked as the ith particle of the kth generation, i.e., X_i(k), and X_i is looked as the ith particle of the (k+1)th generation reasonably, i.e., X_i(k+1). The discrete equation corresponding to Eq.(6) is written as

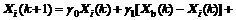
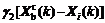                  (7)

Assume that γ₀=c₀, γ₁=c₁×rand₁( )=c₁γ₁, and γ₂=  c₂×rand₂( )=c₂γ₂, where c₀, c₁, and c₂ are constants, and rand₁( ) and rand₂( ) are functions, which generate two random numbers γ₁ and γ₂ in the interval (0, 1). Hence, the equivalent form of Eq.(7) is

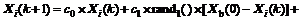
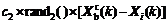         (8)

Eq.(8) is derived from the Nelder-Mead simplex method and similar to PSO, so we call it simplex-PSO.

According to Eq.(8), the reference objectives of simplex-PSO are the best particle and the centroid of the particles except the best particle. From information processing, the centroid reflects synthetic information of all particles and is influenced by changes of all particles’ position. Therefore, the centroid reference objective is updated promptly and effectively.

3.2 State-space equation of simplex-PSO

Let X(k)=[X_i(k), …, X_m(k)]^T, and Eq.(8) is written as a state-space matrix equation

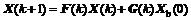               (9)

Eq.(9) is a linear discrete time-varying system, where both F(k) and G(k) are m×m matrixes:

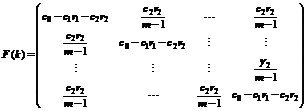
4 Convergence of simplex-PSO

4.1 Theorems of stability and convergence

Lemma 1 [21]: Asymptotic stability. Given a linear discrete time-varying system

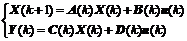
which remains asymptotic stability, only if

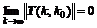
where T is transfer matrix and is defined as

 

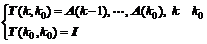
Lemma 2 [21]: Consistent asymptotic convergence. Given a linear discrete time-varying system

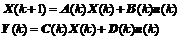
which remains consistent asymptotic convergence, if and only if

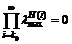
where 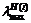 is the maximum of all eigenvalues of matrix H(k), H(k)=A^T(k)A(k).

Lemma 3 [21]: Gerschgorin theorem. Each eigen- value of matrix B lies in at least one of the discs with

centers b_ii and radius .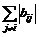

4.2 Convergence condition of simplex-PSO

Theorem: The simplex-PSO remains consistent asymptotic stability and asymptotic convergence, if

 

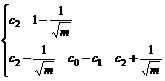
Proof: (1) Analyze asymptotic stability.

Matrix F(k) is symmetry and its Frobenius norm is

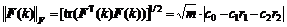
(10)

Note further that the Frobenius norm is a consistent norm. According to the definition of transfer matrix T(k, k₀) in lemma 1, transfer matrix T(k, k₀) of system (9) is given by

≤

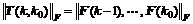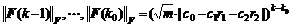
(11)

Since |c₀-(c₁+c₂)|≤|c₀-(c₁r₁+c₂r₂)|, assume that

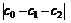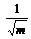≤                         (12)

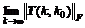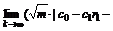
such that 0≤≤  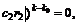and 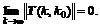According to lemma 1, the simplex PSO of is of asymptotic stability.

(2) Analyze consistent asymptotic convergence by the following steps (i)-(iii).

(i) Evaluate eigenvalues of matrix F(k). According to Gerschgorin theorem (e.g., Lemma 3), each eigenvalue λ^F of matrix F(k) lies in the Gerschgorin disc

|c₀-c₁r₁-c₂r₂|≤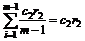                 (13)

Matrix F(k) is symmetry and its eigenvalues are real. The maximum eigenvalue and minimum eigenvalue of matrix F(k) are

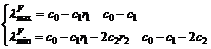             (14)

 (ii) Evaluate eigenvalues of matrix H(k).

According to lemma 2, matrix H(k) corresponding to Eq.(9) is defined as H(k)=F ^T(k)F(k)= F²(k). If an eigenvalue of matrix F(k) is λ^F, an eigenvalue of matrix H(k) will be (λ^F)², i.e., λ^H(k)=(λ^F(k))².

(iii) Evaluate the maximum eigenvalue of matrix H(k).

Consider case 1:

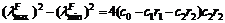≥0

the maximum eigenvalue of matrix H(k) is (c₀-c₁r₁)². According to lemma 2, assume that

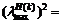(c₀-c₁r₁)＜(c₀-c₁)²＜1               (15)

where ≤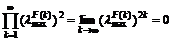. In addition, all elements of matrix F(k) should be positive numbers. If c₀-c₁-c₂＞0, then the elements of matrix F(k) will be positive, i.e.,

c₀-c₁r₁-c₂r₂＞c₀-c₁-c₂＞0                     (16)

Combining expressions (12), (15) and (16) yields the inequality

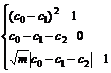                             (17)

The solution to inequality (17) is set

c₂≤c₀-c₁≤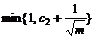                  (18)

Consider case 2

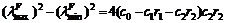＜0

In view of the process of case 1, in turn we get

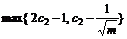≤c₀-c₁≤c₂             (19)

Expressions (18) and (19) are synthesized as

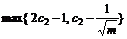≤c₀-c₁≤ 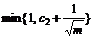(20)

When expression (20) is satisfied, the simplex PSO is of asymptotic convergence. Further assume that

c₂≤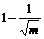                                (21)

This gives a simpler expression

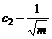≤c₀-c₁≤ 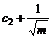                 (22)

When conditions (21)-(22) are satisfied, simplex- PSO is of consistent asymptotic convergence and stability.

4.3 Numerical experiments for simplex-PSO

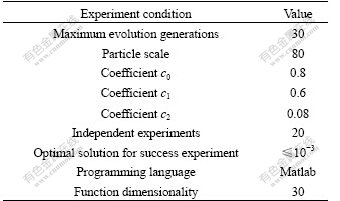
4.3.1 Experiment conditions

Experiment 1 is used to verify the validity of simplex-PSO, and the experimental conditions are listed in Table 1.

Table 1 Conditions of experiment 1

4.3.2 Benchmark functions

Benchmark functions are as follows.

(1) Ackley:

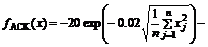
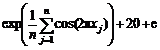
(2) Griewank:

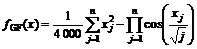
(3) Lenvy Monta 1(LM1):

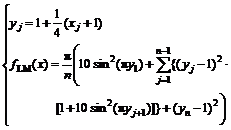
(4) Rastrigin:

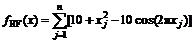
(5) Rosenbrock:

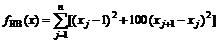
(6) Sphere:

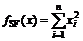
4.3.3 Results of experiment 1

Table 2 lists the results of 20 independent experiments and confirms that simplex-PSO is correct.

Table 2 Comparison results of experiment for optimizing 30 dimensionalities benchmark functions using simplex-PSO

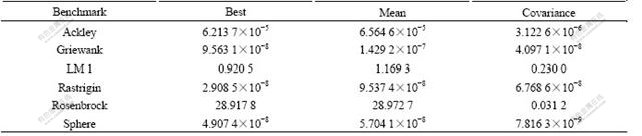
In Table 2 and Tables 4-6, best optimum, worst optimum, mean and covariance denote the best optimal solution, the worst optimal solution, the average value of all optimal solutions and the covariance of all optimal solutions respectively in 20 independent experiments; a successful experiment denotes the optimal solution of an experiment is less than or equal to 1×10^-3; success ratio  (SR) is defined as the number of successful experiments divided by the number of all independent experiments.

5 Simplex-PSO-t

5.1 Improving strategy

An improved approach is used for the simplex-PSO because the simplex-PSO easily traps into a local extremum. In PSO, particles “find” a good solution during moving process. When particles stop moving, simplex-PSO will have no chance to find a better solution and all particles surround the best particle. When the best particle breaks the blockade it will prompt the other particles to move again. A simple and effective approach of breaking the blockade is random turbulence in a neighbor; namely, extremum mutation is used for the best particle in this paper and the best particle is accepted by a certain probability. The simplex-PSO with turbulence is called simplex-PSO-t, which is

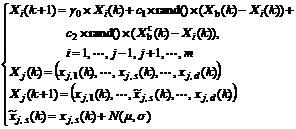
(23)

where X_j(k) is the best particle of the kth generation; s is the turbulence position, i.e., the sth component; d is the dimensionality of objective function; and 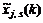is the sth component after turbulence.

5.2 Experiments for simplex-PSO-t

5.2.1 Testing functions and comparison algorithms

The testing functions are the same as those of experiment 1. The comparison algorithms are as follows:

(1) NM-SA, Nelder-Mead simplex method simulation anneal [22].

(2) AWPSO, adaptive weight particle swarm optimizer [23].

(3) MIEA, multi-population information- guid EA [24].

(4) G3-PCX, parent centric crossover [25].

(5) G3HM, G3-PCX with hybrid mutation [26].

(6) RCGAQS, real-coded genetic algorithm with aquasic-simplex [27].

(7) RGA-ASBX, real-coded genetic algorithm with adaptive simulated binary crossover [28].

(8) CPSO [8].

5.2.2 Numerical experiment classification

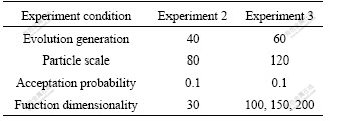
Experiment 2 is a comparison experiment between simplex-PSO-t and the first seven EAs in section 5.1 and experiment 3 between simplex-PSO-t and CPSO in section 5.1. The conditions of experiments 2-3 are listed in Tables 1 and 3.

Table 3 Conditions of experiments 2-3

5.2.3 Results of experiments

(1) Table 4 lists the comparison results of experiment 2, which shows that the precision of simplex- PSO-t is superior to that of the above seven EAs (1)-(7) and simplex-PSO, and confirms that the turbulence is beneficial to escaping a local extremum.

(2) Tables 5-6 list the comparison results of optimizing high-dimension functions (e.g., experiment 3). The evolutionary charts are sketched in Fig.2, where label Y is the logarithm of absolute value of function value, i.e., lg f_a. Tables 5-6 and Fig.2 show that simplex- PSO-t is able to optimize high-dimension functions.

Table 4 Comparison results of experiment 2 for optimizing 30-dimensionalily benchmark functions using simplex-PSO-t

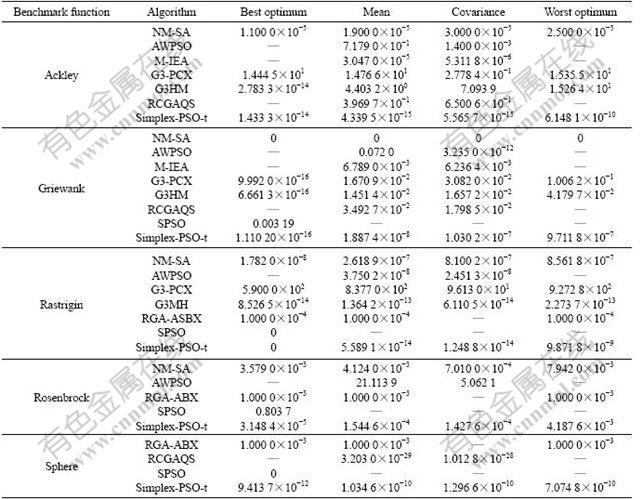
Table 5 Comparison results of experiment 3 for optimizing 100-200 dimensionalities functions using simplex-PSO-t

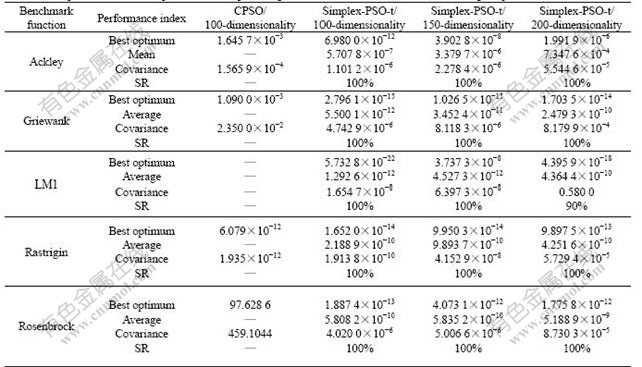
Table 6 Comparison results of experiment 3 for optimizing 100-200 dimensionalities functions using simplex-PSO-t

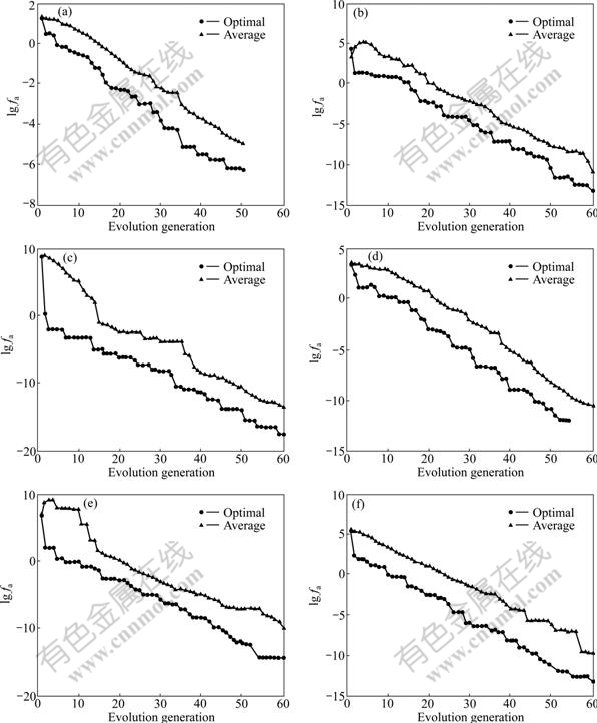
Fig.2 Evolution charts of the fifth experiment of above six benchmark functions in experiment 3: (a) 200-dimensionality Ackley function; (b) 200-dimensionality Griewank function; (c) 200-dimensionality LM1 function; (d) 200-dimensionality Rastrigin function; (e) 200-dimensionality Rosenbrok function; (f) 200-dimensionality Sphere function

6 Conclusions

(1) The simplex-PSO is a new PSO based on learning, competition, and cooperation mechanism, and the centroid embodies the cooperation method.

(2) The simplex-PSO is convergent. The convergence theorem shows that velocity term in PSO may be discarded during the evolutionary process.

(3) The simplex-PSO-t is simpler and more effective than PSO for abandoning of velocity term and has the capacity of optimizing high-dimension functions.

References

[1] CLERC M. Stagnation analysis in particle swarm optimizer [R]. Colchester: Department of Computer Science, University of Essex, 2006.

[2] CLERC M, KENNEDY M. The particle swarm-explosion, stability, and convergence in multidimensional complex space [J]. IEEE Transaction on Evolutionary Computation, 2002, 6(1): 58-73.

[3] LANGDON W B. Kernel methods for PSOs [R]. Colchester: Department of Computer Science, University of Essex, 2005.

[4] ROBERTO B, MAURO B, SRINIVAS P. Do not be afraid of local minima [R]. Trento: Department of Information and Communication Technology, University of Trento, 2005.

[5] AUGER A, HANSEN N. A restart CMA evolution strategy with increasing population size [C]// CORNE D, MICHALEWICZ Z, MCKAY B, FOGEL D. Proceeding of the 2005 IEEE Congress on Evolutionary Computation. Edinburgh: IEEE Press, 2005: 1769-1775.

[6] E Gang-qiang, XUN Shi-yu. Particle swarm optimization based on dynamic population size [J]. Information and Control, 2008, 37(1): 18-27. (in Chinese)

[7] LI Ting, LAI Xu-zhi, WU Min. A novel two-swarm based particle swarm optimization algorithm for optimal power flow problem [J]. Journal of Central South University: Science and Technology, 2007, 38(1): 133-137. (in Chinese)

[8] LIU Hong-bo, WANG Xiu-kun, TAN Guo-zhen. Convergence analysis of particle swarm optimization and improvement of chaotic [J]. Control and Decision, 2006, 21(6): 636-640. (in Chinese)

[9] LANGDON W B, RICCARDO P. Evolving problems to learn about particle swarm and other optimizers [C]// EDINBURGH. Proceedings of the 2005 Genetic and Evolutionary Computation Conference for ACM SIGEVO (GECCO2005). New York: ACM Press, 2005: 81- 88.

[10] LIU Bo, WANG Ling, JIN Yi-hui, TANG Fang, HUANG De-xian. Improved particles swarm optimization combined with chaos [J]. Chaos, Solitons and Fractals, 2005, 25(5): 1261-1271.

[11] LEE H P, LIANG Y C. An improved GA and a novel PSO-GA-based hybrid algorithm [J]. Information Processing Letters, 2005, 93(5): 255-261.

[12] GUANG Qiang-li, ZHAO Feng-qiang. Parallel hybrid PSO-GA algorithm and its application to layout design [J]. Structural and Multidisciplinary Optimization, 2006, 33(5): 749-758.

[13] GEORGE A D, HAFTKA R T. Parallel asynchronous particle swarm optimization [J]. International Journal for Numerical Method in Engineering, 2006, 67(5): 578-595.

[14] SCHUFFE J F, REINBOLT J A. Parallel global optimization with particle swarm algorithm [J]. International Journal of Numerical Methods in Engineering, 2004, 61(13): 2296-2315.

[15] KENNEDY J, EBERHART R C. Bare bones particle swarms [J]. Evolution Computation, 2003, 12(6): 258-265.

[16] CHRISTOPHER K, KEVIN D. The Kalman swarm: A new approach to particle motion in swarm optimization [C]// SAHNI S. Proceedings of the third IASTED International Conference Advances in Computer Science and Technology. Calgary: ACTA Press, 2007: 606-614.

[17] HU Wang, LI Zhi-shu. A simpler and more effective particle swarm optimization [J]. Journal of Software, 2007, 18(4): 861-868. (in Chinese)

[18] NELDER J A, MEAD R. A simplex method for function minimum [J]. Computer Journal, 1965, 7(2): 308-313.

[19] HELIO J C, CARLILE C L. A GA-simplex hybrid algorithm for global minimization of molecular potential energy functions [J]. Annals of Operation Research, 2005, 38(1): 189-202.

[20] WANG Fang, QIU Yu-hui. A novel particle swarm algorithm using simplex method [J]. Information and Control, 2005, 34(1): 9-14. (in Chinese)

[21] XIAO Yang. Analysis of dynamical systems [M]. Beijing City: Beifang Jiaotong University Press, 2002: 64-73. (in Chinese)

[22] YEN J, LIAO J C, BOGJU G. A hybrid approach to modeling metabolic systems using a genetic algorithm and simplex method [J]. Parallel Computing, 2002, 28(2): 173-191.

[23] MAHFOUF M, LINKENS D A. Adaptive weighted swarm optimization for multiobjective optimal design of alloy steels [R]. Colchester: Department of Computer Science, University of Essex, 2006.

[24] CHEN Wei, SHI Shang-jang. The development of information guided evolution algorithm for global optimization [J]. Journal of Global Optimization, 2006, 36(4): 517-535.

[25] JASON T, NOR R M. Hybridizing adaptive and non-adaptive mutation for cooperative exploration of complex multimodal search space [C]// SAHNI S. Proceedings of the third IASTED International Conference Advances in Computer Science and Technology. Calgary: ACTA Press, 2007: 476-498.

[26] ZHANG Guo-li, LU Hai-yan. Hybrid real-coded genetic algorithm with quasic-simplex technology [J]. International Journal of Computer Science and Network Security, 2006, 6(10): 246-256.

[27] DEB K, ANAND A, JOSHI D. A computationally efficient evolutionary algorithm for real-parameter evolution [J]. Evolutionary Computation, 2005, 13(4): 371-395.

[28] DEB K, SINDHYA K, OKABE T. Self-adaptive simulated binary crossover for real-parameter optimization [C]// Proceedings of the 2007 Genetic and Evolutionary Computation Conference for ACM SIGEVO (GECCO-2007). New York: ACM Press, 2007: 414-419.

                     

Foundation item: Project(50275150) supported by the National Natural Science Foundation of China; Project(20070533131) supported by Research Fund for the Doctoral Program of Higher Education of China

Received date: 2009-04-16; Accepted date: 2009-08-04

Corresponding author: TAN Guan-zheng, PhD, Professor; Tel: +86-731-88716259; E-mail: tgz@yahoo.com.cn

(Edited by LIU Hua-sen)