J. Cent. South Univ. (2018) 25: 241-250

DOI: https://doi.org/10.1007/s11771-018-3733-8

Theoretical analysis of adaptive harmonic window and its application in frequency extraction of vibration signal

LI Shun-ming(李舜酩)¹, WANG Jin-rui(王金瑞)¹, LI Xiang-lian(李香莲)²

1. College of Energy and Power Engineering, Nanjing University of Aeronautics and Astronautics,Nanjing 210016, China;

2. College of Science, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2018

Abstract: The goal of this paper is to find an excellent adaptive window function for extracting the weak vibration signal and high frequency vibration signal under strong noise. The relationship between windowing transform and filtering is analyzed first in the paper. The advantage of adjustable time-frequency window of wavelet transform is introduced. Secondly the relationship between harmonic wavelet and multiple analytic band-pass filter is analyzed. The coherence of the multiple analytic band-pass filter and harmonic wavelet base function is discussed, and the characteristic that multiple analytic band-pass filter included in the harmonic wavelet transform is founded. Thirdly, by extending the harmonic wavelet transform, the concept of the adaptive harmonic window and its theoretical equation without decomposition are put forward in this paper. Then comparing with the Hanning window, the good performance of restraining side-lobe leakage possessed by adaptive harmonic window is shown, and the adaptive characteristics of window width changing and analytical center moving of the adaptive harmonic window are presented. Finally, the proposed adaptive harmonic window is applied to weak signal extraction and high frequency orbit extraction of high speed rotor under strong noise, and the satisfactory results are achieved. The application results show that the adaptive harmonic window function can be successfully applied to the actual engineering signal processing.

Key words: window function; Fourier transform; filter; harmonic wavelet; adaptive; vibration signal extraction

Cite this article as: LI Shun-ming, WANG Jin-rui, LI Xiang-lian. Theoretical analysis of adaptive harmonic window and its application in frequency extraction of vibration signal [J]. Journal of Central South University, 2018, 25(1): 241–250. DOI: https://doi.org/10.1007/s11771-018-3733-8.

1 Introduction

It has been prevalently recognized that the analysis of vibration signal of mechanical structure by windowing transform method is very useful. Owing to that the selection of window function can affect the veracity of analysis results, so in signal processing, it is common to choose suitable window function according to the signal characteristics and research purposes [1]. There are a number of functions that can be used to analyze mechanical vibration signal [2].

In early 1978, NUTTALL [3] analyzed some window functions with very good side-lobe behavior. There are new window functions constantly proposed with the purposes of meeting the need of application. HA and PEARCE [4] modified Bartlett-Hanning Window, ZHOU and LIU [5] proposed the I₁-csch window function and applied it to the filter design, ZHANG et al [6] and WEN et al [7] improved the existing window function and proposed a different convolution window function. The subsequent development of the research mainly concentrated in the last ten years. STUATR and ANDREAS [8] designed a hypersphere window function and compared with other window functions, and applied it to digital beam forming technology and image processing. Some new window functions were proposed for applying to more special aspects. AVCI and NACAROG [9] proposed a new class of adjustable window functions based on the cosine hyperbolic function and applied it to the design of FIR filter. They then modified these adjustable window functions [10]. Many new window functions were proposed in the subsequent studies but they were mainly used in the filter design [11–13]. According to wavelet analysis, XIAO and FENG [14] proposed the combination window function in the short time Fourier transform, and applied it in different cases of time resolution ratio and frequency resolution ratio.

Usually, in dealing with complicated unstable dynamic signal, the filter characteristic of wavelet analysis in its time-frequency domain was used to show the different frequency ranges of signal in different layer [15]. A lot of theory and method concerning wavelet analysis was proposed and brought in subsequent research [16, 17]. It is of great importance to develop the filter characteristic of wavelet analysis and to form generic window function which can be easily used and generalized. The excellent characteristic of harmonic wavelet transform represents its ability in analyzing complicated signals, and it also has been well represented in relevant research [18]. Under the basis of comparison and analysis, the theoretical expression and characteristic of adaptive harmonic window based on harmonic wavelet base function and its application are presented in this work.

The paper is organized as follows: Firstly, the advantage of wavelet analysis for windowing transform and the characteristic of harmonic wavelet transform containing multiple analytic band-pass filter, unified their research and application were analyzed. Then, an excellent adaptive harmonic window based on the theory analysis and compared with Hanning window was put forward, research on adaptive harmonic window theory expression and its characteristics shows better performance of restraining leakage than Hanning window. The adaptive harmonic window is the development of wavelet analysis technique, and also the expansion and enrich of the content and application advantage of window function. Finally, the adaptive harmonic window function applied to the frequency extraction of weak signal and high frequency signal under strong noise is achieved. Compared with other methods, the adaptive harmonic window shows its advantage and can be applied to practical engineering in the signal processing.

2 Concept of windowing transform and filter

2.1 Windowing transform

In order to reflect the local characteristic of signals, a base-function that possesses good local characteristics in both time and frequency domain is expected to find. That is to say, it is fastened around a special point t₀ in time domain and point ω₀ in frequency domain. This type of base-function is window function.

The windowing Fourier transform (can be described as STFT) of signal x(t) or short time spectrum is defined as 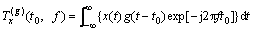[1]

     (1)

Due to multiply a short window g(t–t₀), STFT is the “local spectrum” of signal x(t) around “analyze time” t.

The same sampling interval at the time-frequency gridding point (nT, kF) is considered in the windowing Fourier transform, where T>0 and F>0 are respectively the sampling periods of time variable and frequency variable, n and k are integers. In this way, the discrete form of windowing Fourier transform and its inverse transform are given as Eqs. (2) and (3):

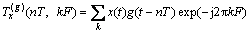     (2)

    (3)

The condition that Eqs. (2) and (3) exist is that for all the t, the Eq. (4) is satisfied.

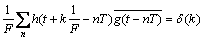            (4)

Here, δ(k) is δ function. This is the so-called “perfect reconstruction condition”.

2.2 Filter

Filter is an important technique in signal processing. Generally, the signal x(t) in mechanical system includes two parts: useful signal and interferential signal. In many cases, the frequency components of these two kinds of signals have biggish differences. So the useful signal and interferential signal can be distinguished by some methods. The interferential signal can be avoided by multiplying the frequency spectrum X(f ) of signal x(t) by a character frequency spectrum signal H(f ).

Y(f )=X(f )·H(f )                              (5)

This process is called filter [2]. And its time- domain expression is:

                      (6)

The signal’s filter form also can be digital.

2.3 Relationship between windowing transform and filter

As it is stated before, the single window function is commonly used to describe low-pass filter, the windowing Fourier transform (1) can be realized by using filter. In frequency-domain it can be expressed as the filter group [19]. It can be explained as the output of signal x(t) via a filter whose frequency response is H(f ), and multiply by 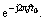Then, the planar time-frequency expression can be obtained from slipping the discretized frequency f (It can be expressed as a filter group). The band-pass realization (a) and low-pass realization (b) for windowing Fourier transform are shown in Figure 1.

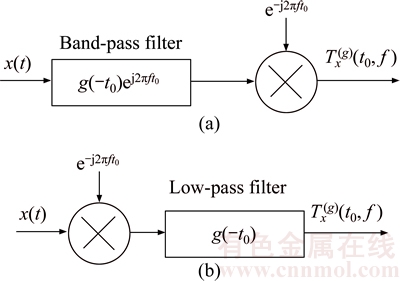
Figure 1 Band-pass realization (a) and low-pass realization (b) for windowing Fourier transform

From above analysis, it is easy to know that filter is a part of transform formula in windowing Fourier transform, and is modulated on the complex harmonic transform in a certain moment.

3 Harmonic wavelet transform and multiple analytic band-pass filter

3.1 Basic concept of harmonic wavelet transform

Commonly (and also is the need in decomposition), the dyadic wavelet and the dyadic wavelet packet transform adopt downsampling of keeping one sample out of two, that is to extract one point from two sample. In mathematic meaning, it shows the character of “binary”. NEWLAND [20] brought out a new kind of wavelet after investigating the spectrum charicteristic of Daubechise wavelet in 1993, which is called “harmonic wavelet”. The harmonic wavelet function is given by the Fourier transform of ψ_e(x) and ψ_o(x) (where the subscripts e and o respectively denote whether the real number ψ is the even function and odd function of variable x ) [21]:

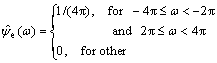          (7)

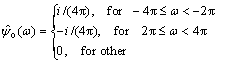         (8)

The waveform is shown in Figure 2.

Expanding the formula (7) and (8) in the inverse Fourier transform gives

    (9)

Its frequency domain waveform is shown in Figure 3. It can be seen that possesses admirable flat top shape and box characteristic. Then the complex function can be defined as harmonic wavelet.

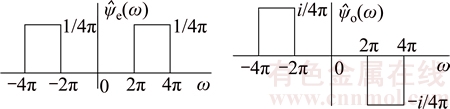
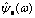Figure 2 Frequency characteristic of real even function and real odd function  [11]

Figure 3 Frequency characteristic of complex function 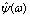 [11]

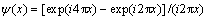           (10)

Compared with the dyadic wavelet transform, assuming that m=2^j, n=2^{j+1 in} the digital calculation, the band decomposition results in different layers are obtained based on wavelet transform

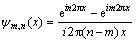                      (11)

The Eq. (11) is the common expression of harmonic wavelet in time domain. It can be seen from this formula that the harmonic wavelet does not change its phase in decomposition, and has the phase-locked function.

Assuming that the displacement length of harmonic wavelet’s analytical center is k/(n–m), then the expresion (11) changes into:

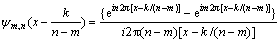(12)

That is the common expression of harmonic wavelet when the bandwidth is (n–m)2π and the analytical center is x= k/(n－m). For time-discrete signal fd(r), r=0, 1, 2, …, N–1, its harmonic wavelet transform is:

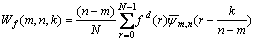    (13)

That is the discrete harmonic wavelet transform of the signal. Its expression in frequency domain is:

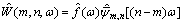              (14)

3.2 Multiple analytic band-pass filter

In 2000, “non-recursion multiple analytic band-pass filter” was presented by some scholar and used into demodulation analysis [22], it constructed an ideal function from the point of filter. The expression of the impulse response of the analytic filter is

  (15)

The real and the imaginary parts of this complex function can be expressed as

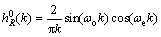                  (16)

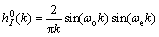                  (17)

where ω_e is the complex frequency shifting quantity, 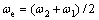; ω_o is the cut-off frequency of the low pass filter,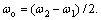Here ω₁ and ω₂ are the pass-band lowest frequency and highest frequency. Substituting ω_o and ω_e into expressions (16) and (17), gives

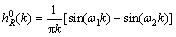               (18)

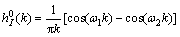               (19)

Compared these two equations with the expression (9), it can be found that this multiple analytic filter is the NEWLAND’s harmonic wavelet function. Their characteristic of frequency domain and time domain are completely consistent.

3.3 Advantage of harmonic wavelet transform

Compared with Eqs. (18) and (19), it can be seen that the variable of expression (11) to (14) is transformed, and the variable possesses the ability of alterable analysis range. That is to say, the harmonic wavelet transform has the ability of adjustable resolution of time-frequency window.

But for multiple analytic band-pass filter, it needs to add window function to improve the flat degree of pass band and the ripple effect of cut-off band when processing the band-pass filter. The so-called demodulation in analyzing unstable dynamic signal is just to do the process: determine the range of band pass according to the center position of the signal, carry through the band-pass filter, and windowing to improve the band-pass effect. It is obvious that the multiple analytic band-pass filter does not have the ability of adjusting resolution of time-frequency window.

4 Establishment of adaptive harmonic window and its comparison

As analyzed in the previous section, the filter function is used in windowing analysis, so the filter is the component of the window function. But only by filtering, the unstable signal can not be well analyzed. Since the wavelet analysis method possesses the ability of adjusting resolution of time-frequency window, it has already become a useful method for analyzing unstable signal. But for the dyadic wavelet transform, which based on the binary, there are some problems in their decomposition [18]. For harmonic wavelet, though the problems can be settled by proper reformation, but it is still decomposed according to each layer.

The m, n in time-frequency equations (13) or (14) determined the decomposed layer of the wavelet transform, just like the role of j in expression 2^–j in the dyadic wavelet transform. Concretely, if f_h is the highest analysis frequency, then

                (20)

Obviously it can be seen that: n≥m. In harmonic wavelet transform, supposing that

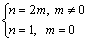                             (21)

then in the Eq. (20), if m=2^－jf_h , then n=2m=2^1－jf_h.

Supposing that m=0 alike, then according to the Eq. (20), we have

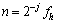, m=0                             (22)

Or supposing that n=f_h, then according to the Eq. (20), it can be got that

                             (23)

As can be seen from the above three cases, along with the increase of the decomposed layer, the analysis range in frequency domain will be narrowed, but there are some frequency ranges will not be found in the same decomposed layer, i.e., only a part of the signal and frequency range will be obtained after decomposition. This transform characteristic is the same as the dyadic wavelet transform (but more flexible than the dyadic wavelet transform).

In the harmonic wavelet analysis, NEWLAND [20] presented the wavelet’s frequency ranges in each layer, the characteristic is that: along with the increasing of decomposed layers, the frequency range of analysis will gradually tend to be high frequency. There will also some frequency ranges that could not be obtained in the same decomposed layer by NEWLAND analysis method.

Above selections gave the reasonable value of m and n. But the decomposition result given in above conditions still could not include every interested frequency ranges, i.e., it can not realize the function of decomposing at any frequency range. This causes the difficulties in arbitrary frequency band selection when analyzing signal.

Releasing the restriction about 2^－jin the value scope of m, n, and redefining the range of m, n: m, n∈R⁺ and m

                               (24)

where 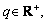B is the width of the frequency range for analysis.

By programming the harmonic wavelet function, a new window function is established, which can be named as adaptive harmonic window. Any frequency range can be extracted by adaptively moving the window to that frequency range, and then only selecting B and q which confirmed by Eq. (24) for analysis. So the trigonometric expression of adaptive harmonic window function can be given as below:

,

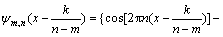
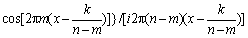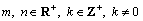                (25)

Its conjugated expression is

           (26)

Now, it can be seen that adaptive harmonic window transform is terse, intuitional, and easy to achieve，and also can avoid the problems existed in the dyadic wavelet decomposition. The problems are that the data size and frequency range will be halved along with the decomposition in each layer, and so will the sampling frequency be reduced to half. Then the detail signal is distorted, accompanying with the wavelet decomposition in every layer.

Due to the admirable flat top shape and box characteristic of harmonic wavelet, the adaptive harmonic window function has good performance for leakage restraining. Figures 4 and 5 show the comparative characteristic of Hanning window function and adaptive harmonic window function in time domain and frequency domain. Usually Hanning window can do better in dealing with the leakage of the signal analysis, especially for the vibration signal. It can be seen from the figures that although Hanning window has good characteristic, but due to its relatively great side lobe effect, its performance is not good compared with adaptive harmonic window.

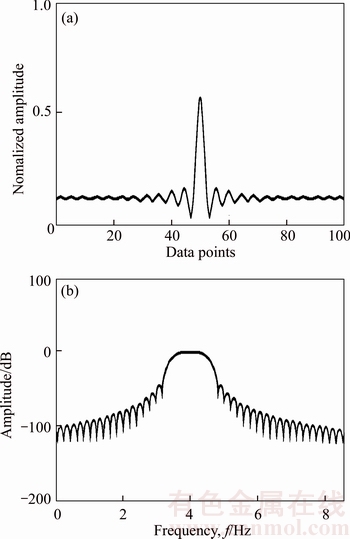
Figure 4 Characteristic of Hanning window function in time-frequency domain

Figures 4 and 5 only give the adaptive harmonic windows ability of leakage restraining. The more outstanding characteristic is that it has the advantage of harmonic wavelet decomposition in the frequency domain, and can be expanded for analysis at any frequency range.

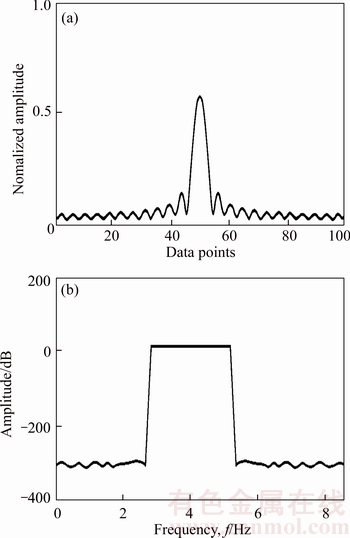
Figure 5 Characteristic of adaptive harmonic window function in time-frequency domain

5 Application of adaptive harmonic window

5.1 Simulation analysis of frequency extraction under strong background noise

For digital signal

f(x)=5sin(2π f x/f_s)+n(x) (x =0, 1, 2, …, 2047)     (26)

In the signal, f=390 Hz, f_s=1024 Hz, analysis frequency f_h=f_s/2, n(x) is the input white noise, and n(x)~NID(0, 20²). As shown in Figure 6(a), it can be analyzed by using adaptive harmonic window. The window center takes q=24 and the window width takes B=16 Hz. Then the window frequency range lies between 384 Hz to 400 Hz and the frequency center is 392 Hz. The analytical results are shown in Figures 6(b) and (c). It is obvious that the noise signal has been greatly restrained, and the frequency’s component has been more prominence. For the reconstructed signal in time domain, the noise is substantially eliminated, and the mainly periodic signal is retained. It can be seen that, owing to that the weak periodical signals are entirely submerged by noise, the spectrum of the signal in analysis range and the reconstructed wave form in time domain can not be obtained by routine methods. By using usual STFT, the spectrum can not be got at this not so higher frequency point. Figure 6(d) shows the filtering result by FIR band-pass filter in the same range. It can be seen from Figure 6(d) that the stop-band leaks is seriously, and the energy intersperse among the whole frequency domain [23].

Figure 6 Frequency extraction and time domain reconstruction of weak periodic signal under strong background noise:

It should be pointed out again that whatever choosing the method of band-pass filter or the windowing analysis, the object is to separate the interested frequency for analysis, and it can not confuse the concepts and methods in band-pass filter and windowing analysis.

5.2 Rotor orbit purification in high frequency

The rotor fault symptom of high-speed rotating equipment is often occurred in high frequency band first. So the fault feature frequency is particularly important. For the extraction of axis orbit in different frequency bands from the rotor system, many aspects have been researched, and satisfactory effects have been achieved [24]. But the previous studies mainly focused on low frequency band. Low frequency band of the orbit is obvious, and the extraction of axis orbit is relatively easy. For high frequency (>500 Hz), the intensive spectrum peak is usually along with strong noise which is difficult to extract the fault feature frequency by using conventional methods, including narrow band filtering and windowing processing. That will result in the difficulty for extracting fault feature of rotor. Especially, when there are two or more close frequency characters of rotor, it is hard to get one of rotor axis orbits in the corresponding frequency peak.

Adaptive window function based on the harmonic wavelet can position the window region in the interesting frequency range, and reflect the local vibration characteristics of rotor. Therefore, the adaptive window can satisfy the complex extraction of axis orbit in high frequency range, even recovery the time waveform features of the axis orbit.

The time domain vibration waveform of a high-speed rotor steady operation is shown in Figure 7(a). The waveform picture is quite complex, the vibration characteristics can not be seen. The frequency characteristic of FFT in high frequency range is also difficult to distinguish clearly, as seen in Figure 7 (b).

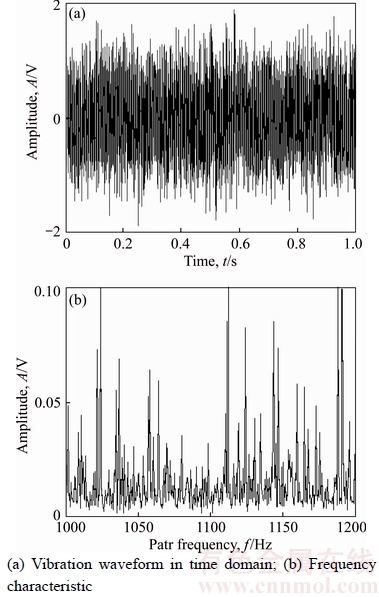
Figure 7 Vibration signal of a high-speed rotor:

In Figure 7(b), there are two adjacent spectrum peaks, respectively in the vicinity of 1023 Hz and 1025 Hz. On the same section of rotor, sample along two directions x, y. For this high frequency signal, the sampling frequency is set up as f_s=4096 Hz to get the sampled data. Set the window width B=4 Hz. Corresponding two high frequency peaks 1023 Hz and 1025 Hz, two centre position q=255, 256 will be automatically obtained by adaptive window control program, the window positions are between 1020 Hz to 1024 Hz and between 1024 Hz to 1028 Hz.

Using adaptive harmonic window to analyze these sampling signals on two directions of x, y, it can automatically extract 4 Hz narrow band data. That will remove the most part of noise. Then two time domain signals are reconstructed in this narrow band. The shaft orbits of two frequency bands are shown in Figures 8(a) and (b). It can be seen that the orbit obtained is a clear elliptic, no need for additional purification. So it provides convenient conditions for the fault analysis of high speed rotor.

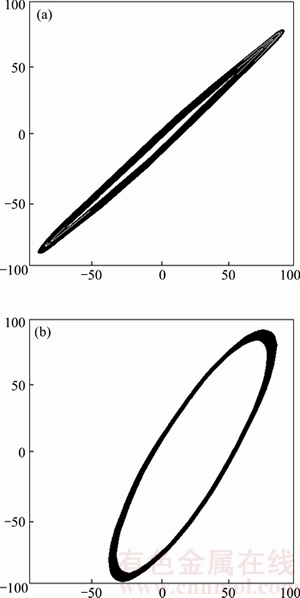
Figure 8 Rotor orbit purification in the vicinity of 1023Hz and 1025Hz

It should be emphasized that this designed program of adaptive window can avoid the spectrum peak to fall on the window boundary for preventing unsatisfactory analysis results. For the intensive spectrum peaks in high frequency, a very narrow window is required. The designed program of adaptive harmonic window ensures this requirement.

6 Conclusions

1) Through theoretical analysis, it is demonstrated that the multiple analytic band-pass filter has consistency with harmonic wavelet base function, and their research and application are unified. In demodulation analysis, multiple analytic band-pass filter can achieve the effect of band pass filtering but can be difficult to adaptively extract the period signal from strong noise.

2) Adaptive harmonic window function proposed in this work has good performance of restraining leakage compared with Hanning window function, and its analysis center can be moved easily and its scale can be changed freely, and can extract period signal from strong noise conveniently.

3) Adaptive harmonic window is the development of wavelet analysis technique, and also the expansion and enrich of the content and application advantage of window function.

4) Applying the adaptive harmonic window function, the frequency extraction of weak signal under strong noise is achieved. Compared with other methods, the adaptive harmonic window shows its advantage in weak signal extraction.

5) The shaft orbits of high frequency under strong noise in high-speed rotating equipment are successfully purified using adaptive harmonic window. This shows that the adaptive harmonic window can be successfully applied to practical engineering in the signal processing.

References

[1] HEYDT G, FJELD P, LIU C. Applications of the windowed FFT to electric power quality assessment [J]. IEEE Transactions on Power Delivery, 1999, 14(4): 1411–1416. DOI: 10.1109/61.796235.

[2] FREDRIC J. On the use of windows for harmonic analysis with the discrete Fourier transform [J]. Proceedings of the IEEE, 1978, 66: 51–83. DOI: 10.1109/PROC.1978.10837.

[3] NUTTALL A. Some windows with very good sidelobe behavior [J]. IEEE Transactions on Acoustics Speech & Signal Processing, 1989, 29(1): 84–91. DOI: 10.1109/ TASSP. 1981.1163506.

[4] HA Y, PEARCE J. A new window and comparison to standard windows [J]. IEEE Transactions on Acoustics Speech & Signal Processing, 1989, 37(2): 298–301. DOI: 10.1109/29.21693.

[5] ZOU Mu-yan, LIU Rei-rong. I₁-csch window function and its application [J]. ACATA Electronica Sinica, 1985, 13: 85–92. http://www.springer.com/engineering/ electronics/ journal/11767.

[6] ZHANG Jie-qiu, LIANG Hong-chang, CHEN Yan-pu. A new family of windows—convolution windows and their applications [J]. Scientia Sinica Techologica, 2005, 48(4): 461–481. DOI: 10.1360/03ye0531.

[7] WEN He, TENG Zhao-sheng, GUO Si-yu. Hanning self convolution window function and its application of harmonic analysis [J]. Scientia Sinica Techologica, 2009, 52(2): 467–476. DOI: 10.1007/s11431-008-0356-6.

[8] STUART W, ANDREAS A. Design of ultraspherical window functions with prescribed spectral characteristics [J]. EURASIP Journal on Applied Signal Processing, 2004, 13: 2053–2065. DOI: 10.1155/S1110865704403114.

[9] AVCI K, NACAROG L. A cosine hyperbolic window family with its application to FIR filter design [C]// International Conference on Information and Communication Technologies: From Theory to Applications IEEE. 2008: 1–6. DOI: 10.1109/ICTTA. 2008.4530047.

[10] AVCI K, NACAROG L. Modification of cosh window family [J]. International Journal of Electronics and Communications, 2009, 63: 907–916. DOI: 10.1109/ ICTTA.2008.4530048.

[11] MOTTAGHI M, SHAYESTEH M. New efficient window function, replacement for the hamming window [J]. Signal Processing Iet, 2011, 5(5): 499–505. DOI: 10.1049/iet-spr.2010.0272.

[12] WEN He, TENG Zhao-sheng, GUO Si-yu. Triangular self-convolution window with desirable sidelobe behaviors for harmonic analysis of power system [J]. IEEE Transactions on Instrumentation and Measurement, 2010, 59(3): 543–552. DOI: 10.1109/ TIM.2009.2024702.

[13] ROHIT P, KUMAR M, JAISWAL A, SAXENA R. Design technique of bandpass FIR filter using various window function [J]. IOSR Journal of Electronics and Communication Engineering (IOSR- JECE), 2014, 6(6): 52–57. DOI: 10.9790/2834-0665257.

[14] XIAO Ying, FENG Chang-jian. A time-frequency representation method of STFT with combining window functions [J]. Journal of Detection& Control, 2010, 32: 43–47. DOI: 10.3969/j.issn.1008-1194.2010.03.011.

[15] LI Shun-ming. On phase holding by dyadic wavelet double transform in vibration signal detects [J]. Chinese Journal of Scientific Instrument, 2005, 26: 370–373. DOI: 10.3321/ j.issn: 0254-3087.2005.04.010. (in Chinese)

[16] D'HEEDENE S, AMARATUNGA K, CASTRillón-candás J. Generalized hierarchical bases: a wavelet-ritz-galerkin framework for Lagrangian FEM [J]. Engineering Computations: International Journal for Computer-Aided Engineering and Software, 2005, 22(1): 15–37. DOI: 10.1108/02644400510572398.

[17] WIESLAW J, STASZEWSKI D, MARK W. Wavelet-based frequency response function for time-variant systems—An exploratory study [J]. Mechanical Systems and Signal Processing, 2014, 47(1, 2): 35–49. DOI: 10.1016/j.ymssp. 2013.03.011.

[18] LI Shun-ming. Harmonic wavelet packet method and used on accurate obtaining the orbit of rotor sub-frequency signal [J]. Chinese Journal of Mechanical Engineering, 2004, 40: 133–137. DOI: 10.3901/JME. 2004. 09.133. (in Chinese)

[19] ZHANG Xian-da, BAO Zheng. Non-stationary signal analysis and processing [M]. Beijing: National Defence Industry Press, 1998. http://www.ndip.cn/. (in Chinese)

[20] NEWLAND D. Harmonic wavelet analysis [J]. Proceedings of the Royal Society A Mathematical Physical & Engineering Sciences, 1993, 443(443): 203–225.

[21] NEWLAND D. An introduction to random vibrations, spectral and wavelet analysis, 3rd Edition [M]. New York: Longman, Harlow and John Wiley, 1993: 359–370. http:// www.logobook.kz/prod_show.php?object_uid=11168166.

[22] DING Kang, XIE Ming, ZHANG Bi-de, ZHAO Ling. Multiple analytic band-pass filter and its application in demodulation analysis [J]. Journal of Vibration Engineering, 2000, 13: 385–392. DOI: 10.16385/j.cnki.issn.1004-4523. 2000.03.009. (in Chinese)

[23] ZHANG Pei-yao, MA Xiao-jiang, WANG Ji-jun, ZHU Hong. Wavelet packet signal extraction algorithm and its application in fault diagnosis [J]. Journal of Dalian University of Technology, 1997, 39: 67–72. http://en.cnki. com.cn/Article_en/CJFDTOTAL-DLLG701.016.htm, 1997- 01/. (in Chinese).

[24] PENG Zhi-ke, HE Yan-zao, CHEN Zhi-yong, CHU Fu-lei. Identification of the shaft orbit for rotating machines using wavelet modulus maxima [J]. Mechanical Systems and Signal Processing, 2002, 16(4): 623–635. DOI: 10.1006/mssp.2002.1494.

(Edited by HE Yun-bin)

中文导读

自适应谐波窗及其在振动信号频率提取中的应用

摘要：本文研究的目标在于寻找一个自适应的优秀窗函数，来提取强噪声下微弱振动信号和高频段的振动信号。首先分析了加窗变换与滤波的关系，介绍了小波变换具有可变时频窗的优势。其次分析了谐波小波与复解析带通滤波器的关系，指出了复解析带通滤波器与谐波小波基函数的一致性，发现了谐波小波变换对复解析带通滤波器的包含性。然后对谐波小波变换进行拓展，提出了不需要进行分层分解的自适应谐波窗的概念与理论表达式。通过与汉宁窗对比，分析了自适应谐波窗极其优秀的抑制泄漏能力，和时频窗分析中心自由移动和任意改变尺度的优秀特性。最后将所提出的自适应谐波窗应用到高速转子的强噪声下微弱周期信号的频率提取，和高频轴心轨迹的提取中，取得了满意的效果。该应用效果显示出自适应谐波窗函数能够成功应用于实际工程信号处理中。

关键词：窗函数，傅立叶变换，滤波器，谐波小波，自适应，振动信号提取

Foundation item: Project(51675262) supported by the National Natural Science Foundation of China; Project(6140210020102) supported by the Advance Research Field Fund Project of China; Project(2016YFD0700800) supported by the National Key Research and Development Plan of China

Received date: 2016-04-05; Accepted date: 2017-12-01

Corresponding author: LI Shun-ming, PhD, Professor; Tel: +86-13605199671; E-mail: smli@nuaa.edu.cn, 2542670528@qq.com; ORCID: 0000-0002-1271-6036