铁矿石烧结过程传热传质数值模拟
张小辉,张家元,张建智,苏浩,周孑民
(中南大学 能源科学与工程学院,湖南 长沙,410083)
摘要:铁矿石烧结是一个复杂的传热传质过程,包括各相之间的传热、水的蒸发与冷凝、碳燃烧、石灰石分解、矿石熔化与凝固以及气相反应等方面。通过对烧结过程进行研究,以多孔介质模型为基础,结合局部非热力学平衡的能量双方程模型、组分传输模型和烧结反应动力学模型,以FLUENT软件为计算平台,采用自定义标量(UDS)构建能量双方程模型,采用自定义功能(UDF)对能量方程、组分传输方程的源项进行修正和定义,建立铁矿石烧结过程传热传质的三维非稳态计算模型。利用该模型对烧结过程进行数值模拟,得到气、固温度以及主要烟气成分的分布,通过与测试值的对比来验证模型的可靠性。
关键词:烧结;传热;传质;反应动力学;数值模拟
中图分类号:TF046.4 文献标志码:A 文章编号:1672-7207(2013)02-0805-06
Numerical simulation of heat and mass transfers in sintering process
ZHANG Xiaohui, ZHANG Jiayuan, ZHANG Jianzhi, SU Hao, ZHOU Jiemin
(School of Energy Science and Engineering, Central South University, Changsha 410083, China)
Abstract: Iron ore sintering is a complex process of heat and mass transfers, which contains heat transfers in/between each phase, water evaporation and condensation, coke combustion, limestone decomposition and gaseous reaction. Through researching the iron ore sintering process, a 3D-unsteady mathematical model was developed. This model was based on the porous media model and combined the portion non-equilibrium thermodynamics energy two-equation model, species transport and sintering reaction kinetic models. This model was conducted on the platform of FLUENT software, the energy two-equation model was established through the user defined scalars (UDS), and the source terms of energy equations and species transport equations are corrected through the user defined functions (UDF). The temperature of gas and solid and the distribution of major gas components can be obtained by using this model to simulate the sintering process. The simulation results and the experimental results are agreed well, which shows that the model is reliable.
Key words: sintering; heat transfer; mass transfer; reaction kinetic; numerical simulation
将铁矿粉与石灰石、燃料等混合后进行烧结造块的过程中,会发生一系列复杂的物理化学反应,这些物理化学反应均伴随着传热和传质[1-3],在这一过程中,烧结矿的温度与这些反应互相影响。目前,对于烧结传热过程的研究主要集中在对烧结料层温度的准确预测以及烧结终点的判断[4-5],而计算过程多是进行相应的简化。夏德宏等[6]对烧结过程碳燃烧与传热过程建立数学模型,进行数值模拟,并开发出可视化软件。但是,该模型只考虑碳的燃烧。龙红明等[7]对烧结过程中各层分别建立传热方程即分段计算模型,对烧结料层温度进行模拟计算,但实际的烧结过程是连续的,该模型也没有考虑点火、保温阶段以及燃烧带可能发生碳的不完全燃烧反应,而这种反应是烟气中含有CO的主要原因。Yang等[8-9]建立一维非稳态的计算模型,考虑气固之间的对流、传热以及辐射,子模型包含气固反应、气体反应以及孔隙率的变化。作者利用这一模型对不同碳质量分数、不同抽风量的工况进行优化模拟。Tan等[10]针对烧结过程建立包含有15个物理化学反应的计算流体力学计算模型,用以对烧结过程二恶英的产生进行研究,但是,该研究没有考虑石灰石的分解对料层温度及废气成分的影响。为此,本文作者以局部非热力学平衡理论和组分传输理论为基础,结合烧结过程中各反应的动力学方程,全面考虑烧结过程中的反应以及这些反应对于传热和传质的影响,建立三维非稳态计算模型,对烧结传热和传质过程进行研究。
1 模型的建立
对于气体流过料层时所产生的压力降,采用多孔介质模型来计算[11-12]。对于多孔介质条件下所产生的动量方程附加源项采用Ergun公式进行修正[12-13]。
1.1 传热模型
对于计算单元内气、固温度的求解采用局部非热力学平衡双能量方程[13-14]模型,分别建立能量方程,通用方程组[15-16]如式(1)和(2)所示。
固相:
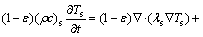
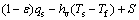 (1)
(1)
气相:
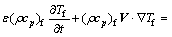
 (2)
(2)
其中:ε为料层孔隙率;Ts和Tf分别为固、气温度,K;qs和qf分别为固、气内热源,W/m3;S为反应热, ;Ri为烧结过程各种反应的反应速率,mol/(m3×s);△Hi为相应反应的反应热,J/mol;hv为气、固之间体积传热系数,W/(m3×K),可利用Achenbach准则关系式[17]计算,即
;Ri为烧结过程各种反应的反应速率,mol/(m3×s);△Hi为相应反应的反应热,J/mol;hv为气、固之间体积传热系数,W/(m3×K),可利用Achenbach准则关系式[17]计算,即
 (3)
(3)
其中:hp为气、固传热系数,W/(m2×K);dp为固体粒径,m。
1.2 组分传输模型
组分输运方程[18]如下:
 (4)
(4)
其中:Ji为质量扩散,在湍流中,Ji=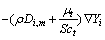 ;Ri为单位容积的组分的生成率;Si为离散相的额外反应速率。
;Ri为单位容积的组分的生成率;Si为离散相的额外反应速率。
1.3 烧结过程反应动力学模型
烧结过程所发生的物理化学反应主要有物料的干燥、碳燃烧、石灰石分解、铁矿石的融化及凝固[11]等。
1.3.1 物料干燥
对于物料的干燥(水分蒸发,即(H2O)l=(H2O)g)过程,考虑2个阶段:恒速干燥阶段和减速干燥阶段。这2个阶段以物料的含水量是否达到临界含水量为标准[17]。
当料层含水量大于临界值时,处于恒速干燥阶段。此时由上层气体传递的热量完全用于水的蒸发,认为Ts为一定值。这一阶段的干燥速率为:
 (5)
(5)
其中:a为颗粒与床层的比表面积,m-1;△H1为水的汽化潜热,J/kg;Mw为水相对分子质量。
当料层含水量小于临界值大于平衡值时,处于降速干燥阶段,此时由上层气体传递的热量用于固体颗粒温度的升高和水的汽化潜热。在烧结高温条件下,达到平衡含水量时已非常接近干燥状态,因此,将这一阶段适当简化,视平衡含水量为0,这一阶段的干燥速率为:
 (6)
(6)
其中:w和wc分别为含水质量分数、临界含水质量分数。
1.3.2 碳反应
在烧结过程中,碳的反应[10]有:C+O2=CO2,C+CO2=CO,C+H2O=CO+H2。
对于C+O2=CO2,反应速率[19]为:
 (7)
(7)
其中:rc为碳颗粒粒径,m; 为氧气的浓度,mol/m3;Nc为单位体积内燃料颗粒数;
为氧气的浓度,mol/m3;Nc为单位体积内燃料颗粒数;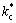 为综合反应速率常数,计算式如下:
为综合反应速率常数,计算式如下:
 (8)
(8)
其中:kf,1为传质系数,m/s;k1为反应速率常数,m/s。
对于C+CO2=CO,反应速率[19]为:
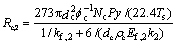 (9)
(9)
其中:fc为燃料颗粒形状系数;P为料层内压力;y为烟气中CO2体积分数;Ef,2为反应有效系数;kf,2为界膜传质系数,m/s;k2为反应速率常数,m3/(kg×s)。
对于C+H2O=CO+ H2,反应速率[19]为
 (10)
(10)
其中:u为烟气中水蒸气体积分数;kf,3为界膜传质系数,m/s;Ef,3为反应有效系数;k3为反应速率常数,m3/(kg×s)。
1.3.3 石灰石分解
石灰石的分解反应不受内扩散限制,烧结料层中气流速度快,外扩散阻力较小,可以认为反应是处于化学反应的控制范围之内,反应速度主要受温度的影响。根据热平衡,石灰石分解反应速率[3]为:
 (11)
(11)
其中:al为石灰石颗粒比表面积,m-1;Tl为分解开始温度,K;Ul为与分解度相关的系数。
1.3.4 铁氧化物的反应
烧结过程中主要发生铁的氧化物的还原反应,铁矿石主要成分不同,其所发生的反应也不同。这里以赤铁矿为例。根据文献[19],主要发生的反应为:Fe2O3+3CO=2Fe+3CO2,Fe2O3+3H2=2Fe+3H2O。
对于Fe2O3+3CO=2Fe+3CO2,反应速率为:
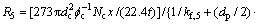
 (12)
(12)
其中:kf,5为界膜传质系数,m/s;x为烟气中CO体积分数;fs为铁矿石还原度;k5为反应速率常数,m/s;K5为反应平衡常数。
对于Fe2O3+3H2=2Fe+3H2O,反应速率为:
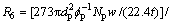
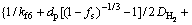
 (13)
(13)
其中:kf,6为界膜传质系数,m/s;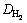 为H2分子扩散系数,m2/s;k6为反应速率常数,m/s;K6为反应平衡常数。
为H2分子扩散系数,m2/s;k6为反应速率常数,m/s;K6为反应平衡常数。
1.3.5 液相形成与凝固
根据文献[20],烧结过程中液相形成速率为:
 (14)
(14)
凝固速率为:
 (15)
(15)
其中:Tmlt为开始熔化(凝固)温度,K。
1.3.6 其他气相反应
气相中含有少量生成的H2,在高温区与O2反应:H2+O2=(H2O)g,反应速率[20]为:
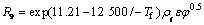 (16)
(16)
其中:φ为烟气中H2体积分数。
在高温区还会发生水煤气转化反应CO+H2O= CO2+H2,反应速率[19]为:
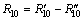 (17)
(17)
其中:
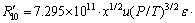
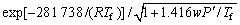 (18)
(18)
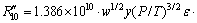
 (19)
(19)
其中:R为气体常数,J/(mol×K)。
2 模型的求解
以上模型基于FLUNT计算平台建立和求解。对气体流过烧结矿时由黏性阻力和惯性阻力引起的附加动量源项[21],利用Ergun公式计算黏性阻力系数和惯性阻力系数[13];对于基于局部非热力学平衡双能量方程所建立的气、固两相能量方程,首先利用自定义标量(UDS)分别定义Ts和Tf,然后结合以上反应的动力学方程,利用自定义功能(UDF)功能对能量方程的源项分别在不同的温度条件下进行定义;对于烧结废气成分的模拟基于组分输运和有限速率化学反应模型,基于UDF功能同时结合以上反应的反应速率分别进行定义。
用于该计算模型的参数及初始值如表1所示,部分参数的取值参考涟钢360 m2烧结机实际操作参数。
由于烧结的传热传质是非稳态过程,因此,在求解过程中,根据所处阶段的不同调整边界条件,在点火、保温、烧结阶段,调整入口风量、风温;对于传热计算,碳颗粒燃烧的温度条件为923 K,石灰石分解的温度条件为993 K。铁矿石开始熔化及凝固温度为1 473 K。其他在本文中所用到的参数及计算式如表2所示。
表1 计算参数初始值
Table 1 Initial value of simulation parameters
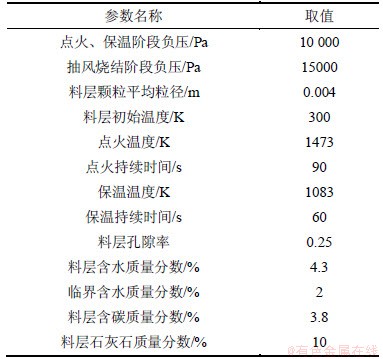
表2 计算模型所用到的参数
Table 2 Parameters in simulation model

3 计算结果及分析
利用以上所建立的模型进行铁矿石烧结传热传质的模拟计算,图1所示为不同料层高度处烧结料层与气体温度变化情况。料层高度以料面为起点计算,由图1可知:在气体温度达到最高点之前,同一点处的气体温度大于固体温度,此时气体向固体传热,加热料层并使燃料燃烧;随着料层中燃料的快速燃烧,固体温度超过气体温度,此时固体向气体传热,随着燃烧的完成,由上而下的气流对料层进行冷却;由于蓄热作用,烧结速度逐渐加快,并且料层最高温度逐渐增加。
图2所示为烧结料层在整个烧结过程中的温度分布情况。由图2可见:料层最高温度在前700 s偏低,在700 s之后由于料层的蓄热作用,最高温度逐渐升高,同时高温带的厚度不断增加。
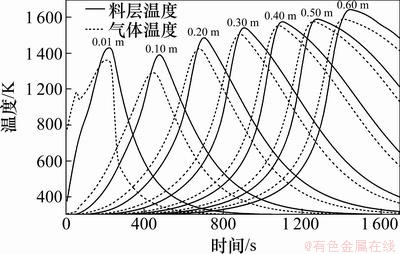
图1 不同高度处气、固温度
Fig.1 Gas and solid temperatures in different heights
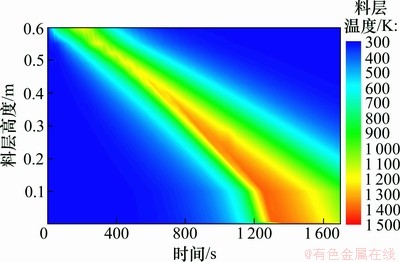
图2 烧结料层温度分布
Fig.2 Temperature distribution of sinter
图3所示是从点火到烧结完成整个过程中料层最高温度以及计算域出口处的气体温度的变化趋势。固体温度的测点沿台车高度等距离分布, 即在0.6 m料层高度上平均分布6个测点,从点火开始每60 s取1次值,测量3次,将每1点处测得的固体温度值进行平均,然后取6个点的最大值。气体温度的测点设在位于台车下部的风箱入口处,每个风箱设1测点,取5次测量平均值作为每1风箱的气体平均温度。
从图3可见:保温段结束之后固体料层最高温度下降约80 K,之后又稳定上升,时间从240 s持续到400 s左右,可称为“过渡阶段”。这一固体最高温度降低的阶段发生在离料面约0.04~0.1 m的高度范围内,这一阶段最高温度的突降,是由进入料层气流的温度突降和流量增加所引起。在整个烧结过程中料层温度最高点位于倒数第2个风箱位置左右,此后料层温度下降,因此,可以认为此时整个料层的烧结反应结束,料层温度达到最高点时烧结台车所处的位置可认为是烧结终点位置。
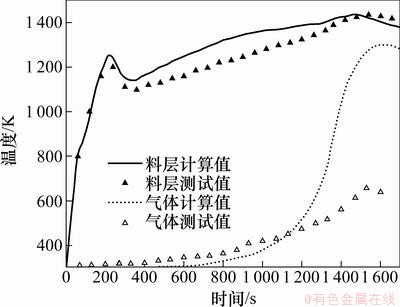
图3 烧结过程中气、固温度变化曲线
Fig.3 Temperature curves of solid and gas in sintering process
由图3可见:对于台车底部废气温度的变化,在1 200 s之前,出口处的气体温度上升缓慢,在烧结反应接近料层底部的时候,气体温度迅速上升,气体温度达到最高点的位置与料层温度达到最高点的位置接近,因此,烧结台车废气温度达到最高点的位置也可以作为烧结终点位置的判断标准。由于风箱中气流温度是几个台车底部气流的混合,故测量值与达到烧结终点时台车底部气流温度相差较大,但是,温度发展趋势与计算结果一致。
图4所示为料层底部出口处气体成分体积分数在烧结过程中的变化以及与实测值的比较。测点分布于台车下部的各风箱入口处,与废气温度的测量共用测点。由水蒸气含量的变化可知在点火启动之后,出口处水蒸气体积分数快速上升,之后在保温阶段完成时达到平稳状态;随着气体及烧结料层温度的不断上升,料层含水量不断减少,出口气体中水蒸气体积分数也逐渐减小在1 000 s时开始减小,在1 200 s左右料层水分蒸发完毕。由O2,CO和CO2体积分数的变化可知,在点火和保温阶段,从料面到离料面0.04 m的高度内温度高,在短时间内快速发生上述一系列物理化学反应,而该阶段内抽风负压小,气体流量小,故前240 s这3种气体体积分数变化较大,O2快速减少,而CO和CO2快速增加;在保温阶段后,气体成分趋于稳定,在烧结前沿到达离料面约0.55 m处时,O2,CO和CO2的体积分数又逐渐恢复到与入口处的浓度达到一致的水平。
图3和图4中计算值与测试值的对比可知,计算值与测试值吻合较好,说明该模型在预测烧结过程的气、固温度变化以及烧结废气成分上是可靠的。
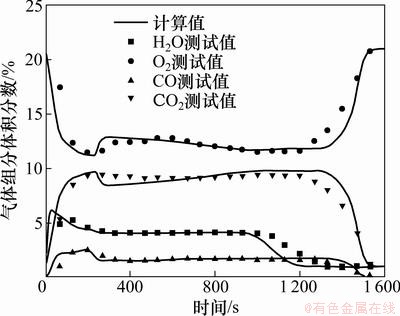
图4 出口处气体组分体积分数
Fig.4 Volume concentrations of gas composition in outflow
4 结论
(1) 通过对铁矿石烧结过程传热传质的研究,结合多孔介质模型、k-ε湍流模型、基于局部非热力学平衡的双方程能量模型、组分输运模型以及化学反应动力学模型,以FLUENT软件为计算平台,利用UDF和UDS功能,建立了烧结过程传热传质的数学计算模型。
(2) 利用所建立的模型对烧结过程气、固温度以及废气成分进行计算和分析,通过与测试值的比较,证明了该模型的可靠性。研究结果表明:在点火到正常抽风烧结的“过渡阶段”, 在离料面0.04~0.1 m的高度范围内,烧结矿最高温度降低约80 K,烧结速度减慢,导致出口处气体成分发生相应突变。
(3) 利用该模型可以模拟计算在不同配炭比、不同点火及烧结条件下的传热传质过程,并对烧结过程的控制、废气成分的控制以及烧结终点的预测有指导意义。
参考文献:
[1] Yang W, Choi S, Choi E S, et al. Combustion characteristics in an iron ore sintering bed: Evaluation of fuel substitution[J]. Combustion and flame, 2006, 145(3): 447-463.
[2] Sadrnezhaad S K, Ferdowsi A, Payab H. Mathematical model for a straight grate iron ore pellet induration process of industrial scale[J]. Computational Materials Science, 2008, 44(2): 296-302.
[3] 张玉柱, 艾立群. 钢铁冶金过程的数学解析与模拟[M]. 北京: 冶金工业出版社, 1997: 95-107
ZHANG Yuzhu, AI Liqun, Mathematical analysis and simulation of metallurgical process[M]. Beijing: Metallurgical Industry Press, 1997: 95-107.
[4] Mitterlehner J, Loeffler G, Winter F, et al. Modeling and simulation of heat front propagation in the iron ore sintering process[J]. ISIJ International, 2004, 44(1): 11-20.
[5] 张家元, 李黎, 张小辉. 基于数值模拟的烧结终点在线控制[J]. 烧结球团, 2011, 36(3): 5-9.
ZHANG Jiayuan, LI Li, ZHANG Xiaohui. On-line control of burning through point based on numerical simulation[J]. Sintering and Pelletizing, 2011, 36(3): 5-9.
[6] 夏德宏, 焦红蕾, 张刚, 等. 烧结工序中燃烧与传热过程的数值模拟[J]. 工业炉, 2006, 28(3): 30-32.
XIA Dehong, JIAO Honglei, ZHANG Gang, et al. Numerical simulation of combustion and heat transfer in sintering process[J]. Industrial Furnace, 2006, 28(3): 30-32.
[7] 龙红明, 范晓慧, 毛晓明, 等. 基于传热的烧结料层温度分布模型[J]. 中南大学学报: 自然科学版, 2008, 39(3): 436-442.
LONG Hongming, FAN Xiaohui, MAO Xiaoming, et al. Sintering bed temperature distribution model based on heat transfer[J]. Journal of Central South University: Science and Technology, 2008, 39(3): 436-442.
[8] Yang W, Ryu C, Choi S, et al. Mathematical model of thermal processes in an iron ore sintering bed[J]. Metals and Materials International, 2004, 10(5): 493-500.
[9] Yang W, Ryu C, Choi S, et al. Modeling of combustion and heat transfer in an iron ore sintering bed with considerations of multiple solid phases[J]. ISIJ International, 2004, 44(3): 492-499.
[10] Tan P, Neuschütz D. CFD modeling of sintering phenomena during iron ore sintering[C]//Multiphase Phenomena and CFD Modeling and Simulation in Materials Processes. Charlotte: TMS, 2004: 451-459.
[11] Li H G, Zhang J L, Pei Y D, et,al. Melting characteristics of iron ore fine during sintering process[J]. Journal of Iron and Steel Research, 2011, 18(5): 11-15.
[12] 张家元, 张小辉, 周孑民, 等. 烧结矿冷却过程正交模拟优化试验研究[J]. 钢铁, 2011, 46(7): 86-89.
ZHANG Jiayuan, ZHANG Xiaohui, ZHOU Jiemin, et al. Optimal orthogonal simulation research of sinter cooling[J]. Iron and Steel, 2011, 46(7): 86-89.
[13] 张小辉, 张家元, 戴传德, 等. 烧结矿冷却过程数值仿真与优化[J]. 化工学报, 2011, 62(11): 3081-3087.
ZHANG Xiaohui, ZHANG Jiayuan, DAI Chuande, et al. Optimal and simulation of sinter cooling process[J]. CIESC Journal, 2011, 62(11): 3081-3087.
[14] 刘伟, 范爱武, 黄晓明. 多孔介质传热传质理论与应用[M]. 北京: 科学出版社, 2006: 28-32.
LIU Wei, FAN Aiwu, HUANG Xiaoming. Porous media theory and application of heat and mass transfer[M]. Beijing: Science Press, 2006: 28-32.
[15] Alazmi B, Vafai K. Analysis of fluid flow and heat transfer interfacial conditionsbetween a porous medium and a fluid layer[J]. International Journal of Heat and Mass Transfer, 2001, 44(9): 1735-1749.
[16] 李菊香, 涂善东. 考虑局部非热平衡的流体层流横掠多孔介质中恒热流平板的传热分析[J]. 化工学报, 2010, 61(1): 10-14.
LI Juxiang, TU Shandong. Heat transfer of laminar flow over a plate embedded in porous medium with a constant heat flux under local non-equilibrium condition[J]. CIESC Journal, 2010, 61(1): 10-14.
[17] Ramos M V, Kasai E, Kano J, et al. Numerical simulation model of the iron ore sintering process directly describing the agglomeration phenomenon of granules in the packed bed[J]. ISIJ International, 2000, 40(5): 448-454.
[18] 周萍, 周乃君, 蒋爱华, 等. 传递过程原理及其数值仿真[M]. 长沙: 中南大学出版社, 2006: 300.
ZHOU Ping, ZHOU Naijun, JIANG Aihua, et, al. Principle and numerical simulation of transport processes[M]. Changsha: Central South University Press, 2006: 300.
[19] 鞭岩, 森山昭. 冶金反应工程学[M]. 蔡志鹏, 谢裕生, 译. 北京: 科学出版社, 1981: 282-288.
Muchi I, Moriyama A. Reaction engineering in metallurgical[M]. CAI Zhipeng, XIE Yusheng, trans. Beijing: Science Press, 1981: 282-288.
[20] Tan P, Neuschütz D. Study on polychlorinated dibenzo-p-dioxin/furan formation in iron ore sintering process[J]. Metallurgical and Materials Transactions B, 2004, 35(5): 983-991.
[21] Carvalho M G, Farias T, Fontes P. Predicting radiative heat transfer in absorbing, emitting, and scattering media using the discrete transfer method[C]//Heat Transfer Division, New York: American Society of Mechanical Engineers, 1991, 160, 17-26.
(编辑 邓履翔)
收稿日期:2012-03-10;修回日期:2012-05-25
基金项目:能源高效清洁利用湖南省高校重点实验室基金资助项目(2011NGQ001)
通信作者:张家元(1968-),男,湖北浠水人,博士,教授,从事热能工程教学与研究工作;电话:0731-88876111;E-mail:zjyzhq@csu.edu.cn