J. Cent. South Univ. Technol. (2011) 18: 1733-1737

DOI: 10.1007/s11771-011-0895-z

Function chain neural network prediction on heat transfer performance of oscillating heat pipe based on grey relational analysis

E Jia-qiang(鄂加强)^{1, 2}, LI Yu-qiang(李玉强)^{1, 2}, GONG Jin-ke(龚金科)^{1, 2}

1. State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body, Hunan University, Changsha 410082, China;

2. College of Mechanical and Vehicle Engineering, Hunan University, Changsha 410082, China

? Central South University Press and Springer-Verlag Berlin Heidelberg 2011

Abstract: As for the factors affecting the heat transfer performance of complex and nonlinear oscillating heat pipe (OHP), grey relational analysis (GRA) was used to deal with the relationship between heat transfer rate of a looped copper-water OHP and charging ratio, inner diameter, inclination angel, heat input, number of turns, and the main influencing factors were defined. Then, forecasting model was obtained by using main influencing factors (such as charging ratio, interior diameter, and inclination angel) as the inputs of function chain neural network. The results show that the relative average error between the predicted and actual value is 4%, which illustrates that the function chain neural network can be applied to predict the performance of OHP accurately.

Key words: oscillating heat pipe; grey relational analysis; function chain neural network; heat transfer

1 Introduction

Oscillating heat pipe (OHP) is a new unique heat transfer component and proposed firstly by AKACHI. Heat is transported from evaporator to condenser section by the oscillation of working fluid moving in an axial direction inside the tube.

In recent years, oscillating heat pipe was studied primarily based on experiments and many important factors affecting the characteristics [1] of oscillating heat pipe were identified based on univariant analysis by scholars such as KHANDEKAR et al [2], RITTIDECH et al [3], TONG et al [4], CUI et al [5], and CHAROESAWAN and TERDTOON [6]. The effects of charging ratio, inclination angle and heat input flux based on statistical methods were analyzed in Ref.[7]. There were few reports on the influencing degree of various factors on the heat transfer performance. In this work, grey relational analysis is used to deal with the relationship between the heat transfer rate of a looped copper-water OHP and charging ratio, interior diameter, inclination angel, heat input, number of corners, and to define the main and minor influencing factors instead of traditional mathematical statistics.

In Ref.[8], artificial neural network was used to predict the heat transfer rate without consideration of physical process. Moreover, fewer factors were considered and an ideal neural network model could not be put forward. In this work, the function chain neural network with main affecting factors as inputs is used to predict the heat transfer performance.

2 Experimental

2.1 Experimental system

Figure 1 shows the experimental set-up which consists of a looped copper-water OHP with evaporator section, adiabatic section and condenser section and their lengths are all 50 mm. The evaporator section is heated by hot water, and the inlet temperature is maintained at   80 °C. The heat input is controlled through hot water flow rate measured with a volumetric flowmeter. Heat is removed from the condensation section by 20 °C water from cold bath with constant volumetric flow rate of   30 L/h. Copper constant thermocouples are installed in corresponding water inlet and outlet. And the temperature is displayed and recorded by data acquisition/switch unit (Agilent 34970A).

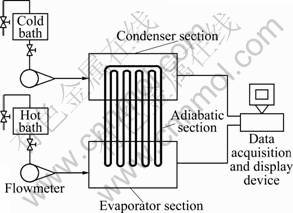
Fig.1 Schematic diagram of equipment apparatus

It is difficult to measure the wall temperature by thermocouple. So, the heat transfer performance could be explained as the heat transfer rate Q_e that is determined by Eq.(1) instead of thermal resistance:

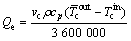                                       (1)

where v_c=30 L/h and T_cⁱⁿ=20 °C. For the fluctuation of the outlet temperature, the average temperature 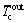 in    2 min is taken as the representative outlet temperature.

2.2 Experimental results

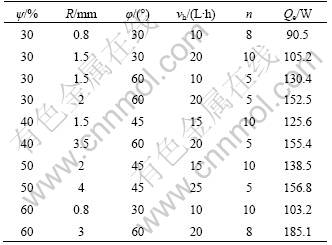
Five factors that affect the heat transfer rate are researched by experiment. They are charging ratio ψ (30% ≤ψ ≤ 60%), interior diameter R (0 mm ≤ R ≤4 mm), inclination angel φ (30° ≤ φ ≤ 60°), the number of turns n (5 ≤ n ≤ 10), and heat input determined by hot water flow rate v_h (10 L/h ≤ v_h ≤ 25 L/h). The results are listed in Table 1.

Table 1 Experimental results of heat transfer performance

3 Grey relational analysis of factors affecting heat transfer performance

3.1 Grey relational generating

When the units in which the performance is measured are different for different attributes, the influence of some attributes may be neglected. This may also happen if some performance attributes have a very large range. In addition, if the goals and directions of these attributes are different, it will cause incorrect results in the analysis. Grey relational generating is a process of transferring the original sequence to a comparable sequence. For this purpose, the experimental results are normalized in the range between zero and one. The normalization can be done by Eq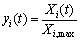.(2):

                                                 (2)

where y_i(t) is the value after the grey relational generating, X_{i, max} is the largest value of X_i(t).

3.2 Grey relational analysis

Following data pre-processing, a grey relational coefficient is calculated to express the relationship between the ideal and actual normalized experimental results. The grey relational coefficient can be expressed as [9-13]

                                        (3)

where Δ_ij is the deviation sequence of the reference sequence X₀(t) and the comparability sequence X_i(t).

,

,

,

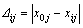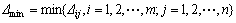ζ is the distinguishing coefficient, ζ∈[0,1]. ζ=0.5 is generally used.

After obtaining the grey relational coefficient, we normally take the average of the grey relation coefficient as the grey relation grade, which is defined by

                                                   (4)

In Eq.(4), γ_k is the grey relation grade between X_i and X₀. It represents the level of relation between the reference sequence and the comparability sequence. The grey relation grade indicates the degree of influence that the comparability sequence could exert over the reference sequence. Therefore, if a particular comparability sequence is more important than the other comparability sequences to the reference sequence, then the grey relational grade for that comparability sequence and reference sequence will be higher than other grey relational grades.

The heat transfer rate is regarded as reference series (X₀) and charging ratio, interior diameter, inclination angel, heat input, numbers of turns are regarded as comparable series (X₁, X₂, X₃, X₄, X₅). Then, the entire results of grey relational generating are shown as

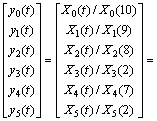
(5)

Equations (6) and (7) show the grey relational coefficient and grade by applying Eqs.(3) and (4):

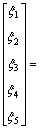
 (6)

As a result, the relational grade is obtained and shown as

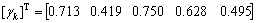         (7)

3.3 Results and analysis

It is clearly observed from Eq.(7) that the grey relation grade of charging ratio ψ is the highest and the grey relation grade of interior diameter R and number of turns n are smaller than the other parameters. With the above results, it is summarized that charging ratio, inclination angel, and heat input are main influencing factors, which have great significance for increasing the heat transfer performance of OHP.

4 Intelligent prediction of heat transfer rate

4.1 Function chain neural network with three inputs

Assuming that fitted output value of heat transfer rate can be described by n-order polynomial function (three-order is enough to describe the nonlinear function):

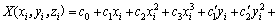
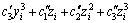                                   (8)

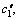
where x_i is the charging ratio, y_i is the inclination angel, z_i is the hot water flow rate and X(x_i, y_i, z_i) is the heat transfer rate, and c₀, c₁, c₂, c₃,     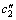 and 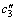 are fitted coefficients.

The function joint is shown in Fig.2. Many additional functions are incentive when a node (such as node k) is actuated in a conceptual network model based on mathematics and parallel distributed processing. Then, x_i and g₀(x_k), g₁(x_k), …, g_n(x_k) will be gotten accordingly. In principle, it is possible to realize the supervised learning of the monolayer neural network when using function link.

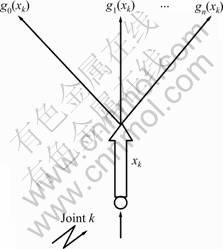
Fig.2 Schematic diagram of function joint

The function link neural network [14-15] with three inputs is shown in Fig.3. Assuming that neurons are linear, the inputs of neural network are 1, x_i, x_i², x_i³, y_i, y_i², y_i³, z_i, z_i², z_i³. The output of function link can be found by the following expression:

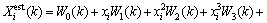
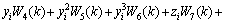
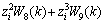                                             (9)

In Eq.(9), W_j(k) is the weight at the k-th step, and W_j(k+1)=W_j(k)+η_ie_j(k), 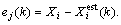 η_i is the learning factor which can affect the iteration times. X_i   is the actual heat power value corresponding to the i-th charging ratio, inclination angel, and hot water flow rate.

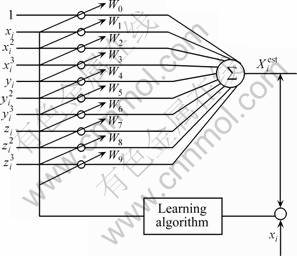
Fig.3 Schematic diagram of there-input function link neural network

The minimum mean square error of the actual heat transfer rate within the global scope can be obtained after the error between the output and actual value is learned in function chain neural network:

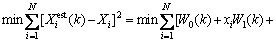
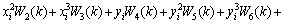
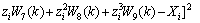                 (10)

The minimum mean square is the function of weight (W₀-W₉).

Figure 4 shows that the simulation results fit well with the actual values, which illustrates the function chain neural network can achieve its nonlinear relationship preferably .

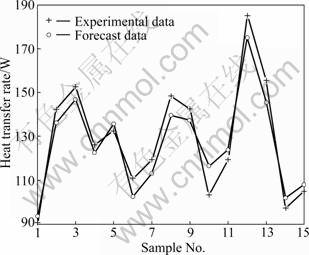
Fig.4 Fitting results of three-input function chain neural network

From Table 2, we can see that the actual and predicted results are very near and their relative average error is 4%. This indicates that the function chain neural network in which the charging ratio, inclination angel, and heat input are used as inputs has enough accuracy.

4.2 Function chain neural network with four inputs

The function chain neural network of heat transfer rate with four inputs can be described by the three-order polynomial function as

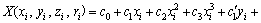
(11)

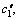
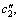
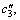
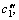
where r_i is the number of turns, other variables are the same as the above, and c₀, c₁, c₂, c₃,        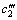 and  are fitted coefficients.

The function chain neural network with four inputs is shown in Fig.5. The input values of neural network are 1, x_i, x_i², x_i³, y_i, y_i², y_i³, z_i, z_i², z_i³, r_i, r_i², r_i³. The output value of functional chain can be found by the following expression:

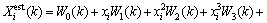
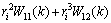                                  (12)

Table 2 Comparison of actual and predicted results

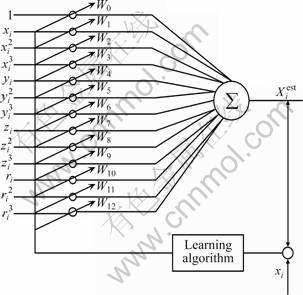
Fig.5 Schematic diagram of four-input function chain neural network

Similar to the above results, we can see that the actual and predicted results are very near in the function chain neural network in which the charging ratio, inclination angel, heat input, and the number of turns are taken as inputs from Fig.6, but their relative average error increases from 4% to 5%. The fitting degree has no improvement, but the complexity of neural network structure is rather increased, which can cause longer learning time, slow down the convergence speed and reduce the prediction accuracy.

Fig.6 Fitting results of four-input function chain neural network

It can be concluded that the variables whose relational grade is more than 0.5 should be selected only as the inputs in establishing the multi-input function chain neural network, which can not only ensure the function chain neural network fitting precision, but also reduce the unnecessary computation time.

5 Conclusions

1) It is of great significance for improving the heat transfer performance by using the grey relational analysis to deal with the relationship between the heat transfer rate of a looped copper-water OHP and charging ratio, interior diameter, inclination angel, heat input, number of turns, and to define the main and minor impacting factors.

2) In order to guarantee the fitting precision and save the computing time, input variables should be only variables whose relational grade is more than 0.5 in establishing the multi-input function chain neural network.

3) The relative average error between predicted and actual value is 4% in function chain neural network, with charging ratio, inclination angel, heat input as inputs and the heat transfer rate as output, which illustrates that this model can predict the heat transfer performance of OHP well.

References

[1] GROLL M, KHANDEKAR S. Pulsating heat pipes: A challenge and still unsolved problem in heat pipe science [J]. Archives of Thermodynamics, 2002, 23(4): 17-28.

[2] KHANDERKAR S, DOLLINGER N, GROLL M. Understanding operational regimes of pulsating heat pipes: An experimental study [J]. Applied Thermal Engineering, 2003, 23(6): 707-719.

[3] RITTIDECH S, TERDTOON P, MURAKAMI M, KAMONPET P, JOMPAKDEE W. Correlation to predict heat transfer characteristics of a closed-end oscillating heat pipe at normal operating condition [J]. Applied Thermal Engineering, 2003, 23(4): 497-510.

[4] TONG B Y, WONG T N, OOI K T. Closed-loop pulsating heat pipe [J]. Applied Thermal Engineering, 2001, 21(18): 1845-1862.

[5] CUI Xiao-yu, WENG Jian-hua, GROLL M. Experimental investigation of heat transfer performance for the cooper/water pulsating heat pipe [J]. Journal of Engineering Thermo physics, 2003, 24(5): 864-86.

[6] CHAROENSAWAN P, TERDTOON P. Thermal performance of horizontal closed-loop oscillating heat pipes [J]. Applied Thermal Engineering, 2003, 28(5): 460-466.

[7] MA Yong-xi, ZHANG Hong. Analysis of heat transfer performance of oscillating heat pipes based on a central composite design [J]. Chinese Journal of Chinese Engineering, 2006, 14(2): 223-228.

[8] CUI Xiao-yu, WENG Jian-hua, GROLL M. Heat transfer performance model of pulsating heat pipe based on neural network [J]. Journal of Chemical Industry and Engineering, 2003, 54(9): 1319-1322. (in Chinese)­­­­­­­

[9] CAYDAS U, HASCALIK A. Use of the grey relational analysis to determine optimum laser cutting parameters with multi-performance characteristics [J]. Optics & Laser Technology, 2008, 40(7): 987-994.

[10] LIN J L, LIN C L. The use of the orthogonal array with grey relational analysis to optimize the electrical discharge machining process with multiple performance characteristics [J]. International Journal of Machine Tools and Manufacture, 2002, 42(2): 237-244.

[11] TSENG M L. Using linguistic preferences and grey relational analysis to optimize the thin-film sputtering process with multiple quality characteristic in color filter manufacturing [J]. Expert System with Applications, 2010, 37(1): 70-81.

[12] RAO R, YADAVA V. Multi-objective optimization of Nd:YAG laser cutting of thin superalloy sheet using grey relational analysis with entropy measurement[J]. Optics & Laser Technology, 2009, 41(8): 922-930.

[13] FU Chao-yang, ZHENG Jia-shen, ZHAO Jing-mao, XU Wei-dong. Application of grey relational analysis for corrosion failure of oil tubes[J]. Corrosion Science, 2001, 43(5): 881-889.

[14] E Jia-qiang, ZHANG Hua-mei, GONG Jin-ke, WANG Yao-nan. Measurement system for gas flux in pipeline based on function chain neural network [J]. Journal of Central South University: Science and Technology, 2006, 39(5): 976-979. (in Chinese)­­­­­­­

[15] LIU Meng-xiang, ZHONG Zhi-hua, GONG Jin-ke. Data acquisition system of cylinder pressure in vehicle engine based on function chain neural network [J]. Journal of Hunan University: Natural Sciences, 2007, 34(4): 29-33. (in Chinese)­­­­­­­

(Edited by YANG Bing)

Foundation item: Project(531107040300) supported by the Fundamental Research Funds for the Central Universities in China; Project(2006BAJ04B04) supported by the National Science and Technology Pillar Program during the Eleventh Five-year Plan Period of China

Received date: 2010-09-03; Accepted date: 2010-12-24

Corresponding author: LI Yu-qiang, PhD Candidate; Tel: +86-13787248343; E-mail: lucky_qiang860214@yahoo.com.cn