J. Cent. South Univ. (2017) 24: 1671-1675
DOI: 10.1007/s11771-017-3573-y
Initial densification strain point’s determination of honeycomb structure subjected to out-of-plane compression
WANG Zhong-gang(王中钢)1, 2, ZHOU Wei(周伟)1, LIU Jie-fu(刘杰夫)1
1. School of Traffic & Transportation Engineering, Key laboratory of Traffic Safety on Track of
Ministry of Education, Central South University, Changsha 410075, China;
2. CRRC Qingdao Sifang Co. Ltd., Qingdao 266111, China
 Central South University Press and Springer-Verlag Berlin Heidelberg 2017
Central South University Press and Springer-Verlag Berlin Heidelberg 2017
Abstract: Compression ratio is significant for cellular structures on energy absorption. In the present work, theoretical formulas to determine the initial densification strain of honeycomb structure were put forward by means of minimum energy principle. Detailed densification strain points were identified, with full fold model for kinds of specimens. To validate, corresponding numerical simulations were carried out with explicit finite element method. Excellent agreement in terms of initial densification stain point has been observed between the theoretical calculation and numerical simulation. The results show that: ① different honeycomb structure has different initial densification strain point, and its geometric configuration of cells plays an evident role on densification; ② half-wave length of the wrinkle of honeycomb in folding process significantly influences on the densification strain point; ③ the initial densification point is an decreasing power function of the ratio of foil thickness to cell length, with the exponent 2/3. These achievements provide important references for design in cellular energy absorption devices.
Key words: honeycomb; densification strain; full fold element; half-wave length
1 Introduction
Train collision accident caused heavy casualties, huge economic losses and serious social impact, which has become a hot and advanced issue. Exploiting train’s crashworthiness and special energy absorption devices are effective methods to reduce the danger even avoid this fatal catastrophe [1]. For this purpose, scientists devote themselves to develop high effective energy absorption device to dissipate the huge impact kinetic in crash in the past several years [2-5].
Cellular honeycomb structure, due to its light, excellent specific energy absorption, stable mechanical performance, has been considered as the main potential energy absorbing material in engineering application circle [6]. The critical properties to energy absorption are plateau stress and densification strain, not only in the aluminum and paper honeycomb core [7], but also in other cellular structures. On the topic of the plateau stress, abundant research works have been conducted, and plenteous achievements have been obtained [8-10]. However, only a little literature is specialized in the topic of densification strain so far. A formula to express the ultimate densification strain for foam was firstly presented in Ref. [11] by multiplying an experimental scale before the relative density. Another preliminary evaluation of compressive final densification strain of paper honeycomb with the principle of mass conservation was introduced in Ref.[12].
As it was well known, at densification stage, the stress of honeycomb increases rapidly with tiny strain, where the honeycomb almost lost its energy absorption ability. The initial densification strain point is a key index to assess the energy absorption capacity for any given piece of honeycomb block. Hence, in earlier study, the compression ratio was designated as an approximate value based on experience or experiment [13]. Up to now, it is still lack of scientific formulas to theoretically describe the initial densification strain of honeycomb structure. The problem results either in lacking of sufficient redundancy or in wasting energy absorption capacity. Determining the initial densification strain point for cellular structure is urgent.
Differing from the conventional experience or limited time of experiment, in this investigation, theoretical formulas and numerical simulation with explicit finite element methodology were attempted. These achievements provide important reference for design in energy absorption devices, particularly for special energy absorber of bullet train.
2 Theoretical calculations
2.1 Initial densification point
For any piece of honeycomb block, it consists of lots of Y-shape units as basic element (see Fig. 1). In each Y unit, it can be described by the foil thickness of cell wall t, cell length h, cell width l, and tilt angle θ. This work only discusses the case of θ=π/6.
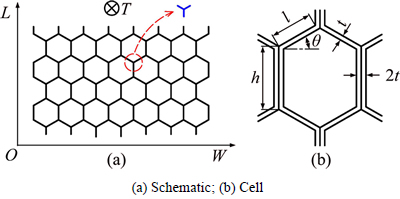
Fig. 1 Honeycomb structure
When subjected to axial compression at T-direction, the honeycomb goes through the elastic, plastic progressive collapse and densification stage, as shown in Fig. 2(a), where D-E is the densification stage. At the transition region from plateau to densification, the turning corner is the initial densification strain point (see Fig.2 (a)). Once stepping over it, the stress increases rapidly with the compression strain.
In the compression process, the foil is folding periodically, one by one, until all foil collapsed. Such process can be elucidated by the schematic of folds see Fig. 2(b), in which H stands for the half-wave length. Obviously, once H is identified, the initial densification strain point can be obtained.
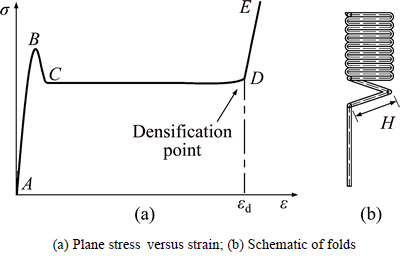
Fig. 2 Progress history of honeycomb structure
2.2 Theoretical formulas
To obtained H, the plastic energy dissipated by cell foils should be calculated. For each Y unit, according to classic Wierzbicki model [14], the deformation energy mainly includes three forms including the plastic extension energy E1 dissipated during the stretching of the toroidal shell, the plastic energy E2 consumed by horizontal plastic hinge lines in the forming of the cylindrical surfaces, and the energy E3 dissipated by inclined plastic hinge lines in the forming of conical sections, respectively as [13]
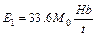 (1a)
(1a)
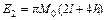 (1b)
(1b)
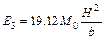 (1c)
(1c)
where temporary parameter b is the small radius of the toroidal shell and M0 is the fully plastic bending moment calculated as M0=σ0t2/4 (σ0 is the static yield stress of foil material). Hence, the total energy EY can be summed by these three parts of energy as
 (2)
(2)
According to the energy balance principle, at 2H folding distance, for each Y unit, EY will be exhausted under the external compression. That means
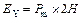 (3)
(3)
where Pm means the mean crushing force. Combining Eq. (2) with Eq. (3), Pm can be expressed as
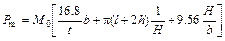 (4)
(4)
The minimal energy principle tells that the least Pm leads to collapse happen. Hence, H and b can be determined by letting 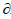 Pm/
Pm/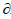 H=0 and
H=0 and 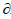 Pm/
Pm/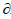 b=0. Consequently, H can be obtained as
b=0. Consequently, H can be obtained as
 (5)
(5)
Now, assuming the height at T-direction of honeycomb core is Q (see Fig. 1(a)), the total number of folding cycles n along the compressed T-direction can be calculated as
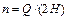 (6)
(6)
Between each fold, there are four layers of foil in each Y unit. For the commercial product, the plastic buckling mode is almost dominated by foils in interaction area because of their double thickness here. At the same time, there is an interlaced fold between each neighboring corrugation. Thus, for each foil, the total residual thickness S of unfolding part is
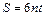 (7)
(7)
Hence, the densification strain εd can be calculated as
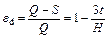 (8)
(8)
Combining Eq. (8) with Eqs. (6) and (7), the densification strain can be rewritten as
 (9)
(9)
Now, the initial densification strain point has been identified theoretically.
3 Numerical simulation
3.1 Finite element model
In recent years, explicit finite element methodology has been widely used in analysis of cellular honeycomb structures [15-18], due to its economic efficiency. Among the mainstream of the commercial software, LS-DYNA [19] is a mature and efficient simulation software package. In this work, the finite element model of each specimen was built with LS-DYNA
[19] is a mature and efficient simulation software package. In this work, the finite element model of each specimen was built with LS-DYNA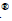 . Each model has 13 cells at L-direction and 11 cells at W-direction (see Fig. 1(a)), which completely satisfying the requirement of minimum cells (see Refs. [10, 13]). They were all of 40 mm at T-direction. All the numerical simulations have been conducted based on a properly defined discretization, using a mesh size of 0.5 mm for the whole honeycomb specimen.
. Each model has 13 cells at L-direction and 11 cells at W-direction (see Fig. 1(a)), which completely satisfying the requirement of minimum cells (see Refs. [10, 13]). They were all of 40 mm at T-direction. All the numerical simulations have been conducted based on a properly defined discretization, using a mesh size of 0.5 mm for the whole honeycomb specimen.
The mechanical properties of foil material were as follows, density 2680 kg/m3, elastic module 69.3 GPa, Poisson ratio 0.33, yield stress 215 MPa. In this investigation, the foil material was treated as an ideal elastic-plastic constitutive model. Automatic single surface contact algorithm was applied to avoid penetration between cell walls. The specimen was placed on a static rigid plate as a boundary and crushed by another moving rigid plate at a constant velocity.
3.2 Results
Before comprehensive analyses, strain rate effect on the initial densification strain point should be identified, since the former derivation is obtained based on quasi-static situation. Figure 3 shows the representative results of these specimens (t=0.06 mm, h=4 mm, l=4 mm) subjected to axial impact at a constant velocity of 1 m/s, 5 m/s, 10 m/s, 50 m/s, respectively.
From Fig. 3, it can be clearly seen that when undergoing different axial loadings, densification strain nearly keeps around 0.783 for cases at 1 m/s, 5 m/s,10 m/s. Meanwhile, for case at 50 m/s, evident wave can be observed clearly. That means the densification strain is insensitive, almost maintains the same value, no matter at quasi-static or dynamic loading situation. Hence, in all of the subsequent simulations, the impact velocity was designed as 10 m/s.
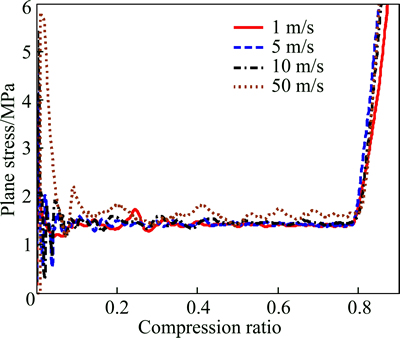
Fig. 3 Curves of plane stress against compression ratio at different velocities
For the convenience of expression, λ was defined as λ=l/h here. It denoted the ratio of cell length to cell width. Figure 4 streamed resultant plane stress curves versus compression ratio of seven different situations as λ=0.75, λ=1.00, λ=1.25, λ=1.50, λ=1.75, λ=2.00. In these cases, they all met h=4 mm.
Fig. 4 Curves of plane stress versus compression ratio of different specimens
From Fig. 4, it can be found that different honeycombs with different geometric configurations have different initial densification strain points, yet they perform the same response history. Table 1 reports the initial densification strain points obtained theoretically as well as numerically. Defining relative error Δ, and it is calculated as
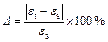 (10)
(10)
where εt is the theoretical result; εs is the strain of numerical simulation. Corresponding relative errors have been listed in Table 1.
Table 1 Comparison of different initial densification strain (t=0.06 mm, h=4 mm)
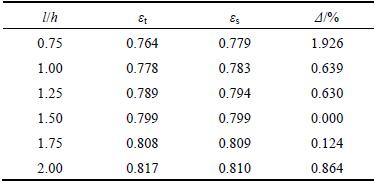
From the comparison between the data given in Table 1, it can be found that, the maximum error among all of them is merely 1.926%, and the average error is merely 0.697%. Good agreement between the theoretical results and numerical simulation were observed. The theoretical formula has been validated to be a reliable way to calculate precise initial densification strain points of honeycomb structures. Considering the simulation results in Table 1, a fitting function used to describe the relationship between initial densification strain point and geometric configuration (in case of h=l) can be constructed as below.
 (11)
(11)
where εdf means the fitting result. It has approximate coefficient with that in Eq. (9).
4 Discussions
For hexagonal honeycomb, l=h, hence, Eq. (9) can be simplified as
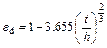 (12)
(12)
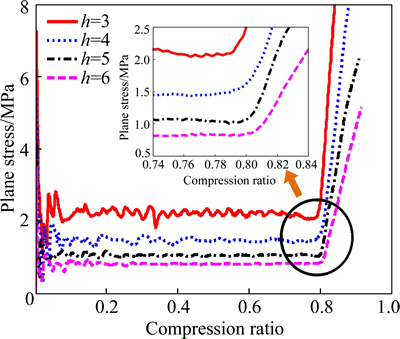
Fig. 5 Curves of plane stress versus compression ratio of different hexagonal specimens
For further comparison, four kinds of hexagonal honeycomb specimens (h=l), with h=3 mm, h=4 mm, h=5 mm, h=6 mm were employed here, respectively. Figure 5 streams corresponding resultant response curves of plane stress versus compression ratio below. Typical trend of plane stress-strain curve can also be found in hexagonal honeycomb.
Table 2 reports corresponding results with different length of hexagonal cells, and relative errors were calculated according to Eq. (10). Figure 6 streams the numerical, fitting and theoretical results below. Outstanding coincidence between the theoretical results and simulation can be observed.
Table 2 Comparison between theoretical results, fitting results and simulation for initial densification strain (t =0.06 mm)
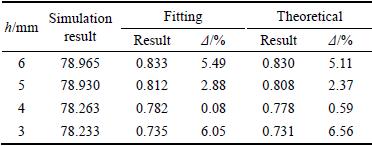
From Table 2, Figs. 5 and 6, it can be seen that with the decreasing of cell length from 6 mm to 3 mm, the initial densification strain decreases from 78.965 to 78.233 in numerical simulation. The maximum error appears in case of h=3 mm, which is 6.56%, evidently larger than that in case of h=4 mm. It is a very good result for engineering application. The reason for this mainly lies in the localized collapse happens close to densification, where an unloading phenomenon can be seen (see Fig. 5).
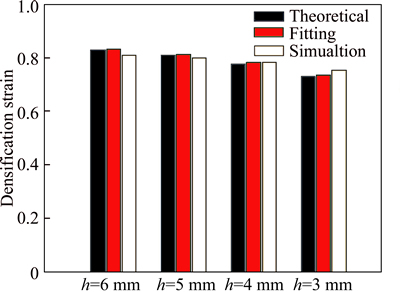
Fig. 6 Comparison of densification strain point between kinds of results
Furthermore, compared with the same power function of t/h in theoretical model used to express the lock densification [12], the difference lies in the exponent, 1 for Ref. [12], 2/3 for the present work. In addition, of the densification strain ratio, MAHMOUDABADI and SADIGHI also indirectly provided a scope from 0.74-0.82. Compared with the results of Refs. [12, 20], a more precise result can be obtained by this work.
To directly exhibit the appearance of initial densification strain point, Fig. 7 shows representative transition process as below for typical Y unit in case of h=4 mm. As seen in Fig. 7 that the honeycomb goes through three typical stages, including: ① former densification stage, ② critical densification progress, and ③ lock strain stage. At the critical densification stage, the foil is still stretched (see dashed frame). With the deepening of compression, the foil folds, local band shapes, further densification and compaction follow.
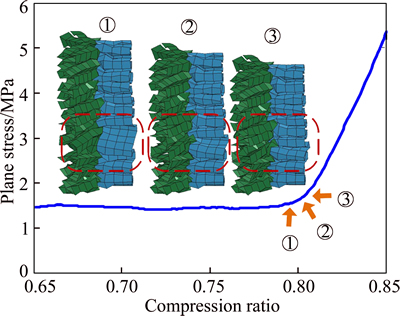
Fig. 7 Representative densification process (h=4 mm)
5 Conclusions
1) Half-wave length has significant influence on the densification strain point of the honeycomb structure. Once it was identified, the densification strain point can be determined. The diversity of geometric configuration of honeycomb leads to different half-wave length. So, the topology of unit cell has a direct effect on the densification strain point.
2) The impact velocity is insensitive to the densification. For honeycomb structure, the initial densification strain point is closely related to the ratio of foil thickness versus cell length (t/h), performing a power function of t/h, with the exponent 2/3.
3) For honeycomb structure, before lock strain stage, it goes through a transition region, where periodical fold shapes completely, and the initial densification point arrivals.
References
[1] WANG W B, REN L H, ZHOU H C, HECHT M. Energy absorption configuration of crashworthy metro train [J]. Advanced Materials Research, 2012, 466-467: 724-728.
[2] DONG Hai-peng, GAO Guang-jun, XIE Su-chao, LI Jian. Collision performance of bitubular tubes with diaphragms [J]. Journal of Central South University, 2015, 22(9):3657-3665.
[3] GAO G, DONG H, TIAN H. Collision performance of square tubes with diaphragms [J]. Thin-Walled Structures, 2014, 80(1): 167-177.
[4] ASHBY M F, JOHNSON K. Materials and design, third edition: The art and science of material selection in product design [M]. Waltham: Butterworth-Heinemann, 2014.
[5] WANG Z G, GAO G J, TIAN H Q, LU Z J. A stability maintenance method and experiments for multi-player tandem aluminum honeycomb array [J]. International Journal of Crashworthiness, 2013, 18(5): 483-491.
[6] LI Meng, DENG Zhong-quan GUO Hong-wei, LIU Rong-qiang, DING Bei-chen. Optimizing crashworthiness design of square honeycomb structure [J]. Journal of Central South University, 2014, 21(3): 912-919.
[7] BAI Z, WANG D, XU Z. Model creation of strain rate-dependent energy absorption for paper honeycomb sandwich structure [J]. Journal of Sandwich Structures & Materials, 2015, 17(4): 359-375.
[8] AKTAY L, JOHNSON A F, KROPLIN B H. Numerical modeling of honeycomb core crush behavior [J]. Engineering Fracture Mechanics, 2008, 75(9): 2616-2630.
[9] WANG Zhong-gang, LU Zhai-jun. Experimental assessment on energy absorption property of aluminum honeycomb under out-of- plane compression [J]. Journal of Central South University: Science and Technology, 2013, 44(3): 1246-1251. (in Chinese)
[10] WANG Z G, TIAN H Q, LU Z J, ZHOU W. High-speed axial impact of aluminum honeycomb—Experiments and simulations [J]. Composites Part B, 2014, 56(1): 1-8.
[11] GIBSON L J, ASHBY M F. Cellular solids, structures and properties [M]. 2nd ed. Cambridge: Cambridge University Press, 1997.
[12] WANG Dong-mei WANG Zhi-wei. Evaluation of compressive densification strain of paper honeycombs [J]. Journal of Mechanical Engineering, 2009, 45(5): 285-289.
[13] WANG Z G, LU Z J, TIAN H Q, YAO Song, ZHOU W. Theoretical assessment methodology on axial compressed hexagonal honeycomb’s energy absorption capability [J]. Mechanics of Advanced Materials & Structures, 2016, 23(6): 503-512.
[14] LU G X, YU T X. Energy absorption of structures and materials [M]. Cambridge: Woodhead Publishing, 2001.
[15] WANG Z, LU Z, YAO S, DAVID H, LUCIANO F. Deformation mode evolutional mechanism of honeycomb structure when undergoing a shallow inclined load [J]. Composite Structure. 2016, 147: 211-219.
[16] WANG Z, YAO S, LU Z. Matching effect of honeycomb-filled thin-walled square tube—experiment and simulation [J]. Composite Structure, 2016, 157: 494-505.
[17] WANG Z, LIU J, DAVID H. Mechanical behaviors of inclined cell honeycomb structure subjected to compression [J]. Composites Part B, 2017, 110: 307-314.
[18] WANG Z, LIU J, LU Z, DAVID H. Mechanical behavior of composited structure filled with tandem honeycombs [J]. Composites Part B, 2017, 114: 128-138. DOI. 10.1016/j.compositesb. 2017.01. 018.
[19] HALLQUIST J. LS-DYNA user’s manual, 970ed [R]. Troy: Livemore Software Technology Corporation, 2003.
[20] MAHMOUDABADI M Z, SADIGHI M. A theoretical and experimental study on metal hexagonal honeycomb crushing under quasi-static and low velocity impact loading [J]. Materials Science & Engineering A, 2011, 528(15): 4958-4966.
(Edited by DENG Lü-xiang)
Cite this article as: WANG Zhong-gang, ZHOU Wei, LIU Jie-fu. Initial densification strain point’s determination of honeycomb structure subjected to out-of-plane compression [J]. Journal of Central South University, 2017, 24(7): 1671-1675. DOI: 10.1007/s11771-017-3573-y.
Foundation item: Project(51505502) supported by the National Natural Science Foundation of China; Project(2015BAG13B01) supported by the National Key Technology Support Program, China; Project(ZZYJKT2017-09) supported by the State Key Laboratory of High Performance Complex Manufacturing, China; Project supported by the Open End Fund for the Valuable and Precision Instrument of Central Sonth University, China
Received date: 2016-02-09; Accepted date: 2017-01-11
Corresponding author: WANG Zhong-gang, PhD; Tel: +86-731-82655294; E-mail: wangzg@csu.edu.cn