Trans. Nonferrous Met. Soc. China 28(2018) 220-225

Correlating oriented grain number density of recrystallisation in particle-containing aluminium alloys

Qing-long ZHAO¹, Hui-di ZHANG¹, Ke HUANG², Knut MARTHINSEN³

1. Key Laboratory of Automobile Materials, Ministry of Education, College of Materials Science and Engineering, Jilin University, Changchun 130025, China;

2. Laboratory of Thermomechanical Metallurgy - PX Group Chair, Ecole Polytechnique Federale de Lausanne, Neuchatel CH-2002, Switzerland;

3. Department of Materials Science and Engineering, Norwegian University of Science and Technology, Trondheim 7491, Norway

Received 19 October 2016; accepted 3 March 2017

Abstract: The recrystallized grain structure of Al-(Mn)-Fe-Si alloys after isothermal annealing was studied by electron backscatter diffraction (EBSD) technique. Statistical correlation suggests that the frequency of forming P-oriented ({011}<566>) grains at a particle larger than the critical diameter (about 1.1 μm) is about 2% when the effect of fine dispersoids and concurrent precipitation is negligible. The overall grain number density is correlated linearly with the number densities of P and Cube ({001}<100>) grains. The grain number densities of typical orientations (P, ND-rotated cube {001}<310> and Cube) and the overall recrystallized grains increase as rolling strain increases, following a similar exponential law.

Key words: recrystallisation texture; aluminium alloys; particle-stimulated nucleation; EBSD

1 Introduction

Aluminium is the metallic material of choice for light-weight applications. Industrial aluminium alloys usually contain second-phase particles which are formed during casting and heat treatments and induce inhomogeneity of deformation in the matrix. For instance, deformation zones are formed around large particles, which may act as nucleation sites of recrystallisation due to high stored energy during back annealing of deformed samples [1]. This mechanism is known as particle simulated nucleation (PSN) [2]. By contrast, fine particles affect deformation [3], induce Zener drag effect on boundary migration and retard recrystallisation [4,5]. Thus, particle size and their distribution affect recrystallization structure and texture. Different recrystallisation texture components are formed by various mechanisms [6]. For instance, it is widely accepted that Cube component {001}<100> is formed at cube (transition) bands by strain induced boundary migration (SIBM) [2,7]. P component is commonly observed in Al-Mn alloys with considerable precipitation [8-11]. Low heating rates promote P texture, when precipitation of dispersoids occurs prior to or concurrently with recrystallization [12]. Recently, P-oriented grains are found in commercially pure aluminium as well [13,14], and P component is usually very weak due to its low number fraction and grain size [14]. Simulations and experimental characterization suggest that P-oriented grains originate within deformation zones and are promoted by increasing rolling strain [12,15].

The activity of various recrystallisation mechanisms is influenced by microchemistry, deformation strains, and annealing treatments etc [2,4,6,16]. Modelling of recrystallisation texture is an important aspect of alloy and process optimizing in industry, and many efforts have been made to simulate recrystallisation texture [17-20]. However, we still lack a simple relationship to estimate the recrystallisation activity of different texture components, especially the contribution of PSN [17]. The present work aims to identify the correlation of some important recrystallisation texture components with coarse particle distribution and rolling strain in aluminium alloys, and to document the possibility of forming P-oriented grains at a particle, providing a practical relation to estimate the activity of PSN from the particle size distribution.

2 Experimental

Three aluminium model alloys were provided by Hydro aluminium, labelled as B2, C1 and C2. Their chemical compositions are given in Table 1. The raw materials were direct chill (DC) cast billets with a diameter of about 23 cm. Homogenization was performed in an air-circulation furnace with a heating rate of 50 °C/h. C1 was given two different treatments besides the as-cast condition. The homogenization treatments for each sample alloys are listed in Table 1, followed by water quenching. The long-time homogenization of B2 is designed to achieve an equilibrium level of solutes in solid solution. Following different homogenization treatments, all the samples were cold-rolled to 1.5 mm to achieve a thickness reduction of 95%, corresponding to a strain of ε=3. C1-0 slabs of varied thicknesses (30, 7.5 and 3 mm) were cut from the cast billet, and were rolled to final thickness of 1.5 mm, achieving the reductions of 95%, 80% and 50%, respectively. Flash annealing of the rolled sheets was performed in a pre-heated salt bath at 300-500 °C (heating rate in the order of 10² °C/s). The annealing time was selected to be long enough to finish recrystallisation and to avoid further grain growth, according to the softening curves measured by hardness tests (referred to Refs. [14,21]). Electrical conductivity, used as an indication of solid solute content and amount of precipitation, was measured by using a Foerster Sigmatest 2.069 at room temperature. The microstructure was characterized by using backscatter electron imaging in a Zeiss Ultra 55 field emission scanning electron microscope with an EBSD detector. The orientation analysis of recrystallised samples was performed using EDAX’s OIM^TM software.

3 Results and discussion

3.1 Microstructure prior to back annealing

The constituent particles and dispersoids in the experimental materials have been characterised in Refs. [14,21] and a brief introduction is presented here. During homogenization, a relatively high density of fine dispersoids (54 nm in diameter, number density of about 1.3×10⁶ mm^-2) was formed in C1-2. The density of dispersoids was lower (about 5.5×10⁴ mm^-2, 127 nm in diameter) in C1-3, and the lowest (about 1.2×10⁴ mm^-2, 150 nm in diameter) in C2. The diameter and number density of constituent particles after homogenization were measured from SEM observations. The cumulative distribution of constituent particles with diameter larger than d, N(d), can be described by the following  equation [17]:

N(d)=A·exp(-k·d)                             (1)

where A and k are constants which are estimated by fitting the experimental measurements to Eq. (1). The fitting values are listed in Table 1. The morphology of constituent particles is complex, particularly the Si-containing particles, which could be rounded or branched, as demonstrated in Ref. [22]. Branched constituent particles are particularly prone to break during rolling. Figure 1 exemplifies by sample B2 that cold rolling did not evidently change the size distribution of constituent particles, although the number density of very large particles was reduced. The morphology and distribution of constituent particles after rolling for different conditions are demonstrated in Fig. 2. Clusters of particles are observed in C1-0, which are observed in C1-2 and C1-3 as well. The shape of the constituent particles in C2 is more rounded due to coarsening during homogenization at high temperature. A typical β-fibre rolling texture was formed after cold rolling to reduction of 95%.

Table 1 Nominal chemical composition, homogenization treatments, electrical conductivity, constants A and k in Eq. (1) of samples

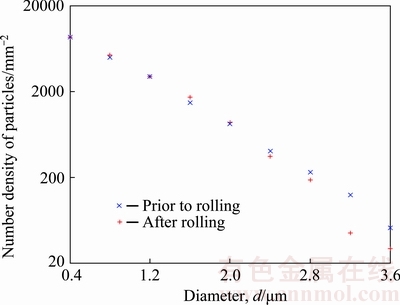
Fig. 1 Cumulative distribution of constituent particles in sample B2 before and after rolling

3.2 Grain number densities of various orientations in recrystallised samples

After homogenization, the samples have different solute levels in solid solution, as indicated by the measured electrical conductivity (Table 1). A low value of electrical conductivity indicates that a high level of solutes was retained in solid solution, e.g. in C1-0 and C2. It led to precipitation which would affect recrystallisation at low temperatures, and then coarse grain structure and strong texture (P and ND-rotated  cube) were formed [14]. Annealed at high temperatures, recrystallisation occurs prior to precipitation, and recrystallisation is not affected by precipitates [14].  Thus, the C1-0 and C2 samples are sensitive to annealing temperature due to their considerable supersaturation, and high annealing temperatures (400 and 450 °C for C2, and 500 °C for C1-0) were selected to limit the influence of precipitation. C1-3 and B2 are insensitive because of low solute contents, and being annealed at 300, 400 and 500 °C. C1-2 was annealed at 400 and 500 °C. An example of recrystallisation texture of C2 is demonstrated in Fig. 3, showing evident Cube and R components.

Fig. 2 Distributions of constituent particles in 95% rolled samples

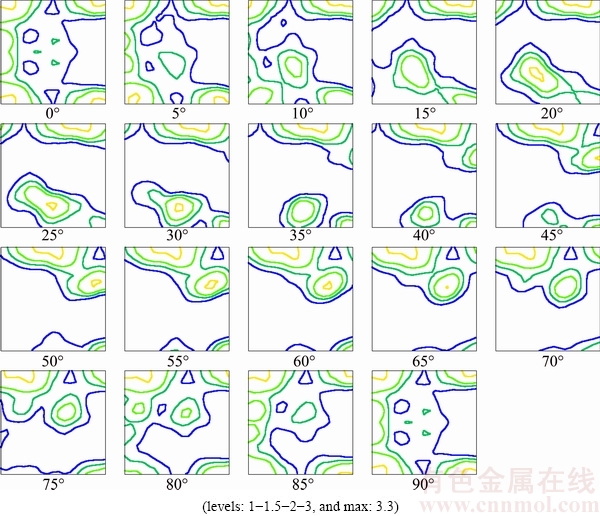
Fig. 3 Recrystallisation textures of sample C2 annealed at 773 K for 5 s

In the present work, we try to identify an empirical relationship between special grain orientations and constituent particles. The grain number densities of P, ND-rotated Cube (NDcube) and Cube orientations in C1-2 and C1-3 are characterised in the present work, while those in C1-0, C2 and B2 have been reported in Ref. [14]. The definitions of the Euler angles are (59.5, 45, 0) for P, (20, 0, 0) for NDcube and (0, 0, 0) for Cube. The deviation angle is defined as 10°. The orientation analysis is based on EBSD scans covering thousands of grains. Particle stimulated nucleation (PSN) is generally accepted as a main nucleation mechanism for aluminium containing large particles. The critical radius of nuclei to grow outside deformation zones can be related to the particle diameter [1]. Then, the density of PSN sites is given by [17]

N_PSN=C_PSN·N(d_c)                              (2)

where C_PSN is a constant determining the average number of nuclei formed at each particle larger than the critical diameter d_c.

The P orientation is a typical component related to PSN. Likewise, the density of nucleation sites for P orientation becomes

N_P=C_P·N(d_c)                                (3)

where C_P is a constant indicating the frequency of P-oriented grains nucleating at particles larger than the critical diameter d_c.

Fitting Eq. (3) correlates the grain number density and the particle size distribution. The best fitting is plotted in Fig. 4. The fitted values of d_c and C_P are 1.1 μm and 0.02, respectively. It is reported that the critical diameter for PSN is above 1 μm [1], which is similar to the fitted value in the present work.  and GOTTSTEIN [12] characterized orientation distribution in deformation zones by EBSD, and  reported that the possibility of finding P orientation in deformation zones was 39% after cold rolling of 70%, and the possibility should be higher as the rolling reduction increases. However, only a small fraction of P-oriented subgrains which are larger than the critical diameter can grow as nuclei of recrystallisation. The small value of C_P suggests that the possibility of forming a P-oriented grain at a constituent particle is very small, only about 2%. Clusters of particles are more efficient as nucleation sites than isolated particles, particularly for small particles, and the morphology of particles may matter as well. However, so far, there is no proper method to quantitatively describe the effects of clustering and morphology. Thus, the estimation in the present work gives a statistical view of PSN, and should be useful for modelling recrystallisation.

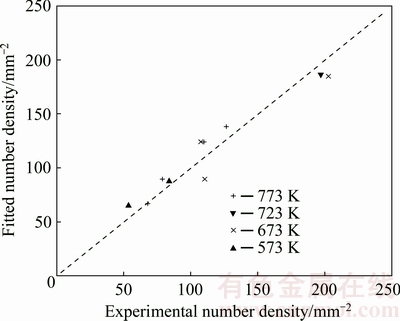
Fig. 4 Correlating number density of P-oriented grains to size distribution of constituent particles according to Eq. (3)

NDcube component is evident together with P texture in alloys annealed at low temperatures when concurrent precipitation occurs. NDcube is usually also considered to be related to large particles [9]. However, the location of NDcube in ODF is very close to Cube. It is possible that a fraction of NDcube nuclei is formed similarly to Cube grains. Here, we try to correlate the grain number density of NDcube to that of Cube and P-oriented grains in a linear relationship as

N_NDcube=f_Cube·N_Cube + f_P·N_P                                  (4)

The samples annealed at 673-773 K (400-500 °C) are used for fitting, and the results are shown in Fig. 5. The C1-0/2/3 samples fit very well, while the samples B2 and C2 deviate more. The fitted values of f_Cube and f_P are 0.63 and 0.84, respectively. It seems that a linear correlation is a good approximation. The NDcube grains likely nucleate both by strain induced boundary migration (SIBM) similarly to Cube orientation and by PSN similarly to P orientation.

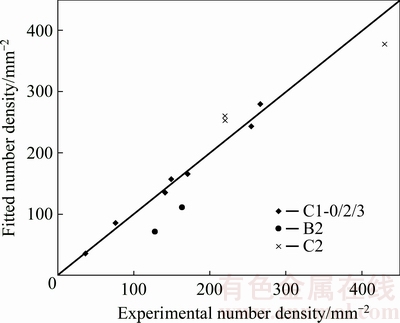
Fig. 5 Correlating number density of NDcube-oriented grains with that of Cube- and P-oriented grains according to Eq. (4)

Recrystallization nucleation is mainly attributed to SIBM and PSN mechanisms. Cube texture is usually formed by SIBM. Meanwhile, P is a typical orientation of PSN, and it is reasonable to assume that the fraction of P-oriented grains originating from PSN grains is almost constant under conditions of certain rolling strain when Zener drag effect is absent, regardless of annealing temperature and solute content. Then, the density of PSN is proportional to the density of P-oriented grains. The number density of all grains can be correlated linearly to the densities of Cube and P-oriented grains as

N_All=α_Cube·N_Cube+α_P·N_P                                      (5)

The fitted values of α_Cube and α_P are 7.2 and 67.7, respectively, and the results are shown in Fig. 6. The large value of α_P suggests that PSN dominates the nucleation of recrystallisation. Fitting C1-2 deviates most from the trend line, caused by Zener drag effect induced by pre-existing dispersoids. The value of α_P is almost ten times larger than α_Cube, and hence the overestimation for C1-2 is probably caused by the overestimation of α_P, implying that pre-existing dispersoids have a stronger effect on PSN than Cube. This is consistent with previous investigations showing that Cube-oriented subgrains are less affected by fine dispersoids due to their size advantage [23].

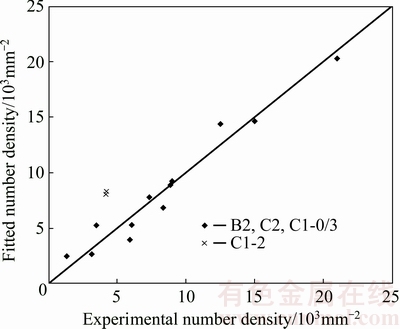
Fig. 6 Correlation of overall grain number density to that of Cube and P grains according to Eq. (5)

3.3 Effect of rolling strain on number density of recrystallised grains

Higher rolling strains induce more stored energy, reducing the critical radius for recrystallisation nucleation. Thus, the number densities of recrystallised grains increase with increased rolling strain. Simulations [15] suggest that the intensity of ND-rotated Cube in rolling texture increased with strain, indicating that more potential nucleation sites of ND-rotated Cube are formed in deformation zones. It is also reported that the possibility of finding P orientation in deformation zones increased from 27% to 39% as the rolling reduction is raised from 50% to 70%, while the possibility of finding NDcube decreased from 36% to 26% [12]. Figure 7 illustrates the effect of rolling strain on the grain number density of various orientations in C1-0. Recrystallisation finished within 5 s at 500 °C in the C1-0 alloy rolled by 50%-95%, and hence the effect of concurrent precipitation is negligible compared with annealing at lower temperatures. The results shown in Fig. 7 confirm that the higher rolling strain increases the nucleation density of recrystallisation, and special orientations such as P and NDcube follow a similar trend as Cube and other orientations. For instance, the number fraction of NDcube-oriented grains is constant, about 1.6%, for C1-0 rolled by 50%-95%. Figure 7 shows that the number fractions of P and NDcube grains are not influenced evidently by rolling strain in the range of 0.7-3 when the effect of precipitation is absent, although the number density increases with strain. Thus, the fitted equations obtained in Section 3.2 could be used for lower rolling strains if a scaling parameter is induced as a function of rolling strains, i.e.

N_ro=A_ro·exp(k_roε)                              (6)

where N_ro is the grain number density of special orientations (P, NDcube, Cube) or the overall grains; A_ro and k_ro are constants. The fitting values of k_ro are similar, about 0.7 for the overall, and the grains of P, NDcube and Cube orientations. It is indicated that the recrystallisation nucleation of special orientations follows a similar law as other orientations, when the effect of precipitation is negligible.

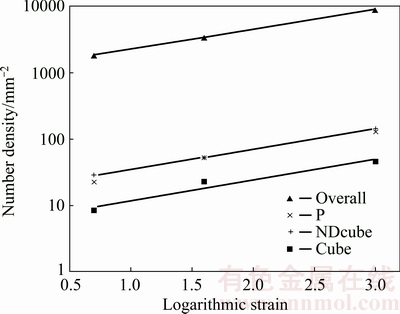
Fig. 7 Number densities of grains in C1-0 annealed at 500 °C for 5 s after various rolling strains

4 Conclusions

1) Statistical correlation suggests that the frequency of forming P grains at a particle larger than a critical diameter (about 1.1 μm) is about 2%. ND-rotated Cube grains are likely formed by both strain induced boundary migration (SIBM) and particle simulated nucleation (PSN), and their number density can be correlated linearly to that of Cube and P grains.

2) The overall grain number density can be linearly correlated to the number densities of Cube and P grains, which is helpful for modelling recrystallisation texture.

3) The number density of recrystallized grains is found to increase with the rolling strain following an exponential law. The number fractions of P and NDcube grains are insensitive to rolling strain when the effect of precipitation is absent.

References

[1] Humphreys F J. The nucleation of recrystallization at second phase particles in deformed aluminium [J] Acta Metallurgica, 1977, 25: 1323-1344.

[2] Humphreys F J, HATHERLY M. Recrystallization and related annealing phenomena [M]. Amsterdam: Elsevier, 2004.

[3] Zhao Q, Holmedal B. Influence of dispersoids on grain subdivision and texture evolution in aluminium alloys during cold rolling [J]. Transactions of Nonferrous Metals Society of China, 2014, 24: 2072-2078.

[4] Huang K, LI Y J, Marthinsen K. Isothermal annealing of cold-rolled Al-Mn-Fe-Si alloy with different microchemistry states [J]. Transactions of Nonferrous Metals Society of China, 2014, 24: 3840-3847.

[5]  ZIMINA M, CIESLAR M. Effect of pre-annealing on microstructure evolution of TRC AA3003 aluminum alloy subjected to ECAP [J]. Transactions of Nonferrous Metals Society of China, 2016, 26: 627-633.

[6] MAO W, YANG P. Formation mechanisms of recrystallization textures in aluminum sheets based on theories of oriented nucleation and oriented growth [J]. Transactions of Nonferrous Metals Society of China, 2014, 24: 1635-1644.

[7] Vatne H E, Shahani R, NES E. Deformation of cube-oriented grains and formation of recrystallized cube grains in a hot deformed commercial AlMgMn aluminium alloy [J]. Acta Materialia, 1996, 44: 4447-4462.

[8] Daaland O, Nes E. Recrystallization texture development in commercial Al-Mn-Mg alloys [J]. Acta Materialia, 1996, 44: 1413-1435.

[9] Tangen S,  K, Furu T, Nes E. Effect of concurrent precipitation on recrystallization and evolution of the P-texture component in a commercial Al-Mn alloy [J]. Metallurgical and Materials Transactions A, 2010, 41: 2970-2983.

[10] HUANG K, MARTHINSEN K, ZHAO Q L, LOGE R E. The double-edge effect of second-phase particles on the recrystallization behaviour and associated mechanical properties of metallic materials [J]. Progress in Materials Science, 2018, 92: 284-359.

[11] Liu W C, Morris J G. Effect of hot and cold deformation on the P {011}<455> recrystallization texture in a continuous cast Al-Mn-Mg aluminum alloy [J]. Scripta Materialia, 2006, 54: 2095-2099.

[12]  C, Gottstein G. The origin and development of the P{011}<111> orientation during recrystallization of particle- containing alloys [J]. International Journal of Materials Research, 2011, 102: 1106-1114.

[13] Mishin O V, Juul Jensen D, Hansen N. Evolution of microstructure and texture during annealing of aluminum AA1050 cold rolled to high and ultrahigh strains [J]. Metallurgical and Materials Transactions A, 2010, 41: 2936-2948.

[14] Zhao Q L, Huang K, Li Y J, Marthinsen K. Orientation preference of recrystallization in supersaturated aluminum alloys influenced by concurrent precipitation [J]. Metallurgical and Materials Transactions A, 2016, 47: 1378-1388.

[15]  C, Song J, Gottstein G. Modeling of texture evolution in the deformation zone of second-phase particles [J]. Acta Materialia, 2009, 57: 1026-1034.

[16] Huang K, Engler O, LI Y J, Marthinsen K. Evolution in microstructure and properties during non-isothermal annealing of a cold-rolled Al-Mn-Fe-Si alloy with different microchemistry states [J]. Materials Science and Engineering A, 2015, 628: 216-229.

[17] Vatne H E, Furu T,  R, Nes E. Modelling recrystallization after hot deformation of aluminium [J]. Acta Materialia, 1996, 44: 4463-4473.

[18] Crumbach M, Goerdeler M, Gottstein G. Modelling of recrystallisation textures in aluminium alloys: I. Model set-up and integration [J]. Acta Materialia, 2006, 54: 3275-3289.

[19]  C, Mohles V., Gottstein G. Modeling of non-isothermal annealing: Interaction of recrystallization, recovery, and precipitation [J]. Acta Materialia, 2011, 59: 6574-6587.

[20] Sidor J J, Decroos K, Petrov R H, Kestens L A I. Evolution of recrystallization textures in particle containing Al alloys after various rolling reductions: Experimental study and modeling [J]. International Journal of Plasticity, 2015, 66: 119-137.

[21] Huang K, Wang N, LI Y J, Marthinsen K. The influence of microchemistry on the softening behaviour of two cold-rolled Al-Mn-Fe-Si alloys [J]. Materials Science and Engineering A, 2014, 601: 86-96.

[22] Muggerud A M F , LI Y J, Holmestad R. Composition and orientation relationships of constituent particles in 3xxx aluminum alloys [J]. Philosophical Magazine, 2014, 94: 556-568.

[23] Engler O, Vatne H E, Nes E. The roles of oriented nucleation and oriented growth on recrystallization textures in commercial purity aluminium [J]. Materials Science and Engineering A, 1996, 205: 187-198.

含颗粒铝合金再结晶的择优取向晶粒数量密度的关联性

赵庆龙¹，张辉迪¹，Ke HUANG²，Knut MARTHINSEN³

1. 吉林大学 材料科学与工程学院 汽车材料教育部重点实验室，长春 130025；

2. Laboratory of Thermomechanical Metallurgy - PX Group Chair, Ecole Polytechnique Federale de Lausanne, Neuchatel CH-2002, Switzerland;

3. Department of Materials Science and Engineering, Norwegian University of Science and Technology, Trondheim 7491, Norway

摘  要：采用EBSD技术研究Al-(Mn)-Fe-Si合金等温退火后的再结晶晶粒结构。统计研究表明，在无沉淀反应条件下，在大于临界直径(约1.1 μm)的颗粒相周围形成P取向({011}<566>)晶粒的频率约为2%。晶粒总数量密度与P、立方取向({001}<100>)晶粒的数量成线性关系。再结晶晶粒的总数量密度及典型取向(P、ND旋转立方{001}<310>、立方)晶粒的数量密度随轧制应变量增加而增加，并服从指数规律。

关键词：再结晶织构；铝合金；颗粒激发形核；EBSD

(Edited by Bing YANG)

Foundation item: Project (20160520116JH) support by the Science and Technology Development Program of Jilin Province, China; Project supported by Key Laboratory of Automobile Materials (Ministry of Education), Jilin University, China; Project supported by PX group EPFL,  Switzerland; Project (193179/I40) supported by the Research Council of Norway

Corresponding author: Qing-long ZHAO; Tel: +86-431-85094699; E-mail: zhaoqinglong@jlu.edu.cn;

Ke HUANG; Tel: +41-21-6954472; E-mail: ke.huang@epfl.ch

DOI: 10.1016/S1003-6326(18)64654-0