DOI: 10.11817/j.issn.1672-7207.2016.10.011

基于双MRF模型的夜间图像增强方法

赵宏宇，肖创柏，禹晶

(北京工业大学 计算机学院，北京，100124)

摘要：为了获得更理想的夜间可视效果，通过分析Retinex算法在图像增强时存在的问题，提出一种基于双马尔科夫随机场(MRF)模型的单幅夜间图像增强算法。该算法首先在HSV颜色空间下构造边缘保持的Gaussian-MRF模型对照度分量进行估计，根据Retinex原理获得仅包含物体本身特性的反射分量，并通过增益补偿方法对亮度进行恢复与校正，然后构造Huber-MRF模型对增强结果进行优化，经过颜色空间转换后，最终实现夜间图像的增强。研究结果表明：本文算法增强效果显著，能够有效地凸显边缘细节信息，恢复图像的真实颜色，抑制暗区域噪声，削弱“光晕伪影”的影响，改善夜间图像质量。

关键词：MRF；Retinex原理；图像增强；HSV颜色空间；Huber-MRF模型

中图分类号：TP394.1             文献标志码：A         文章编号：1672-7207(2016)10-3361-08

Night color image enhancement based on dual MRF model

ZHAO Hongyu, XIAO Chuangbai, YU Jing

(College of Computer Science and Technology, Beijing University of Technology, Beijing 100124, China)

Abstract: Through analyzing the errors introduced by Retinex algorithms, a novel enhancement method based on dual Markov random field model(MRF) was proposed to improve single night color image visibility. Firstly, an edge-preserving Gaussian-MRF model to estimate illumination component in HSV color space was constructed. The reflection component obtained by Retinex principle was corrected through gain/offset method. Then, an effective Huber-MRF model to optimize the result was constructed. Finally, after the color space conversion, the proposed method realized the night color image enhancement. The results show that this method has the characteristics of detail preserving, color restoration, Halo effect elimination and noise suppression, and can enhance night color image visibility robustly.

Key words: MRF; Retinex principle; image enhancement; HSV color space; Huber-MRF model

在夜间环境下，计算机视觉监控设备采集的低照度图像严重退化，可视性较差，不仅信噪比和对比度都较低，甚至会出现较明显的颜色偏移和失真，大大降低了应用价值，因此，研究夜间图像增强算法具有重要的实际意义。夜间图像增强技术的目标是恢复场景的真实色彩和细节，并将图像调整到更适合人眼观察和计算机分析处理的范围，主要包括图像融合的方法和传统的图像增强方法。图像融合主要应用在近红外或微光成像技术方面，需要在同场景下采集多幅不同频谱的图像，算法复杂耗时，难以满足人们的实时要求；传统的图像增强方法能够适用于单幅图像的视觉效果改善上，可应用在彩色图像、非固定视角等多种场合，主要方法包括直方图的方法、同态滤波、基于Retinex理论^[1-7]的方法(后面简称Retinex算法)、基于小波的方法等。其中，Retinex算法对于处理夜晚、大雾等低可视度图像都有不错的效果，因而有着广阔的应用前景。Retinex理论是由LAND等于20世纪70年代提出的一种基于人类视觉的光亮度和色彩感知模型^[1]。由于Retinex算法具有高动态范围压缩，局部对比度增强，保持图像色彩恒常性等特点，所以引起了大量国内外学者的兴趣。LAND于1986年提出了最早的中心环绕(center/surround)Retinex算法，在此基础上，JOBSON等^[2-3]提出了单尺度Retinex(single-scale Retinex，SSR)算法和多尺度Retinex(multi-scale Retinex，MSR)算法。鉴于Retinex算法存在颜色失真的问题，JOBSON等^[4-5]随后提出了具有颜色保持能力的多尺度Retinex(multi-scale Retinex with color restoration，MSRCR)算法，该算法能够在扩大图像动态范围压缩的同时，实现颜色保真。KIMMEL等^[6]通过颜色空间的转化解决颜色失真的问题，提出了一种基于变分框架的Retinex算法。为了提高细节的显示效果，ELAD^[7]提出了基于双边滤波(Bilateral filter)的Retinex算法，该算法在保持图像细节的同时可以很好地消除光晕效应的影响。此后，基于Retinex原理的图像增强算法相继被提出，在效果与效率方面都有提高^[8-10]。目前对于夜间等低照度图像的增强方面，Retinex算法普遍存在噪声放大、高对比度边缘区域存在“光晕伪影”和颜色失真等问题。本文作者通过分析Retinex算法产生误差的原因，模拟人类视觉和大脑对图像的感知和理解的方式，提出了一种基于双马尔科夫随机场(MRF)的夜间图像增强算法。该算法在HSV(hue, saturation, value)颜色空间下仅对亮度图像进行处理，避免颜色失真；构建具有保边能力的Gaussian-MRF模型^[11]对照度分量进行估计，消除“光晕伪影”现象；根据Retinex原理获得反射分量，并通过增益补偿(gain/offset)方法对亮度进行恢复与校正；由于人类视觉对低频区域的噪声干扰比高频区域更加敏感，因此，构建Huber-MRF模型^[12-13]对增强结果进行优化，在抑制噪声的同时保留有效细节信息；最后经过颜色空间逆变换操作完成对图像的增强处理。本文算法能够克服Retinex算法处理夜间低照度图像时存在的多类问题，实现对较暗区域的动态范围进行拉伸，增强可视度，处理后的图像整体协调自然，更加符合人类观察特点。

1  Retinex理论与存在的问题

Retinex理论认为1幅图像可分为2部分，即1幅图像I可由反射分量R和照度分量L的乘积表示，

式中：x表示图像像素。照度分量的性质取决于光照的照射源，决定了图像中像素能达到的动态范围；反射分量的性质则取决于成像物体的特性，包含场景细节信息。Retinex原理的思想实际上就是去除或减少照度分量的影响，获得包含较多细节信息的反射分量。其计算过程在对数域上进行：

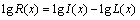
上述反射分量的求解在数学上是一个奇异问题，因此需要把求解问题变成约束最优化问题，通过对照度分量的准确估计进行反射分量的求解。本文采用中心环绕的方法对照度分量进行估计，中心环绕的方法假设每个像素的灰度值都受到来自周围环绕像素的影响，表示如下：

其中：*代表卷积操作；F(x)为环绕函数，一般采用高斯函数。为了保留更多的图像细节，环绕函数多选择具有保边能力的平滑滤波^[7]形式。

Retinex算法计算相对简单，但是在夜间图像的增强方面容易出现多类问题。本文将对直接影响反射分量求解的因素进行分析，首先分析照度分量估计的误差ΔL对于反射分量的影响，得到反射分量的求解误差为

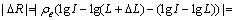
               (4)

式中：ρ_e为反对数函数；ΔR为计算反射分量的误差。

由式(4)可知：ΔL对于反射分量的准确求解具有一定的影响，但是并不是随着ΔL的增大而ΔR也明显增大。实际上，只有当ΔL很大时，才会对ΔR造成    影响。

考虑到图像中不可避免地存在着噪声干扰，设图像噪声为n，分析噪声对反射分量计算的影响。

  (5)

由式(5)可知：对于位于低灰度区域，处理后的结果噪声得到放大。根据式(4)可知：这些位于原图该区域的噪声基本不受到照度分量估计的影响。

以SSR算法为例，其环绕函数选择接近人眼感知的高斯函数形式：

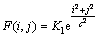             (6)

其中：K₁为常数；c为尺度参数，用于调控平滑程度；(i，j)为图像二维坐标。首先采用不同高斯核(见图1(c)和(d))对1幅具有较低动态范围的低照度图像进行增强，见图1(a)。当c较小时，低照度图像增强处理后的细节部分能较好地凸现出来，图像有一定程度上的颜色失真，见图1(e)；反之，当c较大时，获得的图像颜色保真度高，改善了低照度部分的亮度和对比度，但是出现了细节损失的情况，这在高亮区域尤为突出，见图1(f)。随着尺度参数c的增加，获得的增强结果趋于稳定，不产生大的变化，这与上述对式(4)的分析结果相符。

进行对于夜间图像增强处理的实验，结果见图1(b)。随着尺度参数c增加，图像可视度得到提升；当c增大到一定程度时，最终在一些暗区域(如天空区域等)出现了噪声放大的现象，此时c的变化趋势与噪声的强度变化相互独立，如图1(g)和(h)所示，这也与上述对式(4)和(5)的分析结果相符。同时，夜间图像受到非自然光源的影响，处理后的图像的高亮区域也会被放大，出现“光晕伪影”现象，如图1(g)和(h)所示的楼房灯源附近。

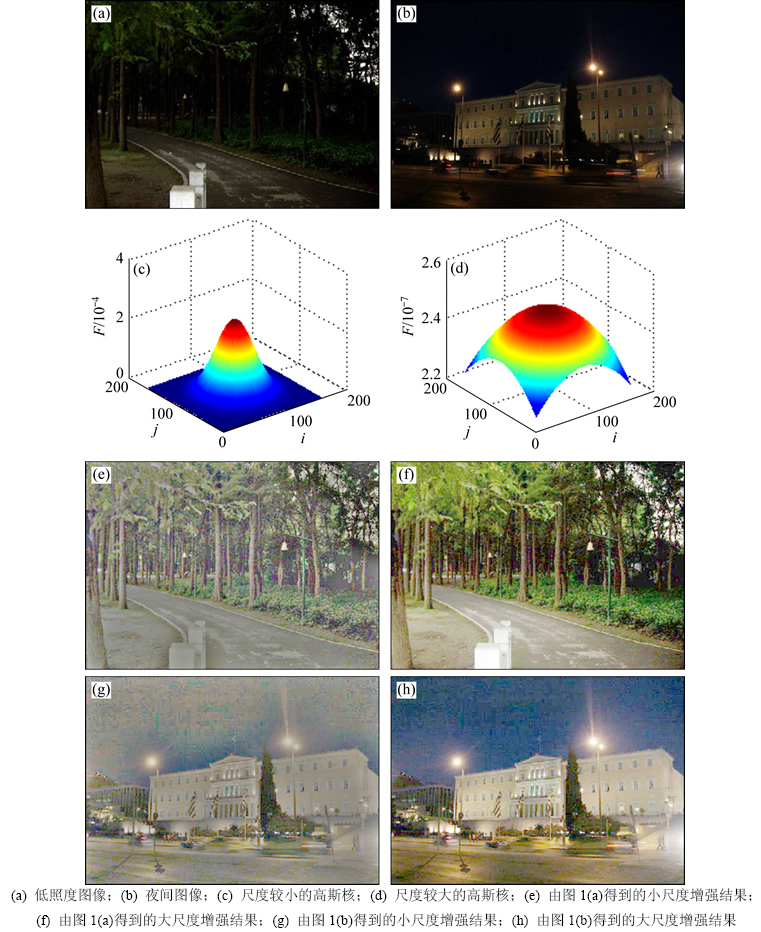
图1  Retinex算法增强效果

Fig. 1  Enhancement effects of Retinex algorithm

针对Retinex算法在图像增强方面存在的上述问题，本文主要对照度分量的估计与反射分量的优化2方面进行研究。求解照度分量时，将在保持边缘细节的基础上对局部进行平滑，力求提高图像低照度区域的可视度，并保持其高亮区域的细节信息；同时，对获得的反射分量结果进行优化，保持细节信息的前提下削弱噪声的强度。

2  本文算法

本文提出一种基于双MRF模型的单幅夜间彩色图像增强算法，该算法可分为3步：1) 进行颜色空间转化，将夜间彩色图像由RGB颜色空间转换到HSV颜色空间，获得图像在HSV颜色空间下的亮度图像，构建边缘保持的Gaussian-MRF模型估计图像照度分量，根据Retinex原理获得其反射分量；2) 采用增益补偿方法进行亮度恢复与校正；3) 构建Huber-MRF模型优化增强后的结果，将图像由HSV颜色空间转换到RGB颜色空间，最终得到理想的增强图像。

2.1  颜色空间转换

Retinex理论的应用前提是灰度世界假设(gray-world assumption)。在实际应用中，Retinex算法对于彩色图像的增强处理一般是在图像的R，G和B 3种颜色通道下分别进行，不同通道的不均衡增强容易造成图像颜色失真，且需要执行3次，时间复杂度较高。因此，本文选择在彩感知上更加接近人类视觉期望值的HSV颜色空间代替RGB颜色空间，将原图像转换到HSV颜色空间下，得到饱和度图像I_s、色调图像I_H和亮度图像I_V，这里仅对亮度图像进行增强处理。

2.2  基于Gaussian-MRF模型的照度分量估计

由于照度分量具有局部平滑的特性，本文构造具有保边平滑能力的Gaussian-MRF模型对原图进行平滑操作，从而估计出照度分量。该模型用于计算下述最大后验估计(MAP)问题：

        (7)

式中：I_V和L_V分别为原图像的亮度图像和亮度图像对应的照度分量；P(L_V)为先验概率，反映将要求解的L_V应具有的性质；P(I_V|L_V)为似然函数，表示图像噪声服从的分布，MAP目标就是在满足最大后验概率的条件下求出图像照度分量的估计值。该MAP问题的求解可以表示为最小化如下能量函数：

      (8)

本文通过构造包含数据项和平滑项的MRF模型来实现能量函数的求解。为调节参数，其值越大，平滑程度越高，取值范围为0.02~0.20。

该MRF模型的数据项定义如下

       (9)

式中：S为图像的像素集合；ρ_g为与σ₁有关的噪声分布函数，本文采用高斯分布，即ρ_g(u)=u²。

该MRF模型的平滑项定义如下：

 (10)

式中：T为像素x的相邻像素集；ρ_s为关于L_V的约束函数；本文取，为函数的平滑项上限，防止由于平滑项过大造成的边缘模糊的现象；w₁(x)为权值函数。该平滑项表示对相邻像素间一致性的约束，认为若像素处于同一深度，则它们的灰度越相似。

Retinex算法往往选择参数固定的滤波器对整幅图像进行照度分量估计，未考虑到光在场景传播时的指数衰减性，造成了图像增强效果层次性较差、细节损失的情况。虽然MSR和MSRCR等采用多尺度的方法克服细节恢复能力的不足，但是提高了算法的时空复杂度，且包含的参数较多。因此，需要在照度分量计算过程中考虑到场景信息的指数衰减性。式(10)中，设置权值函数为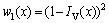，函数本身包含场景的深度信息，具有指数衰减的特性。设置权值的目的是力求增加低照度区域的平滑程度，并通过增加可视度较高的区域数据项的权重，在求解过程中保持已知场景的细节信息。

传统的SSR，MSR和MSRCR等算法在图像明暗对比强烈处易产生光晕现象，原因在于其对于光照平缓变化的假设。本文的Gaussian-MRF模型能够在实现局部平滑的同时较好地保持图像细节信息，避免由于高亮区域边缘过于平滑从而导致“光晕伪影”现象的产生。

2.3  增益补偿

当获得理想的照度分量L_V后，根据式(2)即可获得反射分量。此时，一般整体亮度偏暗，且对数域中的计算经常会出现负值，需要通过进一步调整以提高图像质量，本文采用增益补偿的方法对图像亮度进行恢复与校正，即

         (11)

其中：为调整后的反射分量图像；g为增益系数，用于放缩整体亮度；b为偏移量，用于避免出现负值的情况；γ为Gamma校正参数，取值范围为1~3，用于拉伸图像的动态范围。式(11)的处理实质上是为了去除中部分较低的非有效显示的图像信号，在达到较好的视觉效果的同时视觉信息损失最小。

2.4  基于Huber-MRF模型的优化操作

夜间图像中存在着较多的噪声，尤其是位于暗区域的物体存在较低的信噪比，在增强处理之后这些噪声也可能同时被放大。采用基于随机场模型的降噪技术能克服传统图像恢复方法的不足。因此，本文通过构建Huber-MRF模型来优化反射分量结果，采用MAP作为最优化准则，力求在保持边缘信息的前提下抑制噪声。与2.2节中相似，该MRF模型来自如下的能量函数：

      (12)

该MRF模型由数据项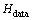和平滑项组成，为均衡数据项与平滑项的权重，其值越大，平滑程度越高，取值范围为0.001~0.020。

该MRF模型的数据项定义为

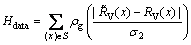       (13)

式中：R_V为目标图像；σ₂为尺度参数。

该MRF模型的平滑项定义如下：

 (14)

式中：ρ_h为由Huber函数，

   (15)

式(15)通过阈值T把函数分为线性和二次型2部分，既保护了边缘，又由凸性保证了MAP估计的有效性。当|u|≤T时，实际转化成了Gaussian-MRF模型，此时的二次型形式保证了局部平滑特性；当|u|＞T≥0时，线性形式保持了图像的边缘特性。P为斜率，用于调节保边程度。噪声等现象所处的局部背景亮度具有掩盖效应，亮度越大，噪声可见度越低，本文根据该特性，自适应调整Huber函数线性部分的斜率，以达到根据场景情况，合理地进行抑制噪声和保持边缘操作。定义P为

              (16)

式中：K₂为常数，用于调节斜率的影响强度。

在Huber-MRF模型下优化反射分量结果，不仅可以有效地抑制天空、远景等暗区域的噪声，而且能够减小图像边缘振荡，保持有效边缘细节。

当求解出理想的R_V后，结合饱和度图像I_s与色调图像I_H，将图像由HSV颜色空间变换转化到RGB颜色空间即可得到最终的增强图像R。

2.5  MRF模型的求解

MRF方法中寻求能量函数的最小解问题，可采用条件迭代模式(iterated conditional model，ICM)^[14]、置信度传播(belief propagation，BP)、模拟退火(simulated annealing，SA)、基于Graph Cuts的alpha-expansion^[15]等方法来实现。其中，ICM方法是一种易于操作的方法，具有较高的鲁棒性与可扩展性，本文采用ICM方法寻求能量函数的最优解。

本文的Gaussian-MRF模型力求在保持主要细节信息的同时，尽量对局部进行平滑，而Huber-MRF模型则是为了在平滑暗区域噪声的同时尽量保留细节信息。前者迭代次数n₁一般为3~10次，后者迭代次数n₂仅需要1~3次即可获得理想结果。

3  实验仿真与分析

本文在Matlab平台(CPU intel双核主频2.66 GHz)上对多幅彩色夜间图像进行分组实验，分别从主观视觉效果和图像质量客观评价2方面对其进行实验分析。本文将与多种基于Retinex原理的算法进行比较，包括SSR，MSR和MSRCR算法和ELAD等^[7]提出的基于双边滤波的Retinex算法。算法的主要参数设置包括：1) SSR参数参考^[2]；2) MSR参数参考^[3]；3) MSRCR的3个高斯尺度参数为σ₁=15，σ₂=80，σ₃=250，其他参数参考文献[4]；4) ELAD算法的双边滤波参数为P_l=5，σ_s=100，σ_r=0.3，Gamma参数为γ=5，其他参数参考文献[7]；5) 本文算法包含的参数设置为σ₁=200，λ₁=0.1，ω_min=0.8，g=1.2，γ=2，b=0，σ₂=200，λ₂=0.02，n₁=10，n₂=3。

在图像质量客观评价方面，本文采用图像均值、标准差、熵、边缘保持指数、直方图的相似度、峰值信噪比等评价指标对5种算法进行评价。均值用于评价图像平均亮度的变化，其值越大表示亮度提高越大；标准差用于评价图像的对比度，其值越大表示对比度越高；熵用于衡量图像的信息量，其值越大表示图像包含的信息越多；边缘保持指数用于衡量边缘的保持能力，其值越大表示其保持边缘能力越强，凸显细节能力也越强；直方图的相似度采用直方图的交来计算增强前后图像的RGB颜色直方图形状的相似程度，其值越大表示直方图越相似，算法的颜色保真能力越强； PSNR用于评价图像增强后噪声干扰情况，峰值信噪比值越大则表示抑制噪声的能力越强。

图2和图3所示为对真实场景下夜间彩色图像的增强处理实验，原图尺寸分别为550×400和512×384，其中，图2(b)~(f)所示分别为5种算法对图2(a)增强后的结果，图3(b)~(f)所示分别为5种算法对图3(a)增强后的结果。表1和表2所示为其对应的客观评价结果。图4所示为对模拟图像增强的比较实验，原图尺寸为512×512。图4(b)所示为图4(a)添加噪声后的结果，图4(c)所示为图4(b)添加70%透明度的阴影得到的结果，图4(d)~(h)所示分别为5种算法对图4(c)增强后得到的结果，表3所示为其对应的客观评价结果。由于Retinex算法处理低照度图像后，结果普遍存在泛白效果，图像整体亮度得到不同程度地提升。而亮度的变化为评价算法的重要指标，其值不同造成比较分析困难。因此，在对图3(a)增强的实验中采用线性调节的方法对实验结果亮度进行统一，即使其亮度近似相等，通过其他指标的比较进一步说明本文方法的优势。

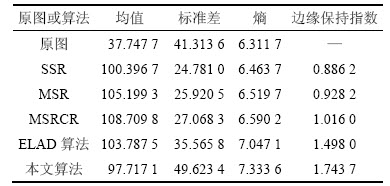
由表1~3可知：5种算法在一定程度上提高了均值，说明它们都在一定程度下增强了图像的亮度。由表1~3中的熵值与标准差值的分析可知：本文算法具有较强的对比度提升能力，并能够较好地丰富图像信息。同时，通过对表1与表2的EPI的观察，本文算法在保持边缘、凸显图像细节等方面均强于其他几种算法。同时，图2与图4的实验证明了SSR，MSR和MSRCR处理的结果容易出现泛白的现象。图3虽然对图像亮度进行了一定的调节，但是在亮度下降的同时，其他指标也跟着下降，图像质量并未得到显著改善。

图2  夜间图像增强效果的比较例子1

Fig. 2  Comparison example 1 of night image enhancing

表1  图2的客观评价

Table 1  Objective evaluation for Fig. 2

图3  夜间图像增强效果的比较例子2

Fig. 3  Comparison example 2 of night image enhancing

表2  图3的客观评价

Table 2  Objective evaluation for Fig. 3

本文算法与MSRCR均能够获得与原图更加接近的颜色效果，其增强效果更加明显，如图2(d)和(f)与图3(d)和(f)所示，说明本文算法与MSRCR均具有较强的颜色保真的能力。

通过对PSNR的比较分析可知：MSRCR抑制噪声方面比本文方法要好，但其环绕函数不具有边缘保持能力，因此，在一些较亮区域附近出现了“光晕伪影”现象，见图2与图3所示的灯光周围；而ELAD算法虽然消除了“光晕伪影”的影响，但其抑制噪声能力相对较弱，且在图像边缘出现了过度增强的现象；与之相比，结合主观观察分析，本文算法能够在保持良好细节信息的前提下抑制噪声的放大，削弱了“光晕伪影”的影响。

图4  对模拟图像的增强比较

Fig. 4  Comparison of simulated image enhancement

表3  图4的客观评价

Table 3  Objective evaluation for Fig. 4

总之，实验证明了本文算法与其他几种算法相比，可以很好地校正图像亮度，具有较强的对比度增强、细节恢复、颜色保持与抑制噪声等能力。

4  结论

1) 通过分析Retinex算法在图像增强时出现误差的原因，构造边缘保持的Gaussian-MRF模型对照度分量进行估计，较好地保持了细节信息，削弱了“光晕伪影”的影响。

2) 本文算法在HSV颜色空间下执行，使增强后的图像能很好地保持原有图像的颜色信息，避免了颜色失真的发生。

3) 针对暗区域噪声放大问题，通过构建Huber-MRF模型来优化反射分量结果，在保留细节信息的同时抑制了噪声，进一步提高了夜间图像质量。

参考文献：

[1] BANIC N, LONCARIC S. Light random sprays Retinex: exploiting the noisy illumination estimation[J]. Signal Processing Letters, IEEE, 2013, 20(12): 1240-1243.

[2] JOBSON D J, RAHMAN Z, WOODELL G A. Properties and performance of a center/surround Retinex[J]. IEEE Transactions on Image Processing, 1997, 6(3): 451-462.

[3] TAREL J, HAUTI N, CARAFFA L, et al. Vision enhancement in homogeneous and heterogeneous fog[J]. IEEE Intelligent Transportation Systems Magazine, 2012, 4(2): 6-20.

[4] JOBSON D J, RAHMAN Z, WOODELL G A. A multi-scale Retinex for bridging the gap between color images and the human observation of scenes[J]. IEEE Transactions on Image Processing, 1997, 6(7): 965-976.

[5] RAHMAN Z, JOBSON D J, WOODELL G A. Retinex processing for automatic image enhancement[J]. Journal of Electronic Imaging, 2004, 13(1): 100-110.

[6] KIMMEL R, ELAD M, SHAKED D, et al. A variational framework for Retinex[J]. International Journal of Computer Vision, 2003, 52(1): 7-23.

[7] ELAD M. Retinex by two bilateral filters[C]//Scale-Space 2005. Hofgeismar, Germany, 2005: 217-229.

[8] CHEN S, BEGHDADI A. Natural enhancement of color image[J]. Journal on Image and Video Processing, 2010, 175203: 1-19.

[9] WANG S, ZHENG J, HU H, et al. Naturalness preserved enhancement algorithm for non-uniform illumination images[J]. IEEE Transactions on Image Processing, 2013, 22(9): 3538-3548.

[10] 肖创柏, 赵宏宇, 禹晶. 基于引导滤波的Retinex快速夜间彩色图像增强技术[J]. 北京工业大学学报, 2013, 39(12): 1868-1873.

XIAO Chuangbai, ZHAO Hongyu, YU Jing. Rapid Retinex algorithm for night color image enhancement based on guided filtering[J]. Journal of Beijing University of Technology, 2013, 39(12): 1868-1873.

[11] PICKUP L C, CAPEL D P, ROBERTS S J, et al. Bayesian methods for image super-resolution[J]. The Computer Journal, 2009, 52: 101-113.

[12] PITCHAY S A, KABN A. Estimation of the regularisation parameter in Huber-MRF for image resolution enhancement[C]// IDEAL. Berlin, 2013: 294-301.

[13] KABN A, PITCHAY S A. Single-frame image recovery using a Pearson type VII MRF[J]. Neurocomputing, 2012, 80: 111-118.

[14] BESAG J. On the statistical analysis of dirty pictures[J]. J Roy Statist Soc B, 1986, 48: 259-302.

[15] FIX A, GRUBER A, BOROS E, et al. A graph cut algorithm for higher-order Markov random fields[C]//IEEE International Conference on Computer Vision. Barcelona, Spain, 2011: 1020-1027.

(编辑  杨幼平)

收稿日期：2015-10-15；修回日期：2016-01-08

基金项目(Foundation item)：北京市教委科技发展重点项目(KZ01210005007)；北京市教育委员会科技发展计划项目(KM201310005020) (Project(KZ01210005007) supported by Science and Technology Development Plan Key Project of Education Commission of Beijing Municipal; Project(KM201310005020) supported by Science and Technology Development Plan Project of Education Commission of Beijing Municipal)

通信作者：赵宏宇，博士，从事计算机视觉与图像处理研究；E-mail：asas.014@163.com