IMC based robust pid controller tuning for disturbance rejection
来源期刊:中南大学学报(英文版)2016年第3期
论文作者:Mohammad Shamsuzzoha
文章页码:581 - 597
Key words:PI/PID controller; step test; closed-loop response; IMC-PID; overshoot
Abstract: It is well-known that the IMC-PID controller tuning gives fast and improved set point response but slow disturbance rejection. A modification has been proposed in IMC-PID tuning rule for the improved disturbance rejection. For the modified IMC-PID tuning rule, a method has been developed to obtain the IMC-PID setting in closed-loop mode without acquiring detailed information of the process. The proposed method is based on the closed-loop step set point experiment using a proportional only controller with gain Kc0. It is the direct approach to find the PID controller setting similar to classical Ziegler-Nichols closed-loop method. Based on simulations of a wide range of first-order with delay processes, a simple correlation has been derived to obtain the modified IMC-PID controller settings from closed-loop experiment. In this method, controller gain is a function of the overshoot obtained in the closed loop set point experiment. The integral and derivative time is mainly a function of the time to reach the first peak (overshoot). Simulation has been conducted for the broad class of processes and the controllers were tuned to have the same degree of robustness by measuring the maximum sensitivity, Ms, in order to obtain a reasonable comparison. The PID controller settings obtained in the proposed tuning method show better performance and robustness with other two-step tuning methods for the broad class of processes. It has also been applied to temperature control loop in distillation column model. The result has been compared to the open loop tuning method where it gives robust and fast response.
J. Cent. South Univ. (2016) 23: 581-597
DOI: 10.1007/s11771-016-3105-1
Mohammad Shamsuzzoha
Department of Chemical Engineering, King Fahd University of Petroleum and Minerals, Dhahran 31261, Saudi Arabia
 Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Abstract: It is well-known that the IMC-PID controller tuning gives fast and improved set point response but slow disturbance rejection. A modification has been proposed in IMC-PID tuning rule for the improved disturbance rejection. For the modified IMC-PID tuning rule, a method has been developed to obtain the IMC-PID setting in closed-loop mode without acquiring detailed information of the process. The proposed method is based on the closed-loop step set point experiment using a proportional only controller with gain Kc0. It is the direct approach to find the PID controller setting similar to classical Ziegler-Nichols closed-loop method. Based on simulations of a wide range of first-order with delay processes, a simple correlation has been derived to obtain the modified IMC-PID controller settings from closed-loop experiment. In this method, controller gain is a function of the overshoot obtained in the closed loop set point experiment. The integral and derivative time is mainly a function of the time to reach the first peak (overshoot). Simulation has been conducted for the broad class of processes and the controllers were tuned to have the same degree of robustness by measuring the maximum sensitivity, Ms, in order to obtain a reasonable comparison. The PID controller settings obtained in the proposed tuning method show better performance and robustness with other two-step tuning methods for the broad class of processes. It has also been applied to temperature control loop in distillation column model. The result has been compared to the open loop tuning method where it gives robust and fast response.
Key words: PI/PID controller; step test; closed-loop response; IMC-PID; overshoot
1 Introduction
The proportional-integral-derivative (PID) controllers are the most widely accepted one in industrial applications at the regulatory level. The main reason for this is their comparatively simple structure, which can be readily understood and which allows them to be easily implemented in the real world. However, it has been noticed that many PI/PID controllers are not properly tuned and a lot of effort has been made to systematically resolve this problem. Therefore, the goal of this work is to develop a direct approach method of controller tuning from closed loop set point data.
There are varieties of PI/PID controller tuning approaches presented in the open literature and out of that two are extensively used for controller tuning, based either on open-loop or closed-loop plant tests; the majority of them being of the former type, employing the process gain (k), time constant (τ) and time delay (θ). The PID controller designed for the different types of processes based on direct synthesis [1] and Internal model control (IMC) are among such popular tuning methods [2-6]. The output response based on both the approaches has satisfactory performance and robustness. Recently, Vu and Lee [7], Rao and Chidambaram [8] and Shamsuzzoha et al [9] have developed analytical methods for the design of a PID controller cascaded with a second-order lead-lag filter for various types of time-delay processes for enhanced disturbance rejection.
Although the PI/PID tuning rule on the basis of IMC and direct synthesis methods gives excellent performance for setpoint changes, it shows slow output responses to input (load) disturbances for lag-dominant as well as integrating processes [3, 5, 10]. Skogestad [5] has modified the integral time in SIMC method which is an excellent remedy for processes with a large time constant to improve load disturbance rejection.
The above two-step approach is based on the open- loop test. It requires first to obtain process parameters and then calculate PI/PID tuning setting with any other existing tuning methods. There are two problems associated with this approach. First, to find out the process model with an open-loop experiment, usually a step test is desirable to get the process parameters. Sometimes it could be very tedious and may also disturb the process. The second problem associated with this is the approximation error in getting the parameters (for example, k, τ and θ) from the open loop step test data.
It is important to mention at this point that sometimes it is not easy to conduct open-loop test for the process model identification. There are always chances of the control variable drifting away from the specified value and eventually leading to products qualities off-specification. On the other hand, in the closed-loop test, it is easy to control the process during experiment and thus reduce the effect of disturbances.
The alternative of the open-loop approach is a two-step tuning procedure based on closed-loop setpoint experiment with a P-controller. It was originally proposed by Yuwana and Seborg [11], the method is applicable to most of the open-loop stable systems with dead time. Subsequently, the above method was modified by Jutan and Rodriguez [12], Lee [13], and Chen [14]. They identified a first-order with delay model by matching the closed-loop setpoint response with a standard oscillating second-order step response. Later, for the controller parameters calculation, they mainly utilized the Ziegler-Nichols tuning rules [15], which could give tight controller setting but other tuning rules, e.g., IMC-PID by Shamsuzzoha and Lee [3] could also be used. Lee et al [16] further reinvestigated the method [11] by identifying the processes with a second-order plus dead-time model under closed-loop conditions. They utilized the Taylor series expansion of the dead-time term with the combination of the ultimate data matching technique of Chen [14] for second-order plus dead-time model. However, the result of Lee et al [16] method gives relatively better performance and robustness over the other closed-loop methods [11-14], albeit at the expense of increased degree of complexity and computation.
In most of the above mentioned tuning methods based on the closed-loop two-step technique, at least five measurable quantities were required in the identification test to obtain the process model. For example, such methods [11, 13-14, 16] need to identify first peak of the output response (cp1), second peak of the output response (cp2), first minimum of the output response (cm1), half-period of oscillation (△t) and the steady-state value (c∞).
There are few problems associated with the above closed-loop experiment. 1) The required number of measurable quantities are high, i.e. at least five. 2) For the low value of overshoot, it is difficult to find the accurate value of the first minimum of the output response (cm1) and second peak of the output response (cp2) from the step test experiment. 3) To obtain the precise value of cm1 and cp2, one has to generate the output response of large overshoot with considerable oscillation. Furthermore, there are several problems associated with the large overshoots. It gives a long settling time and needs large input changes that are undesirable in chemical process industries.
The other alternative approach to both the above mentioned two step procedures is to use the one step closed-loop experiments, that directly obtain controller setting without finding process parameters. A very popular and old method is that of Ziegler-Nichols (Z-N) [15]. It needs only the ultimate controller gain (Ku) and the period of oscillations (Pu), which one can obtain directly from an experiment. For a PI-controller the recommended settings are Kc=0.45Ku and τI=0.83Pu. Ziegler-Nichols [15] closed-loop tuning method is still very widely used for controller tuning in industrial processes. However, there are several disadvantages of this method.
The most significant one is that in the Z-N method we actually push the process to the limit of instability as we search for the Ku. Creeping up on the ultimate gain can be very time consuming, but if we try to save time by making large adjustments in the search for the Ku, it is very likely that the process will actually become unstable, at least for a brief period.
The remedy for the above problem is to introduce the relay method of  and
and  [17], which requires the feature of switching on/off-control in the system. One more drawback is that the Z-N [15] tuning setting does not work satisfactorily on all processes. The prescribed controller settings are somewhat aggressive for lag-dominant (integrating) processes [18] and sluggish for dead time dominant process [5]. The third disadvantage of the Ziegler-Nichols method [15] is that it is not applicable to a simple second-order process.
[17], which requires the feature of switching on/off-control in the system. One more drawback is that the Z-N [15] tuning setting does not work satisfactorily on all processes. The prescribed controller settings are somewhat aggressive for lag-dominant (integrating) processes [18] and sluggish for dead time dominant process [5]. The third disadvantage of the Ziegler-Nichols method [15] is that it is not applicable to a simple second-order process.
Haugen [19] has developed the good gain method which is entirely on the basis of the trial and error approach to find the suitable controller gain and finally the tuning parameters. Hu and Xiao [20] have developed an analytical PI tuning method which is similar to the setpoint overshoot method [10]. Skogestad and Grimholt [21-22] have claimed that it is hard to obtain a better performance than SIMC, at least for PI control based on a first order with time delay model. Seki and Shigemasa [23] have proposed the method to retune the existing controller based on comparing the closed-loop responses. Veronesi and Visioli [24] have also claimed for retuning of an existing PI controller for better performance and robustness.
Recently, Alcantara et al [25] have addressed the model-based tuning of PI/PID controller based on the robustness/performance and servo/regulator trade-offs. The interesting feature of the study has been to show how to shift each compromise based upon constraint. They have extended the preliminary design concept of balanced autotuning which was published earlier [26]. K-SIMC method, a modification of SIMC rule has been proposed recently by Lee et al [27]. Torrico et al [28] proposed a new and simple design for the filtered Smith predictor (FSP), which belongs to a class of dead-time compensators (DTCs) and allows the handling of stable, unstable, and integrating processes. Recently, several authors [29-36] have proposed the modified approach for the enhanced PID controller design based on the open loop method.
In view of the above discussion about the different types of controller tuning approaches, it is clear that there is a need for a simple and effective controller tuning method in closed-loop.
Therefore, the goal of this work is to find a simple and direct controller tuning technique in closed-loop for the broad class of the processes. No detailed prior information of the plant process parameters (k, θ and τ) is required to get the modified IMC-PID controller [4] settings from the closed-loop setpoint experiment. It removes the shortcomings of the Ziegler-Nichols continuous cycling method and can be an able substitute for the same. Although the original IMC-PID controller tuning method is applicable only for the low order processes, the proposed closed loop method is used even in high order processes without any modification.
2 Modified IMC-PID controller tuning rule
2.1 IMC-PID controller design for first-order with dead time process
The motivation of this section is to review IMC-PID controller tuning proposed by Rivera et al [4] for first order process with time delay. In next section, this tuning method has been utilized as a basis for the development of the proposed closed-loop method. The first-order time delay process is commonly used as a representation of the process dynamics for several equipment in chemical industries as
 (1)
(1)
where k, τ and θ are the process gain, time constant and time delay, respectively. It is important to note that the PID controller gives reasonable response in the chemical industries and the same is given as
 (2)
(2)
where Kc, τI, τD and τF are the proportional gain, integral time constant, derivative time constant and lag filter of the PID controller, respectively. The other form of the PID structure (e.g., series form) can be easily transformed from the ideal form in Eq. (2) by using a simple calculation [1].
Figures 1(a) and (b) show the block diagram of the IMC control and equivalent classical feedback control structures, respectively. In this block diagram, g(s) is the process, 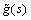 process model, q(s) IMC controller and c(s) the classical feedback controller. The remaining variables are the manipulated variable u, process output variable y, the setpoint ys, and the input disturbance d at the plant. The relationships in closed-loop from the setpoint and load disturbance to the output are
process model, q(s) IMC controller and c(s) the classical feedback controller. The remaining variables are the manipulated variable u, process output variable y, the setpoint ys, and the input disturbance d at the plant. The relationships in closed-loop from the setpoint and load disturbance to the output are
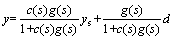 (3)
(3)
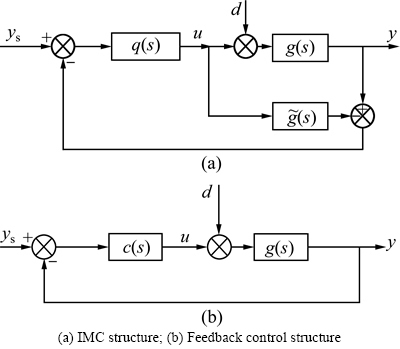
Fig. 1 Block diagram of IMC and classical feedback control systems:
The conventional feedback controller which is equivalent to the IMC controller can be expressed by
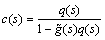 (4)
(4)
where  indicates the process model transfer function; c(s) is conventional and q(s) is the IMC controller. The standard IMC controller design is divided into two steps as
indicates the process model transfer function; c(s) is conventional and q(s) is the IMC controller. The standard IMC controller design is divided into two steps as
Step 1: The process model 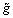 is decomposed into two parts:
is decomposed into two parts:
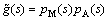 (5)
(5)
where pM(s) and pA(s) are the portions of the model inverted and not inverted, respectively, by the controller; pA(s) is typically a non-minimum phase which includes time delay and right half plane zeros; pA(0)=1.
Step 2: The typical IMC controller is given by
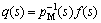 (6)
(6)
where f(s) is the IMC filter and given as  τc is closed loop time constant which controls the tradeoff between the performance and robustness. The parameter r is chosen to be a sufficiently big value to form the IMC controller semi-proper. Consider a first order process with time delay, the IMC controller is given as
τc is closed loop time constant which controls the tradeoff between the performance and robustness. The parameter r is chosen to be a sufficiently big value to form the IMC controller semi-proper. Consider a first order process with time delay, the IMC controller is given as
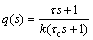 (7)
(7)
Therefore, the feedback controller c(s) which is equivalent to the IMC controller is
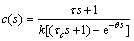 (8)
(8)
Consider approximation of the time delay expression in Eq. (8) using first-order Pade approximation i.e., 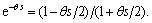 The resulting controller can be easily obtained by simple calculation in the form of PID with first order filter [4] as
The resulting controller can be easily obtained by simple calculation in the form of PID with first order filter [4] as
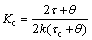 (9)
(9)
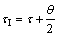 (10)
(10)
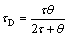 (11)
(11)
 (12)
(12)
The main reason of using 1/1 Pade approximation is to obtain both simple PID control structure with enhanced performance. It has been found that high order approximation of the dead time has not any significant advantage in terms of the performance and stability of the control system. The above PID controller offers fast and smooth set-point tracking, but has a sluggish disturbance rejection, especially for processes with a small time-delay/time-constant ratio [1, 3, 5, 10]. To enhance the load disturbance response, Skogestad [5] suggested the modification in integral time (τI) for lag dominant and integrating process as
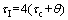 (13)
(13)
Incorporating the above recommended setting for the lag dominant (integrating) process, the integral time in Eq. (13) has been modified for the improved disturbance rejection for the small time-delay/time- constant ratio (integrating process) and given as
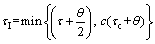 (14)
(14)
where c is an arbitrary constant and c=4 has been suggested by Skogestad [5], as we can see in Eq. (10). This modification of the τI has significant advantage for both the lag and delay dominant processes. The closed loop response has been shown for different value of c in Fig. 2. It is well known that in the majority of process control loops, the disturbance rejection is the most important task for the controller. To check the faster disturbance rejection, different values of c (c=4, 3 and 2) have been tested and it was found that c=3 is the most suitable choice for the modified tuning rule [19, 22]. The choice of c=3 has impact on the robustness of the system and it will be somewhat lower than c=4. The other impact should be on the overshoot in the setpoint response and it will be slightly higher for c=3. In Fig. 2, c=4 gives quite sluggish disturbance rejection response. In the modified tuning rules, selection of τc=0.6θ has been the recommended choice as it gives maximum sensitivity (Ms); approximately 1.73 for the integrating process, and Ms=1.75 for the delay dominant process. Therefore, the above tuning method can be simplified for the τc=0.6θ and given as
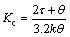 (15)
(15)
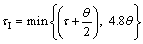 (16)
(16)
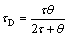 (17)
(17)
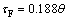 (18)
(18)
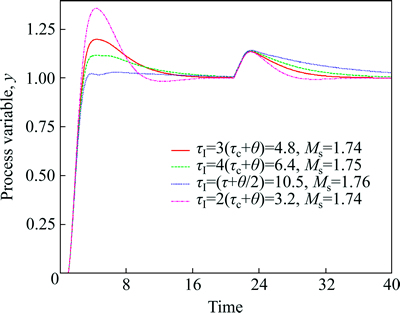
Fig. 2 Closed-loop responses of g(s)=e-s/(10s+1) for different value of τI(i.e, c=4, 3, 2 and τ+θ/2) while other tuning parameters (Kc, τD and τF) are same for τc=0.6θ. Setpoint change at t=0; load disturbance of magnitude 1 at t=20 (ys=1 and d=1)
2.2 Analysis of effect of integral action
The original IMC-PID rule (Eqs. 9-12) gives fast and smooth set-point tracking. However, it has a slow disturbance rejection for processes with a small θ/τ ratio. The modified tuning formula given in Eqs. (15)-(18) is for the enhanced disturbance rejection. To show the effect of the integral action, a first-order process with time delay g(s)=e-s/(10s+1) has been considered. Figure 2 shows the comparison of the closed-loop response of the modified IMC-PID controller for four different values of the τI while other tuning parameters (Kc, τD and τF) are kept constants. The different values of τI obtained by changing the value of c, i.e, c=4, 3 and 2. To test the performance of the control system, both the load disturbance and setpoint have been added a step change of magnitude 1 (ys=1 and d=1). The robustness measure, Ms-value is almost the same for all four closed-loop responses. Although the closed-loop response for the disturbance rejection of c=2 is better, it gives an unacceptable overshoot in setpoint response. The output response of the original IMC-PID (τI=τ+θ/2) gives slow disturbance rejection while satisfactory setpoint change as shown in figure. The goal of the proposed modification in the IMC-PID controller is to obtain fast disturbance rejection while maintaining the sepoint response.
Therefore, c=3 is a better choice of the integral time and resulting integral time equation is given as τI=3(τc+θ), which is tradeoff between load performance and setpint change.
2.3 Effect of setpoint filter on servo response
The integral action has increased in the modified IMC-PID tuning rule for the enhanced disturbance rejection. This modification is applicable to the lag-dominant and integrating process with time delay. It provides satisfactory improvement in the disturbance rejection performance while deteriorate setpoint response with large overshoot. Therefore, lead–lag setpoint filter which is the usual practice in industries to improve the servo response, is recommended to remove the overshoot in setpoint response. The recommended choice to lead-lag filter is fr=(0.75τIs+1)/(τIs+1). To show the performance improvement a first order process with time delay g(s)=e-s/(10s+1) has been considered. The resulting set–point filter for this case should be fr=(3.6s+1)/(4.8s+1). Figure 3 shows the closed-loop response of the modified IMC-PID tuning rule for both with and without set–point filter. The integral of the absolute value of the error (IAE)-value is reduced from 3.11 to 2.44 and total variation (TV) from 14.73 to 11.47, after using the setpoint filter. As expected, the output response with set–point filter is fast without any overshoot.
2.4 Effect of low order lag filter in closed-loop response
The modified IMC-PID tuning has first order lag filter τF=0.188θ. These days most of the DCS systems usually provide the PID controllers with various equations, lead lag blocks, filter blocks and pure dead time blocks. Some, however, may allow you to select a more sophisticated filter. It is straightforward to implement the modified IMC-PID with lag filter control scheme under the modern DCS system environment. As an example, a standard block of “first-order lag” in a well-known DCS system is:
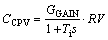 (19)
(19)
where Ti is first-order log time (Ti=1-Scan period); I is first-order log time setpoint; s is Laplace transform operator.
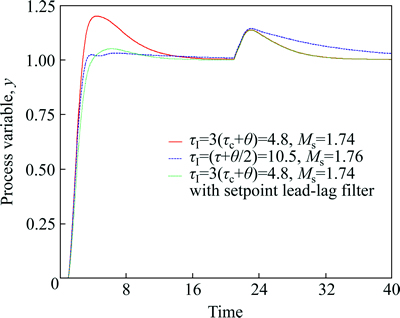
Fig. 3 Effect of setpoint filter to remove overshoot from setpoint response (Setpoint responses of first-order stable process with time delay g(s)=e-s/(10s+1); Setpoint change at t=0; load disturbance of magnitude 1 at t=20)
The selection of the right filter parameter always ensures the overall performance improvement of the control loop. Especially, in the PID controller when the derivative action is active, if the lag-filter is not used, or if its magnitude is very small, then the controller will be responding to noise. This may cause the control valve to move unnecessarily and eventually lead to process upset. On the other hand, if a filter parameter is large, then it may slow the performance of the controller. Therefore, it is important to select a proper value of the lag-filter so that the controller responds quickly to any upsets in the process.
The recommended setting of the filter parameters should not be more than 1/3 of the process dead time [37]. In the modified IMC-PID, τF=0.188θ for τc=0.6θ, which is within the recommended value.
In this work, the simulation study is based on the ideal form of controller which is given in Eq. (2). In real practice one has to modify derivative action with the derivative filter τDs/(ατDs+1) in the PID control.
A simulation is carried out to show the effect of the lag-filter in the system that possesses noise in the measurement. A first order process with time delay g(s)=e-s/(10s+1) has been considered for the simulation and controller setting is calculated based on τc=0.6θ. In this comparison, the derivative-filter is used in both the controllers, with and without lag-filter, with α=0.1. Figure 4 shows the comparison of the closed-loop process response and control variable of the modified IMC-PID controller. The resulting process variables and the control variables are plotted for the controller with and without first order lag filter with noise measurement of white noise of power 2.0×10-5.
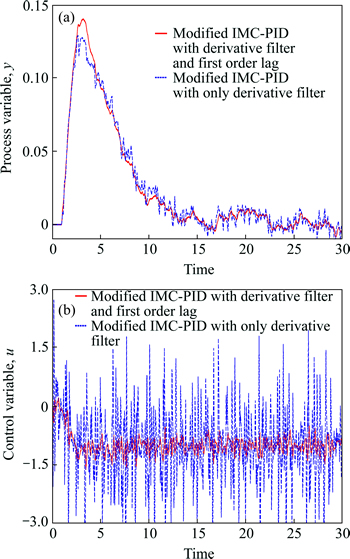
Fig. 4 Load disturbance response (with noise measurement) of first-order with time delay process g(s)=e-s/(10s+1). The controller tuning parameters are selected for τc=0.6θ and the resulting PID setting of the proposed method is 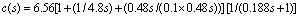 with white noise of power 2.0×10-5. For the modified IMC-PID without lag-filter
with white noise of power 2.0×10-5. For the modified IMC-PID without lag-filter 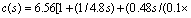
 load disturbance of magnitude 1 at t=0
load disturbance of magnitude 1 at t=0
The derivative filter, which is also included in both the cases, plays an important role in reducing the measurement noise. It is clear from Fig. 4 that the control output is less noisy for the modified IMC-PID with output-filtered structures. This is because the proportional action is partially responsible for the amplification of the measurement noise [38]. Therefore, the control structure with lag-filter which is applied to the whole control variable is more efficient than that applied to the derivative action only.
3 Closed-loop setpoint step test experiment
This section describes the procedure to find the closed-loop data for the proposed IMC-PID controller tuning method. The easy and classical approach for closed-loop experiment is a setpoint step response given in Fig. 5. In this experiment one can keep full control of the process, including the change in the output variable. The time tp to reach the first overshoot and its magnitude is the simplest to observe in this experiment.

Fig. 5 Step test output response in closed-loop with P-only control
The closed-loop data extraction procedure is as follows [39]: 1) Switch the controller to P-only mode (for example, increase the integral time τI to its maximum value or set the integral gain KI to zero). This kind of controller mode switch does not upset the industrial process.
2) Make a setpoint change that gives an overshoot between 0.10 (10%) and 0.60 (60%); about 0.30 (30%) is a good value. Record the controller gain Kc0 used in the experiment. Most likely, unless the original controller is quite tightly tuned, one will need to increase the controller gain to get a sufficiently large overshoot.
It is important to note that most of the time it is difficult to extract the required information accurately from small overshoots (novershoot<0.10). Therefore, this experiment does not consider the overshoot less than 0.1. On the other hand, large overshoots (novershoot>0.6) give severe oscillations and long settling time and also require more excessive input changes. For these reasons, it is recommended to use an “intermediate” overshoot of about 0.3 (30%) for the closed-loop setpoint experiment.
3) From the closed-loop setpoint response experiment, obtain the following values (see Fig. 5):
① Controller gain used in step test, Kc0
② Overshoot=(△yp-△y∞) /△y∞
③ Time from setpoint change to reach first peak output (overshoot), tp
④ Relative steady state output change, b=△y∞/△ys.
The resulting output variables are given as
Setpoint change: △ys=ys–y0;
Peak output change (at time tp): △yp=yp–y0;
Steady-state output change after setpoint step test: △y∞=y∞-y0.
It is important to note that one can speed up the experiment and there is no need to wait for the response to settle. The waiting time could be more if the overshoot in the experiment is somewhat large (novershoot>0.4). In such circumstances, it is recommended to finish the experiment once the output process response reaches its first minimum. In the next step, record the corresponding output, △yu and calculate △y∞ with following relationship.
△y∞=0.45(Δyp+Δyu) (20)
The detailed derivation of the relationship in Eq. (20) is available in Ref. [10].
4 Mathematical correlation between closed- loop data and IMC-PID
The main purpose of this research is to find a simple technique to obtain IMC-PID controller setting in closed- loop mode. Therefore, the aim is to develop a mathematical correlation between the setpoint response data (Fig. 5) and the modified IMC-PID settings (Eqs. (15)-(18)) with τc=0.6θ. For this reason, 15 first- order with time delay models g(s)=ke-θs/(τs+1) that cover a wide range of processes have been considered. They cover a broad range of processes from dead time dominant to lag-dominant (integrating) as
τ/θ=0.10, 0.20, 0.40, 0.80, 1.0, 1.50, 2.0, 2.50, 3.0, 5.0, 7.50, 10.0, 20.0, 50.0, 100.0
It is possible to scale time with respect to the time delay (θ) and since the closed-loop response depends on the product of the process and controller gains (kKc) we have without loss of generality used in all simulations k=1 and θ=1.
For each of the 15 process models (values of τ/θ), we have obtained the modified IMC-PID settings using Eqs. (15)-(18) with the choice τc=0.6θ. Furthermore, for each of the 15 processes, we have generated 6 closed- loop step setpoint responses using P-controllers that give a wide range of fractional overshoots as:
novershoot=0.10, 0.20, 0.30, 0.40, 0.50 and 0.60
In total, we have 90 setpoint responses, and for each of these we have recorded data for four variables as:
The P-controller gain Kc0 used in the experiment, the fractional overshoot, the time to reach the overshoot (tp), and the relative steady-state change, b=△y∞/△ys.
4.1 Selection of controller gain (Kc)
The first goal is to find a correlation between the above four data and the corresponding IMC-PID controller gain Kc. Figure 6 shows the plot between kKc verses kKc0 for 90 setpoint experiments for different values of τ/θ ratio. As one can see from the said figure that the ratio Kc/Kc0 is approximately constant for a fixed value of the overshoot. It is independent of the value of τ/θ ratio and therefore it is given as:
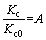 (21)
(21)
where the ratio A is a function of the overshoot only. In Fig. 7, we plot the value of A, which is obtained as the best fit of the slopes of the lines in Fig. 6, as a function of the overshoot. The equation below (solid line in Fig. 7) fits the data in Fig. 6, nicely and it is given as
A=1.45(novershoot)2-2.02novershoot+1.27 (22)
Therefore, the final relationship for the controller gain is given as
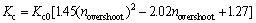 (23)
(23)
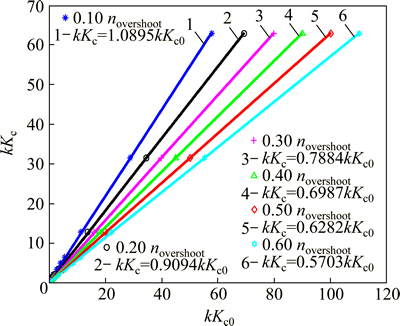
Fig. 6 Plot between experimental P-controller gain kKc0 and corresponding PID controller gain kKc in Eq. (15)
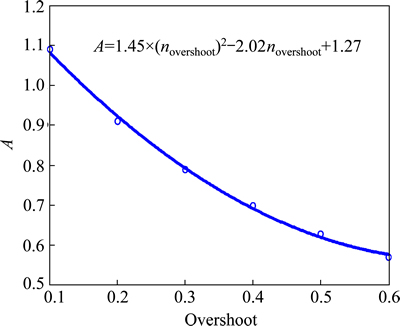
Fig. 7 Plot of variation of A with fractional overshoot using slopes data from Fig. 6
4.2 Selection of integral time (τI)
The purpose of this section is to find a simple correlation for the τI. The modified IMC-PID tuning rule in Eq. (16) uses the minimum of two τI values. It would be interesting to search a similar correlation for both the large and small delay in closed-loop method as well.
1) Comparatively large time delay process (τI1=τ+θ/2): It is the case of relatively large delay and the integral time in the IMC-PID tuning rule is τI=(τ+θ/2). After rearrangement of Eq. (15)
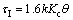 (24)
(24)
In Eq. (24), there is a requirement of process gain k, and to this effect it may be written as:
kKc=kKc0·Kc/Kc0 (25)
The closed loop gain kKc0 for the P-control setpoint experiment can be calculated from the value of b as:
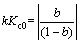 (26)
(26)
The τI relationship can be obtained by substituting kKc from Eq. (25) and Kc/Kc0=A into Eq. (24), as
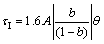 (27)
(27)
To show the steps in brief, the closed-loop setpoint response is Δy/Δys=g(s)c(s)/(1+g(s)c(s)). With a P-controller (gain Kc0), the steady-state value is Δy∞/Δys= kKc0/(1+kKc0)=b and we derive Eq. (26). The absolute value is included to avoid problems if b>1, as they may occur sometimes because of imprecise data.
It is feasible to get the value of time delay θ directly from the closed-loop setpoint response. Moreover, this is not always straightforward. Shamsuzzoha and Skogestad [10] have developed a reasonable correlation for the dead time θ and the setpoint peak time tp which is direct and easier to observe.
For processes with a relatively large time delay, the ratio θ/tp varies between 0.27 (for τ/θ=8 with overshoot=0.1) and 0.5 (for τ/θ=0.1 with all overshoots), as evident from Fig. 8 for the intermediate overshoot of 0.3, the ratio θ/tp varies between 0.32 and 0.50. A conservative choice would be to use θ=0.5tp because a large value increases the integral time. However, to improve the performance for processes with smaller time delays, we propose to use θ=0.43tp, which is only 14% lower than 0.50 (the worst case).
In summary, we have for a process with a relatively large time delay:
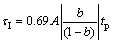 (28)
(28)
2) Comparatively small time delay process (τI2=4.8θ). The integral time for a lag-dominant (integrating) process is given as
τI2=4.8θ (29)
For τ/θ>4.8, it can be seen from Fig. 8 that the ratio θ/tp varies between 0.25 (for τ/θ=100 with overshoot=0.1) and 0.37 (for τ/θ=8 with overshoot 0.6). We select the average value θ=0.305tp which is approximately 17% lower than 0.37 (the worst case). Also note that for the intermediate overshoot of 0.3, the ratio θ/tp varies between 0.30 and 0.32. In summary, we have for a lag- dominant process:
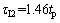 (30)
(30)
Thus, it comes the conclusion. The integral time τI is obtained in a similar way as Eq. (16) and it is the minimum of the above two values as
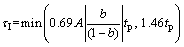 (31)
(31)
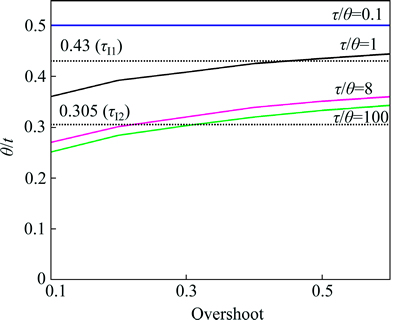
Fig. 8 Ratio of process time delay (θ) and setpoint overshoot time (tp) as a function of overshoot for four first-order with delay processes (solid lines). Dotted lines: Values of θ/tp used in final correlations.
4.3 Derivative action (τD)
In this section, a method has been proposed to obtain the τD from the closed-loop step test data with P-only controller.
Mode I: The process which is close to integrating i.e., τ>>θ, integral time is τI=4.8θ in IMC-PID tuning formula, and θ=0.305tp in the closed-loop. τD1 in Eq. (17) can be approximated as
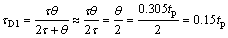 (32)
(32)
Mode II: For the processes which have τ≤θ, integral time is τI=(τ+0.5θ) in IMC-PID, and equivalent to this information in closed-loop, θ=0.43tp. Assuming τ=θ, τD2 is calculated from Eq. (17) as
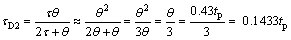 (33)
(33)
It is clear from the above analysis that τD1 and τD2 are very close to each other and the conservative pick of τD should be:
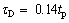 (34)
(34)
4.4 Low order controller filter from step test data
The modified IMC-PID method has low order lag filter τF=τcθ/[2(τc+θ)], and it simplifies to τF=0.188θ for τc=0.6θ.
The objective of this section is to find the equivalent lag filter τF from closed-loop data. The analytical equation of the first order filter (τF=0.188θ) for the integrating process is τF=0.188θ=0.188×0.305tp=0.057tp.
The lag filter for the relatively large delay is τF=0.188θ=0.188×0.435tp=0.082tp. The lag filter has significant impact on the processes with relatively small delay (integrating process). Therefore, the final recommended value for the lag-filter in the modified tuning method is given as
τF=0.057tp (35)
5 Guidelines for selection of initial controller gain Kc0
Although the proposed method is valid for the overshoot between 0.10 to 0.60, the recommended value of overshoot around 0.3 gives almost similar response to IMC-PID. Therefore, it is important to have guidelines for it.
Initial controller setting Kc01 is applied and resulting overshoot 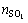 is achieved, which is somewhere between 0.1 to 0.60 but not around 0.30. The desired overshoot and P-controller gain are OS and Kc0, respectively. In this method, the aim is to get the same performance of the PID tuning rule regardless of the overshoot that resulted in closed-loop experiment. In theory, calculated Kc for any overshoots from different closed-loop setpoint tests should be the same and one can write a mathematical relationship as
is achieved, which is somewhere between 0.1 to 0.60 but not around 0.30. The desired overshoot and P-controller gain are OS and Kc0, respectively. In this method, the aim is to get the same performance of the PID tuning rule regardless of the overshoot that resulted in closed-loop experiment. In theory, calculated Kc for any overshoots from different closed-loop setpoint tests should be the same and one can write a mathematical relationship as
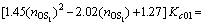
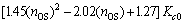 (36)
(36)
Equation (36) provides a guideline for the P-controller gain for the subsequent closed-loop setpoint test. The resulting equation can give initial controller setting for overshoot around 0.3 as
 (37)
(37)
It is important to note that we are not keen to obtain the exact fractional overshoot of 0.30, so in a few trials one can achieve the desired overshoot (around 0.3) from Eq. (37).
6 Simulation study
In this section, results of the simulation study have been discussed for the different types of processes. The investigated models have been studied by many reseachers [2, 3, 5, 9-10, 40-43].
In the simulation study, several performance and robustness matrices have been calculated and compared with other methods. The simulation results of 13 different processes are listed in Table 1 which clearly shows that the proposed method provides acceptable controller settings in all the cases. The performance and robustness of the control system are evaluated by the following indices:
Output performance (y) is quantified by computing the integrated absolute error, 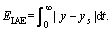 Manipulated variable usage is quantified by calculating the total variation (VT) of the input (u), which is the sum of all its moves up and down. If we discretize the input signal as a sequence [u1, u2, u3 …, ui …] then
Manipulated variable usage is quantified by calculating the total variation (VT) of the input (u), which is the sum of all its moves up and down. If we discretize the input signal as a sequence [u1, u2, u3 …, ui …] then 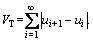 VT is a good measure of the smoothness of the signal. To estimate the robustness, we calculate the maximum closed-loop sensitivity, defined as Ms=maxω|1/[1+gc(jω)]|. Since Ms is the inverse of the shortest distance from the Nyquist curve of the loop transfer function to the critical point (-1, 0), a small Ms-value indicates that the control system has a large stability margin. The optimistic approach is to have a small value of EIAE, VT and Ms at the same time, but for a well-tuned controller there is a trade-off, which means that a reduction in EIAE implies an increase in VT and Ms and vice versa.
VT is a good measure of the smoothness of the signal. To estimate the robustness, we calculate the maximum closed-loop sensitivity, defined as Ms=maxω|1/[1+gc(jω)]|. Since Ms is the inverse of the shortest distance from the Nyquist curve of the loop transfer function to the critical point (-1, 0), a small Ms-value indicates that the control system has a large stability margin. The optimistic approach is to have a small value of EIAE, VT and Ms at the same time, but for a well-tuned controller there is a trade-off, which means that a reduction in EIAE implies an increase in VT and Ms and vice versa.
Three different overshoots (approximately 0.1, 0.3 and 0.6) have been considered and the PI/PID settings obtained, based on step response experiments. The same is compared with the recently published methods [10] for all process models. Although comparison has been done for three different overshoots, the results have been listed only for the case of overshoot around 0.3 in Table 1. The closed-loop performance evaluation has been done by introducing a unit step change in both the set-point and load disturbance, i.e (ys=1 and d=1).
The results of three methods has been compared and shown in Fig. 9-13 for cases 3, 5, 9, 10 and 11. For both the proposed and setpoint overshoot method [10], overshoot around 0.3 is compared with the modified IMC-PID method. The proposed controller setting response shows smaller overshoot and faster disturbance rejection than the setpoint overshoot method [10]. The closed–loop response for both the set–point tracking and disturbance rejection confirms that the proposed method gives better response.
Table 1 Comparison of proposed PID controller setting with setpoint overshoot method
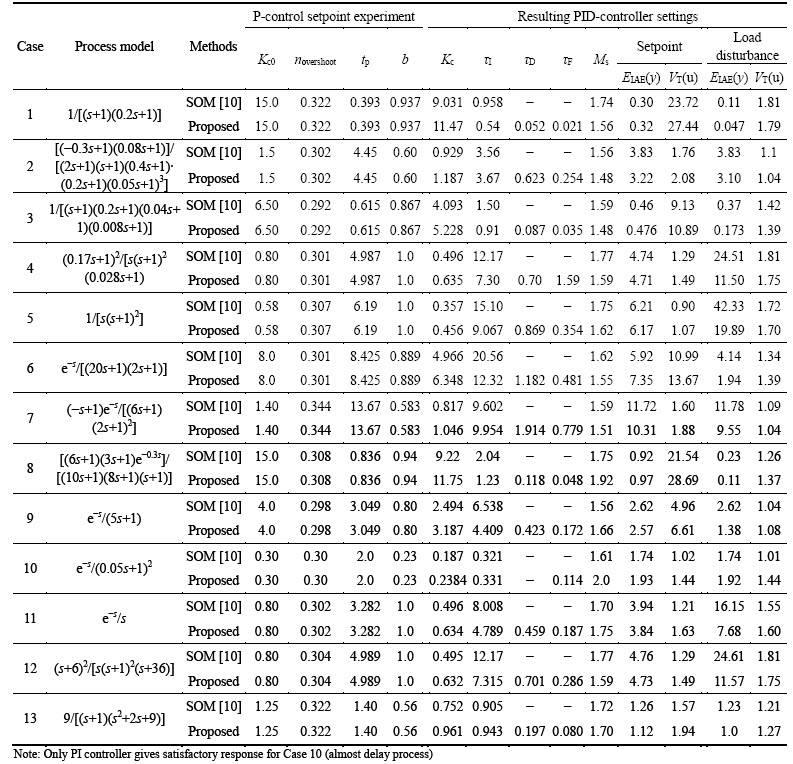
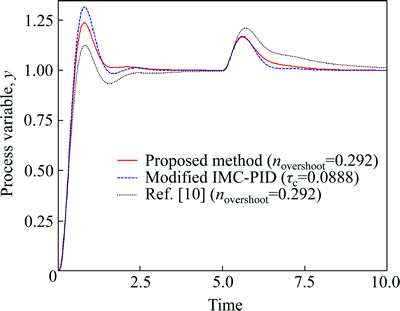
Fig. 9 Closed loop response of g(s)=1/[(s+1)(0.2s+1)(0.04s+1)· (0.008s+1)] (case 3) (Setpoint change at t=0; load disturbance of magnitude 1 at t=5)
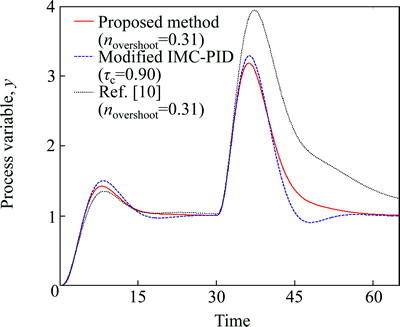
Fig. 10 Closed loop responses of g(s)=1/s(s+1)2 (case 5) (setpoint change at t=0; load disturbance of magnitude 1 at t=30)

Fig. 11 Closed loop responses of g(s)=e-s/(5s+1) (case 9) (setpoint change at t=0; load disturbance of magnitude 1 at t=25)

Fig. 12 Closed loop responses of g(s)=e-s/(0.05s+1)2 (case 10) (setpoint change at t=0; load disturbance of magnitude 1 at t=8)
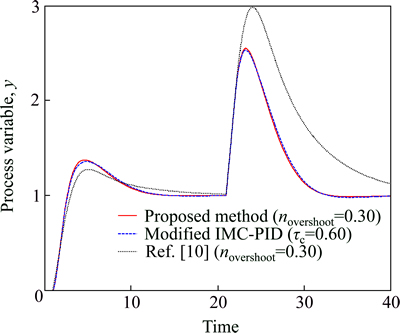
Fig. 13 Closed loop responses of g(s)=e-s/s (case 11) (setpoint change at t=0; load disturbance of magnitude 1 at t=20)
The above presented closed-loop method is on the basis of modified IMC-PID tuning method. The comparison has been also performed to check the agreement of the proposed method with the modified IMC-PID tuning method. In all the above cases (Fig. 9-13) response of the modified IMC-PID is also shown which clearly indicates that the proposed method is perfectly matched with the modified IMC-PID method.
The lower overshoot of around 0.10 usually gives sluggish and more robust PID controller settings in the proposed method, while a large overshoot, close to 0.6, gives more aggressive and fast PID-settings.
6.1 Comparison with two-step open-loop method
6.1.1 Example 1: Distillation column model
Distillation is a widely used separation method in the process industries. Its operation is extremely critical, because of the purity demand of the products. The process model for the level control in distillation is given by the delay integrating process. The distillation column model [3, 40, 43] was considered
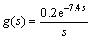 (38)
(38)
The IMC based two-step method of Chien and Fruehauf [40], closed-loop method by Shamsuzzoha and Skogestad [10] and the proposed method of the present study were used to design the PID controller. The performance indices are listed in Table 2, and output response in Fig. 14 for both the unit step change in setpoint and disturbance rejection. It is clear from Table 2 and Fig. 14 that the proposed tuning rule results in the least settling time for disturbance rejection, followed by that of Chien and Fruehauf [40]. It is important to note that both the proposed and setpoint overshoot methods [10] are based on the closed-loop test and they do not require the process model to design PID controller like Ref. [40]. The above discussion indicates that the suggested method has clear benefit over the other methods.
6.1.2 Example 2: Boiler steam drum
The process of boiler steam drum is an example of an integrating process with inverse response which has the following process transfer function [41].
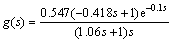 (39)
(39)
The PID controllers were designed using the proposed method and the setpoint overshoot method [10] based on the closed-loop test for an overshoot of around 0.61. The other two well-known model based methods [2, 41], are also tested and compared with the proposed method. Figure 15 shows the closed-loop output responses for a unit step change introduced in both the setpoint and load disturbance. The controller setting parameters including the performance indices are listed in Table 2. Figure 14 shows that the proposed method gives better response than that obtained from the method of Ref. [10]. Although Luyben’s [41] method gives a smaller peak, it has slow response and takes long time to settle. It is important to note that the process model is required to obtain the controller settings for both the model based methods [2, 41].
Table 2 Comparison of performance and robustness of the proposed method with other well-known methods
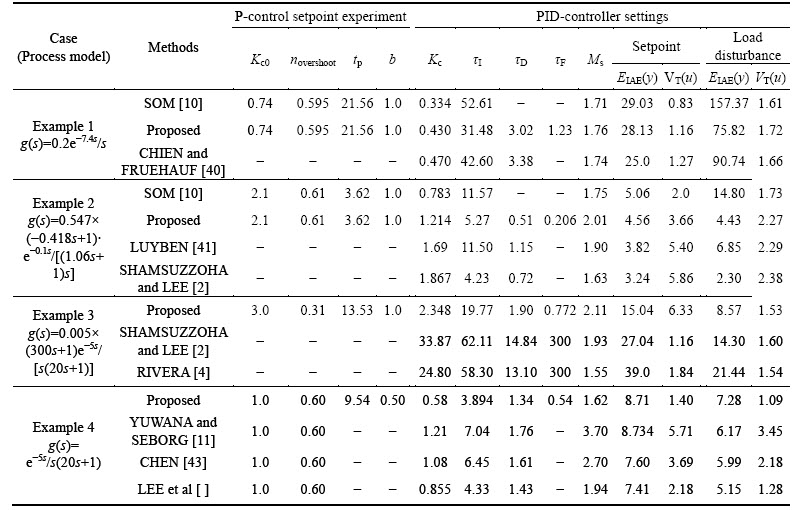
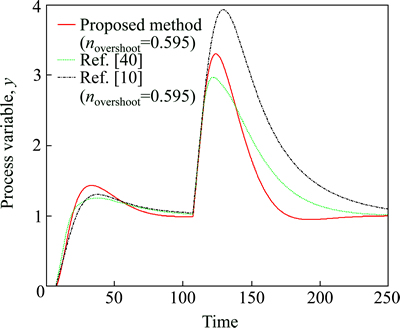
Fig. 14 Closed loop responses of distillation column model g(s)=0.2e-7.4s/s (Example 1) (setpoint change at t=0; load disturbance of magnitude 1 at t=100)
6.1.3 Example 3: Paper machine dryer cans model
Consider the following process of paper machine dryer cans [2, 42].
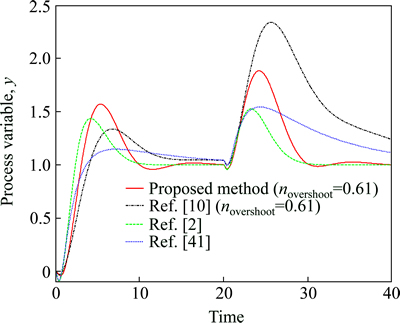
Fig. 15 Closed loop responses of boiler steam drum model g(s)=0.547(-0.418s+1)e-0.1s/[1.06s+1)s] (Example 2) (setpoint change at t=0; load disturbance of magnitude 1 at t=20)
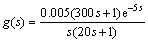 (40)
(40)
The PID controller parameter settings for the proposed method based on the closed-loop test for overshoot 0.31 and those of Refs. [2] and [4] are presented in Table 2. The PID controller settings for the latter two methods were taken from Ref. [2]. Figure 16 shows the closed-loop output responses for a unit step change introduced in both the setpoint and load disturbance for these three design methods.
Shamsuzzoha and Lee [2] previously demonstrated the superiority of their method over those of Rivera et al [4] and [42]. Figure 16 clearly shows that Rivera et al’s method of Ref. [4] has a large overshoot and long settling time. The proposed method shows a clear advantage over the others and exhibits a lower IAE value and fast settling time with small overshoot in disturbance rejection.

Fig. 16 Closed loop responses of paper machine dryer cans model g(s)=0.005(300s+1)e-5s/s(20s+1) (Example 3) (setpoint change at t=0; load disturbance of magnitude 1 at t=150)
On the basis of the above discussion it is clear that the controller settings of the proposed method provide satisfactory performance and robustness for regulatory problems for a broad class of processes.
6.2 Comparison with two-step closed-loop method
The proposed method is also compared with the two-step procedure based on closed-loop setpoint experiment with a proportional controller (Kc0). In most of the two-step tuning procedures, first they identify a first-order with time delay model by equating the closed- loop setpoint response with a standard oscillating second-order step response. Once the model parameters are obtained, one can use any well-known tuning method, e.g., IMC-PID tuning rule [2]. The proposed method is a direct approach for the controller setting parameters and identification of few parameters is required. Probably the simplest to observe in the closed-loop experiment are the time tp to reach the (first) overshoot and its magnitude.
To compare the results of both the direct proposed method and the two-step method based on closed-loop test, a high order process with significant time delay has been considered below as
Example 4:  (41)
(41)
The PID controller setting data of Refs. [11, 14, 16] were taken from Ref. [16] for the initial controller setting Kc0=1. In the proposed method Kc0=1 is also selected to obtain the PID setting. The performance and robustness matrix is listed in Table 2. The performance of the all four methods is compared and shown in Fig. 17. The figure shows that the proposed tuning method gives acceptable performance with high robustness. For the same value of Kc0, the proposed method gives significantly robust (Ms=1.62) closed-loop response with very low value of VT compared to the other methods. The same observations have been found for the several other processes, though they are not shown.
Figure 18 shows the manipulated variable (MV) response for example 4 as the representative case. The response shows that the proposed method has smooth controller output with less effort in comparison with the other methods. The value of VT is significantly less for the proposed method among all the others.
On the basis of the above discussion it is again clear that the proposed method scores over the other two-step closed-loop tuning methods for a broad class of the processes.
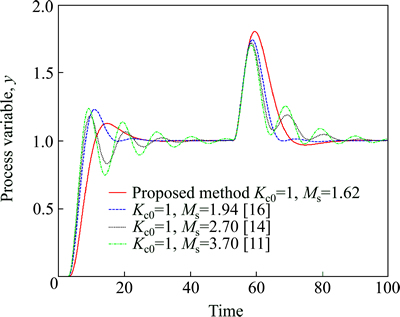
Fig. 17 Closed loop responses of g(s)=e-3s/[(2s+1)(s+1)2] (Example 4), Setpoint change at t=0; load disturbance of magnitude 1 at t=50)
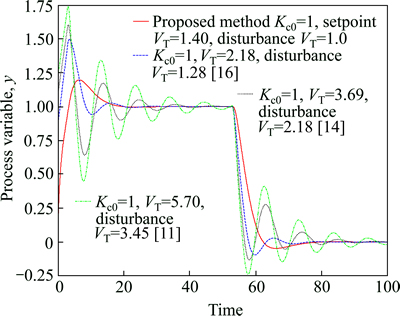
Fig. 10 MV plots of g(s)=e-3s/[(2s+1)(s+1)2] (Example 4) (setpoint change at t=0; load disturbance of magnitude 1 at t=50)
6.3 Robustness test
It is important to perform a comparison on fair basis for all the tuning methods. It can be achieved only if the performance comparison is done for the same level of robustness, e.g. same Ms-value. The other approaches for the investigation of the robustness of all compared methods are to check the closed-loop response with uncertainty in different process parameters. Therefore, the robustness of the different controllers are evaluated by inserting a perturbation uncertainty in all the three parameters (k, θ and τ). To show the closed-loop response of the model mismatch, a high order process with time delay (example 4) has been considered. A case has been selected for 50% in the dead time uncertainty and 25% in both the gain and time constant simultaneously towards the worst case model mismatch, as follows 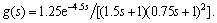 The simulation results for the plant-model mismatch are given in Fig. 19 for both the servo and regulatory problems. It should be mentioned that the controller settings used in simulation are those calculated for the process with nominal process parameters. It is clear from Fig. 19 that the proposed controller tuning method has an excellent setpoint and load response for model mismatch. Although the closed-loop response for both Refs. [11, 14] two-step methods is not shown in the said figure, it give an unstable oscillatory response. The better closed-loop response for the nominal case by Lee et al [16] two-step controller tuning method is achieved by sacrificing the robustness of the closed-loop system.
The simulation results for the plant-model mismatch are given in Fig. 19 for both the servo and regulatory problems. It should be mentioned that the controller settings used in simulation are those calculated for the process with nominal process parameters. It is clear from Fig. 19 that the proposed controller tuning method has an excellent setpoint and load response for model mismatch. Although the closed-loop response for both Refs. [11, 14] two-step methods is not shown in the said figure, it give an unstable oscillatory response. The better closed-loop response for the nominal case by Lee et al [16] two-step controller tuning method is achieved by sacrificing the robustness of the closed-loop system.

Fig. 19 Effect of parameters uncertainties in both proposed and Lee et al [2] methods. Modified process with 50% high θ, 25% high k and 25% low τ from original value of Example 4, g(s)=1.25e-4.5s/[(1.5s+1)(0.75s+1)2]: Setpoint change at t=0; load disturbance of magnitude 1 at t=50
6.4 Application to distillation column
The case study demonstrates the application of the proposed tuning method in the distillation column temperature control loop. The dynamic model of the distillation column in Aspen-Hysys is selected from Ref. [44] to show the simplicity and effectiveness of the proposed method.
is selected from Ref. [44] to show the simplicity and effectiveness of the proposed method.
The depropanizer column considered in this case study produces a distillate product that is 98% (molar fraction) propane. At 110°F, the vapor pressure of propane is slightly higher than 200 psia. Therefore, an operating pressure of 200 psia is kept in the condenser. The boiler pressure is estimated by assuming a pressure drop over each tray of 5 inches of liquid in this high- pressure column. The liquid density of this hydrocarbon system is about 30 lb/ft3. The column has 30 trays and is fed on tray 15, and the pressure in the reboiler is 202.6 psia.
The column feed is 100 lb-mol/hr of a mixture (molar fraction) of propane (30%), isobutene (40%) and n-butane (30%) at 90°F. The specified purity of distillate is 98% propane. The specified impurity of propane in the bottoms is 1.0%. The design reflux ratio is 3.22 and the design reboiler heat input is 1.02×106 Btu/hr.
Luyben [44] suggested Reflux-Vapor Boilup (RV) control structure of the depropanizer and is shown in Fig. 20. The suggested tuning parameters of the different loops are kept unchanged except the temperature loop. The flow controller has Kc=0.5, τI=0.3 min, and two level controllers Kc=2.0 each. The pressure controller is tuned using normal slow setting with Kc=1.0 and the integral time is τI=20.0 minutes. For the temperature loop, Luyben [44] applied relay-feedback test and found ultimate gain (Ku=32) and the ultimate period (Pu=7.3 min). Finally he obtained the PI setting using the TL [18] method as Kc=10.0 and τI=16.0 min.
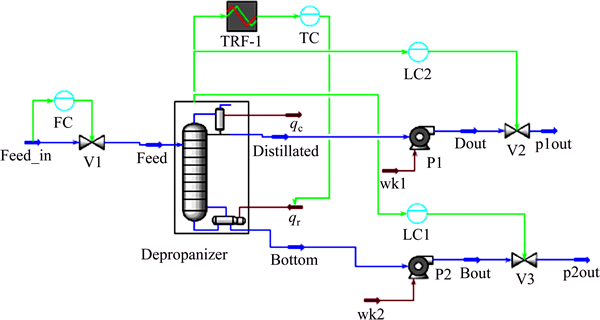
Fig. 20 Depropanizer column flowsheet with controllers installed (pressure controller is not shown in main flowsheet, and it is installed in sub-flowsheet)
In the proposed method, overshoot around 0.30 gives satisfactory performance and robustness. Start the test in closed-loop using a P-controller with gain Kc0. The magnitude of the gain Kc0 should be selected such that it gives overshoot around 0.30 for a setpoint change of magnitude Δysp. From the setpoint experiment, read off the maximum response, yp, the steady state response y∞, and the time to reach the first peak (tp). It is assumed that the process output has value y0 before the setpoint change occurs. Step test in temperature loop is shown in Fig. 21.

Fig. 21 closed-loop responses with P-controller (controller gain Kc0=8.0) of a depropanizer temperature loop
Process output before the setpoint change (y0)=125.7°F, and manipulated variable (OP)=50.60%, a step test is conducted for setpoint change (Δys)=ys–y0=130.7-125.7=5.0, with the P-controller of Kc0= 8.
Note: It is important to eliminate the impact of the integral action in the step test and for that substitute τI=1000 (sufficiently large value).
Based on the closed-loop setpoint response to a step change of amplitude △ys=5°F as shown in Fig. 22, the overshoot and other parameters are calculated as
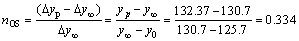
The relative steady-state change of the process output is:
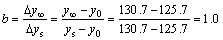
It shows that the process is almost integrating and the value of peak time tp=107.83-100.0=7.83 min. The PID parameter settings can be calculated as
A=1.45(nOS)2–2.02nOS+1.27=1.45(0.334)2-2.02(0.334)+ 1.27=0.757

For the integral time,
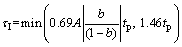
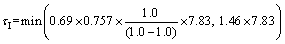
τI=11.43 min
τD=0.14×tp=0.14×7.83=1.10 min
The effectiveness of the proposed method has been checked for the setpoint change in the temperature loop and closed-loop response is shown in Fig. 22. The response is significantly fast and smooth without any oscillation.
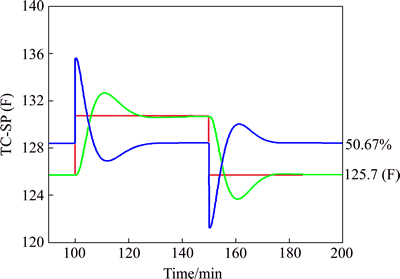
Fig. 22 closed-loop setpoint responses of depropanizer temperature loop with a PID-controller (setpoint change of magnitude 5°F at t=100 min; reverse setpoint change of magnitude -5°F at t=150 min)
The proposed closed-loop method has been compared with the modified IMC-PID controller for disturbance rejection. The results for the two disturbances in feed flowrate are shown in Fig. 23. At 15 min the feed is increased from 100 to 120 lb-mol/hr and at 120 min a large change in the feed flow rate is made, and is finally dropped to 80 lb-mol/hr. Figure 23 clearly shows the advantage of the proposed method in disturbance rejection. Although the proposed method is based on the modified IMC-PID tuning rule, it gives better and more robust closed-loop response. It seems that the proposed method is less sensitive with approximation error in different parameters during step test, whereas modified IMC-PID is very sensitive with the time delay measurement.
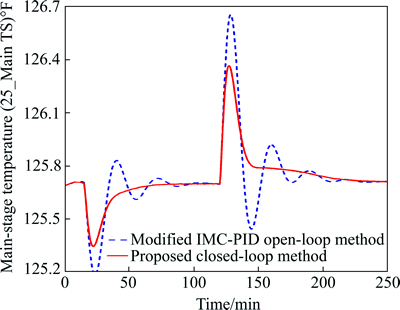
Fig. 23 Closed-loop response for step changes in feed flow rate as a disturbance at t=15 min from 100 to 120 lb-mol/hr, at 120 min from 120 to 80 lb-mol/hr
7 Conclusions
1) The integral time has been modified for the classical IMC-PID controller design and it is recommended to use 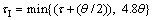 for Ms=1.74.
for Ms=1.74.
2) A closed-loop tuning method has been developed for the IMC-PID controller setting using step test in setpoint change. The experiment is conducted in closed-loop using a P-controller with gain Kc0. The PID-controller settings are then obtained directly from the following data from the setpoint experiment: overshoot, (Δyp-Δy∞) /Δy∞; time to reach first peak, tp; relative steady state output change, b=Δy∞/Δys. The steady state value can be calculated by Δy∞=0.45(Δyp+ Δyu) for fast completion of the experiment.
3) The proposed PID tuning with lag filter is: Kc=Kc0A,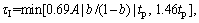 τD=0.14tp, τF=0.057tp, A=[1.45(novershoot)2-2.02novershoot+1.27].
τD=0.14tp, τF=0.057tp, A=[1.45(novershoot)2-2.02novershoot+1.27].
4) The method is valid with satisfactory results for overshoot around 0.1 to 0.6, an overshoot of around 0.3 is recommended for the best performance and robustness.
5) The initial controller gain which provides overshoot around 0.3 in closed-loop test can be calculated from the following equation as
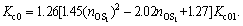
6) The simulation results illustrate the better performance and robustness of the proposed method for different classes of processes. A simple closed-loop step test is required to obtain the IMC-PID controller setting which gives the appropriate controller settings for acceptable performance and robustness for a broad range of process models.
Acknowledgement:
The author would like to acknowledge the support provided by King Abdulaziz City for Science and Technology (KACST) through the Science & Technology Unit at King Fahd University of Petroleum and Minerals (KFUPM) for funding this work through project number 11-ENE1643-04 as part of the Notional Science Technology and Innovation Plan.
References
[1] Seborg D, Edgar T, Mellichamp D. Process dynamics and control [M]. New York: Wiley, 2004.
[2] Shamsuzzoha M, Lee M. PID controller design for integrating process with time delay [J]. Korean Journal of Chemical Engineering, 2008, 25: 637-645.
[3] Shamsuzzoha M, Lee M. IMC-PID controller design for improved disturbance rejection of time-elayed processes [J]. Ind Eng Chem Res, 2007, 46: 2077-2091.
[4] Rivera D, Morari M, Skogestad S. Internal model control. 4. PID controller design [J]. Ind Eng Chem Process Des Dev, 1986, 25: 252-265.
[5] Skogestad S. Simple analytic rules for model reduction and PID controller tuning [J]. journal of Process Control, 2003, 13: 291-309.
[6] Shamsuzzoha M, Lee M. Design of advanced PID controller for enhanced disturbance rejection of second order process with time delay [J]. AIChE, 2008, 54: 1526-1536.
[7] Vu T, Lee M. A unified approach to the design of advanced proportional-integral-derivative controllers for time-delay processes [J] Korean Journal of Chemical Engineering, 2013, 30: 546-558.
[8] Rao A, Chidambaram M. Enhanced two-degrees-of-freedom control strategy for second-order unstable processes with time delay [J]. Industrial and Engineering Chemistry Research, 2006, 46: 3604-3614.
[9] Shamsuzzoha M, Lee S, Lee M. Analytical design of PID controller cascaded with a lead-lag filter for time-delay processes [J] Korean Journal of Chemical Engineering, 2009, 26: 622-630.
[10] Shamsuzzoha M, Skogestad S. The setpoint overshoot method: A simple and fast closed-loop approach for PID tuning [J]. Journal of Process Control, 2010, 20: 1220-1234.
[11] Yuwana M, Seborg D E. A new method for on-line controller tuning [J]. AIChE, 1982, 28: 434-440.
[12] Jutan A, Rodriguez E. Extensions of a new method for on-line controller tuning [J]. Can J Chem Eng, 1984, 62: 802.
[13] Lee J. On-line PID controller tuning from a single closed-loop test [J]. AIChE J, 1989, 35: 329-331.
[14] Chen C L. a simple method for on-line identification and controller tuning [J]. AIChE J, 1989, 35: 2037-2039.
[15] Ziegler J G, Nichols N B. Optimum settings for automatic controllers [J]. Trans ASME, 1942, 64: 759-768.
[16] Lee J, Cho W, Edgar T. An improved technique for PID controller tuning from closed-loop tests [J]. AIChE J, 1990, 36: 1891-1895.
[17]  K J,
K J,  T. Automatic tuning of simple regulators with specifications on phase and amplitude margins [J]. Automatica, 1984, 20: 645-651.
T. Automatic tuning of simple regulators with specifications on phase and amplitude margins [J]. Automatica, 1984, 20: 645-651.
[18] Tyreus B, Luyben W. Tuning PI controllers for integrator/dead time processes [J]. Ind Eng Chem Res, 1992: 2625-2628.
[19] Haugen F. Comparing PI tuning methods in a real benchmark temperature control system [J]. Modeling, Identification and Control, 2010, 31: 79-91.
[20] Hu W, Xiao G. Analytical proportional-integral (PI) controller tuning using closed-loop setpoint response [J]. Ind Eng Chem Res, 2011: 2461-2466.
[21] Grimholt C, Skogestad S. Optimal PI control and verification of the SIMC tuning rule [C]// Proceedings of the IFAC Conference on Advances in PID Control PID’12. Brescia, Italy: IFAC, 2012.
[22] Skogestad S, Grimholt C. The SIMC method for smooth PID controller [C]// PID Control in the Third Millennium, Advances in Industrial Control. Springer, 2012: 147-175.
[23] Seki H, Shigemasa T. Retuning oscillatory PID control loops based on plant operation data [J]. Journal of Process Control, 2010, 20: 217-227.
[24] Veronesi M, Visioli A. Performance assessment and retuning of PID controllers for integral processes [J]. Journal of Process Control, 2010, 20: 261-269.
[25] Alcantara S, Vilanova R, Pedret C. PID control in terms of robustness/performance and servo/regulator trade-offs: A unifying approach to balanced autotuning [J]. Journal of Process Control, 2013, 23: 527-542.
[26] Alcantara S, Vilanova R, Pedret C, Skogestad S. A look into robustness/performance and servo/regulation issues in PI tuning [C]// Proceedings of the IFAC Conference on Advances in PID Control PID’12. Brescia, Italy: IFAC, 2012.
[27] Lee J, Cho W, Edgar T F. Simple analytic PID controller tuning rules revisited [J]. Industrial & Engineering Chemistry Research, 2013, 52: 12973-12992.
[28] Torrico B C, Cavalcante M U, Braga A P, Normey-Rico J E, Albuquerque A A. Simple tuning rules for dead-time compensation of stable, integrative, and unstable first-order dead-time processes [J]. Industrial & Engineering Chemistry Research, 2013, 52: 11646-11654.
[29] Shamsuzzoha M. A unified approach for proportional-integral-derivative controller design for time delay processes [J]. Korean Journal of Chemical Engineering, 2015, 32((4): 583-596.
[30] Shamsuzzoha M. Robust PID controller design for time delay processes with peak of maximum sensitivity criteria [J]. Journal of Central South University, 2014, 21(10): 3777-3786.
[31] Anwar M, Shamsuzzoha M, Pan S. A frequency domain PID controller design method using direct synthesis approach [J]. Arabian Journal for Science and Engineering, 2015, 40(4): 995-1004.
[32] Shamsuzzoha M, Skliar M, Lee M. PID control strategy for open-loop unstable processes with positive and negative zeros and time delay [J]. Asia-Pacific Journal of Chemical Engineering, 2012, 7: 93.
[33] Jin Q B, Liu Q. Analytical IMC-PID design in terms of performance/robustness trade-off for integrating processes: From 2-Dof to 1-Dof [J]. Journal of Process Control, 2014, 24(3): 22-32.
[34] Jeng J C, Tseng W L, Chiu M S. A one-step tuning method for PID controllers with robustness specification using plant step-response data [J]. Chemical Engineering Research and Design, 2014, 92(3): 545-558.
[35] Anil C, Sree R P. PID control of integrating systems using Multiple Dominant Poleplacement method [J]. Asia-Pacific Journal of Chemical Engineering, 2015, doi: 10.1002/apj.1911.
[36] Fu E P, Jeng J C. Closed-loop tuning of set-point-weighted proportional-integral-derivative controllers for stable, integrating, and unstable processes: a unified data-based method [J]. Industrial & Engineering Chemistry Research, 2015, 54(3): 1041-1058.
[37] Buckbee G. ExperTune Inc [EB/OL]. [2009] http://www.expertune.com.
[38] Visioli A. Practical PID control [M]. New York: Springer, 2006.
[39] Shamsuzzoha M. Closed-loop PI/PID controller tuning for stable and integrating process with time delay [J]. Ind Eng Chem Res, 2013, 52: 12973-12992.
[40] Chien I L, Fruehauf P. Consider IMC tuning to improve controller performance [J]. Chemical Engineering Progress, 1990, 86: 33-41.
[41] Luyben W. Identification and tuning of integrating processes with deadtime and inverse response [J]. Ind Eng Chem Res, 2003, 42: 3030-3035.
[42] Wang L, Cluett W. Tuning PID controllers for integrating processes [J]. IEEE Proceedings-CTA, 1997, 144: 385-388.
[43] Chen D, Seborg D. PI/PID controller design based on direct synthesis and disturbance rejection [J]. Industrial and Engineering Chemistry Research , 2002, 41: 4807-4822.
[44] Luyben W L. Plantwide dynamic simulators in chemical processing and control [M]. New York: Marcel Dekker, Inc, 2002.
(Edited by DENG Lü-xiang)
Received date: 2015-03-10; Accepted date: 2015-07-24
Corresponding author: Mohammad Shamsuzzoha; Tel: +966-13-860-7360; E-mail: mshams@kfupm.edu.sa, smzoha@gmail.com

