利用CFD模拟和ANN模型对A357铝合金大型复杂构件淬火槽内介质流场分布的优化设计
来源期刊:中国有色金属学报(英文版)2013年第5期
论文作者:杨夏炜 朱景川 何 东 来忠红 农智升 刘 勇
文章页码:1442 - 1451
关键词:A357铝合金;计算流体动力学;淬火槽;流速分布;人工神经网络
Key words:A357 aluminum alloy; computational fluid dynamics; quenching tank; flow distribution; artificial neural network
摘 要:基于计算流体动力学 (CFD) 的方法,建立具有两个搅拌系统和两个稳流装置的淬火槽模型,使用Fluent软件对槽内介质的流场分布进行模拟计算。采用文献中的淬火槽内介质流场模拟及实验验证了研究模型的有效性。为了综合考虑搅拌速度、定向流挡板的位置及槽内有效淬火区的位置等因素对介质流场的影响,采用CFD方法与人工神经网络 (ANN) 相结合的方法对淬火槽内流场的分布进行了研究。结果表明,人工神经网络预测的槽内介质流场大小与Fluent模拟结果非常吻合。这种淬火槽的优化设计方法,可对实际工业生产提供技术支持。
Abstract: Based on the computational fluid dynamics (CFD) method, a quenching tank with two agitator systems and two flow-equilibrating devices was selected to simulate flow distribution using Fluent software. A numerical example was used to testify the validity of the quenching tank model. In order to take tank parameters (agitation speed, position of directional flow baffle and coordinate position in quench zone) into account, an approach that combines the artificial neural network (ANN) with CFD method was developed to study the flow distribution in the quenching tank. The flow rate of the quenching medium shows a very good agreement between the ANN predicted results and the Fluent simulated data. Methods for the optimal design of the quenching tank can be used as technical support for industrial production.
Trans. Nonferrous Met. Soc. China 23(2013) 1442-1451
Xia-wei YANG1,2, Jing-chuan ZHU1,2, Dong HE1,2, Zhong-hong LAI1,2, Zhi-sheng NONG1,2, Yong LIU1,2
1. National Key Laboratory for Precision Hot Processing of Metals, Harbin Institute of Technology, Harbin 150001, China;
2. School of Materials Science and Engineering, Harbin Institute of Technology, Harbin 150001, China
Received 9 May 2012; accepted 4 August 2012
Abstract: Based on the computational fluid dynamics (CFD) method, a quenching tank with two agitator systems and two flow-equilibrating devices was selected to simulate flow distribution using Fluent software. A numerical example was used to testify the validity of the quenching tank model. In order to take tank parameters (agitation speed, position of directional flow baffle and coordinate position in quench zone) into account, an approach that combines the artificial neural network (ANN) with CFD method was developed to study the flow distribution in the quenching tank. The flow rate of the quenching medium shows a very good agreement between the ANN predicted results and the Fluent simulated data. Methods for the optimal design of the quenching tank can be used as technical support for industrial production.
Key words: A357 aluminum alloy; computational fluid dynamics; quenching tank; flow distribution; artificial neural network
1 Introduction
A357 (Al-7Si-0.6Mg) alloy is widely used in automotive industries, aerospace applications and other aspects because of its good corrosion resistance, excellent castability and high specific strength in the heat treated condition [1,2]. A357 alloy castings are used in the T6 condition (solution heat treatment, quenching and artificial aging). Quenching is one of the most important heat treatment processes in many industrial fields [3]. As for A357 alloy, the quick quenching can be helpful to inhibit the formation of Mg-Si precipitates [4]. But the inner stress and strain produced by quick cooling is the basic reason of distortion of the workpieces. Residual stresses occur for a variety of reasons, including inhomogeneous plastic deformations and heat treatment. It is known that residual stresses influence mechanical properties of material such as stress corrosion and fatigue life, and cause distortion and dimensional variation [5-7]. Many large complicated thin-wall parts are made using the conventional cast alloys A357. The solution treatment of A357 alloy large complicated thin-wall workpiece is determined by quenching medium and flow state of medium around workpiece [8]. In order to inhibit the formation of Mg-Si precipitates of large complicated thin-wall workpieces, the enough quenching speed of medium in the quenching tank must be provided. Enough quenching speed can be brought by agita tion of the quenching medium. But an increase in the quenching speed of medium will lead to large residual stresses for quenched parts. Therefore, it is very important to optimize the flow uniformity of quenching medium in the quenching zone and to predict the flow rate of quenching medium. Good control of quenching for A357 large complicated thin-wall workpieces will obtain better solution treatment effect and will be helpful to control the part distortion [9].
With the rapid development of computer technology, numerical simulation is used widely not only in academic institution to research the scientific issues of quenching but also in industrial production to solve the real engineering problems of quenching. The numerical simulation will help to reduce the cost of tests [10]. A numerical method of computational fluid dynamics (CFD) has been widely used for computing the flow rate and uniformity of quenching medium in quenching tank [11]. CFD can be used to solve the complex problems of fluid flow and predict the performance of fluid-thermal process that is often too difficult to solve with experimental or analytical techniques [12]. GARWOOD et al [13] used the CFD computer code and the experimental method to research the fluid flow in an agitated quenching tank. TOTTEN et al [14,15] reported the application of CFD modeling to illustrate the non-uniformity of quenching tank fluid flow. BOGH [16] used CFD method to research the effect of the placement of submerged spray eductors at different locations surrounding a rack of aluminum panel on quenching non-uniformity. HALVA and VOLNY [17] used CFD analysis to investigate the relationship between the homogeneity of fluid flow and agitator placement. Improvements in computational technologies enabled the researchers to use high fidelity CFD to study the flow distribution in a quenching tank. Every complete CFD analysis consists of three separate stages (modeling, CFD analysis and post-processing), and to complete these three stages will cost a great deal of time and effort. Optimization technique based on the artificial neural network (ANN) is beneficial for the researchers to reduce modeling and computation time by developing appropriate and high-accuracy ANN model. Recently, ANN has been widely applied to solving the problems of convection heat and flow processes [18-20].
In the previous studies, for a quenching tank with agitator systems and flow-equilibrating device, the effect of overall consideration of the two factors (agitation speed of impeller and position of directional flow baffle) on flow ability of quenching medium has not yet been reported. There are many different types of softwares, and they often use CFD method to model fluid flow, such as Fluent, CFX, Phoenics and Star-CD. In this study Fluent software was applied to simulating the flow rate and uniformity of quenching medium, and then a numerical example was used to testify the validity and the correctness of quenching tank model. Although CFD method is able to solve complex problems in many industrial fields, it is not suitable for use in optimal design. Therefore, the present study involves combining CFD analysis with ANN model to research the effect of the two parameters (agitation speed of impeller and position of directional flow baffle) on flow rate and uniformity of quenching medium in quenching tank. Based on the results simulated by Fluent software, an artificial neural network model with a back-propagation (BP) learning algorithm was developed to predict flow rate of quenching medium. Through the research of the effect of these two parameters (agitation speed of impeller and position of directional flow baffle) on flow rate and uniformity of quenching medium, we can evaluate how they impact on the flow uniformity. Finally, high accuracy network combined with the Fluent simulation instead of Fluent software, is applied to the optimization of quenching tank.
2 Computational fluid dynamics simulation
2.1 Governing equations of fluid flow
The basic conservation equations of mass, momentum and energy for incompressible flow problems can be expressed as [10]
Mass equation:  (1)
(1)
Momentum equation:
 (2)
(2)
Energy equation:
 (3)
(3)
where ρ is the fluid density; t stands for time; v is the fluid velocity vector; (px, py, pz) are Cartesian components of the stress tensor p; F is the body force vector per unit volume of a fluid particle; T is the thermodynamic temperature; cp is the specific heat capacity; k is the heat transfer coefficient of the fluid; S is a source of energy per unit volume per unit time.
2.2 Quenching tank
The quenching tank consists of two agitators, two impellers, two draft tubes, two overflow baffles and two directional flow baffles, as shown in Fig. 1(a). The quenching tank is rectangular with 2.5 m×2.5 m×3 m. The quenching zone is rectangular with 1 m×1 m×1 m. As can be seen in Fig. 1(a), the quenching tank has a vertical symmetry plane. The quenching tank has two vertical marine propellers that rotate in the same direction. Figure 1(b) shows three-dimensional model of A357 alloy large complicated thin-wall workpiece and it’s dimensions. In this work, an appropriate simplified model was created, which can reduce the difficulty of the mesh generation and save the computing time. The simplified model is shown in Fig. 2. Typically, impellers can be used as powerful agitation tools and the structural characteristics of impeller are diameter of 450 mm, number of blades 3 and pitch setting of 65 mm. Figure 3 shows the schematic of draft tube and flow baffle with dimensions.
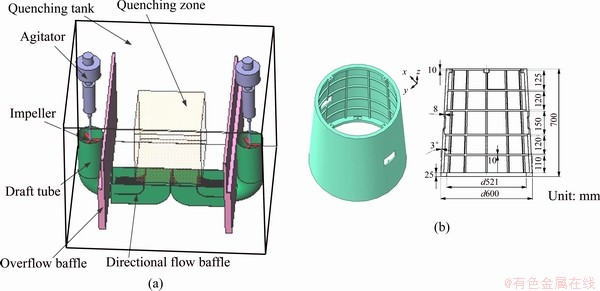
Fig. 1 Model of water quenching tank (a) and A357 alloy large complicated thin-wall workpiece (b)
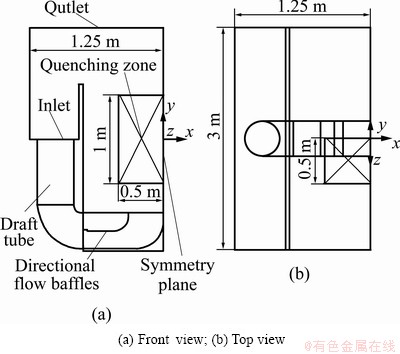
Fig. 2 Computational model of water quenching tank
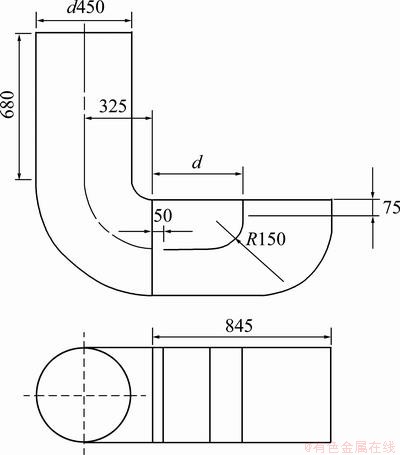
Fig. 3 Schematic of draft tube and flow baffle with dimensions (Unit: mm)
2.3 Numerical simulation method
The Fluent software is used to simulate liquid flow distribution in quenching tank. The Gambit software is an important tool to create the computational fluid dynamics (CFD) models. Tet/Hybrid elements, Tgrid type and interval size of 0.05 were selected for the quenching tank, which can get a good grid quality and the total nodes are 67926, and the total elements are 365666. Compared with quenching tank, the structure of draft tube is a complex and small part, so its mesh grid parameters were selected as follows: Tet/Hybrid elements, Tgrid type and interval size of 0.04 (total nodes 3573, total elements 16136). Figure 4 shows the mesh grid of simulation model.
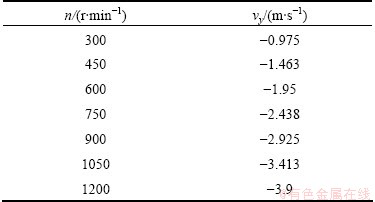
Water was selected as the quenching medium. The physical properties of water at 25 °C are as follows: density (ρ=997.04 kg/m3) and viscosity (m=8.904×10-4 Pa×s). The continuum hypothesis and the nonslip condition at the walls are applicable. In numerical simulation, the forward propulsion force of impeller agitation is only considered and the rotational force is ignored. The coordinate system is shown in Fig. 4. x-velocity (vx) and z-velocity (vz) of inlet are all zero. y-velocity (vy) of inlet can be calculated using the impeller parameters, including impeller diameter (d450), number of blades (N=3), pitch setting (p=65 mm) and rotational speed (n). Table 1 lists vy values at different impeller parameters. At the outlet, the pressure is set as one standard atmospheric pressure. Viscosity coefficient and density of water are set as constant.
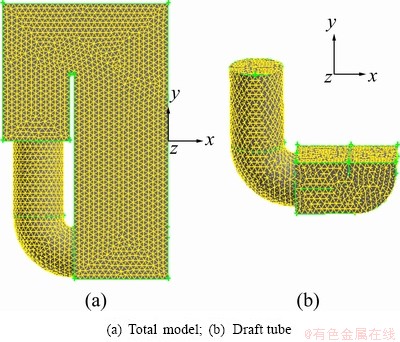
Fig. 4 Mesh diagram of quenching tank
Table 1 vy value at different impeller parameters
In this case, the flow is turbulent. The intense turbulence in the quenching tank can cause great loss of energy [21]. Turbulence model selection depends on many factors, such as quenching tank structure, accumulation of practical experience, the required accuracy and the availability of computational resources [22]. In the present work, standard k-epsilon turbulence model based on the Fluent software was selected for CFD simulation. It is a semi-empirical model based on the turbulent kinetic energy equation and the dissipation rate equation, which has been successfully used in many cases [23-25].
3 Neural network model
In this work, an artificial neural network (ANN) with a back-propagation (BP) learning algorithm was established to predict y-velocity of water flow in the quenching zone, a three-layered ANN architecture was developed and the number of neurons in the hidden layer was three. The agitation speed of impeller, the position of directional flow baffle and the coordinate position in quenching zone were used as the input variables, while y-velocity of coordinate position was taken as the output. Here the coordinate values were selected in such a way that y=0, z=0 and x=0-0.5 m. So, the x value was regarded as coordinate position in quenching zone and it is one of three input parameters. The datasets of ANN model obtained from Fluent simulation were divided into two sub-sets: a training set and a testing set. 75% of original datasets were selected as the training set; the remaining datasets were left for testing set. The inputs and outputs were normalized between 0.1 and 0.9 to ensure that all variables lie in the same range. In the output layer of the BP model, a linear function (purelin) was taken as the transfer function. The transfer functions in the hidden layers were sigmoid functions.
It is very important for ANN to decide how to train the network. Batch training was used in current work. In batch training, the weights and biases are only updated after all the inputs and targets are presented to the network. The use of mean square error (MSE) between Fluent simulation data and predicted values from the ANN is an excellent criterion for evaluating the performance of the network. The function of MSE can be expressed as
 (4)
(4)
where d(i) is the Fluent simulation value, a(i) is the predicted value from the ANN, and N is the number of data set.
The network training process was repeated many times by adjusting the parameters of network. Network with these characteristics provided good predictive performances: momentum rate of 0.6, learning rate of 0.1, MSE of 10-5 and the epochs of 10000. In addition, 8 neurons were used in hidden layer. The schematic diagram of BP network is shown in Fig. 5.
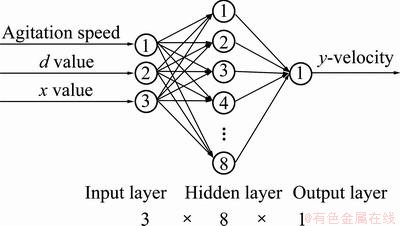
Fig. 5 Schematic diagram of BP artificial neural network
4 Results and discussion
4.1 Computational fluid dynamics results
Using the computational fluid dynamics (CFD) simulation method, the flow rate distributions in the quenching tank at 300, 600, 900 and 1200 r/min are obtained. Figure 6 illustrates the contours of velocities of water flow in the z=0 plane at different agitation speeds. It can be seen that, vortex phenomena were generated during mechanical agitation by impellers. As shown in Fig. 6(a), there are two vortexes (marked as region 2 and region 3) formed in the bottom of overflow baffle, other two vortexes (marked as region 1 and region 4) formed in the top of overflow baffle. Region 5 is the quenching zone of parts (Fig. 6(a)). The flow rate in quenching zone increases with agitation speed increasing. In Fig. 6, at the lowest agitation speed the vortex region is small (Figs. 6(a) and (b)), but becomes large with increasing impeller speed (Figs. 6(c) and (d)). Increasing the size of vortex region has adverse effects on the flow rate distribution in the quenching zone. Therefore, increasing the agitation speed can bring a large flow velocity in quenching zone, but it also increases the irregularity of water.
Figure 7 shows the y-velocity of water at the coordinate x of 0-0.5 m (y=0, z=0) in the quenching zone at different d values, where d is the position of directional flow baffle. It can be seen that the fluctuation of y-velocity of water increases as the agitation speed increases. The changing trends of velocity-position curves are dependent heavily on the position of directional flow baffle. Figure 7 indicates that the increase in d value has a little effect on the y-velocity of water flow in the quenching zone at low agitation speeds (≤450 r/min); when the agitation speed is above 450 r/min, the y-velocity values are found to be dependent heavily on agitation speed and d value. As shown in Figs. 7(b)-(d), with d value increasing, the flow uniformity of water in the quenching zone is significantly improved. But as shown in Figs. 7(d)-(f), with d value increasing, the flow uniformity of water in the quenching zone is worse.
4.2 Numerical example of computational fluid dynamics
In this study, a numerical example [26] was used to testify the validity and correctness of the quenching tank model. Structure of the quenching tank [26] was reproduced in Fig. 8. CHEN et al [26] used Ansys software to simulate flow distribution in quenching tank, while in the present study, Fluent software was carried out for numerical simulation. The present simulation results of a three-dimensional (3D) quenching tank model are compared with literature data, which are shown in Figs. 9 and 10. Compared with the simulation data in literature, the present simulation results show a higher accuracy in predicting the flow velocity of water in the quenching zone. In addition, the trends of flow velocity curves from the present simulation also coincide with the experimental curves in literature. After qualitative and quantitative analysis of the flow velocity curves, it can be concluded that the performance of the model of water quenching tank should be satisfactory and the simulation results are credible.

Fig. 6 Pathlines of flow velocities at different agitation speeds (z=0, d=300 mm)

Fig. 7 y-velocity of water in quenching zone(y=0, z=0, x=0-0.5 m)
4.3 Artificial neural network model results
In the above two parts, curves of y-velocity of fluid flow changes with the x value at different agitation speeds were obtained via CFD using Fluent software, the validity and correctness of the quenching tank model were testified by a numerical example. Here, the approach of Fluent simulation combined with ANN method was used to research the flow uniformity of water in the quenching zone.

Fig. 8 Structure of water quenching tank [26]

Fig. 9 Comparison of present simulation results and published literature data without directional flow baffles
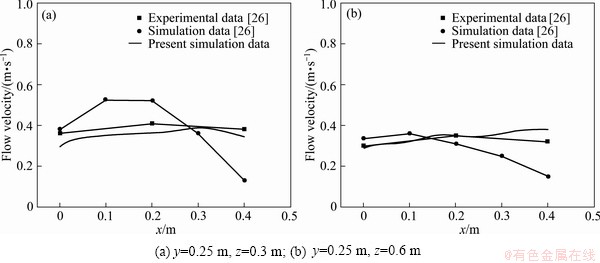
Fig. 10 Comparison of present simulation results and published literature data with directional flow baffles
The ANN model with the smallest predicted error is the result wanted. In the current studies, the correlation coefficient (R), average absolute relative error (eabr), and average absolute error (eab) were used to assess performance of the training and testing network, and the equations of R, eabr and eab can be described as follows:
 (5)
(5)
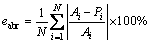 (6)
(6)
 (7)
(7)
where A is the actual value obtained from Fluent simulation; P is the predicted value from ANN model;  and
and  are the mean values of A and P values, respectively; N is the total number of desired data.
are the mean values of A and P values, respectively; N is the total number of desired data.
Figure 11 shows the comparison of ANN results with Fluent simulation data. As can be seen from Fig. 11, y-velocity shows good agreement between ANN results and Fluent results. Errors between y-velocity of Fluent software and ANN model are listed in Table 2. It can be seen from Table 2 that the y-velocity error between Fluent simulation and ANN model is very small. Therefore, the performance of the BP network is satisfactory.

Fig. 11 y-velocity obtained from Fluent simulation and ANN model (y=0, z=0, x=0-0.5 m)
Table 2 Error of ANN model for training and testing prediction

The correlation coefficient (R) was used to evaluate the closeness of fit of network architecture. Figure 12 indicates the closeness between predicted y-velocity from neural network and simulation data from Fluent. As can be seen from Fig. 12, the correlation coefficient is found to be 0.99986 and 0.99549 for training and testing data, respectively. The results show that the correlation coefficient is positive and close to 1, indicating that there is a strong positive linear relationship between ANN predicted data and Fluent simulation data. Therefore, the BP model can be employed effectively to model and predict the y-velocity of water in the quenching zone.
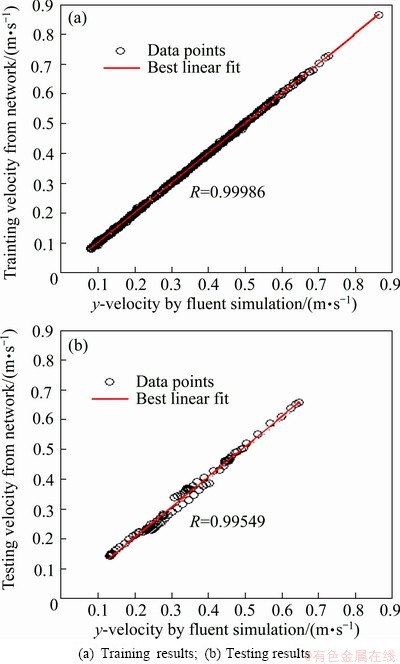
Fig. 12 Correlation between predicted data from neural network and Fluent simulation data
To summon up, the approach of ANN model co-design with CFD method is a very effective way to design the structure of the quenching tank, including the agitation speed, the position of directional flow baffle and the position of effective quenching zone.
5 Conclusions
1) Fluent CFD software was used to research the flow distribution of water in quenching tank. The results show that the agitation speed and the position of directional flow baffle have important impacts on the flow distribution and flow rate of water in quenching tank. Increasing the agitation speed can bring a large flow rate of water in quenching zone, but it also increases the irregularity of water, namely, the fluctuation of water flow velocity will increase.
2) The changing trends of velocity-position curves are dependent heavily on the position of directional flow baffle. By a numerical example, it is found that the simulation results from the present model are better than the simulation results in literature due to the fact that the present simulation results are more close to the experimental data.
3) Fluent simulation combined with ANN method enables solving the course of flow calculation to simplify greatly. The results show that the mean relative error between the predicted y-velocity of the ANN model and the experimental data is 4.24%, which demonstrates that the predicted ANN model has much higher precision and less error and the predicted values accord with the experiment data basically.
4) Flow rate and uniformity of quenching medium in quenching tank can be controlled using the approach of Fluent simulation combined with ANN method. Solution treatment and distortion of A357 aluminum alloy large complicated thin-wall workpieces can be adjusted by this approach. The highly successful combination of the Fluent simulation with ANN prediction model has been established which can not only provide an optimum design model for quenching system but also can be acceptable by usual engineering applications.
References
[1] ES-SAID O S, LEE D, PROST W D, GAMBERINI A, MESSIERI S. Alternative heat treatments for A357-T6 aluminum alloy [J]. Eng Fail Anal, 2002, 9(1): 99-107.
[2] Yang X W, ZHU JC, LAI Z H, KONG Y R, ZHAO R D, HE D. Application of artificial neural network to predict flow stress of as quenched A357 alloy [J]. Mater Sci Tech, 2012, 28(2): 151-155.
[3] Totten G E, Bates C E, Clinton N A. Handbook of quenchants and quenching technology [M]. Materials Park, OH: ASM International, 1993: 35-45.
[4] Callister W D. Materials science and engineering, an introduction [M]. USA, Hoboken: Wiley, 1994: 783-786.
[5] Eckersley J S, Meister T J. Intelligent design takes advantage of residual stresses [C]//Proc of the 3rd International Conference on Practical Applications of Residual Stress Technology. Ohio: ASM International, 1991: 175-181.
[6] Ruud C O. Residual stresses and their measurement, quenching and distortion control [C]//Proc of the First International Conference on Quenching and Control of Distortion. OH: ASM International, 1992: 193-198.
[7] Thakkar R, Shah R, Vanark V. Effects of hole making processes and surface conditioning on fatigue behavior of 6061-T6 aluminum [C]//Proc of SAE 2000 World Congress. Detroit: SAE International, 2000.
[8] Totten G E, Webster G M, Gopinath N. Quenching fundamentals: Effect of agitation [J]. Adv Mater Process, 1996, 149: 73-76.
[9] Tensi H M, Totten G E, Webster G M. Limitation of the use of grossman quench severity factors [C]//Proceedings of 17th heat treating society conference proceedings including the 1st international induction heat treating symposium. Ohio: ASM International, 1998: 423-431.
[10] Versteeg H K, Malalasekera W. An introduction to computational fluid dynamics: The finite volume method [M]. New Jersey: Prentice Hall, 1996: 45-65.
[11] Elkatatny I, Morsi Y, Blicblau A S, Das S, Doyle E D. Numerical analysis and experimental validation of high pressure gas quenching [J]. Int J Therm Sci, 2003, 42(4): 417-423.
[12] Baker A J. Potential for CFD in heat treating (computational fluid dynamics) [J]. Adv Mater Process, 1997, 10: 44-47.
[13] Garwood D R, Lucas J D, WALLIS R A, WARD J. Modeling of the flow distribution in an oil quench tank [J]. J Mater Eng Perform, 1992, 1(6): 781-787.
[14] Canale L C F, Totten G E. Quenching technology: A selected overview of the current state-of-the-art [J]. Materials Research, 2005, 8(4): 461-467.
[15] Totten G E, Bates C E, Clinton N A. Handbook of quenchants and quenching technology [M]. Ohio: ASM International, 1993: 339-411.
[16] Bogh N. Quench tank agitation design using flow modeling [C]// Heat Treating: Equipment and Processes: Conference Proceedings, Ohio: ASM International, 1994: 82-91.
[17] Halva J, Volny J. Modeling the flow in a quench bath [J]. Hutnicke Listy, 1993, 48(10): 30-34.
[18] Mahmoud M A, Ben-Nakhi A E. Neural networks analysis of free laminar convection heat transfer in a partitioned enclosure [J]. Commun Nonlinear Sci, 2007, 12(7): 1265-1276.
[19] OZUNAR A, ArcaklIoglu E, Nusret Dur F. The prediction of maximum temperature for single chips’ cooling using artificial neural networks [J]. Heat and Mass Transfer, 2009, 45(4): 443-450.
[20] VAROL Y, AVCI E, KOCA A, OZTOP H F. Prediction of flow fields and temperature distributions due to natural convection in a triangular enclosure using adaptive-network-based fuzzy inference system (ANFIS) and artificial neural network (ANN) [J]. Int Commun Heat Mass, 2007, 34(7): 887-896.
[21] HOU Q F, Zou Z S. Comparison between standard and renormalization group k-ε models in numerical simulation of swirling flow tundish [J]. ISIJ International, 2005, 45(3): 325-330.
[22]  Improvement of a chain-hardening furnace by computational fluid dynamics (CFD) simulation [J]. Applied Energy, 2005, 81(3): 260-276.
Improvement of a chain-hardening furnace by computational fluid dynamics (CFD) simulation [J]. Applied Energy, 2005, 81(3): 260-276.
[23] JHA P K, RANJAN R, MONDAL S S, DASH S K. Mixing in a tundish and a choice of turbulence model for its prediction [J]. Int J Numerical Methods Heat Fluid Flow, 2003, 13(8): 964-965.
[24] JHA P K, DASH S K, KUMAR S. Fluid flow and mixing in a six-strand billet caster tundish: A parametric study [J]. ISIJ International, 2001, 41(12): 1437-1439.
[25] FAN C M, SHIE R J, HWANG W S. Studies by mathematical and physical modelling of fluid flow and inclusion removal phenomena in slab tundish for casting stainless steel using various flow control device designs [J]. Ironmak Steelmak, 2003, 30(5): 341-342.
[26] CHEN N L, LIAO B, PAN J S, LI Q, GAO C Y. Improvement of the flow rate distribution in quench tank by measurement and computer simulation [J]. Mater Lett, 2006, 60(13-14): 1659-1664.
杨夏炜1,2, 朱景川1,2, 何 东1,2, 来忠红1,2, 农智升1,2, 刘 勇1,2
1. 哈尔滨工业大学 金属精密热加工国家级重点实验室,哈尔滨 150001;
2. 哈尔滨工业大学 材料科学与工程学院,哈尔滨 150001
摘 要:基于计算流体动力学 (CFD) 的方法,建立具有两个搅拌系统和两个稳流装置的淬火槽模型,使用Fluent软件对槽内介质的流场分布进行模拟计算。采用文献中的淬火槽内介质流场模拟及实验验证了研究模型的有效性。为了综合考虑搅拌速度、定向流挡板的位置及槽内有效淬火区的位置等因素对介质流场的影响,采用CFD方法与人工神经网络 (ANN) 相结合的方法对淬火槽内流场的分布进行了研究。结果表明,人工神经网络预测的槽内介质流场大小与Fluent模拟结果非常吻合。这种淬火槽的优化设计方法,可对实际工业生产提供技术支持。
关键词:A357铝合金;计算流体动力学;淬火槽;流速分布;人工神经网络
(Edited by Xiang-qun LI)
Corresponding author: Jing-chuan ZHU; Tel: +86-451-86413792; Fax: +86-451-86413922; E-mail: fgms@hit.edu.cn
DOI: 10.1016/S1003-6326(13)62615-1

