J. Cent. South Univ. (2018) 25: 1173-1181
DOI: https://doi.org/10.1007/s11771-018-3816-6
Dynamic model of saturator based on a global heat and mass transfer coefficient
HUANG Di(黄地)1, 2, ZHOU Deng-ji(周登极)1, ZHANG Hui-sheng(张会生)1,SU Ming(苏明)1, WENG Shi-lie(翁史烈)1
1. The Key Laboratory of Power Machinery and Engineering of Education Ministry,Shanghai Jiao Tong University, Shanghai 200240, China;
2. State Grid Jiangsu Electric Power Research Institute, Nanjing 211103, China
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2018
Abstract: Saturator is one of the core components of humid air turbine (HAT) and is the main feature of HAT making it different from other gas turbine cycles. Due to the lack of sufficient experience in commercial plant operation, HAT cycle has a great demand for modeling and simulation of the system and its components, especially the saturator, to provide reference for system design and optimization. The conventional saturator models are usually based on the theory of heat and mass transfer, which need two accurate coefficients to ensure convincing results. This work proposes a global heat and mass transfer coefficient based on cooling tower technology to model the saturator in small-scale HAT cycle. Compared with the experimental data, the simulation results show that the proposed model well predicts the dynamic humidity and temperature distribution characteristics of saturator at low air pressure and temperature.
Key words: saturator; cooling tower technology; global coefficient; dynamic modeling
Cite this article as: HUANG Di, ZHOU Deng-ji, ZHANG Hui-sheng, SU Ming, WENG Shi-lie. Dynamic model of saturator based on a global heat and mass transfer coefficient [J]. Journal of Central South University, 2018, 25(5): 1173–1181. DOI: https://doi.org/10.1007/s11771-018-3816-6.
1 Introduction
The humid air turbine (HAT) cycle, initially proposed by RAO [1], is one of the most advanced gas turbine cycles that is known for its high efficiency and low emission, as well as for its competitive cost, particularly in small and medium-capacity gas turbines [2]. Figure 1 shows the target efficiency of the HAT cycle system, along with that of existing gas turbine cycles [3]. Compared with conventional combined cycle, HAT cycle uses saturator instead of heat recovery steam generator (HRSG), leading not only to higher performance but also lower investment and less land occupation. The saturator, which acts as a pressurized humidification tower, permits the introduction of water under boiling point into the compressed air stream with minimal exergy losses.
Currently, there is only limited number of HAT plants and most of them are at test stage [4–8]. Therefore, the system simulation of HAT cycle plays a crucial role in its development. In particular, the problems such as the thermal property of humid air and humid gas [9], as well as the benefit from adding aftercooler [10], still need to be discussed further. More importantly, the saturator, which is the main difference from other gas turbine cycles, has a great demand for accurate and soluble modeling.
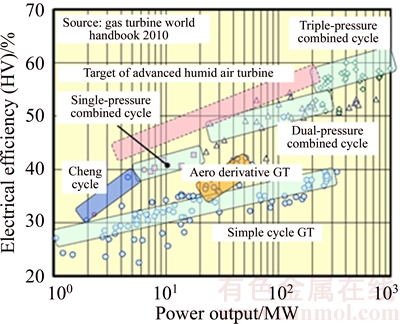
Figure 1 Target efficiency of HAT cycle system [3]
There has been a great amount of work done for the saturator process modeling in HAT cycle. Most of them are based on the theory of heat and mass transfer, in which the accuracies of the heat transfer coefficient and mass transfer coefficient play a significant role in modeling. WANG et al [11] used empirical formulas to calculate the coefficients. LIU et al [12] analyzed the relationship between two coefficients through the Lewis factor. CARATOZZOLO et al [13] used Bravo, Rocha and Fair correlations to evaluate the mass transfer coefficient. PAEPE et al [14] described the saturator as the heat and mass transfer among gas core, liquid film and dispersed droplets. However, these two coefficients (the heat transfer coefficient and the mass transfer coefficient) depend on many conditions so the exact values are not readily obtained especially during dynamic simulations. On the other hand, cooling tower (CT) technology is another kind of theory extensively discussed, which analyzes the heat and mass transfer together [15]. The theory has a good performance in low pressure saturator, thus can be used in small-scale HAT system. NYBERG et al [16] used pinch point of this theory for HAT cycle simulation, which could only solve the lumped steady-state model. PARENTE et al [17] integrated the cooling tower technology into steady model, using the number of transfer units (NTU) and the height of a transfer unit (HTU) to describe the humidification process. HUANG et al [18] utilized this model to analyze the HAT cycle based on the aeroderivative gas turbine. However, it was still focused on the steady-state simulation.
This work presents an improved non-iterative dynamic model for saturator.The cooling tower technology is utilized to build a novel model which can describe the heat and mass transfer process with one global coefficient. Then the distribution characteristics of humidity and temperature inside the saturator can be discussed through the proposed model. Simulation results of the model are consistent with the experimental data, showing that the mass transfer is not independent of the heat transfer for a well-designed saturator. The validation of the model shows that the global coefficient can well predict the humidification process of saturator.
2 Description of HAT cycle and saturator
Figure 2 shows a schematic diagram of the two-shaft arrangement of the typical HAT system, including an aftercooler, recuperator and economizer. The compressed air is cooled in the aftercooler and then sent to the saturator, where the heated water with more potential of evaporation is mixed with air and evaporated. The saturator increases the mass flow of humid air, leading to higher expansion work in turbine. The economizer recovers heat from the exhaust gas to the water, which also increases the potential of evaporation and provides more energy for the system. Furthermore, the intercooler and the water recovery system can also be integrated into the HAT system.
A real HAT system developed in Shanghai Jiao Tong University, which is based on basic layout without aftercooler and economizer, is shown in Figure 3 [19]. The saturator of this system is taken as the representative study object, which is designed as a packing saturator with the height of 0.8 m. The packing, increasing the heat and mass transfer area in a limited size, is described as many transfer units with the same height (HTU), in the model of CT technology.
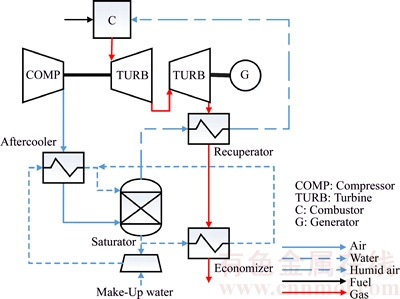
Figure 2 Schematic diagram of HAT system
Figure 3 HAT system of Shanghai Jiao Tong University [19]
3 A novel model for saturator based on cooling tower technology
3.1 Cooling tower technology
When using the cooling tower technology, a straight operating line, which can be defined by the following equation, is considered in the temperature–enthalpy diagram [17],
where h′ stands for specific enthalpy per dry air and T stands for temperature; The subscripts (a,in), (a,out) and (w,in), (w,out) denote air inlet/outlet and water inlet/outlet conditions, respectively; The term Δhs,max represents the maximum enthalpy difference within the interval [Tw,1, Tw,2], between the saturation curve and the line with a slope α (parallel to the operating line) that passes through the origin of the axes (Figure 4). On the other hand, the saturation curve, which is defined as the saturated enthalpy at temperature of water, is always at the top of operating line to guarantee saturating potential. The term Δhpp at the enthalpy pinch point, is the minimum enthalpy difference between the operating line and the saturation curve for the required thermodynamic evolution. Note that the specific enthalpy and humidity of humid air are both based on the mass of dry air, thus that the units are kJ/kgdry and kg/kgdry, respectively.
Because both the heat transfer and mass transfer are related to the enthalpy difference between the saturation curve and operating line, a global (heat and mass) transfer coefficient is proposed (kG). The enthalpy balance and mass transfer equation can be written as [17],
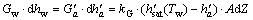(1)
where G, A and Z stand for the mass flow rate, interface water/air as well as the height of saturator, respectively; h′sat is the saturated enthalpy and h′a is the real enthalpy, which are corresponding to the two lines in Figure 4. Rearranging the terms in Eq. (1) and integrating between h′a,in and h′a,out, it can be written as [17],
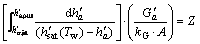(2)
This is the Merkel equation in which the first term in brackets represents the number of transfer units (NTU) and the second term is the height of a transfer unit (HTU).
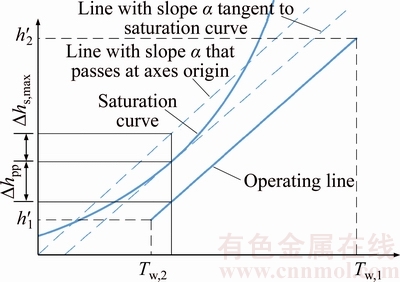
Figure 4 Temperature–enthalpy diagram [16, 17]
3.2 Dynamic model for saturator
With a global transfer coefficient, the NTU and the HTU proposed, the modeling of the saturator can be simplified. The existing work [13, 14] only provides a steady model which needs iteration of outlet temperature of water. In this paper, an improved non-iterative dynamic model is proposed.
To build a new dynamic model based on CT theory, the following assumptions are made to describe the dynamic behaviors of the heat and mass transfer,
1) The heat and mass transfer shares one global coefficient. That is to say, the mass transfer is not independent of heat transfer. In addition, when considering the dynamic response of humidification process, the heat and mass transfer processes are assumed to get stable in the same time.
2) There is no difference for temperature and humidity along radial direction. That is to say, the temperature and humidity of the humid air in the saturator will change only along the axial direction.
3) The pressure and mass flow characteristics is not concerned in this paper, which means that the mass flow rate is only related to the evaporation. There is no pressure change caused by volume inertia.
Based on the control volume method and conservation theorem, the dynamic model for saturator can be obtained as follows:
Conservation of mass,
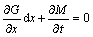(3)
Conservation of energy,
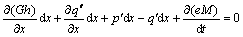(4)
It is difficult to solve the above partial differential equations thus cannot meet the requirements for system dynamic simulation. The Leibniz’s law and divergence theorem are used to convert the above partial differential equations into ordinary differential equations. The module modeling method is employed and the saturator is divided into 10 compartments. Figure 5 shows the heat and mass transfer in a compartment.
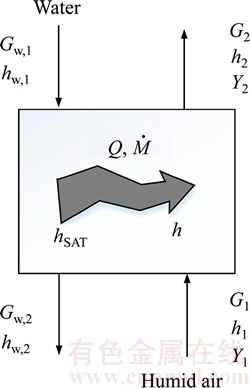
Figure 5 Heat and mass transfer in a compartment of saturator
In Figure 5,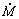 
is the mass transfer and Q is the heat transfer, both related to the enthalpy difference as mentioned above; Y stands for the absolute humidity of air.
After dividing the whole saturator into several compartments, we can get the state equations for each compartment,
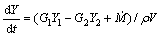(5)
where ρ is the density of air and V is the volume of compartment.
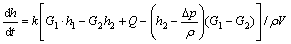(6)
where k is the adiabatic coefficient and p is the pressure of air.
Based on the cooling tower theory, the relationship between them can be written as
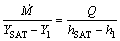(7)
where YSAT is the absolute humidity and hSAT is the enthalpy of saturated humid air at the temperature of water, corresponding to the saturation curve in Figure 4.
Because both the HTU and NTU are steady-state parameters, a new coefficient to describe the dynamic process is needed. Thus, the global transfer coefficient kG is converted into a new parameter for dynamic model, which refers to the traditional heat transfer theory,
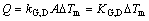(8)
where KG,D is the new global dynamic coefficient considering the heat and mass transfer rate as well as the transfer area. Thus, we can calculate the heat transfer and mass transfer in each compartment.
The saturator is split into 10 compartments named as 1, 2, …, 10, respectively, along the direction of humid air flow. So, all the parameters can be written as X (i, j), where i stands for the compartment and j stands for the simulation step.
With the state equation built, the new state values of the next step can be calculated as
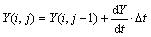(9)
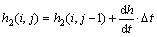(10)
where Δt is the simulation step.
As mentioned before, the volume inertia is not considered in this paper. So, the output mass flow rate is only related to the evaporation.
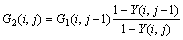(11)
The inlet mass flow rate of each compartment can be written in the following equations because of the counter flow of humid air and water. The enthalpy and humidity have the same equations:
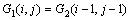(12)
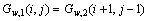(13)
In summary, the relationship between heat transfer and mass transfer is based on the cooling tower technology, which is related to the enthalpy difference between saturated air and real humid air. The heat transfer can be calculated using traditional method, while the transfer coefficient represents both heat transfer and mass transfer.
4 Experiment, simulation and results
The experiments are implemented with the saturator in Shanghai Jiao Tong University. There are 24 groups of experiments with different inlet pressures, temperatures and mass flow rates of air, as well as different inlet temperatures and mass flow rates of water. The air is directly from the compressor of HAT cycle test system of Shanghai Jiao Tong University, thus the pressures, temperatures and mass flow rates are related. The temperatures of water are set as 333, 343, 353 and 363 K. Moreover, various mass flow rates of water are chosen for the various conditions of air, in order to ensure the air/water mass flow rate ratio to be 2 or 1.
4.1 Steady state
The experiments are divided into 6 cases. Each case has the same inlet air parameters and same air/water ratio, while has 4 different inlet temperatures of water. Table 1 shows the inlet pressure, temperature and mass flow rate of dry air, as well as the mass flow rate of water of each group.
Table 1 Experimental conditions
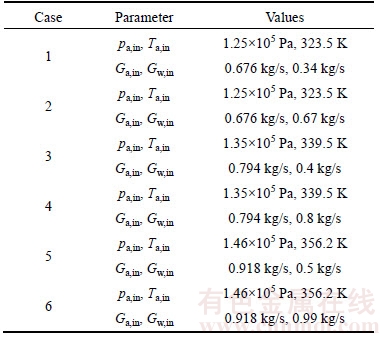
For different experimental conditions, the different HTUs should be assumed. However, with the same inlet air parameters and the same air/water ratio in each case, the property of heat and mass transfer is similar thus we can assume that the HTU is constant in each case to simplify the simulation condition, especially at low pressure and temperature. Table 2 shows the HTU, relative error of humidity as well as relative error of outlet water temperature of each case. Although the maximum error of 6.067% occurs in Case 2 with water temperature 363 K, the absolute error is only 0.0054 kg/kgdry. So, the accuracy of the simulation is acceptable with constant HTU in each case.
The simulation results of humidity and outlet water temperature at steady-state are shown in details in Figures 6 and 7, respectively, and are compared with the experimental data. The solid lines (E) represent the measured experimental data while the dashed lines (S) represent the simulation results. The figures show that the average absolute error is 0.00127 kg/kgdry and the average relative error is 2.075%. Furthermore, the average absolute error of outlet temperature of humid air is only 1.958 K, while the relative error is extremely small in Kelvin degree. Although using variable HTU in each case can improve the performance of the model, the model becomes complicated and the parameters for dynamic simulation are difficult to obtain. From the above analysis, it can be seen that using constant HTU can meet the requirement of accuracy thus the simplified steady model is utilized in order to get a constant global coefficient for the following dynamic simulation.
Table 2 HTU of each case
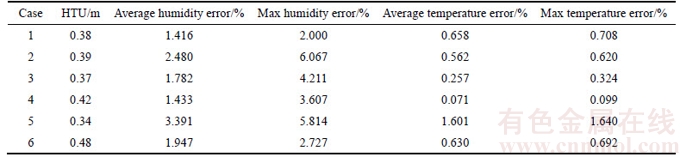
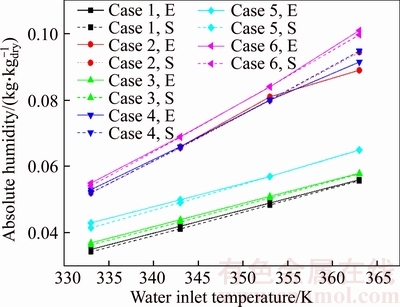
Figure 6 Simulation results of humidity of air: (E: experimental data; S: Simulation result)
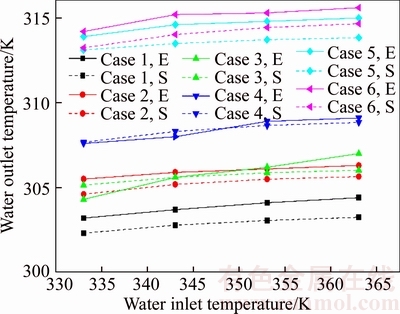
Figure 7 Simulation result of outlet temperature of water: (E: Experimental data; S: Simulation result)
Once the global coefficient is assumed as a constant in each case, distribution characteristics can be solved from the steady-state. Figure 8 shows the NTU distribution when the inlet temperature of water is 373 K for Case 1. The saturation curve and operating line are corresponding to the two lines in Figure 4, while the bars stand for the NTU in each compartment in the saturator. The enthalpy difference is larger at the inlet of water, which results in low NTU to transfer heat and mass. This is to say that smaller size is needed to transfer heat and mass.
Figure 8 NTU distribution
The temperature of water and humidity of air distributions in the saturator are shown in Figure 9. Notice that the x-axis is the height of saturator, which means that this figure shows the distributions along the physical structure. Due to the NTU distribution caused by changing enthalpy difference, the heat and mass transfer is faster at the inlet of water. Therefore, change rates of both temperature and humidity are larger at the top of saturator.
Figure 9 Temperature of water and absolute humidity of air distribution
4.2 Dynamic simulation
In this work, we focus on the humidity distribution, so the dynamic simulation is based on the process from dry condition to the fully saturated condition. The experiment of Case 1 with inlet water temperature 333 K is chosen as the simulation object. As mentioned above, the saturator is divided into 10 compartments. The dynamic global coefficients are calculated by the results of steady-state analysis and Eqs. (5) and (6), when dY/dt=0 and dh/dt=0, which are listed in Table 3. The height and volume of each compartment are not equal, due to the result of NTU distribution.
Table 3 Dynamic simulation conditions
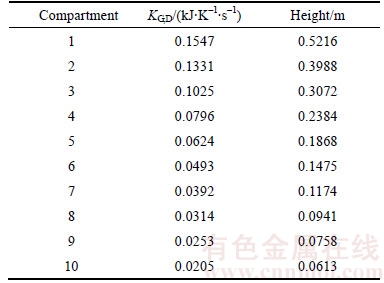
Figure 10 shows the dynamic response of output humidity of humid air and outlet temperature of water. The saturator begins to work at the 10th. It takes about 40 s for humidity to achieve stability, which is faster than outlet temperature. It is because the thermal inertia of air is smaller than water, and is also because outlet humidity is mainly related to the constant inlet temperature of water. In fact, the humidity is still decreasing with the output temperature, but the quantity is much smaller.
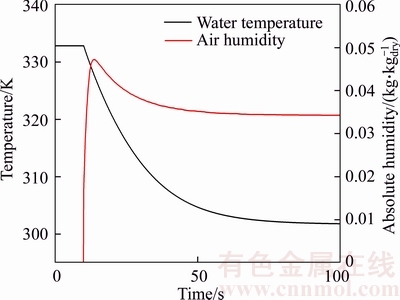
Figure 10 Humidity and temperature dynamic response
The final humidity after achieving stability is 0.0343 kg/kgdry, which is very close to the result of steady-state simulation, with the absolute error only 0.0007 kg/kgdry from the experimental result. The final outlet temperature is 301.737 K. The absolute error is 1.613 K.
The humidity distribution varies with heat and mass transfer. As shown in Figure 10, the outlet humidity changes faster in the first 5 s, thus the humidity distribution response in the 5 s is drawn in Figure 11. The x-axis represents the height of saturated and the five lines show the humidity distributions at different time. The outlet humidity changes faster in this period of time and air becomes over-humidified. It is because the enthalpy difference between saturated condition and real humid air is large during this period of time. The humidity at the inlet of air does not change a lot due to the low heat transfer caused by low temperature difference.
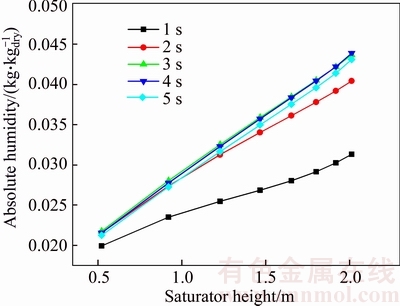
Figure 11 Humidity distribution dynamic response in 5s
Figure 12 depicts the dynamic response from the 5th second to the 30th second with an interval of 5 s. The humidity continues decreasing because the air has been over-humidified. The humidity distribution characteristics do not change a lot during this period of time, until the humidity achieves stability.
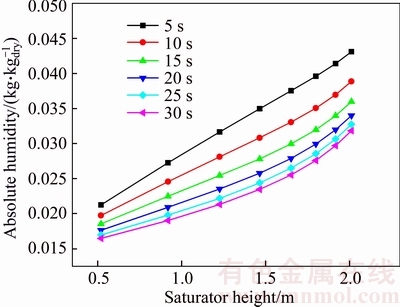
Figure 12 Humidity distribution dynamic response in 30s
In summary, the 24 groups of experiments are divided into 6 cases. When the HTU of each case is assumed to be constant, the simulation results of steady state are acceptable with the maximum humidity error 0.0054 kg/kgdry. Then the dynamic simulation from the dry condition to the fully saturated condition is done.The dynamic responses show that the air would be over-humidified at the beginning of the humidification process and then drop. The simulation results after achieving stability are compared with the experimental data with the relative error only 2%.
5 Conclusions
The model for saturator based on a global heat and mass transfer coefficient has been proposed in this paper. An assumed height of transfer unit (HTU) is employed to calculate the humidity and enthalpy distribution characteristics under steady state. The dynamic global coefficient and height of each compartment of saturator are obtained from the steady-state simulation results. Compared with the traditional model using two coefficients to describe the humidification process, the proposed model reduces the number of simulation conditions, thus the conditions are easier to be obtained and the simulations are more feasible. Although the model is simplified, simulation results are still consistent with the experimental data. The following conclusions can be drawn,
1) The cooling tower technology can be used in the simulation of saturator. It meets the requirements for not only steady state but also dynamic simulation.
2) The height of transfer unit (HTU) is chosen as the simulation condition for steady-state, which is mainly related to the parameters of air as well as the air/water mass flow ratio. The dynamic global heat and mass transfer coefficient and height of compartment are the conditions for dynamic simulation.
3) The proposed model simplified the heat and mass transfer, using a single global coefficient to describe the process of transfer. The new coefficient can well predict the dynamic characteristics of saturator at low air pressure and temperature.
4) The modeling method of the proposed model is focused on the low pressure saturator, so it can be used in the small-scale humid air turbine (HAT) system simulation.
In summary, the proposed model solves the problem that the traditional heat transfer coefficient and mass transfer coefficient not readily obtained especially during off-design and dynamic simulations. The simplified model based on the global heat and mass transfer coefficient can well predict the humidification process of low pressure saturator and can be used in small-scale HAT cycle system.
Variables
A Area
G Mass flow rate
h Enthalpy
k Coefficient
K Coefficient considering area
M Mass
Q Heat
T Temperature
t Time
V Volume
Y Absolute humidity
Z Height
ρ Density
Subscripts
a Air
d Dynamic
g Global
pp Pinch point
s Saturation curve
sat Saturated air
w Water
References
[1] RAO A D. Process for producing power: US, US4829763 [P]. 1989–05–16.
[2] NAKHAMKIN M, PELINI R, PATEL M I, WOLK R. Power augmentation of heavy duty and two-shaft small and medium capacity combustion turbines with application of humid air injection and dry air injection technologies [C]// ASME 2004 Power Conference. Baltimore, 2004: 301–306.
[3] FARMER R. Gas turbine world handbook [M]. Fairfield: Gas Turbine World, 2010.
[4] AGREN N D, WESTERMARK M O, BARTLETT M A, LINDQUIST T. First experiments on an evaporative gas turbine pilot power plant: Water circuit chemistry and humidification evaluation [J]. Journal of Engineering for Gas Turbines and Power-Transactions of the ASME, 2002, 124(1): 96–102.
[5] HATAMIYA S, ARAKI H, HIGUCHI S. An evaluation of advanced humid air turbine system with water recovery [C]// ASME Turbo Expo 2004: Power for Land, Sea, and Air. Vienna, 2004, 7: 585–591.
[6] KUROKI H, HATAMIYA S, SHIBATA T, KOGANEZAWA T, KIZUKA N, MARUSAIMA S. Development of elemental technologies for advanced humid air turbine system [J]. Journal of Engineering for Gas Turbines and Power-Transactions of the ASME, 2008, 130(3): 183–189.
[7] ARAKI H, IWAI Y, TAKEDA T, MORISAKI T, SATO K. Test results of 40MW-class advanced humid air turbine and exhaust gas water recovery system [C]// ASME Turbo Expo 2014: Turbine Technical Conference and Exposition. Düsseldorf, 2014, 3A.
[8] de PAEPE W, CARRERO M M, BRAM S, CONTINO F. T100 micro gas turbine converted to full humid air operation: test rig evaluation [C]// ASME Turbo Expo 2014: Turbine Technical Conference and Exposition. Düsseldorf, 2014, 3A.
[9] WANG Zi-dong, CHEN Han-ping, WENG Shi-lie. New calculation method for thermodynamic properties of humid air in humid air turbine cycle—The general model and solutions for saturated humid air [J]. Energy, 2013, 58(5): 606–616.
[10] WANG Bo, ZHANG Shi-jie, XIAO Yun-han, XU Zhen. A comparison of the hat (humid air turbine) cycle performance of a micro gas turbine with and without an aftercooler [J]. Journal of Engineering for Thermal Energy & Power, 2010, 25(1): 39–42. (in Chinese)
[11] WANG Yu-zhang, LI Yi-xing, WENG Shi-lie, WANG Yong-hong. Numerical simulation of counter-flow spray saturator for humid air turbine cycle [J]. Energy, 2007, 32(5): 852–860.
[12] LIU Chun-qi, SONG Hua-fen. Lewis factor and its impact on simulation of saturator [J]. Gas Turbine Technology, 2008, 21(1): 50–53. (in Chinese)
[13] CARATOZZOLO F, TRAVERSO A, MASSARDO A F. Implementation and experimental validation of a modeling tool for humid air turbine saturators [J]. Applied Thermal Engineering, 2011, 31(16): 3580–3587.
[14] de PAEPE W, CONTINO F, DELATTIN F, et al. New concept of spray saturation tower for micro Humid Air Turbine applications [J]. Applied Energy, 2014, 130: 723–737.
[15] TREYBAL R E. Mass-transfer operation[M]. Columbus: McGraw-Hill, 1968.
[16] NYBERG B, THERN M. Thermodynamic studies of a HAT cycle and its components [J]. Applied Energy, 2012, 89(1): 315–321.
[17] PARENTE J O S, TRAVERSO A, MASSARDO A F. Saturator analysis for an evaporative gas turbine cycle [J]. Applied Thermal Engineering, 2003, 23(10): 1275–1293.
[18] HUANG Di, CHEN Jin-wei, ZHOU Deng-ji, ZHANG Hui-sheng, SU Ming. Simulation and analysis of humid air turbine cycle based on aeroderivative three-shaft gas turbine [J]. Journal of Central South University, 2018, 25(3): 662–670.
[19] WEI Chen-yu, ZANG Shu-sheng. Experimental investigation on the off-design performance of a small-sized humid air turbine cycle [J]. Applied Thermal Engineering, 2013, 51(1, 2): 166–176.
(Edited by YANG Hua)
中文导读
一种基于通用传热传质系统的新型饱和器的动态建模方法
摘要：饱和器是湿空气透平（HAT）循环最重要的部件之一，也是HAT循环与其他燃气轮机循环最重要的区别。由于缺少相关商业运行的经验，热力系统建模与仿真，特别是对饱和器的建模、仿真工作，对HAT循环系统设计、优化有着至关重要的意义。传统饱和器模型通常是基于传热传质理论，该理论需要精确的传热系数和传质系数来保证模型的准确性。本文提出了一种利用基于冷却塔模型的通用传热传质系数来描述小型HAT循环系统中饱和器的建模方法。通过与仿真结果的比较表明，该模型可以很好地预测饱和器在低压低温条件下的内部湿度和温度的动态分布特性。
关键词：饱和器；冷却塔模型；通用系数；动态建模
Foundation item: Project(2017YFB0903300) supported by National Key R&D Program of China; Project(2016M601593) supported by China Postdoctoral Science Foundation
Received date: 2016-04-20; Accepted date: 2016-09-26
Corresponding author: ZHANG Hui-sheng, PhD, Professor; Tel: +86–13818875114; E-mail: zhslm@sjtu.edu.cn; ORCID: 0000-0002- 4771-3986
