桩基悬臂式挡墙组合结构设计理论研究
谢康1, 2，周珩2，张乐2，陈晓斌1，苏谦2，王业顺1
(1. 中南大学 土木工程学院，湖南 长沙，410075；
2. 西南交通大学 土木工程学院，四川 成都，610031)
摘要：结合桩基悬臂式挡土墙的受力状态和变形模式，提出桩基悬臂式挡土墙的设计理论以及特殊工况条件下稳定性检算内容和计算方法，选取典型工点，验证设计理论的合理性。研究结果表明：提出桩基悬臂式挡土墙结构设计的高宽比为1.6~2.0，横向桩间距为3~4倍桩径，纵向桩间距为3~5倍桩径；悬臂段后填土为黏性土采用库仑理论计算土压力，砂性土则采用郎金理论计算土压力；基于现场实测发现桩基悬臂式挡墙内力测试结果与理论计算结果类似，结构稳定性检算通过，可见双排桩基悬臂式挡土墙起到了较好的控制路基水平变形的作用。
关键词：桩基悬臂式挡墙；设计理论；受力特性；原位试验
中图分类号：U213 文献标志码：A
文章编号：1672-7207（2021）07-2349-11
Theoretical research on design of combined structure of cantilever retaining wall of pile foundation
XIE Kang1, 2, ZHOU Heng2, ZHANG Le2, CHEN Xiaobin1, SU Qian2, WANG Yeshun1
(1. School of Civil Engineering, Central South University , Changsha 410075, China;
2. School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China)
Abstract: Combined with the stress state and deformation mode of pile foundation cantilever retaining wall, the design theory of pile foundation cantilever retaining wall was put forward. Typical field test was selected to verify the rationality of the design theory. The results show that the recommended value of height width ratio is 1.6-2.0, the recommended value of transverse pile spacing is 3-4 times of pile diameter, and the recommended value of longitudinal pile spacing is 3-5 times of pile diameter; the filling behind the cantilever section is cohesive soil, and the Coulomb theory is used to calculate the earth pressure, while the Rankine theory is used to calculate the earth pressure for sandy soil.
Key words: pile foundation cantilever retaining wall; design theory; mechanical characteristics; field test
山区铁路在修筑过程中，往往会碰到高填方路基及陡坡路堤，轻型支挡结构因其造价低、可因地制宜的优点而受到广泛推广[1]。我国山区普遍具有复杂的地形地貌，地质条件也不尽相同，其对新型支挡的设计和施工要求愈来愈高，同时工程上正面临着诸多难题[2]：难以分析结构的受力机理、确定设计参数等等。为了满足这种需求、解决相关难题，亟需提出一种适用于复杂山区陡坡路堤、直立收坡的新型支挡结构。目前，重力式挡土墙、加筋土挡土墙、悬臂式挡土墙、土钉墙板式挡土墙、短卸荷板式挡土墙、预应力锚索和抗滑桩等在路基边坡工程中被广泛应用[3-8]。其中，作为轻型支挡结构物的悬臂式和扶壁式挡土墙因具有良好的外观形式、挡土高度较高、质量轻、厚度小，同时造价较低，对地基承载力的要求也不高等优点，近年来挡土墙在铁路、公路等项目中应用越来越广泛[9]。
在实际工程中，很多情况下为了凸显挡土墙的优越性可以适当地对悬臂式、扶壁式挡土墙做改进[10-12]。桩基础悬臂式、扶壁式挡土墙实质上是“挡土部分为悬臂式挡土墙，基础部分采用钢筋混凝土钻孔灌注桩或打入桩等[13]”的一种新型支挡结构形式。其以桩基作为挡土墙结构的基础，解决了一般悬臂式挡土墙必须依靠增大基础尺寸来提供抗倾覆滑移反力和减小地基承载力的问题，进而能够减小挖方段的开挖量。桩基础处理能够提供较高的竖向地基承载力。因此采用支挡体系的挡土墙与桩基础结合，可使挡土墙的适用范围扩大一步。设计中挡土墙的基底应力、抗倾覆稳定性及抗滑稳定性等结构特性不再由底板尺寸和基底土特性决定，而是由桩基础来支撑挡土墙并抵抗挡土墙的倾覆及滑动。目前桩基悬臂式挡墙的研究多在于理论计算和数值模拟：任庆昌[14]对底板受力和力学分析方法、基础桩的内力和变为分析方法以及底板抗冲切的计算方法进行了深入探讨；姚裕春等[13]开展双排桩基悬臂式挡土墙的结构参数影响分析，对桩基悬臂式挡墙设计得出了几点重要结论：1) 双排桩基横向排间距宜为3~4倍桩径或桩宽，且不宜超过6 m；2) 双排桩基上部悬臂式挡土墙的悬臂高度应保持在1.6~2.0倍的底板宽度内；3) 桩基的受力和结构变形对悬臂式挡土墙底板厚度并不敏感，但是过大的板厚不利于结构安全；周珩等[15-16]则对桩基悬臂式挡墙的受力机理进行了数值计算以及参数分析，并且研究了在软土地基中桩基悬臂式挡墙的应用，着重对踵板长度、锚固深度、排间距和土体弹性模量对结构变形、内力的影响进行了分析，同时提出了建议：1.6~2.0是结构设计高宽比的合适范围，并根据线路的变形控制指标与地基情况采取合适的软土加固措施；刘杰[17]则结合数值模拟，通过整体考虑各因素对结构的影响，进而优化了设计参数，得出较合理的结果。
前人对于桩基悬臂式挡墙多在于其计算理论和结构选型分析，而系统化针对桩基悬臂式挡墙设计检算成套理论鲜有涉及，且缺少现场试验的验证。故本文作者结合双排桩基悬臂式挡土墙的受力状态和变形模式，通过系统分析，提出双排桩基悬臂式挡土墙的设计理论以及特殊工况条件下稳定性检算方法，最后选取典型工点，验证设计理论的准确性，并对其安全性深入分析，进而为桩基础悬臂式挡土墙的工程应用推广提供理论基础。
1 桩基悬臂式挡墙组合结构设计思路
1.1 组合支挡结构承载机理
双排桩基悬臂式挡土墙实质上是“挡土墙部分为悬臂式挡土墙，基础部分采用双排钢筋混凝土钻孔灌注桩、挖孔桩或打入桩等”的一种新型支挡结构形式，其综合了悬臂式挡土墙与桩基托梁结构的技术特点，其特征在于由上部的挡土墙结构、下部的钢筋混凝土桩基与填土组成联合支挡结构。一方面，桩基础的运用不仅解决了一般性挡土墙地基承载力不足、抗滑移能力不足、抗倾覆能力不足等问题，而且增强了结构的整体刚度与抗变形能力；另一方面，类似托梁结构的存在可以与桩体形成连续的刚架型结构，既可以减小填土对桩基的水平推力作用，又可以将上部填土的竖向荷载传递给地基与桩基础，结构如图1所示。
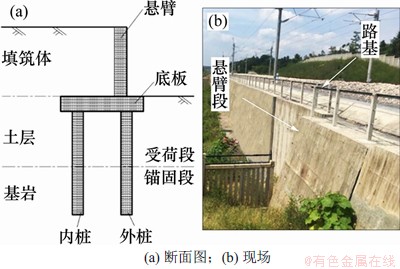
图1 桩基悬臂式挡土墙
Fig. 1 Pile foundation cantilever retaining wall
1.2 组合支挡结构设计流程
由于组合结构沿线路纵向结构与受力对称，故可将各排构件投影于外力作用平面来分析与计算(纵向取单跨宽度计算)。
由于桩基悬臂式挡土墙结构底板为整体结构中传递荷载与协调变形的重要组成部分，其受力相对复杂，结构设计时会通过增加底板厚度或刚度以保证整体结构的安全与稳定，故在空间框架结构的设计计算时可视底板为相对刚体。忽略底板下侧地基摩擦力和地基反力的作用，桩基设计荷载即为挡土墙底板传递至桩基中各桩桩顶的轴向力、剪力和弯矩，以及桩基与周围岩土体的相互作用力。通过将单桩分解为受荷段与锚固段分别受力分析，再考虑力系平衡与结构协调变形等条件，推导空间框架结构的内力计算公式。
本文提出双排桩基悬臂式挡土墙设计由结构截面尺寸拟定和钢筋混凝土结构设计组成。通过试算法确定结构各部件的断面尺寸，具体是先拟定挡土墙部分截面的试算尺寸，然后计算其承受的土压力，并全部进行稳定性验算，最终确定踵板的宽度以及桩基的尺寸，结构设计流程如图2所示。
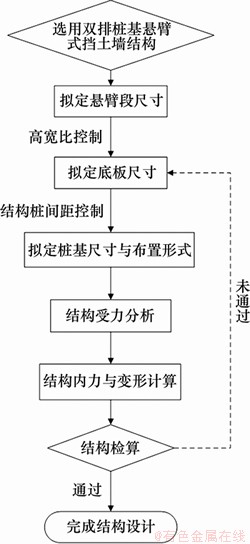
图2 桩基悬臂式挡土墙结构设计流程
Fig. 2 Structural design process of pile foundation cantilever retaining wall
2 桩基悬臂式挡墙组合体系设计方法
2.1 结构关键参数分析
基于桩基悬臂式挡土墙计算理论[16]，编写了双排桩基悬臂式挡土墙计算程序。根据该结构的结构形式与受力变形特征可知，挡土墙高度与踵板宽度之比(以下简称高宽比)、桩间距以及地基土参数等为关键设计参数[18]。因此通过建立结构模型，以单一变量原则对高宽比、桩间距等参数进行参数敏感性分析，计算模型如图3所示。图3中，BL为横向桩间距，BL′为纵向桩间距。
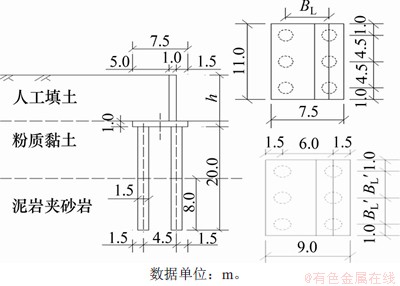
图3 计算模型图
Fig. 3 Calculation model diagram
2.1.1 高宽比计算分析
高宽比直接影响结构的受力与变形：当高宽比过大时，结构受到较大的倾覆弯矩，且过窄的踵板不利于双排桩的布置；当高宽比过小时，结构受到较大的竖向力，将极大增加挡土墙底板与桩基的受力，且过宽的踵板会导致挡土墙底板产生较大的挠曲变形，不满足挡土墙底板相对刚度的假定。
为分析结构合适的高宽，分别取墙高h为7，8，9，10，11，12和13 m，BL为4.5 m，BL′为3.5 m，计算高宽比为1.4，1.6，1.8，2.0，2.2，2.4和2.6时的结构受力变形，结果如图4所示。
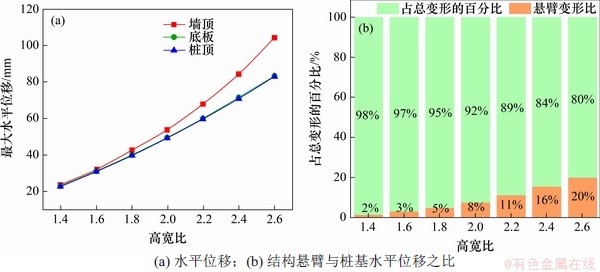
图4 不同高宽比组合结构变形特征
Fig. 4 Deformation characteristics of combined structure with different height to width ratios
分析结构水平位移可知：结构水平位移随高宽比的增长呈放大趋势，桩顶与底板水平位移呈线性增加，由于悬臂段的挠曲变形，墙顶位水平位移呈抛物线型增长，因此结构水平位移主要由桩基水平变形与悬臂段水平变形为主。当高宽比小于1.6时，桩基水平变形量占总变形量的95%以上，结构悬臂段未发挥作用。因此，在设计时高宽比取值不宜过小，否则该结构上部悬臂式挡土墙的设计将失去意义。综上所述，综合考虑结构内力与变形受高宽比的影响，建议双排桩基悬臂式挡土墙结构设计高宽比为1.6~2.0。
2.1.2 横向桩间距
双排桩基悬臂式挡土墙结构横向桩间距为内外排桩的中心距，在挡土墙结构尺寸不变的前提下，以底板中轴线对称移动内外排桩的位置，分别取横向桩间距BL为3.0，4.5，6.0和7.5 m(即2倍、3倍、4倍和5倍桩径)，墙高h为11 m，BL′为3.5 m时，分析横向桩间距对结构受力与变形的影响，计算结果如图5所示。
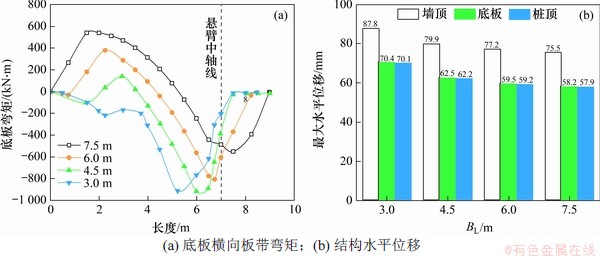
图5 不同横向桩间距组合结构变形特征
Fig. 5 Deformation characteristics of combined structure at different transverse pile spacings
底板弯矩随着桩间距的增大，由负弯矩为主向正弯矩为主转变。在底板长度不变的前提下，当桩间距过小时，底板存在较长悬臂段，当桩间距过大时，底板存在较长跨中段，底板受力均不合理。因此综合考虑弯矩变化趋势，建议横向桩间距取值为3~4倍的桩径。由结构水平位移变化趋势可知，结构最大水平变形位于墙顶位置，其值随横向桩间距的增大而减小，此时挡墙高度固定，悬臂段水平位移随着横向桩间距增加而减小，说明横向桩间距越小，底板的旋转变形量越大，为保证结构稳定性建议桩间距不应过小。综上所述，结合横向桩间距对结构内力与变形的影响，建议值内外排桩横向桩间距取值为3~4倍桩径。
2.1.3 纵向桩间距
双排桩基悬臂式挡土墙结构纵向桩间距为结构沿线路方向各排桩的中心距，结构桩基沿纵向多排等距布置，在挡土墙结构尺寸不变的前提下，分别取纵向桩间距BL′为3.0，4.5，6.0和7.5 m(即2倍、3倍、4倍和5倍桩径)，墙高h为11 m，BL为6 m时，分析纵向桩间距对结构受力与变形的影响，如图6所示。
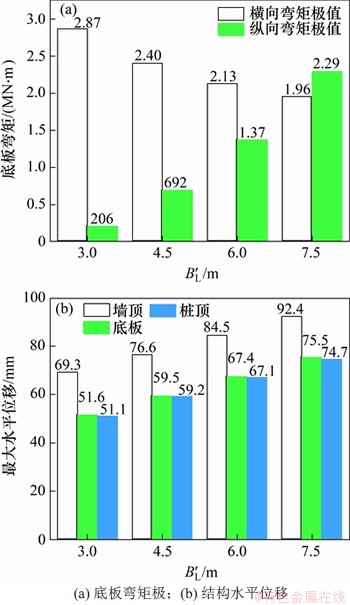
图6 不同纵向桩间距组合结构变形特征
Fig. 6 Deformation characteristics of combined structure at different longitudinal pile spacings
由于底板与桩基组成空间框架结构，底板沿纵向与横向均受弯矩作用，当纵向桩间距增大时，底板沿横向每延米范围内弯矩极值逐渐减小，沿纵向每延米范围内弯矩极值逐渐增大，且纵向弯矩增长速率较大。当纵向桩间距为4~5倍桩径时，底板弯矩最小。分析结构水平位移可知：结构水平位移随纵向桩间距的增长呈线性增大，这是由于单幅结构上部荷载随纵向桩间距的增长等比例增大所致。综上所述，结合结构受力与经济性指标，建议纵向桩间距为3~5倍桩径，设计时应核算底板在沿线路纵向与横向2个方向的弯矩。
2.2 挡土墙悬臂段计算方法
初步拟定出试算的墙身截面尺寸，墙高是根据工程需要确定的，墙顶宽不小于30 cm。墙背与墙面取竖直面，因而定出挡土墙悬臂段的截面尺寸。
当墙后填土为砂性土(重度γs=20 kN·m3，内摩擦角φs=20°)和黏性土(γc=20 kN·m3，φc=20°，黏聚力cc=20 kPa)，采用库仑理论(综合内摩擦角法)和朗金理论，分别计算悬臂高度为6，9和12 m的悬臂式挡墙，考虑宽高比为0.3，0.4，0.5，0.6和0.7时，作用在挡墙悬臂段的水平土压力合力，结果如图7所示。
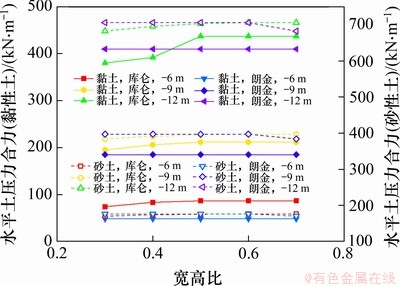
图7 悬臂式挡墙水平土压力
Fig. 7 Horizontal earth pressure of cantilever retaining wall
由图7可知：若墙后填土为黏性土，当踵板宽度较小时，朗金土压力略大于库仑土压力，当踵板宽度较大时，库仑理论考虑第二破裂面，库仑土压力与朗金土压力相等。从设计安全的角度出发，建议选用郎金土压力理论计算墙后土压力。
同样，若墙后填土为黏性土时，建议选用换算综合内摩擦角法的库仑土压力理论计算墙后土压力。计算时，以墙踵下边缘与悬臂上边缘连线的斜面作为假想墙背，当该连线的倾角大于临界角时，墙后填土中将出现第二破裂面，则应按第二破裂面理论计算土压力。
2.3 空间框架结构设计方法
首先根据挡土墙高度以及合适的高宽比(1.6~2.0)，初步拟定墙踵板宽度以及整个挡土墙底板宽度，接着根据地层地质情况拟定桩基布置形式以及受荷段长度与锚固段长度。
2.3.1 外荷载计算
将底板上部所有外荷载(包括挡土墙悬臂段传递的内力、结构自重以及土压力等)换算为作用在底板底面中心点的竖向合力N，水平合力H以及换算弯矩为M。
桩基悬臂段挡土墙结构设计理论定义桩基锚固段以上的部分为桩基受荷段，以土压力作为外力设计时，可简化为三角形或梯形分布。内排桩内侧土压力按主动土压力考虑，内外排桩间土压力按静止土压力考虑，外排桩外侧土压力取静止土压力计算；锚固段按文克尔弹性地基理论计算，计算时外荷载仅考虑由于锚固段顶端位移产生的桩侧土体横向抗力作用，地基反力系数为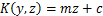
(其中，
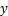为桩的水平位移；
为计算点深度；
为土的水平抗力系数；
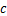为常数)。
2.3.2 空间框架结构内力计算
空间框架结构由挡土墙底板、桩基受荷段和桩基锚固段组成，受力与变形情况复杂，结构内力计算需结合边界条件与协调变形条件，从整体到局部再到整体反复计算，计算流程如下：
1) 考虑空间框架整体结构，计算上部荷载在挡土墙底板中心的竖向合力N、水平合力H、换算弯矩为M以及内外排桩基受荷段的土压力强度q1内，q2内，q1外和q2外，如图8所示。其中，h内和h外分别为内外桩锚固段长度；l0内和l0外分别为内外桩自由段长度。
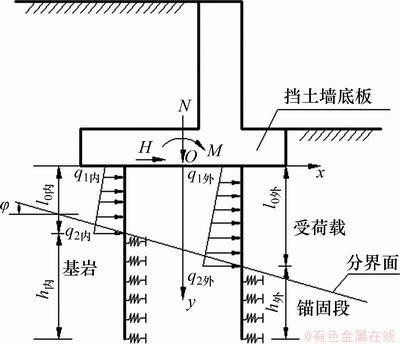
图8 桩基受荷段计算模型图
Fig. 8 Calculation model diagram of loaded section of pile foundation
2) 分别考虑各排桩受荷段，计算由桩周外荷载引起的受荷段顶部剪力Qq、弯矩Mq与受荷段底部的剪力Ql0、弯矩Ml0。
3) 考虑空间框架整体结构，根据结构尺寸与地基土层情况推到桩顶刚度系数ρ1，ρ2，ρ3和ρ4；其值可参照“桥涵设计规范”桩基础进行计算。
4) 考虑空间框架整体结构，求解挡土墙底板的水平位移a、竖向位移b、底板绕坐标原点O的转角β。
5) 分别考虑单桩结构，计算各桩顶(与底板连接处)的轴向力Ni、横向力Qi和弯矩Mi，再将Qi和Mi与Qq和Mq相加起来，得到各桩顶的剪力Q和弯矩M，以及桩基锚固段顶部的剪力Q0和弯矩M0。
6) 分别考虑各桩锚固段，按锚固段计算方法求出任一深度处的桩基截面中的剪力、弯矩和构件侧面岩土体的横向压应力。
7) 根据底板上部外荷载与各桩桩顶处轴力与弯矩计算底板内力。
2.4 软弱土地基工况稳定性检算
以桩基托梁式挡土墙为代表的桩承式支挡结构往往不需要进行抗滑移稳定性检算与抗倾覆稳定性检算与地基承载力检算。但当支挡结构在软弱土地区应用时，仍发生滑移以及倾覆破坏的可能性。因此从桩基悬臂式挡土墙结构受力与变形的角度出发，提出桩基悬臂式挡土墙结构的稳定性检算方法。
2.4.1 抗剪切检算
由桩基悬臂式挡土墙受力特点可知，悬臂式挡墙与桩基形成稳定刚架结构抵抗上部荷载与变形。当挡墙发生水平滑移破坏时，桩基势必在桩顶位置发生水平剪切破坏，因此，桩基悬臂式挡土墙结构抗滑移稳定性检算的实质为桩基桩顶水平抗剪强度检算，如图9所示。
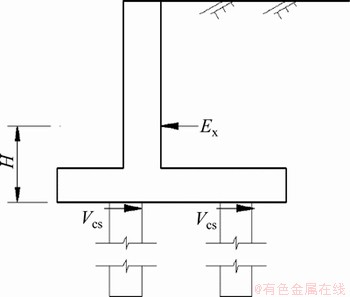
图9 桩基悬臂式挡土墙抗剪切检算图
Fig. 9 Shear resistance check chart of pile foundation cantilever retaining wall
桩基悬臂式挡土墙滑动稳定系数Kc为
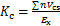(1)
式中：Vcs为桩基础斜截面受剪承载力；n为单幅挡土墙桩基数量；Ex为单幅挡土墙水平土压力和。
2.4.2 抗倾覆稳定性检算
当桩基悬臂式挡土墙有倾覆的可能性时，假定该结构绕外桩桩顶转动，此时内桩由受压状态向受拉状态转换，由结构上部挡土墙自重、土体自重与内桩抗拔力提供抗倾覆力矩，由挡土墙水平土压力提供倾覆力矩，如图10所示。
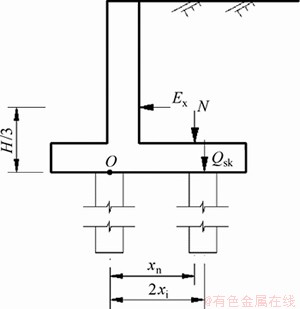
图10 桩基悬臂式挡土墙抗倾覆稳定性检算图
Fig. 10 Overturning stability check chart of pile foundation cantilever retaining wall
桩基悬臂式挡土墙滑动稳定系数K0为：
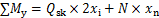(2)
(3)
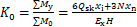(4)
式中：My为抗倾覆力矩；M0为倾覆力矩；N为挡墙自重与底板上部土体自重竖向合力；xn为合力N距外桩桩顶水平距离；Ex为挡墙悬臂段水平土压力合理；Qsk为单桩总极限侧摩阻力；2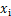
为Qsk距外桩桩顶水平距离。
根据“建筑桩基技术规范”中相关规定：
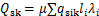(5)
式中：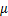
为桩周长；qsik为桩周第i层土的极限侧阻力；li为桩周第i层土的厚度；λi为桩周第i层土的抗拔折减系数。
2.5 结构承载力设计
2.5.1 正截面设计
桩基悬臂式挡土墙结构桩基主要承受结构传递的竖向荷载与弯矩。一般情况下，桩基按受弯构件设计，根据GB 50010—2010“混凝土结构设计规范”中相关规定，对于矩形截面构件，其正截面受弯承载力的计算公式如下：
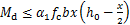(6)
式中：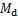
为弯矩设计值；α1为系数；fc为混凝土轴心抗压强度设计值，按GB 50010—2010“混凝土结构设计规范”中4.1.4取值；b为矩形截面的宽度；x为混凝土受压区高度；h0为截面有效高度。
2.5.2 斜截面设计
桩基悬臂式挡土墙结构底板与悬臂连接处、底板与桩基连接处等位置属于结构薄弱环节，在结构承载力设计时还需对这些位置进行斜截面设计。根据GB 50010—2010“混凝土结构设计规范”中相关规定，对于普通混凝土矩形截面，当仅配置箍筋时，其斜截面的受剪承载力应符合以下规定：
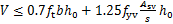(7)
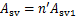(8)
式中：V为构件斜截面上的最大剪力设计值；Asv为配置在同一截面内箍筋各肢的全部截面面积；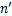
为在同一截面内箍筋的肢数；Asv1为单肢箍筋的截面面积；s为沿构件长度方向的箍筋间距；fyv为箍筋抗拉强度设计值，按GB 50010—2010“混凝土结构设计规范”表4.2.3-1中的fy取值。
3 案例分析
为了验证设计理论的合理性，通过在典型断面埋设元器件，来测试桩基悬臂式挡墙结构随施工进程产生的内力变化及变形情况。
3.1 工程概况
试验测试试验断面，该测试断面均为桩基所在断面。通过埋设相关测试元器件，测试外桩、内桩、悬臂和底板的土压力分布与应力规律。
该地区是丘陵地形、沟壑丘陵地形、起伏地形，地面高程320~395 m，相对高度差约75 m，自然横坡通常为16°~40°，局部最大70°。丘陵上方的土壤层很薄，基岩部分暴露，并且表面大部分为干旱土地。
悬臂挡土墙最大墙高为9.5 m，钻孔灌注桩的参数如下：桩径为1.5 m，桩长约为20 m，桩横向间距为4.8 m，纵向间距为3.5 m，挡土墙踵板宽度为4.4 m，趾板宽为2.0 m，代表性横断面如图11所示。
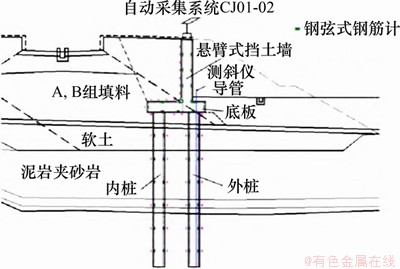
图11 代表性横断面
Fig. 11 Representative cross-sections
3.2 结构内力测试结果分析
3.2.1 悬臂内力测试结果分析
对3个时间点的悬臂弯矩分布情况进行分析。将该断面悬臂段钢筋计所测钢筋应变进行换算，得到悬臂段由浇筑完成后填土过程中弯矩分布，同时对填土厚度8 m的工况进行理论计算，并将两者结果进行对比如图12所示。
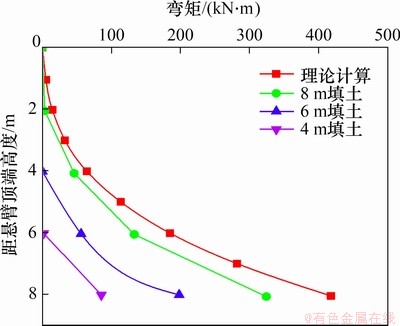
图12 悬臂段弯矩
Fig. 12 Cantilever section bending moment
由图12可知：挡墙悬臂段弯矩自上而下基本呈抛物线形分布，测量值近似于理论计算值，可以表明理论计算的准确性。
3.2.2 底板内力测试结果分析
对3个时间点的挡墙底板弯矩分布情况进行分析。将该断面挡墙底板钢筋计所测钢筋应变进行换算，得到底板由浇筑完成后填土过程中弯矩分布，如图13所示。
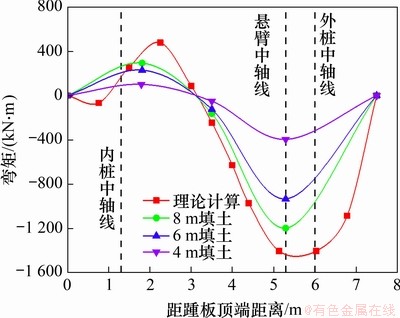
图13 底板弯矩
Fig. 13 Base plate bending moment
由图13可知：挡墙浇筑完成后进行填土过程中，底板弯矩随填土高度的增加而增加，这是由于挡墙悬臂段承受的土压力显著增长导致弯矩传递给底板所致。
3.2.3 外桩内力测试结果分析
由于该工地地层分布较为平缓，桩基弯矩主要由上部挡墙传递荷载导致。本节分别对挡墙修筑完成后填土为4，6和8 m时的外桩弯矩分布进行分析，如图14所示。
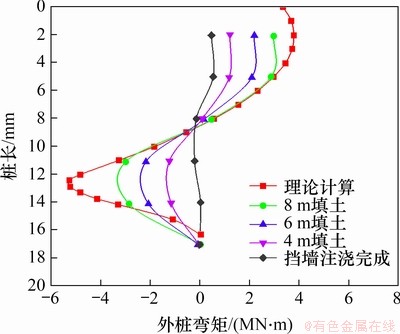
图14 外桩弯矩
Fig. 14 External pile bending moment
由图14可知：相比刚浇筑完成的情况，进行填土后外桩上正负弯矩绝对值均有所增大，且随着填土厚度的增大外桩弯矩也随之增大。正弯矩较大的原因是上部挡墙传递弯矩导致的应力集中。
3.2.4 内桩内力测试结果分析
由于该工地地层分布较为平缓，桩基弯矩主要由上部挡墙传递荷载导致。分别对挡墙修筑完成后填土为4，6和8 m时内桩弯矩分布进行分析，如图15所示。
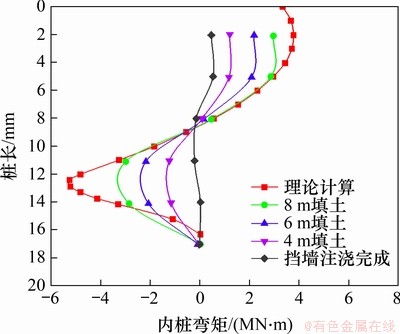
图15 内桩弯矩
Fig. 15 Internal pile bending moment
由图15可知：同外桩弯矩的情况相似，相比刚浇筑完成的情况，进行填土后长桩上正负弯矩绝对值均有所增大，且随着填土厚度的增大，内桩弯矩也随着增大。
3.3 结构变形测试结果分析
试验重点测量结构挡墙悬臂段水平位移，通过全站仪对挡墙悬臂段自上而下的观测点进行连续观测。以挡墙浇筑完成后的测试值为零点，分析挡墙悬臂段水平位移随填土高度的变化情况，如图16所示。
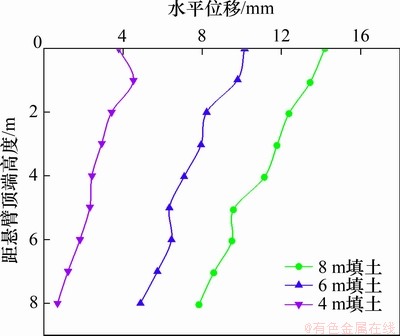
图16 挡墙悬臂段水平位移图
Fig. 16 Horizontal displacement diagram of cantilever section of retaining wall
由图16可知：随着路基填料的填筑，挡墙悬臂段水平位移呈稳定上升趋势，施工完毕后，最大水平位移发生在悬臂段顶端，约为14.2 mm，说明双排桩基悬臂式挡土墙能较好地控制路基水平变形。
3.4 稳定性检算
根据双排桩基悬臂式挡土墙结构计算理论，本小节选取试验段桩基悬臂式挡土墙结构及岩土体参数进行结构受力与变形试算。
1) 挡墙悬臂段受力。根据计算理论，假设挡墙后侧填料参数为容重γ=21 kN/m3，φ=25°，c=20 kPa，挡墙悬臂段土压力选用库仑土压力理论计算，取挡墙后侧填土表面均布荷载换算土柱高度h0=1 m，则沿线路方向单位长度范围内挡墙悬臂段土压力合力E为
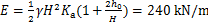(9)
2) 空间框架结构段受力。取双排桩基悬臂式挡土墙结构单跨范围内(沿线路方向长度L=10.08 m)的下部空间框架结构进行计算，换算上部荷载为：水平合力H=EL=2 422.81 kN、竖向合力N=14 122.03 kN、底板中心处弯矩M=-3 25.91 kN·m。力和位移计算方法如表1所示。
3) 稳定性检算。检算内容如表2所示。
表1 力和位移计算方法
Table1 Calculation method of internal force and displacement
表2 检算内容
Table 2 Content of audit
综上所示，该工点桩基悬臂式挡土墙结构满足稳定性检算。
4 结论
1) 通过结构受力和变形计算分析，提出了双排桩基悬臂式挡土墙结构设计的高宽比建议值为1.6~2.0，结构横向桩间距建议值为3~4倍桩径，纵向桩间距建议值为3~5倍桩径。
2) 提出了适用于双排桩基悬臂式挡土墙土压力计算方法建议：黏性土填料采用库仑理论，砂性土填料采用郎金理论计算土压力。
3) 提出双排桩基悬臂式挡土墙设计分为结构截面尺寸拟定及钢筋混凝土结构设计2部分。确定结构各部件的断面尺寸是通过试算法进行的，其做法是先拟定挡土墙部分截面的试算尺寸，计算作用其上的土压力，通过全部稳定性验算来，最终确定踵板的宽度以及桩基的尺寸。
4) 桩基悬臂式挡墙的悬臂段内力、底板内力以及桩基内力均随着路基填筑高度的增加而增大，并与理论计算结果类似，试验段桩顶最终沉降约为14.2 mm，说明双排桩基悬臂式挡土墙能较好地控制路基水平变形。
参考文献：
[1] 李海光. 新型支挡结构设计与工程实例[M]. 北京: 人民交通出版社, 2011: 36-37.
LI Haiguang. Design and engineering example of new retaining structure[M]. Beijing: People's Communications Press, 2011: 36-37.
[2] 周珩. 桩基悬臂式新型支挡结构受力机理与设计计算[D]. 成都: 西南交通大学, 2013: 50-52.
ZHOU Heng. Study on mechanical behavior and design optimization of new piles foundation cantilever retaining structure on the slope[D]. Chengdu: Southwest Jiaotong University, 2013: 50-52.
[3] 姚裕春, 李安洪, 苏谦. 陡坡椅式桩板结构受力模式及计算方法分析[J]. 铁道工程学报, 2016, 33(8): 71-76.
YAO Yuchun, LI Anhong, SU qian. Analysis of force model and calculation method of chair-shaped sheet-pile structure constructed on steep slop[J]. Journal of Railway Engineering Society, 2016, 33(8): 71-76.
[4] 刘国楠, 胡荣华, 潘效鸿, 等. 衡重式桩板挡墙受力特性模型试验研究[J]. 岩土工程学报, 2013, 35(1): 103-110.
LIU Guonan, HU Ronghua, PAN Xiaohong, et al. Model tests on mechanical behaviors of sheet pile wall with relieving platform[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(1): 103-110.
[5] 雷正敏. 高烈度地区双排桩基托梁浸水挡土墙的应用研究[J]. 铁道建筑, 2020, 60(11): 84-87.
LEI Zhengmin. Application study of double-row pile foundation joist water-immersed retaining wall in high-intensity areas[J]. Railway Construction, 2020, 60(11): 84-87.
[6] 芮瑞, 翟玉新, 王磊, 等. 桩承式挡墙路堤三维土压力分布与变形特性试验[J]. 岩石力学与工程学报, 2021, 40(3): 590-606.
RUI Rui, ZHAI Yuxin, WANG Lei, et al. Xu Yangqing. Three-dimensional soil pressure distribution and deformation characteristics of pile-supported retaining wall embankment[J]. Chinese Journal of Rock Mechanics and Engineering, 2021, 40(3): 590-606.
[7] 谢明星, 郑俊杰, 曹文昭, 等. 联合支挡结构中抗滑桩设计参数分析与优化[J]. 华中科技大学学报(自然科学版), 2019, 47(7): 1-7.
XIE Mingxing, ZHENG Junjie, CAO Wenzhao, et al. Analysis and optimization of design parameters of anti-slide piles in joint supporting structure[J]. Journal of Huazhong University of Science and Technology(Natural Science Edition), 2019, 47(7): 1-7.
[8] REESE L C. Analysis of laterally loaded piles in weak rock[J]. Journal of Geotechniacl and Geonvironmental Engineering, 1997, 123(11): 2-3.
[9] 焦峰. 扶壁式挡土墙结构的最优设计[D]. 兰州: 兰州理工大学, 2004: 66-68.
JIAO Feng. Optimal design of buttressed retaining wall structure[D]. Lanzhou: Lanzhou University of Technology, 2004: 66-68.
[10] 姚裕春, 袁碧玉. 铁路高填方下沉式站房收坡结构选择创新方法分析[J]. 高速铁路技术, 2018(1): 16-20.
YAO Yuchun, YUAN Biyu. Selection of innovative methods for reinforcing structure for high fill sunken railway station [J]. High Speed Railway Technology, 2018(1): 16-20.
[11] 姚裕春, 李安洪, 袁碧玉, 等. 桩基悬臂式、扶臂式挡土墙: 中国, 201220442371. 1[P]. 2013-04-10.
YAO Yuchun, LI Anhong, YUAN Biyu, et al. Pile foundation cantilever retaining wall and counterfort retaining wall: China, 201220442371. 1[P]. 2013-04-10.
[12] 姚裕春, 袁碧玉. 无砟轨道铁路陡坡路基加固结构创新方法分析[J]. 高速铁路技术, 2015, 6(4): 31-35.
YAO Yuchun, YUAN Biyu. Analysis on innovative methods for reinforcing structure of steep slope subgrade of ballastless track railway[J]. High Speed Railway Technology, 2015, 6(4): 31-35.
[13] 姚裕春, 苏谦, 周珩, 等. 双排桩基悬臂式挡墙受力及变形特征研究分析[J]. 铁道工程学报, 2018, 35(6):11-15.
YAO Yuchun, SU Qian, ZHOU Heng, et al. Research and analysis on stress and deformation characteristics of cantilever retaining wall with double row pile foundation [J]. Journal of Railway Engineering, 2018, 35(6): 11-15.
[14] 任庆昌. 桩基悬臂式挡墙在路基帮宽工程中的应用[J]. 铁道工程学报, 2015, 32(2): 43-47, 63.
REN Qingchang. Application of cantilever retaining wall of pile foundation in subgrade width engineering[J]. Journal of Railway Engineering, 2015, 32(2): 43-47, 63.
[15] 周珩, 苏谦, 杨智翔, 等. 软土地基双排桩基础悬臂式挡土墙受力变形的现场测试及数值模拟分析[J]. 铁道建筑, 2019, 59(3): 88-91.
ZHOU Heng, SU Qian, YANG Zhixiang, et al. Field test and numerical simulation analysis of cantilever retaining wall with double row pile foundation on soft soil foundation [J]. Railway Architecture, 2019, 59 (3): 88-91.
[16] 周珩, 苏谦, 姚裕春, 等. 双排桩基悬臂式挡土墙结构计算方法研究[J]. 铁道科学与工程学报, 2019, 16(3): 654-663.
ZHOU Heng, SU Qian, YAO Yuchun, et al. Study on calculation method of cantilever retaining wall with double row pile foundation[J]. Journal of Railway Science and Engineering, 2019, 16 (3): 654-663.
[17] 刘杰. 高边坡双排桩与悬臂式挡墙组合结构受力特性研究[D]. 衡阳: 南华大学, 2018: 17-19.
LIU Jie. Study on mechanical characteristics of composite structure of double row piles and cantilever retaining wall on high slope[D]. Hengyang: Nanhua University, 2018: 17-19.
[18] 姚裕春, 李安洪, 李井元, 等. 双排桩基悬臂式挡土墙参数影响研究分析[J]. 高速铁路技术, 2018, 9(5): 11-16, 37.
YAO Yuchun, LI Anhong, LI Jingyuan, et al. Research and analysis on the influence of parameters of cantilever retaining wall with double-row pile foundation[J]. High-speed Railway Technology, 2018, 9(5): 11-16, 37.
(编辑 杨幼平)
收稿日期： 2021 -03 -10； 修回日期： 2021 -04 -28
基金项目(Foundation item)：国家自然科学基金资助项目(51978674) (Project(51978674) supported by the National Natural Science Foundation of China)
通信作者：陈晓斌，博士，教授，从事路基动力学研究；E-mail: chen_xiaobin@csu.edu.cn
DOI: 10.11817/j.issn.1672-7207.2021.07.021
引用格式： 谢康, 周珩, 张乐, 等. 桩基悬臂式挡墙组合结构设计理论研究[J]. 中南大学学报(自然科学版), 2021, 52(7): 2349-2359.
Citation: XIE Kang, ZHOU Heng, ZHANG Le, et al. Theoretical research on design of combined structure of cantilever retaining wall of pile foundation[J]. Journal of Central South University(Science and Technology), 2021, 52(7): 2349-2359.
