Explicit incremental-update algorithm for modeling crystal elasto-viscoplastic response in finite element simulation

   LI Hong-wei(李宏伟), YANG He(杨  合), SUN Zhi-chao(孙志超)  

College of Materials Science and Engineering, Northwestern Polytechnical University, Xi’an 710072, China

Received 10 April 2006; accepted 25 April 2006

Abstract: Computational stability and efficiency are the key problems for numerical modeling of crystal plasticity, which will limit its development and application in finite element (FE) simulation evidently. Since implicit iterative algorithms are inefficient and have difficulty to determine initial values, an explicit incremental-update algorithm for the elasto-viscoplastic constitutive relation was developed in the intermediate frame by using the second Piola-Kirchoff (P-K) stress and Green stain. The increment of stress and slip resistance were solved by a calculation loop of linear equations sets. The reorientation of the crystal as well as the elastic strain can be obtained from a polar decomposition of the elastic deformation gradient. User material subroutine VUMAT was developed to combine crystal elasto-viscoplastic constitutive model with ABAQUS/Explicit. Numerical studies were performed on a cubic upset model with OFHC material (FCC crystal). The comparison of the numerical results with those obtained by implicit iterative algorithm and those from experiments demonstrates that the explicit algorithm is reliable. Furthermore, the effect rules of material anisotropy, rate sensitivity coefficient (RSC) and loading speeds on the deformation were studied. The numerical studies indicate that the explicit algorithm is suitable and efficient for large deformation analyses where anisotropy due to texture is important.

Key words: crystal plasticity; explicit algorithm; constitutive relation; FE simulation; ABAQUS/Explicit

1 Introduction

The microscopic constitutive relation (MCR) of crystal material is established on the base of crystal plasticity theory. It describes the mechanism of crystalline dislocation slip in plastic deformation of crystal. The combination of MCR with FEM, namely, crystal plastic finite element method (CPFEM), is an effective way to simulate and analyze crystal deformation in microscopic scales. CPFEM was proposed first by HILL and RICE[1], and the numerical method was established by PIERCE et al[2]. Herefrom, a wide use of CPFEM has been achieved in the fields of material and mechanics.

Since most materials are rate dependent, rate- dependent crystal plasticity is widely used. Whereas, it is difficult to achieve the numerical application of rate-dependent crystal plasticity in FEM due to the high-order exponent hardening equations, which results in the computational instability. To ensure a stable calculation, robust implicit iterative algorithms were introduced. KALIDINDI et al[3] deduced a time- incremental crystal plasticity model and adopted Newton iteration method for the solution of the constitutive equations. To ensure computational convergence, additional limits were imposed on the stress increment. SARMA and ZACHARIA[4] provided an integration algorithm based on a time-incremental formula of the elastic deformation gradient. In the same way, the change of the elastic deformation gradient was limited to aid convergence. Three ordinary differential equations of the crystal plastic constitutive relation were derived by RASHID and NEMAT-NASSER[5], and a weighted residual method was adopted for the approximate solutions of these equations. RAPHANEL et al[6] proposed an equilibrium search method based on the second-order RUNGE-KUTTA integration scheme, which achieved higher precision and a quadratic rate of convergence. However, it is still complicated. So, it can be concluded that plenty of iterations and the difficulty to determine initial iterative values make implicit algorithms inefficient and incompetent for simulations of large structure complex deformation process. Therefore, explicit algorithms are deduced to overcome these disadvantages. The algorithms are based on the linearization of the nonlinear constitutive relations. PIERCE et al[7] proposed a forward-gradient method (i.e. tangent-modulus method), which is widely used in the subsequent numerical study of crystal plasticity. Whereas, it leads to a stiff system in calculation, which requires very small time increment in order to obtain the desired accuracy and stability. So, a plastic-predictor elastic- corrector method was proposed by NEMAT-NASSER et al[8, 9], which solved the slip system shearing rates by the linearization of the deformation rate equation, instead of rate-dependent hardening equation. So, the approach keeps the high-order exponent hardening equation from calculations. Nevertheless, it is necessary to determine whether the slip systems are active, and to distinguish three different regimes based on the number of the active slip systems for the solution of the slip system shearing rates, which makes the approach complicated and inefficient. MCGINTY and MCDOWELL[10] proposed a new approach to identify active slip systems prior to determining their shearing rate, based on which a semi-implicit integration scheme was proposed.

It can be found that stability and efficiency of computation are the key problems for the numerical application of crystal plasticity in FEM. Except for algorithms, the frame in which the constitutive model is established does effects on computational efficiency as well. Most works are performed in current frame based on the constitutive relations in the form of objective stress rate. However, the vectors of slip systems in current frame are time-dependent, while, they are time- independent in reference and intermediate frames. So, DELANNAY et al[11] established a model of MCR in reference frame, which made it convenient to realize numerical application of crystal plasticity.

Herein, an explicit incremental-update model was proposed in the intermediate frame for modeling the elasto-viscoplastic constitutive response by using the second P-K stress and Green stain. Linear incremental equation of the stress increment was deduced by using Taylor series expansion of the rate-dependent hardening equation. The complete pivot Gaussian elimination method was adopted for the solution, which made the calculation simple and stable.

The following conventions will be used in the paper. The fourth-order elastic tensor and the second-order identity tensor were represented by C and 1 respectively. Tensors or vectors will be denoted by boldfaced italic. The product and inner product of two tensors A and B will be denoted by AB and A·B, respectively. The vector product of two vectors a and b will be denoted by a?b. The double dot metrix of the forth-order tensor C and second-order tensor A will be denoted by C:A. The product of tensor and vector v will be denoted by Av. Quantities of AB, Av, C:A, a?b and A·B have the following component representation: (AB)_ij = A_ikB_kj, (Av)_i = A_ikv_k, (C:A)_ij = C_ijklA_kl, (a?b)_ij = a_ib_j and  (A·B)_ij = A_ijB_ij.

2 Crystal kinematics and constitutive relations

2.1 Crystal kinematics

The general kinematics of the elastic-plastic deformation of crystal at finite strains was given by HILL and RICE [1], and developed by HILL and HAVNER[12]. HAVNER[13] provided a comprehensive account of the subject.

The total deformation gradient of finite strain from the reference frame to the current frame, F, was defined by

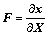                                   (1)

where  X and x denote the reference and current particle positions, respectively. The kinematics of crystal finite deformation is hinted in Fig.1.

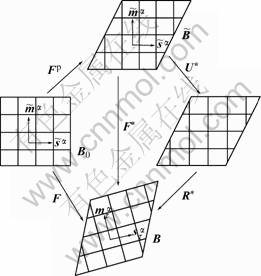
Fig. 1 Schematic diagram of single crystal kinematics

The hypothesis was adopted that material deformed plastically by crystalline slip, while the lattice underwent elastic deformation. So, the total deformation gradient has a multiplicative decomposition as

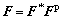                                 (2)

where 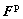  is the plastic deformation gradient due to shearing along crystallographic slip planes. The plastic deformation by slip was assumed to occur at constant volume with the orientation of the lattice remaining unchanged, so, det 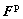=1 (plastic incompressibility). F^* is the elastic deformation gradient which includes any rigid rotation of the lattice, and can be obtained by

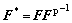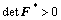,                       (3)

The velocity gradient in current frame is

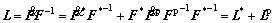  (4)

The plastic velocity gradient 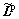 relative to the intermediate frame is expressed as a linear combination of the slip system shearing rates, 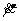, as follows:

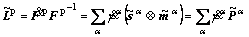      (5)

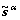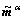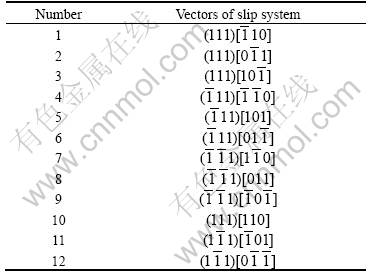
The dyadic product of the unit vector in the slip direction, , with the unit normal vector of the slip plane, , gives the Schmid orientation tensor, 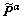, in the intermediate frame. Details of vectors of slip systems for FCC crystal with 12 {111}<110> type slip systems are presented in Table 1.

Table 1 Details of slip systems for FCC crystal

2.2 Constitutive relations

The elastic constitutive relations of crystalline material are presented in the intermediate frame:

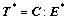                                 (6)

The strain measure is given by the Green strain tensor, E^*, defined in terms of the elastic deformation gradient, F^*, and the second-order identity tensor, 1, as

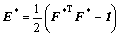                         (7)

The corresponding stress measure is the second P-K stress, T^*, which is the elastic work conjugate to the Green strain, given in terms of the Cauchy stress T by

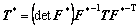                      (8)

The quantity,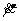, in Eqn.(5) is the plastic shearing rates on the slip system α due to crystalline slip, and is given in terms of resolved shear stress τ^α and a slip resistance s^α. Here, a rate-dependent slip model with the power law is employed.

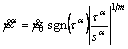                        (9)

where  m is RSC, 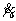 is the reference rate of shearing. The resolved shear stress is the component of the traction along the direction of slip, and is related to the second P-K stress and the Schmid tensor in the intermediate frame as

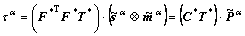     (10)

For metallic materials, the elastic stretch is usually infinitesimal. For this situation, the resolved shear stress 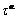 may, with impunity, be approximated by

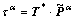                               (11)

The slip resistance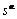 is taken to evolve as

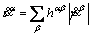                            (12)

where 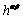  is the rate of strain hardening on slip system α due to a shearing on the slip system β, and is related to a single slip hardening rate, h^α, and the hardening matrix,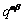, as

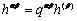 ( no sum on β )                 (13)

The hardening matrix,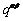, describes the latent hardening behavior of a crystallite, which is complicated as described in literature [14]. For the 12 {111}<110> slip systems of FCC crystals,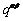is given by

                   (14)

where  q is the ratio of the latent hardening rate to the self-hardening rate given by ZHOU et al[15], and A is a 3×3 matrix fully populated by ones.

The model for the single slip hardening rate in Eqn.(13) proposed by KALIDINDI[3] is adopted.

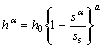                           (15)

where  h₀, a and s_s are the slip system hardening parameters.

3 Incremental-update algorithm

Assumption is adopted that t denotes the time at the start of the step, and τ = t +?t denotes the time at the end of the step. An evolution equation for 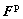 is presented as

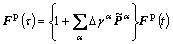                (16)

where the increment of shearing strain on a slip system is given by

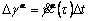                             (17)

Taylor series expansion of Eqn.(9), neglecting the high-order terms, is expressed as

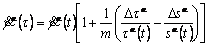           (18)

According to Eqn.(11), we obtained

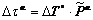                            (19)

Substitute Eqns.(3) and (7) into Eqn.(6),

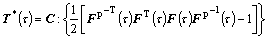  (20)

Let

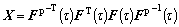               (21)

Then, substituting Eqn.(16) into Eqn.(21), we obtained

      (22)

Neglecting the 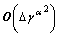 terms, Eqn.(22) may be rewritten as

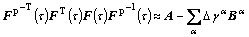     (23)

where

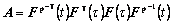                (24)

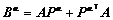                         (25)

Finally, substituting Eqn.(23) into Eqn.(20), we obtained

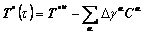                    (26)

where

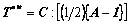                       (27)

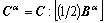                           (28)

Then, substituting Eqns.(17) and (18) into Eqn.(26), we obtained

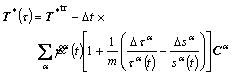       (29)

Rewriting Eqn.(29) in incremental form as

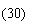
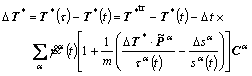
According to Eqn.(12), the incremental evolution of the slip system resistance is presented as

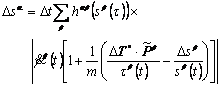         (31)

Eqn.(30) is solved for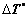, keeping  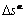fixed at its best available estimate. Since all values at the time t are known, Eqn.(30) is a linear equation set in terms of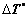. So, the complete pivot Gaussian elimination method is adopted for the solution. Then, a new  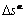is obtained based on  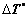and the old  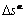through Eqn.(31). Then the recalculation of  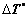is performed on the base of the new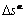. The loop is continued until both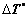and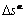satisfy the criterions as follows:

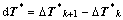, and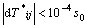

            (k=0,1,…)                     (32)

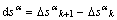, and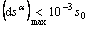

            (k=0,1,…; and α =1,2,…,12)      (33)

where  s₀ is the initial value of the slip resistance.

In the procedures, the time-independent slip systems (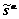,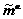), as well as the deformation gradient, the plastic deformation gradient, the second P-K stress and the slip resistance at the start of the step,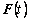,,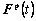 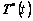and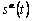, are known at first. We took all the initial values ofequal to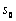, and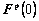equal to the second-order identity tensor. Additionally, an estimate of the deformation gradient at time τ,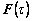, is given.

The procedures are as follows:

1) Compute A,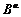,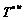and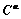using Eqns.(24), (25), (27) and (28), respectively;

2) Solve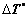and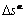through the loop of calculation by using Eqns.(30) and (31), and update 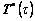and ;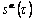

3) Update the plastic deformation gradient at the end of the step,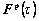, by using Eqn.(16). However, this does not ensure that 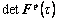is equal to unity. So, it is necessary to normalize 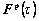by

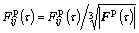                     (34)

4) Compute the elastic deformation gradient at the end of the increment according to Eqn.(2),

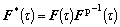                        (35)

5) Compute the Cauchy stress in current frame by

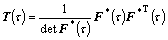                 (36)

6) The polar decomposition of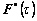 was used to compute the rotation,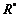, of the crystal lattice during the deformation,

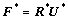                                (37)

Compute the reorientation of crystal lattice from

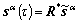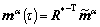 and            (38)

where 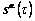, 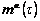represent α slip system in the current frame at time τ.

It is convenient to implement the algorithm in FE simulation by developing user subroutine VUMAT[16] on the platform of ABAQUS/Explicit.

5 Numerical results and analysis

To ensure the subroutine is reliable prior to its wide use, the simulation of compression model with single element is adopted, as shown in Fig.2, with the material of the annealed oxygen free high conductivity (OFHC) copper, whose parameters are shown in Table 2.

In the model of Fig.2, the length of side is 1 mm. The model is depressed with a speed of 20 mm?s^-1, and the total step time is 0.01 s. In addition, it is assumed that there is no friction on the faces.

The responses of the axial stress and logarithmic axial strain obtained in the simulations are compared with those obtained by using the implicit iterative algorithm and those from experiment in the literature [3], as shown in Fig.3. The agreement is satisfying, which demonstrates the subroutine is reliable.

Based on the above work, a cubic upset model with the side length of 10mm, meshed into 125 elements, was adopted for the simulations to do some research on the

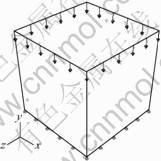
Fig. 2 Constraints situation in simple compression model

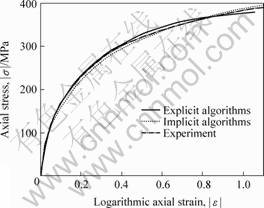
Fig. 3 Comparison of axial stress—strain responses in simple compression process

effects of material anisotropy done on the deformation process. Nephograms of the distribution of stress in 3D view, as well as nephograms of the distribution of strain in y-z view at the different stages of the deformation process are presented in Fig.4.

The non-uniform distribution of the stress and strain, as well as the obvious drum shapes shown in Fig. 4 indicate that material anisotropy do much effect on the deformation, even though the load is uniaxial.

In order to do some research on the effect rules of which loading speeds do on materials with different RSCs, the stress-strain responses of the material with the value 0.03 of RSC (m=0.03) under different loading speeds, and the stress-strain responses of materials with different RSCs under loading speed of 20 mm?s^-1 (v=20 mm?s^-1) were investigated. The curves are shown in Fig.5 and Fig.6, respectively.

In Fig.5, the loading speeds of 10, 50 and 100 m?ms^-1 are applied. It can be concluded that the axial stress increases with the increment of loading speed. Fig.6 shows that materials with RSCs of 0.02, 0.025 and

Table 2 Parameters of annealed OFHC copper

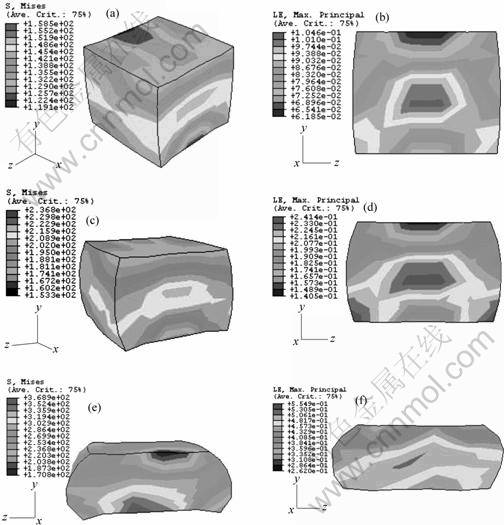
Fig. 4 Distribution of stress and strain with different deformation ratios δ: (a) Stress distribution, δ=10%; (b) Strain distribution, δ=10%; (c) Stress distribution, δ=20%; (d) Strain distribution, δ=20%; (e) Stress distribution, δ=40%; (f) Strain distribution, δ=40%

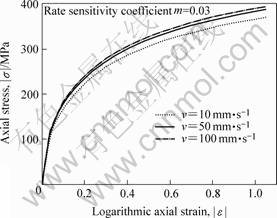
Fig. 5 Stress—strain responses of material with m=0.03 under different loading speeds

0.03 undergo the deformation, and the axial stress increases with the increment of RSC. This rules agree well with the nature.

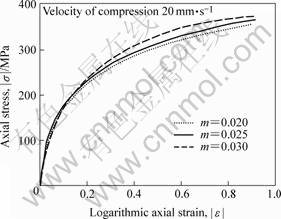
Fig. 6 Stress—strain responses of material with different rate sensitivity coefficients under loading speed of 20 mm?s^-1

The simulations on the cubic upset model above were performed on the personal computer with the configuretion of Pentium 4, 2.60 GHz CPU and 2.59 GHz, 2.00 GB memory. Computational efficiency was compared with the simulations by using the implicit algorithm in literature [17], which is shown in Table 3.

Table 3 Comparison of computational efficiency between explicit and implicit algorithm

From Table 3, it can be seen that the explicit algorithm proposed is greatly efficient.

6 Conclusions

The explicit incremental-update algorithm of crystal elasto-viscoplastic constitutive relation was presented by using the second P-K stress and Green stain in the intermediate frame. The increments of stress and the slip resistance are solved by a loop calculation of linear equations set, which is simplified on the base of the linearization of the nonlinear equations. User material subroutine VUMAT is developed in the light of the algorithm to implement crystal elasto-viscoplastic constitutive model in FE simulation. The comparison of the numerical results with those obtained by using implicit iterative algorithm and those from experiment demonstrates the explicit algorithm in the paper is reliable. Further studies show that material anisotropy, RSC and loading speed do effects on the deformation, the axial stress increases with the increment of loading speed and RSC. The studies indicate that the explicit algorithm is reliable and efficient.

[1] Hill R, Rice J R. Constitutive analysis of elastic-plastic crystals at arbitrary strain [J]. J Mech Phys Solids, 1972, 20(6): 401-413.

[2] Pierce D, Asaro R J, Needleeman A. Material rate dependence and localized deformation in crystalline solids [J]. Acta Metall, 1983, 31(12): 1951-1976.

[3] Kalidindi S R, Bronkhorst C A, Anand L. Crystallographic texture evolution in bulk deformation process of fcc metals [J]. J Mech Phys Solids, 1992, 40(3): 537-569.

[4] SARMA G, ZACHARIA T. Integration algorithm for modeling the elasto-viscoplastic response of polycrystalline materials [J]. J Mech Phys Solids, 1999, 47(6): 1219-1238.

[5] RASHID M M, NEMAT-NASSER S. A constitutive algorithm for rate- dependent crystal plasticity [J]. Computer Methods in Applied Mechanics and Engineering, 1992, 94(2): 201- 228.

[6] Raphanel J L, Ravichandran G, Leroy Y M. Three- dimensional rate-dependent crystal plasticity based on Runge-Kutta algorithms for update and consistent linearization [J]. International Journal of Solids and Structures, 2004, 41(22-23): 5995-6021.

[7] PEIRCE D, SHIH C F, NEEDLEMAN A. A tangent modulus method for rate dependent solids [J]. Computers and Structures, 1984, 18(5): 875-887.

[8] NEMAT-NASSER S, OKINAKA T. A new computational approach to crystal plasticity: fcc single crystal [J]. Mechanics of Materials, 1996, 24(1): 43-57.

[9] NEMAT-NASSER S, NI L, OKINAKA T. A constitutive model for fcc crystals with application to polycrystalline OFHC copper [J]. Mechanics of Materials, 1998, 30: 325-341.

[10] MCGINTY R D, MCDOWELL D L. A semi-implicit integration for rate independent finite crystal plasticity [J]. Int J Plasticity, 2006, 22(6): 996-1025.

[11] Delannay L, Jacques P J, Kalidindi. S R. Finite element modeling of crystal plasticity with grains shaped as truncated octahedrons [J]. Int J Plasticity, 2006. (in press)

[12] HILL R, HAVNER KS. Perspectives in the mechanics of elastoplastic crystal [J]. J Mech Phys Solids, 1982, 30(1-2): 5-22.

[13] HAVNER K S. Finite plastic deformation of crystalline solids [M]. New York: Cambridge, 1992.

[14] KUMAR A V, YANG C. Study of work hardening models for single crystals using three dimensional finite element analysis [J]. Int J Plasticity, 1999, 15(7): 737-754.

[15] Zhou Y, Neale K W, Tóth L S. A modified model for simulating latent hardening during the plastic deformation of rate-dependent fcc polycrystals [J]. Int J Plasticity, 1993, 9(8): 961-978.

[16] ABAQUS User’s Manual, 2004. Version 6.5, ABAQUS, Inc.

[17] LI H W, YANG H, SUN Z C. Research on the implicit algorithm and numeralization of microscopic constitutive relation [J]. Mater Sci Technol, 2006. (Accepted)

(Edited by LI Xiang-qun)

Foundation item: Project(50335060) supported by the National Natural Science Foundation of China; Project (50225518) supported by the National Science Fund for Distinguished Young Scholars of China; Project supported by the Scientific and Technological Innovation Foundation for Youth NPU Teachers

Corresponding author: Yang He; Tel: +86-29-88495632; E-mail: yanghe@nwpu.edu.cn