INS/GPS组合导航中带有置信度的抗差Kalman滤波算法
潘倩兮,赵龙,张常云
(北京航空航天大学 控制一体化技术国家级重点实验室,北京,100191)
摘要:针对INS/GPS组合导航中GPS信号出现观测异常的情况,设计抗差Kalman滤波算法。该算法在建立可靠运动学模型的基础上,根据预测残差统计量来判断观测异常。在一定的置信度下,当检测到异常发生时,使相应的观测协方差阵膨胀,降低观测量的可信度,更多地利用动力学模型的信息,从而提高滤波精度。仿真实验证实了该算法的有效性和可靠性。
关键词:INS/GPS组合导航;Kalman滤波;预测残差;置信度
中图分类号:U666.1 文献标志码:A 文章编号:1672-7207(2011)S1-0436-05
Robust Kalman filter with confidence degree in INS/GPS integrated navigation
PAN Qian-xi, ZHAO Long, ZHANG Chang-yun
(National Key Laboratory of Science and Technology on Integrated Control Technology,
Beijing University of Aeronautics and Astronautics, Beijing 100191, China)
Abstract: In the situation of abnormal GPS signal in INS/GPS integrated navigation, a robust Kalman filter was designed. In this algorithm, prediction residual statistics is used to determine abnormal observations on the base of reliable motion model. Under a certain degree of confidence, when the exception was detected, the corresponding covariance matrix of observations was expanded. So the reliability of the measurements was reduced and the precision of the filter is improved. The simulation results prove that the algorithm is validity and reliability.
Key words: INS/GPS integrated navigaiton; Kalman filter; prediction residual error; degree of confidence
INS/GPS组合导航系统的数据融合一般采用Kalman滤波算法。传统的Kalman滤波在模型准确和系统先验信息已知的情况下能获得很好的精度,但在模型不准确和系统先验信息未知情况下,滤波精度会下降,甚至出现发散[1]。全球定位系统(GPS)可以提供全球、全天候、实时的高精度定位,但存在信号丢失和观测异常的情况[2]。此时,利用传统Kalman滤波实现INS/GPS组合导航信息融合时会导致系统精度下降,甚至发散。为了解决此问题,通常采用自适应滤波技术,在滤波的同时,抑制观测量中的异常值以提高滤波的精度。Sage等[3]提出了一种自适应滤波算法,可以在线计算系统噪声Q和量测噪声R。但实际上,Sage-Husa自适应滤波算法并不能同时将Q和R估计出来,而且张常云[4]已经证明了该算法只能在Q已知时估计出R,或R已知时估计出Q。沈云峰等[5]提出了一种简化的Sage-Husa自适应滤波算法,在已知Q的情况下,对R进行估计,该算法仍具有良好的自适应性,但由于每次滤波都估计R,滤波的复杂度增加,实际应用时,无法保证系统的实时性。国内外许多学者还研究了抗差滤波方法,该方法具有抑制观测异常的能力,目前研究较多的抗差估计理论主要有抗差最小二乘估计和抗差M估计[6]。观测量的权矩阵反映了各个观测量之间可信度的大小,抗差估计的实质在于等价权矩阵的构造。等价权包含了联合抗差的概念,对正常观测量采用保权处理,对于非正常但又可利用的观测量采用降权处理,对于粗差使其权为0,予以淘汰。等价权的构造方法有多种,如丹麦法权函数、Huber权函数和IGG Ⅲ方案权函数[7]。但无论是抗差最小二乘估计还是抗差M估计,均要求观测的法方程式满秩且有多余观测量。从抗差解的表达式 (其中A是观测阵,
(其中A是观测阵,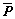 是等价权矩阵,L是观测向量)可以看出,当A满秩才能通过正常逆求得参数解向量[8]。而在一般的INS/GPS组合系统中,GPS只能提供3位置和3速度,共6维的观测量。而惯导/GPS组合导航系统的状态量要多于6个量,因此导致
是等价权矩阵,L是观测向量)可以看出,当A满秩才能通过正常逆求得参数解向量[8]。而在一般的INS/GPS组合系统中,GPS只能提供3位置和3速度,共6维的观测量。而惯导/GPS组合导航系统的状态量要多于6个量,因此导致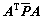 秩亏,无法进行参数的抗差估计。对于秩亏模型的抗差估计目前的研究还不多见,杨元 喜[9]通过分解观测矩阵和增加约束方程得到伪逆抗差解,该方法要求观测相关,但GPS的位置和速度等信息是独立观测量,因此该方法并不适用。杨元喜[8]已证明了等价权模型和方差膨胀模型之间的等价性,方差膨胀模型可以看作等价权模型的逆。因此,本文作者借鉴等价权函数的思想,利用观测向量协方差阵作为观测精度的评定指标,建立一个统计假设检验来检验滤波是否有异常。在给定置信度α下,利用假设检验如果未发现滤波异常,则观测协方差阵保持不变;反之,发现滤波异常,则构造方差膨胀函数,从而抑制观测误差对导航参数解的影响,更多地利用动力学模型的信息,提高了滤波精度,保证系统的可靠性。
秩亏,无法进行参数的抗差估计。对于秩亏模型的抗差估计目前的研究还不多见,杨元 喜[9]通过分解观测矩阵和增加约束方程得到伪逆抗差解,该方法要求观测相关,但GPS的位置和速度等信息是独立观测量,因此该方法并不适用。杨元喜[8]已证明了等价权模型和方差膨胀模型之间的等价性,方差膨胀模型可以看作等价权模型的逆。因此,本文作者借鉴等价权函数的思想,利用观测向量协方差阵作为观测精度的评定指标,建立一个统计假设检验来检验滤波是否有异常。在给定置信度α下,利用假设检验如果未发现滤波异常,则观测协方差阵保持不变;反之,发现滤波异常,则构造方差膨胀函数,从而抑制观测误差对导航参数解的影响,更多地利用动力学模型的信息,提高了滤波精度,保证系统的可靠性。
1 INS/GPS组合导航系统数学模型
1.1 系统方程
INS/GPS组合导航系统采用松组合方式,其中惯导系统采用平台式指北方位系统,在东北天坐标系下,取惯导系统的误差为组合系统的状态,即
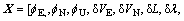
 (1)
(1)
其中: ,
, ,
, 为惯导平台误差角;
为惯导平台误差角;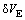 和
和 和
和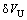 为惯导速度误差;
为惯导速度误差; ,
, 和
和 为惯导位置误差;
为惯导位置误差;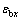 ,
, ,
, 为惯导系统陀螺漂移;
为惯导系统陀螺漂移; ,
, 和
和 为加速度计误差。
为加速度计误差。
设加速度计误差为一阶马尔科夫过程,设惯导陀螺漂移误差模型为
 (2)
(2)
其中:εb为陀螺常值漂移;εr为一阶马尔科夫过程;wg为白噪声。则系统状态方程为:
 (3)
(3)
离散化以后即为:
 (4)
(4)
其中, 和
和 分别为系统状态转移矩阵和系统噪声转移矩阵,具体形式见文献[10]。
分别为系统状态转移矩阵和系统噪声转移矩阵,具体形式见文献[10]。
1.2 量测方程
取惯导系统输出的位置和速度分别与GPS输出的位置和速度间的差值为观测向量(取三维位置和二维速度)
 (5)
(5)
其中:Ak为量测矩阵;Vk为量测噪声;Vk和Wk不相关,且满足
 ,
,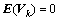
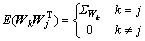
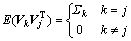
2 异常观测检测与观测协方差膨胀
2.1 异常观测检验
在模型检验过程中,预测残差起着非常重要的作用。预测残差定义为实际的系统输出与基于预测状态的系统输出之差,即
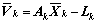 (6)
(6)
其中, 。
。
基于Kalman滤波的先验假设,若观测误差服从正态分布,则预测残差也服从零期望的正态分布[11],其协方差矩阵为
 (7)
(7)
构造如下统计量:
 (8)
(8)
 (9)
(9)
若H0假设成立,则模型有效,即认为GPS未发生观测误差;若H0假设不成立且假定动力学模型可靠,则状态预测向量 可靠,因此预测残差向量
可靠,因此预测残差向量 反映了观测分量
反映了观测分量 的误差,由于GPS观测分量彼此间相互独立,把统计量
的误差,由于GPS观测分量彼此间相互独立,把统计量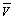 变换成标准的正态分布,按分量的形式可表示成
变换成标准的正态分布,按分量的形式可表示成
 (10)
(10)
式中: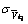 为预测残差的标准差,
为预测残差的标准差,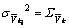 。设置信度为α,若在(1-α%)的置信水平上,由式(10)构成的统计量未超限,则表示
。设置信度为α,若在(1-α%)的置信水平上,由式(10)构成的统计量未超限,则表示 无异常。
无异常。
2.2 观测协方差膨胀
观测向量的协方差阵作为观测量精度评定指标应可靠地反映其离散程度。若观测精度高,可靠性好,则方差应该小,从而该观测值在状态估计中的权值就重;反之,则观测方差阵增大,使其在状态估计中的权重降低。在置信度为α时检测到观测有异常后,通过适当扩大异常观测的方差,以降低异常观测对参数估值的影响,更多地利用动力学模型的信息,提高参数估值的精度。如果GPS观测分量之间相对独立,可以对各个分量分别膨胀;反之,观测相关,则异常观测的方差膨胀应考虑与其相关联的协方差元素的调整,以使其膨胀后的方差和协方差仍保持原有的相关系数不变[8]。
方差膨胀因子函数有多种取法。文献[8]证明了方差膨胀模型和等价权模型之间的等价性,因此方差膨胀函数可取为等价权函数的倒数,如Huber权函数的倒数,IGGⅢ权函数的倒数等。当等价权函数存在0值时,此时方差膨胀因子应为∞,实际计算时用一个较大的正数替代。
根据IGGⅢ等价权函数模型,取三段方差膨胀函数为
 (11)
(11)
式中:k0和k1为常量,通常选k0=1.0~1.5,k1=2.5~8.0[12],设膨胀前观测协方差阵为 ,则膨胀后协方差变为
,则膨胀后协方差变为 。
。
3 计算与比较
在INS/GPS仿真实验时,用GSS公司STR系列星座模拟器进行运动轨迹的设定,并产生相应的星历射频(RF)信号。星座模拟器所模拟和输出的信号是GPS每颗导航卫星的模拟射频星历信号,用真实YP-4型GPS接收机进行数据采集。
本文取陀螺漂移速度为0.01(°)/h,加速度计漂移为10-5 g,正常时GPS的位置误差为5 m,速度误差为0.1 m/s。设定一条时间跨度1 000 s的匀速飞行过程用于算法仿真,其中在200~250 s和600~650 s的时间段内对GPS可见星中的一颗关键星加入50 m的伪距误差。限于星座模拟器给出的卫星伪距误差模型,实际施加的误差由前后两端斜坡和中间一段常值模型共3段组成,如图1所示。
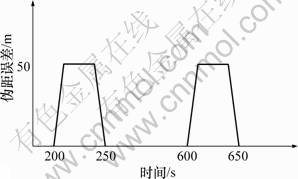
图1 对关键星施加的伪距
Fig.1 Pseudorange exerted on key satellite
利用上述实验数据进行验证,验证方案取以下3种:
方案(1):标准Kalman滤波解算;
方案(2):抗差Kalman滤波解算(置信水平α=0.2);
方案(3):抗差Kalman滤波解算(置信水平α=0.05)。
用上述3种方案进行滤波,速度和位置的滤波结果与参考真值的差值分别如图2~5所示,均方根误差比较见表1。
基于上述计算结果,可以看出:
(1) 由方案(1)的曲线可知,当GPS信号正常时,能够向惯导系统提供准确的观测信息,经过Kalman滤波后得到精度较高的状态估值,但是一旦GPS观测异常,则会立即污染滤波器导致状态估计错误。
(2) 由方案(1)和方案(2)比较可知,GPS的观测异常对常规Kalman滤波有明显的影响,而抗差Kalman滤波能够有效抵制观测异常对状态估计的影响。
(3) 由方案(2)和方案(3)比较可知,抗差Kalman滤波的效果与置信水平α有关,α影响对观测异常的检验,随着置信度的增大,滤波的均方根误差减小。
(4) 比较3个方案可知,抗差滤波的效果体现在观测发生异常的时间段,在观测正常的时刻,3种方案的滤波精度相同。
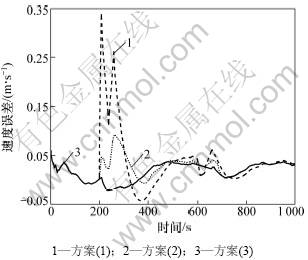
图2 3种方案的东向速度误差比较
Fig.2 East velocity error of three scheme
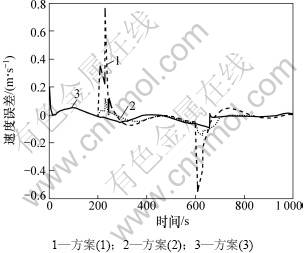
图3 3种方案的北向速度误差比较
Fig.3 North velocity errors of three schemes
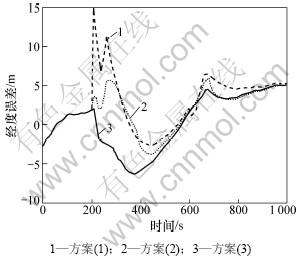
图4 3种方案的经度误差比较
Fig.4 longitude errors of three schemes
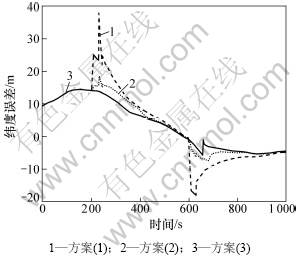
图5 3种方案的纬度误差比较
Fig.5 latitude errors of three schemes
表1 3种方案的误差均方根比较
Table 1 RMS errors of three schemes

4 结论
在传统Kalman滤波下,GPS观测异常会污染滤波器得出错误的估值。本文设计的抗差Kalman滤波通过异常观测的方差膨胀模型,更多地利用相对准确的动力学模型信息,以降低异常观测在参数估值中的权重,从而抵制其对参数估值的不利影响。异常观测的检验采用预测残差的统计模型,设立一个置信水平来判断观测是否出现异常,当发生异常时,根据预测残差的大小来构造方差膨胀模型。该算法合理地平衡了动力学模型和观测信息之间的权值,计算量不大,有效地提高了观测异常时的INS/GPS组合导航精度。
参考文献:
[1] 秦永元, 张洪钺, 汪叔华. 卡尔曼滤波与组合导航原理[M]. 西安: 西北工业大学出版社, 1998: 5-15.
QIN Yong-yuan, ZHANG Hong-yue, WANG Shu-hua. Kalman filter and theory of integrated navigation[M]. Xi’an: Northwestern Polytechnical University Press, 1998: 5-15.
[2] 王惠南. GPS导航原理与应用[M]. 北京:科学出版社, 2003: 10-35.
WANG Hui-nan. Theory and application of GPS navigation[M]. Beijing: Science Press, 2003: 10-35.
[3] Sage A P, Husa G W. Adaptive filtering with unknown prior statistics[C]//Proceedings of Joint Automatic Control Conference. Boulder, 1969: 760-769.
[4] 张常云. 自适应滤波方法研究[J]. 航空学报, 1998, 19(7): 96-99.
ZHANG Chang-yun. Approach to adaptive filtering algorithm[J]. Journal of Aeronautics, 1998, 19(7): 96-99.
[5] 沈云峰, 朱海. 简化的Sage-Husa自适应滤波算法在组合导航中的应用与仿真[J]. 青岛大学学报, 2001, 16(1): 44--50.
SHEN Yun-feng, ZHU hai. Application and simulation of simplified Sage-Husa adaptive Filter in integrated navigation system[J]. Journal of Qingdao University Engineering & Technology Edition. 2001, 16(1): 44-50.
[6] CUI X, Yang Y. Adaptively robust filtering with classified adaptive factors[J]. Progress in Natural Science, 2006, 16(8): 846-851.
[7] 宋迎春. 抗差自适应滤波中带有置信度的自适应因子设计[C]//第一届中国卫星导航学术年会论文集. 北京, 2010: 1-8.
SONG Ying-chun. Design of adaptive factor with confidence degree in robust adaptive filter[C]//Proceedings of CSNC2010, Beijing, 2010: 1-8.
[8] 杨元喜. 自适应动态导航定位[M]. 北京: 测绘出版社, 2006: 10-40.
YANG Yuan-xi. Adaptive navigation and kinematic positioning[M]. Beijing: Surveying and Mapping Press, 2006: 10-40.
[9] 杨元喜. 秩亏抗差最小二乘估计原理[J]. 测绘学报, 1994(5): 34-36.
YANG Yuan-xi. Rank eleficiency robust least squares estimation theory[J]. Bulletin of Surveying and Mapping, 1994(5): 34-36.
[10] 袁信, 俞济祥, 陈哲. 导航系统[M]. 北京: 航空工业出版社, 1993: 178-183.
YUAN Xin, YU Ji-xiang, CHEN Zhe. Navigation system[M]. Beijing: Aviation Industry Press, 1993: 178-183.
[11] 张斌. 基于BDS的惯性/卫星组合导航技术研究[D]. 北京: 北京航空航天大学自动化科学与电气工程学院, 2005: 40-42.
ZHANG Bin. Research of BDS-based inertial/satellite navigation technology[D]. Beijing: BUAA. School of Automation Science and Electrical Engineering, 2005: 40-42.
[12] 高为广. 基于当前加速度模型的抗差自适应Kalman滤波[J]. 测绘学报, 2005, 34(1): 15-18.
GAO Wei-guang. Adaptive robust kalman filtering based on the current statistical model[J]. Acta Geodaetica et Cartographica Sinica, 2005, 34(1): 15-18.
(编辑 赵俊)
收稿日期:2011-04-15;修回日期:2011-06-15
基金项目:航空基础科学基金资助项目(20100851018)
通信作者:赵龙(1976-),男,内蒙古赤峰人,副教授,从事组合导航和景象匹配研究;电话:13520191028;E-mail:flylong@buaa.edu.cn