Experimental study on magnetomechanical coupling effect of Q235 steel tubular member specimens

XIONG Er-gang(熊二刚)¹, WANG She-liang(王社良)², ZHANG Jun-feng(张俊峰)³, ZHANG Qian(张 倩)⁴

1. College of Civil Engineering, Chang’an University, Xi’an 710061, China;

2. School of Civil Engineering, Xi’an University of Architecture and Technology, Xi’an 710055, China;

3. School of Civil Engineering, Zhengzhou University, Zhengzhou 450001, China;

4. College of Civil Engineering, Xi’an Euraisa University, Xi’an 710065, China

Received 10 August 2009; accepted 15 September 2009

Abstract: The magnetomechanical coupling tests were performed on Q235 steel tubular model specimens in NIM-2000HF magnetomechanical coupling equipment. The hysteresis loops were obtained in different magnetic fields and stresses. The magnetization curves were also achieved at different stresses. The influence of applied stresses on the hysteresis loops was investigated. The stress sensitive region and linear stress sensitive region of magnetic induction are determined for the model specimen according to the experimental data. The linear dependence relation of magnetic induction versus applied stresses is established, and the optimum magnetic field is determined in the stress sensitive range of magnetic induction, which builds a basis for nondestructive testing (NDT) of stress with the total magnetic flux for steel structure.

Key words: magnetomechanical coupling tests; hysteresis loops; stress sensitive region; magnetic induction; total magnetic flux; nondestructive testing

It is well known that Q235 steel is not only one of the most widely used steels in engineering structures, but also belongs to a kind of ferromagnetic material. Naturally, Q235 steel reasonably exhibits a strong coupling of stress and microstructure with magnetic properties, which makes Q235 steel sensitive to magnetic field. In order to develop magnetic methods for nondestructive testing (NDT) of ferromagnetic materials and understand the involved physical mechanisms, many researches have been carried out in recent years[1-4]. Generally, these measurements were conducted under unloading conditions and the dependences of residual stress and microstructure on magnetic properties were widely studied[5-6]. However, the steel structural members in-service were sometimes under continuous external stress and hard to be dismantled from the whole structure. Therefore, an online measurement is indispensable. Recently, several works have been done to study the effect of uniaxial stress on magnetic Barkhausen noise (MBN) in steel under applied stress. KRAUSE et al[7] had performed an angular-dependent MBN measurement on pipeline steel under tensile stress, and GATELIER-ROTHEA et al[8] had studied the effects of uniaxial tensile and compressive stresses on MBN in carbon steel. In these works, the maximum loads were applied only up to the yield stress and significant differences between loading and unloading measurements have been reported. LIU et al[9] had established a clear relationship between the external stress and magnetic properties by two kinds of minor hysteresis loops methods are very applicable in the NDT of ferromagnetic materials. Several magnetic properties such as coercivity, hysteresis loss and permeability, which are sensitive to stress and microstructure changes, can be derived from the magnetic hysteresis loop[10-13].

Q235 steel of wide availability has been finding greater application in varieties of fields of national economic construction, so the defects or damages of steel members have ever been detected by the use of magnetic flux leakage in machinery and petroleum industries, etc. But those detections were focused on stress and strain concentrations, and defects, etc. Until now, especially in the field of civil engineering, it is rarely seen that the realtime stress of steel structural members is detected by the total magnetic flux and the dependence relation of magnetic induction versus the applied stresses was studied. In this work, the model specimens were fabricated from Q235 steel, the hysteresis loops were measured in this specimen under uniaxial tensile or compressive stress. The changes of hysteresis loops were studied in different stresses, the stress sensitive range of magnetic induction was found, the dependence relation of magnetic induction and stress was derived, which forms a certain basis for realtime online stress or damage testing of steel structural members with total magnetic flux.

2 Experimental

The Q235 steel tube was used in this experiment. The composition of Q235 steel is shown in Table 1. The model specimens and chucks are exhibited in Fig.1. The tubular specimens with 16 mm in outer diameter, 11 mm in inner diameter and 40 mm in length were held between the electromagnet poles.

Table 1 Composition of Q235 steel (w/%)

Fig.1 16 mm-diameter steel tubular model specimens and chucks

The schematic diagram of the experimental set-up is shown in Fig.2. The magnetomechanical coupling tester consists of a mechanical apparatus and a magnetic apparatus. The applied magnetic field is measured by a Hall sensor positioned on the specimen, the magnetic induction is measured by a pickup coil wound around the specimen, and the external force is applied along the long axis of the specimen by the mechanical loading device.

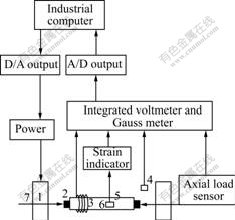
Fig.2 Schematic diagram of experimental set-up: 1—Electromagnet pole; 2—Loading collet; 3—Pickup coil; 4—Hall sensor; 5—Strain gauge; 6—Specimen; 7—Axial force

3 Results and discussion

The hysteresis loops of specimens under different stresses of -60, -40, -20, 0, 20, 40 and 60 MPa are shown in Fig.3. The measured hysteresis loops indicate that for a 16 mm-diameter steel tubular model, the stress sensitive region of magnetic induction starts from the nonlinear phase of magnetization curve, until the saturated phase of the magnetic induction still has certain sensitivity to the stress. Within the stress regions, the magnetic induction will ascend with the increase of tensile stress and decline with the increase of compressive stress, which reasonably reflects the main feature of the stress sensitivity of magnetic hysteresis loops.

The experimental results in Fig.3 can be explained by the magnetic domain theory[14] and turnover theory [15-16]. Due to the concurrent action of applied stress and magnetic field, the Q235 steel model specimen will not only experience an elastic strain, but a magnetostrictive strain, which will induce the movement of domain wall. As a consequence, for a Q235 steel with a positive magnetostriction, the application of tensile stress will rotate the magnetic induction along the direction of tensile stress, and the application of compressive stress will rotate the magnetic induction perpendicular to the compressive stress, which will make the tension direction become an easy magnetizing direction and the compression direction a difficult magnetizing direction.

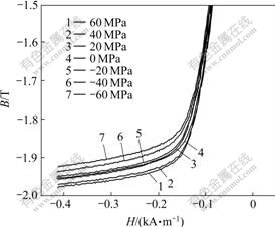
Fig.3 Comparison of B—H loops of model specimen under different applied stresses

Furthermore, from the aspect of energy, when a Q235 steel tubular specimen is subjected to the applied stresses, it will experience strain inside and stress will develop inside, which will lead to the changes in the magnetic permeability of steel. While being magnetized, if a steel specimen is constrained and unable to deform freely, the stress will develop inside. When a steel specimen expands due to magnetization thus to induce stress σ, the magnetoelastic energy E_σ must exist in steel. The analysis indicates that E_σ is proportional to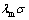, where λ_m is a magnetostrictive coefficient, and the energy E_σ is simultaneously related to the angle from the direction of magnetization to stress. The existence of E_σ will lead to the change of magnetization direction. For a positive magnetostrictive material, the tensile stress will rotate from the magnetization direction to the direction of tensile stress one, which will result in the increase of permeability along the tensile direction, and then cause the increase of magnetic induction; the compressive stress will make magnetization direction perpendicular to the stress, which will weaken the magnetization along the compressive stress, and thus reduce the permeability and magnetic induction. However, for a negative magnetostrictive material, the case is just on the contrary. This magnetized and stressed Q235 steel will produce magnetoelastic energy, this energy will reorient magnetization vector, and make magnetic induction vary with stresses.

Additionally, the results in Fig.3 indicate that the magnetic hysteretic loss of this specimen is very small, which further demonstrates that the Q235 steel model dissipates very little magnetic energy unlike Ni6 and Permalloy with an evident hysteresis loops[16-18].

4 Dependence relationship between magnetic induction and stress for Q235 steel member model

From the measured hysteresis loops, the magnetization curves with stresses are obtained as shown in Fig.4. Through the analysis and arrangement of experimental data, the stress sensitive region of Q235 steel tubular model specimen can be found, which will form a basis for magnetic nondestructive stress testing of steel structural members. The following deals with the magnetic induction of the model specimen at different applied stresses.

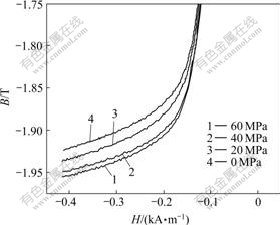
Fig.4 Magnetization curves under different tensile stresses

4.1 Tensile stress

The magnetization curve of the model specimen subjected to tensile stress is shown in Fig.4. From Fig.4, when the magnetic field H≤-0.05 kA/m, that is when the magnetization process reaches transition from the second phase to the third phase, the stress sensitivity of magnetic induction has been exhibited gradually, the magnetic induction increases with the increase of tensile stress, and their dependency relationship is approximately linear.

4.1.1 Determination of linear stress sensitive region of magnetic induction

The relationship between magnetic fields and tensile stress are shown in Fig.5.

From Fig.5, at the initial phase of magnetization curve, the effect of tensile stress on the magnetic induction is not stable and nonlinear. When H≤-0.25 kA/m, the magnetic induction just exhibits linear stress sensitivity, namely, with the increase of tensile stress, the magnetic induction increases at an approximate linearity. The values of magnetic induction are shown in Table 2 when the model specimen is subjected to an identical magnetic field but to different stresses, or when it is subjected to an identical stress but to different magnetic fields.

4.1.2 Linear fitting of magnetic induction and stress

According to the experimental data in Table 2, the least square method is utilized to fit the relation of magnetic induction versus stress. The resulting fitting equations are shown in Table 3.

From Table 3, when the applied magnetic field selected is equal to -0.40 kA/m, the standard deviation of fitting is the minimum; as a result, at the time of stress testing with total magnetic flux, the fitting equation corresponding to H= -0.40 kA/m can be considered the optimal fitting equation. While testing, the applied magnetic field is limited to H≤-0.15 kA/m.

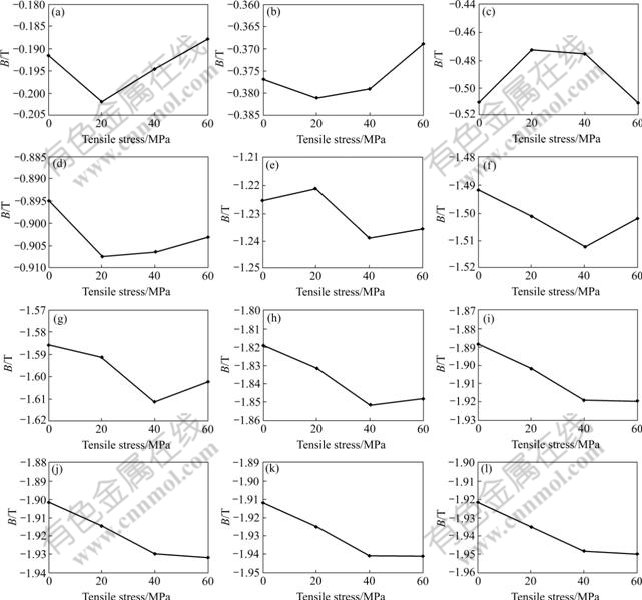
Fig.5 Relationship between tensile stress and magnetic induction at different magnetic fields: (a) 0.01 kA/m; (b) -0.02 kA/m;      (c) -0.03 kA/m; (d) -0.05 kA/m; (e) -0.07 kA/m; (f) -0.09 kA/m; (g) -0.10 kA/m; (h) -0.15 kA/m; (i) -0.25 kA/m; (j) -0.30 kA/m; (k) -0.35 kA/m; (l) -0.40 kA/m

Table 2 Values of magnetic induction at different magnetic fields and stresses (B/T)

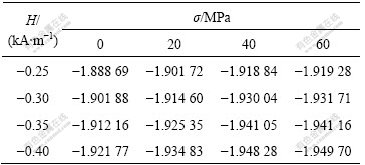
Table 3 Fitting equations of magnetic induction and stress at different magnetic fields

4.2 Compressive stress

The magnetization curve of the model specimen subjected to compressive stress is shown in Fig.6. From Fig.6, when the magnetic field H≤-0.06 kA/m, that is when the magnetization process reaches transition from the second phase to the third phase, the stress sensitivity of magnetic induction has been exhibited gradually, the magnetic induction increases with the increase of tensile stress, and their dependency relationship tends to be linear.

4.2.1 Determination of linear stress sensitive region of magnetic induction

The relations of different magnetic fields and compressive stress are shown in Fig.7.

From Fig.7, at the initial phase of magnetization curve, the effect of tensile stress on the magnetic induction

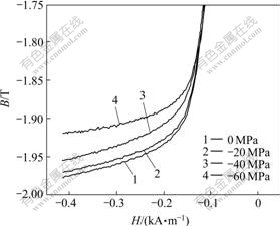
Fig.6 Magnetization curves under different compressive stresses

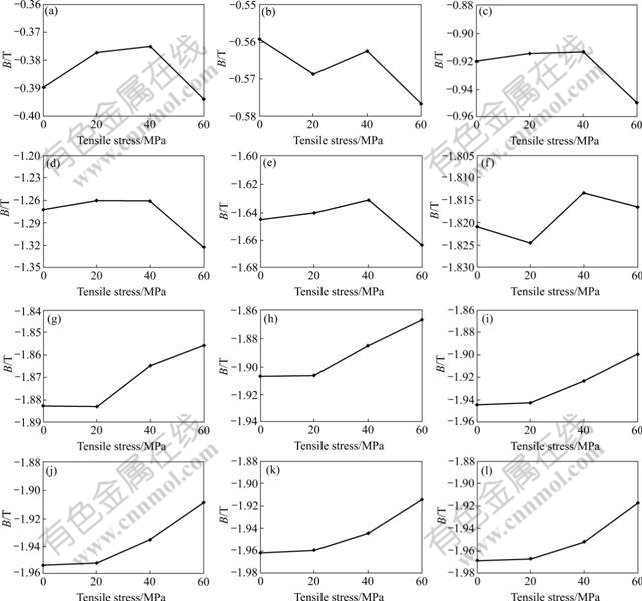
Fig.7 Relationship between compressive stress and magnetic induction at different magnetic fields: (a) -0.02 kA/m; (b) -0.03 kA/m; (c) -0.05 kA/m; (d) -0.07 kA/m; (e) -0.10 kA/m; (f) -0.13 kA/m; (g) -0.15 kA/m; (h) -0.20 kA/m; (i) -0.25 kA/m; (j) -0.30 kA/m; (k) -0.35 kA/m; (l) -0.40 kA/m

is not stable and nonlinear. When H≤-0.20 kA/m, the magnetic induction just exhibits linear stress sensitivity, namely with the increase of compressive stress, the magnetic induction decreases at an approximate linearity.

4.2.2 Linear fitting of magnetic induction and stress

Likewise, according to the experimental data, the least square method is utilized to fit the relationship between magnetic induction and stress. The resulting fitting equations are shown in Table 4.

Table 4 Fitting equations of magnetic induction and stress at different magnetic fields

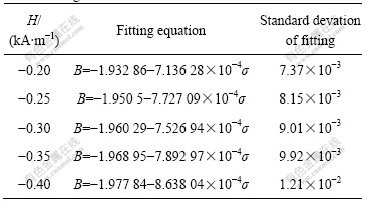
From Table 4, when the applied magnetic field selected is equal to -0.20 kA/m, the standard deviation of fitting is the minimum; as a result, at the time of stress testing with total magnetic flux, the fitting equation corresponding to H=-0.20 kA/m can be taken as the optimum fitting equation. While testing, the magnetic field of applicability ranges within H≤-0.15 kA/m.

5 Conclusions

1) A specially designed magnetomechanical tester was utilized to measure the magnetomechanical response of steel tubular specimens under different tensile and compressive stresses. The experimental results indicate that the stress sensitive region of magnetic induction for 16 mm diameter specimens equally falls in the phases of saturation magnetization and nonlinear magnetization; the stress sensitive region of magnetic induction is characterized by that the magnetic induction increases with the increase of tensile stress while the magnetic induction decreases with the increase of compressive stress and that the relationship of magnetic induction and stress approximates linear relationship. The simple relationship is of great applicability in NDT of steel structure.

2) The coercivity of the model specimen is quite small, which accounts for the small loss of magnetic hysteresis, that is to say, the steel model specimen possesses a stable magnetomechanical behavior, which can contribute to the convenient application to engineering.

References

[1] TAKAHASHI S, ECHIGOYA J, MOTOKI Z. Magnetization curves of plastically deformed Fe metals and alloys [J]. J Appl Phys, 2000, 87(2): 805-813.

[2] LIU T, KIKUCHI H, KAMADA Y, ARA K, KOBAYASHI S, TAKAHASHI S. Comprehensive analysis of Barkhausen noise properties in the cold rolled mild steel [J]. J Magn Magn Mater, 2007, 310(2): 989-991.

[3] STEWART D M, STEVENS K J, KAISER A B. Magnetic Barkhausen noise analysis of stress in steel [J]. Current Appl Phys, 2004, 4(2): 308-311.

[4] SAGAR S P, KUMAR B R, DOBMANN G, BHATTACHARYA D K. Magnetic characterization of cold rolled and aged AISI 304 stainless steel [J]. NDT & E Int, 2005, 38(8): 674-681.

[5] KLEBER X, VINCENT A. On the role of residual internal stresses and dislocations on Barkhausen noise in plastically deformed steel [J]. NDT & E Int, 2004, 37(6): 439-445.

[6] ZUREK Z H. Magnetic contactless detection of stress distribution and assembly defects in constructional steel element [J]. NDT & E Int, 2005, 38(7): 589-595.

[7] KRAUSE T W, PATTANTYUS A, ATHERTON D L. Investigation of strain dependent magnetic Barkhausen noise in steel [J]. IEEE Trans Magn, 1995, 31(6): 3376-3378.

[8] GATELIER-ROTHEA C, CHICOIS J, FOUGERES R, FLEISCHMANN P. Characterization of pure iron and (130 ppm) carbon-iron binary alloy by Barkhausen noise measurements: Study of the influence of stress and microstructure [J]. Acta Mater, 1998, 46(14): 4873-4882.

[9] LIU T, KIKUCHI H, ARA K, KAMAD Y, TAKAHASHI S. Magnetomechanical effect of low carbon steel studied by two kinds of magnetic minor hysteresis loops [J]. NDT & E Int, 2006, 39(5): 408-413.

[10] TAKAHASHI S, ZHANG L, KOBAYASHI Y, KAMADA Y, KIKUCHI H, ARA K. Analysis of minor hysteresis loops in plastically deformed low carbon steel [J]. J Appl Phys, 2005, 98(3): 1-8.

[11] V?RTESY G, M?SZ?ROS I, TOM?? I. Nondestructive indication of plastic deformation of cold-rolled stainless steel by magnetic minor hysteresis loops measurement [J]. J Magn Magn Mater, 2005, 285(3): 335-342.

[12] TAKAHASHI S, ZHANG L, KAMADA Y, KIKUCHI H, ARA K. A new analysis of minor hysteresis loops and QNDE [C]//AIP Conf Proc 2004. New York, 2004, 760: 1277-1284.

[13] TAKAHASHI S, KOBAYASHI S, KAMADA Y, KIKUCHI H, ZHANG L, ARA K. Analysis of minor hysteresis loops and dislocations in Fe [J]. Phys B: Cond Matter, 2006, 372(1/2): 190-193.

[14] JIANG S T, LI W. Magnetic physics of condensed matter [M]. Beijing: Science Press, 2003. (in Chinese)

[15] ZHU B, LO C CH, LEE S J. Micromagnetic modeling of the effects of stress on magnetic properties [J]. J Appl Phys, 2001, 89(11): 7009-7011

[16] FENG X. Studies on the constitutive theory and experiment of ferromagnetic materials [D]. Beijing: Tsinghua University, 2002. (in Chinese)

[17] FANG D N., FENG X, HWANG K C. Study of magnetomechanical non-linear deformation of ferromagnetic materials: Theory and experiment [C]//Proc Instn Mech Engrs. London, 2004: 1405-1410

[18] ERCUTA A, MIHALCA I. Magnetomechanical damping and magnetoelastic hysteresis in permalloy [J]. J Phys D: Appl Phys, 2002, 35(22): 2902-2908.

(Edited by ZHAO Jun)

Foundation item: Project(90715003) supported by the Major Program of National Natural Science Foundation of China; Project(09JS022) supported by Key Laboratory Research Project of Shaanxi Province Education Department, China; Project(09JS023, 09JS024) supported by Key Laboratory of Visiting Scholar Project of Shaanxi Province Education Department, China

Corresponding author: XIONG Er-gang; Tel: +86-13992846804; E-mail: x-e-g@163.com