An extended iterative direct-forcing immersed boundary method in thermo-fluid problems with Dirichlet or Neumann boundary conditions
来源期刊:中南大学学报(英文版)2017年第1期
论文作者:Ali Akbar Hosseinjani Ali Ashrafizadeh
文章页码:137 - 154
Key words:immersed boundary method; direct forcing; thermo-fluid problems; neumann boundary condition
Abstract: An iterative direct-forcing immersed boundary method is extended and used to solve convection heat transfer problems. The pressure, momentum source, and heat source at immersed boundary points are calculated simultaneously to achieve the best coupling. Solutions of convection heat transfer problems with both Dirichlet and Neumann boundary conditions are presented. Two approaches for the implementation of Neumann boundary condition, i.e. direct and indirect methods, are introduced and compared in terms of accuracy and computational efficiency. Validation test cases include forced convection on a heated cylinder in an unbounded flow field and mixed convection around a circular body in a lid-driven cavity. Furthermore, the proposed method is applied to study the mixed convection around a heated rotating cylinder in a square enclosure with both iso-heat flux and iso-thermal boundary conditions. Computational results show that the order of accuracy of the indirect method is less than the direct method. However, the indirect method takes less computational time both in terms of the implementation of the boundary condition and the post processing time required to compute the heat transfer variables such as the Nusselt number. It is concluded that the iterative direct-forcing immersed boundary method is a powerful technique for the solution of convection heat transfer problems with stationary/moving boundaries and various boundary conditions.
J. Cent. South Univ. (2017) 24: 137-154
DOI: 10.1007/s11771-017-3416-x
Ali Akbar Hosseinjani, Ali Ashrafizadeh
Faculty of Mechanical Engineering, K. N. Toosi University of Technology, P.O.B. 19395-1999 Tehran, Iran
 Central South University Press and Springer-Verlag Berlin Heidelberg 2017
Central South University Press and Springer-Verlag Berlin Heidelberg 2017
Abstract: An iterative direct-forcing immersed boundary method is extended and used to solve convection heat transfer problems. The pressure, momentum source, and heat source at immersed boundary points are calculated simultaneously to achieve the best coupling. Solutions of convection heat transfer problems with both Dirichlet and Neumann boundary conditions are presented. Two approaches for the implementation of Neumann boundary condition, i.e. direct and indirect methods, are introduced and compared in terms of accuracy and computational efficiency. Validation test cases include forced convection on a heated cylinder in an unbounded flow field and mixed convection around a circular body in a lid-driven cavity. Furthermore, the proposed method is applied to study the mixed convection around a heated rotating cylinder in a square enclosure with both iso-heat flux and iso-thermal boundary conditions. Computational results show that the order of accuracy of the indirect method is less than the direct method. However, the indirect method takes less computational time both in terms of the implementation of the boundary condition and the post processing time required to compute the heat transfer variables such as the Nusselt number. It is concluded that the iterative direct-forcing immersed boundary method is a powerful technique for the solution of convection heat transfer problems with stationary/moving boundaries and various boundary conditions.
Key words: immersed boundary method; direct forcing; thermo-fluid problems; neumann boundary condition
1 Introduction
Numerical simulation of fluid flow and convection heat transfer problems is often an essential ingredient of the analysis and design of various industrial products. It is also used extensively in phenomenological studies. To develop and improve such vitally important numerical simulation tools, many attempts have been made to provide accurate and efficient computational methods capable of solving problems in geometrically complex domains with stationary or moving boundaries. It is often a challenge to acquire both computational efficiency and accuracy especially when the boundaries of the solution domain do not conform to an orthogonal coordinate system. Finite element, finite volume and hybrid algorithms are all among the well-known methods that have been developed and widely used in response to the inherent weakness of the traditional finite difference methods in handling complex geometries. Immersed boundary method is a modern elegant attempt to use the power of the traditional techniques and classical solution algorithms on body non-conforming grids.
The immersed boundary method has originally been proposed by PESKIN [1] for the analysis of the blood flow around moving elastic heart valves. In the Peskin’s method, also known as the continuous forcing approach, the effects of the boundary points on the flow are simulated by singular body forces imposed on the immersed boundary (IB) or Lagrangian points. These forces at the IB points (IB forces) are then transferred to a number of Cartesian or Eulerian (Eu) grid points by a smooth Dirac delta function and play the role of momentum sources at those computational nodes. The accuracy and ease of boundary condition implementation in all immersed boundary methods depend strongly on the calculation of the IB forces and the aforementioned momentum sources.
Several methods have been developed based on the Peskin’s original approach. GOLDSTEIN et al [2] proposd the feedback forcing scheme, in which the IB forces are obtained in a feedback loop. SAIKI and BIRINGEN [3] used a high order finite difference approach, instead of the spectral method employed by GOLDSTEIN et al [2], in the context of the feedback forcing method to simulate the flow past both stationary and moving circular cylinders. The numerical instability of the feedback forcing method in some problems is an undesirable feature of this family of immersed boundary methods.
MOHD-YUSOF [4] suggested an explicit imposition of the boundary conditions in an immersed boundary framework. In this direct forcing method, the IB forces are directly calculated from the boundary conditions inserted into the discrete governing equations. More specifically, the imposition of the force terms in the Navier-Stokes equations is carried out through the assignment of fluid velocities at some grid points. The conceptual simplicity, low computational cost, strong numerical stability and lack of adhoc coefficients in the numerical implementation, make the direct forcing method an attractive numerical solution approach among the immersed boundary methods. Therefore, many researchers and method developers have worked around the direct forcing approach. For example, interesting problems have been solved by FADLUN et al [5], BALARAS [6] and MITTAL et al [7], which show the flexibility and applicability of the direct forcing method in solving complex flow problems. Also, UHLMANN [8] presented a direct forcing immersed boundary method to investigate the particulate flow in a multi-phase system and incorporateed a finite difference scheme and the projection method in the solution algorithm. A regularized delta function is used by UHLMANN [8] to smoothly transfer flow variable between the Eu and IB points.
The idea of multi-direct forcing scheme was proposed by WANG et al [9] based on Uhlmann’s method to more accurately implement the no-slip boundary condition. Further improvement in the accuracy of the boundary condition implementation was obtained through the iterative direct forcing immersed boundary method proposed by JI et al [10]. Here, the body forces at IB points are updated within the pressure iterations. By simultaneously calculating the body force and pressure in the incompressible flow numerical solution algorithm, the boundary conditions are fully satisfied and an accurate divergence-free velocity field is obtained.
While immersed boundary methods have originally been developed to solve incompressible flow problems and the focus has mainly been towards the calculation of momentum exchange between the flow and moving or stationary boundaries immersed in the fluid, the basic philosophy of the method can also be extended and used to numerically model the convective heat exchange as well. Attempts in this application area have already been started and is currently in progress. For example, PAN [11] solved a number of forced and natural convection problems using an immersed boundary method. YOON et al [12] apply the immersed boundary method in a finite volume framework to analyze two dimensional laminar flow and heat transfer past a circular cylinder near a moving wall. WANG et al [13] proposed an immersed boundary method based on multi-direct heat source scheme to numerically model natural convection between concentric cylinders as well as forced convection around a stationary circular cylinder. KIM et al [14] employed the immersed boundary technique to study natural convection of heat between a hot circular cylinder and the cold outer boundaries of a square enclosure. MARK et al [15] presented an extended hybrid method to calculate the temperature field. A heat source, which is calculated using the Fourier’s law, is applied to couple the flow and heat transfer solvers in this method.
Broadly speaking, the schemes required to implement the Dirichlet boundary conditions in immersed boundary methods are now mature and well developed and it is possible to calculate iso-therms in a heat transfer problem satisfactorily. On the contrary, Neumann boundary conditions and the calculation of iso-fluxes have only been discussed in a limited number of publications. PACHECO et al [16] presented an immersed boundary finite volume method for the solution of a range of convection heat transfer problems with both Dirichlet and Neumann boundary conditions. A fractional-step method was implemented on non-staggered grids to solve the test cases by PACHECO et al [16]. ZHANG et al [17] presented an interpolation scheme to impose Neumann boundary condition on the body surface. They defined a layer of grid points near the immersed boundary and along the outward normal direction. Then, the normal derivative of temperature was approximated by the first order one-sided finite difference scheme, from which the wall temperature was computed. PAN [18] developed a ghost cell immersed boundary method, which is capable of handling both Neumann and Dirichlet boundary conditions. REN et al [19] proposed an efficient immersed boundary technique for thermal flow problems with Neumann boundary condition. They modeled the effects of thermal boundary conditions on the velocity and temperature fields via heat flux correction. In particular, heat sources/sinks are determined in such a way that the thermal boundary conditions are accurately satisfied.
In the present work, the iterative direct forcing immersed boundary method, proposed by JI et al [10], was extended and used to solve convection heat transfer problems. The momentum and the heat sources required to implement the boundary conditions at the IB points and also the pressure at grid points are calculated simultaneously in an iterative process at each time step. This approach improves the accuracy of the immersed boundary method with a computational cost comparable to non-iterative alternatives. Two direct and indirect implementation methods are employed to impose Neumann boundary condition and are compared in terms of the computational efficiency and accuracy. Free, forced and mixed convection heat transfer test cases in both bounded and unbounded domains, as well as stationary and moving boundaries, were solved to show the applicability and satisfactory performance of the method. Validation test cases included forced convection on a heated cylinder in an unbounded domain and mixed convection around a circular body in a lid-driven cavity. Furthermore, the proposed method was applied to study the mixed convection around a heated rotating cylinder in a square enclosure with both iso-heat flux and iso-thermal boundary conditions.
2 Governing equations and boundary conditions
The governing equations for an incompressible flow with heat convection in the computational domain Ω in the context of immersed boundary method are as follows:
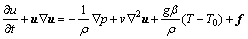 (1)
(1)
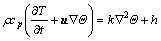 (2)
(2)
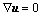 (3)
(3)
where u is the fluid velocity vector, p is the pressure, v is the kinematic viscosity and ρ is the density of the fluid. Also, β is the coefficient of thermal expansion, g is the gravitational acceleration, T is the temperature of the fluid, T0 is a reference temperature, cp is the fluid heat capacity and k is the coefficient of thermal conductivity of the fluid. In this set of equations, f is the external momentum source, used to impose the no-slip boundary condition, and h is the external heat source, added to the energy equation to implement the specified thermal boundary condition.
To cast the governing equations into a non- dimensional form, the following dimensionless variables are introduced:
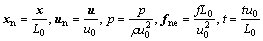 (4)
(4)
where u0 and L0 are the problem-dependent velocity and length scales, respectively. Depending on the problem and the given boundary conditions, one of the following definitions is used for the non-dimensional temperature:
 (5)
(5)
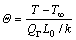 (6)
(6)
where TH and TC represent hot and cold reference temperatures respectively, QΓ is the specified non-zero heat flux at the boundary and T∞ is the far field temperature.
Substituting the above dimensionless variables into Eqs. (1)-(3) results in the following dimensionless forms of the governing equations:
 (7)
(7)
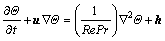 (8)
(8)
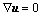 (9)
(9)
where f and h are non-dimensional sources and Re, Pr and Ra are the Reynolds, Prandtl, and Rayleigh numbers respectively defined as follows.
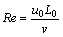 (10)
(10)
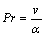 (11)
(11)
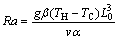 (12)
(12)
where α=k/ρcp is the thermal diffusivity.
Depending on the problem and the given boundary conditions, one of the following definitions is used for the non-dimensional thermal source:
 (13)
(13)
 (14)
(14)
The no-slip boundary condition requires the equality of the fluid and boundary velocities at the interface:
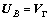 (15)
(15)
where VΓ is the non-dimensional boundary velocity and UB is the corresponding non-dimensional fluid velocity at the boundary.
Using the above definitions, Dirichlet and Neumann thermal boundary conditions are expressed as follows:
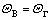 (16)
(16)
 (17)
(17)
In Eq. (16), ΘΓ is the non-dimensional boundary temperature and ΘB is the corresponding non- dimensional fluid temperature at the boundary. The non- dimensional normal temperature derivative at the boundary is shown by 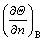 in Eq. (17).
in Eq. (17).
3 Boundary condition implementation
3.1 Immersed boundary treatment
Two operators, I(f) and D(Φ), are defined as suggested by JI et al [10] which represent the interpolation and distribution operators respectively. The parameter f represents variables such as u, p, f, Θ, h,  Θ/
Θ/ n at the uniformly-distributed Eu points, and the parameter Φ indicates the variables at IB point, i.e. U, P, F, Θ, H,
n at the uniformly-distributed Eu points, and the parameter Φ indicates the variables at IB point, i.e. U, P, F, Θ, H,  Θ/
Θ/ n. Note that an over bar is used to distinguish the non-dimensional temperature at a Lagrangian point from the non-dimensional temperature at an Eulerian point.
n. Note that an over bar is used to distinguish the non-dimensional temperature at a Lagrangian point from the non-dimensional temperature at an Eulerian point.
Using the interpolation operator, any variable at an IB point, i.e. Φ(XIB), can be expressed as follows:
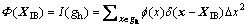 (18)
(18)
where gh represents a set of Cartesian grid points at both sides of the immersed boundary point XIB, here called the active grid points. In other words, Eq. (18) interpolates the values of a fluid variable at a limited number of Eu points (the active grid points) to assign a value to that variable at a boundary (IB) point. Coordinates XIB=(XIB, YIB) and xn=(x, y) represent IB and Eu points respectively and △x is the non-dimensional uniform Cartesian grid size.
The discrete delta function (△) is defined as follows [20]:
 (19)
(19)
with
 (20)
(20)
Likewise, using the distribution operator, any variable at an Eu point, i.e. f(x), can be expressed as follows:
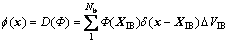 (21)
(21)
where Nb is the total number of boundary points and △VIB=△x×△SIB is the discrete volume (cell area in 2D) around the IB point as defined by UHLMANN [8] and △SIB is the distance between any two consecutive IB points. Once again, note that any variable at a boundary point is actually distributed over a limited number of cells around that particular IB point (active cells).
3.2 Calculation of momentum and heat sources
The non-dimensional momentum and energy equations are discretized to obtain the following evolution equations for the discrete values of fluid velocity and temperature as follows:
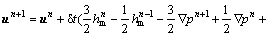
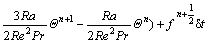 (22)
(22)
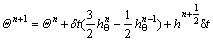 (23)
(23)
where variable hm includes momentum convection and diffusion, i.e. 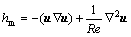 , and variable hΘ includes heat convection and diffusion, i.e. hΘ=
, and variable hΘ includes heat convection and diffusion, i.e. hΘ= 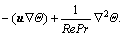 Unsteady convection, diffusion
Unsteady convection, diffusion
and pressure terms are treated by the second order Adams-Bashforth method and all space derivatives are discretized by the second order central difference scheme.
The following three types of boundary conditions are implemented in the present study.
1) No-slip boundary condition:
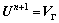 (24)
(24)
2) Thermal dirichlet boundary condition:
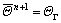 (25)
(25)
3) Thermal neumann boundary condition:
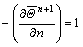 (26)
(26)
where Un+1 is the non-dimensional fluid velocity at an IB point, Θn+1 and 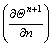 are non-dimensional fluid temperature and normal derivative of temperature at the IB point respectively as mentioned before. Using the interpolation operator, the boundary conditions can also be written as
are non-dimensional fluid temperature and normal derivative of temperature at the IB point respectively as mentioned before. Using the interpolation operator, the boundary conditions can also be written as
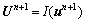 (27)
(27)
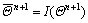 (28)
(28)
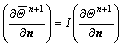 (29)
(29)
where un+1, Θn+1 and 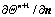 are the non-dimensional velocity, temperature and normal derivative of temperature at the Eu points respectively as explained before.
are the non-dimensional velocity, temperature and normal derivative of temperature at the Eu points respectively as explained before.
The intermediate temperature and velocity variables, i.e. Θ* and u, are now defined as follows:
 (30)
(30)
 (31)
(31)
By substituting Eqs. (24)-(26) into Eqs. (27)-(29) respectively, employing Eqs. (22)-(23) for un+1 and Θn+1, and using the intermediate variables just introduced, the following equations are obtained:
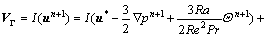
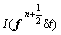 (32)
(32)
 (33)
(33)
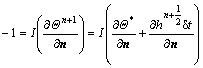 (34)
(34)
These equations can be rewritten as follows:
 (35)
(35)
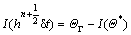 (36)
(36)
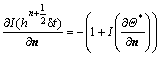 (37)
(37)
The momentum and heat sources at IB points, i.e. 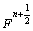 and
and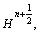 can now be expressed as
can now be expressed as 
 and
and 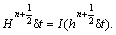
Using the distribution operator, the momentum sources at Eu points can now be calculated as follows:
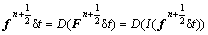
 (38)
(38)
These force terms (momentum sources) at Cartesian grid points, which are directly obtained from the specified velocity boundary conditions, are used to enforce the no-slip boundary condition in the immersed boundary method used in this work.
Similar expression can be obtained for 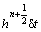 to implement Dirichlet and Neumann boundary conditions as explained below.
to implement Dirichlet and Neumann boundary conditions as explained below.
3.2.1 Dirichlet thermal boundary condition implementation
For the implementation of the Dirichlet boundary condition, the heat sources at Cartesian grid points can be simply calculated via the distribution operator as
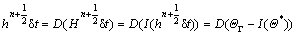 (39)
(39)
These heat sources at Eu points, which are directly obtained from the specified boundary temperature, are used to enforce the Dirichlet thermal boundary condition in the immersed boundary method used in this work.
3.2.2 Neumann thermal boundary condition implementation
Two methods for the implementation of Neumann boundary condition are introduced in this section.
In the first method, here called the indirect method, the Neumann boundary condition is imposed indirectly via the implementation of a suitably determined, or equivalent, Dirichlet boundary condition. This means that ΘΓ in Eq. (39) is first computed from the specified boundary heat flux and then the problem is solved as if the boundary temperatures have been specified originally. To compute ΘΓ using the specified boundary heat flux, a layer of virtual points are defined △x away from the boundary along the normal direction as shown in Fig. 1(a). To obtain the normal vector at an IB point, the method suggested by BALARAS [6] is applied. The boundary temperature can then be computed as

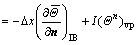 (40)
(40)
where I(Θn)vp is the virtual point temperature at the time step n, 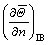 is the known normal derivative of temperature at the IB point, and
is the known normal derivative of temperature at the IB point, and 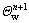 is the computed boundary temperature corresponding to the given Neumann boundary condition. A similar scheme has also been suggested by ZHANG et al [17] to impose the Neumann boundary condition.
is the computed boundary temperature corresponding to the given Neumann boundary condition. A similar scheme has also been suggested by ZHANG et al [17] to impose the Neumann boundary condition.
In the second method, here called the direct method, Eq. (37) can be used to obtain the heat sources at the Eu points as follows:
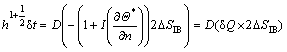 (41)
(41)
where the quantity  is the heat flux difference at the IB point and △SIB is the surface area corresponding to the IB point (Fig. 1(b)). Note that here the Neumann boundary conditions are directly employed to calculate the heat sources at Eulerian grid points. The details of how to obtain Eq. (41) form Eq. (37) is provided in the appendix A. Using a different approach, a similar equation is derived by REN et al [19] to impose Neumann boundary condition.
is the heat flux difference at the IB point and △SIB is the surface area corresponding to the IB point (Fig. 1(b)). Note that here the Neumann boundary conditions are directly employed to calculate the heat sources at Eulerian grid points. The details of how to obtain Eq. (41) form Eq. (37) is provided in the appendix A. Using a different approach, a similar equation is derived by REN et al [19] to impose Neumann boundary condition.
To calculate  at an IB point, the following expression is employed:
at an IB point, the following expression is employed:
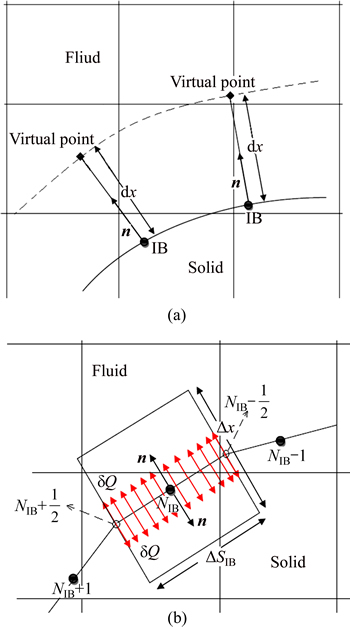
Fig. 1 Schematic virtual points and IB points for indirect implementation of Neumann boundary condition (a) and volume corresponding to an IB point and heat flux along two normal directions for direct implementation of Neumann boundary condition (b)
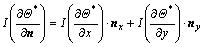 (42)
(42)
where 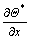 and
and 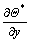 represent intermediate temperature derivatives with respect to x and y at the IB point, estimated using second order central difference scheme, and nx and ny are the components of the normal unit vector. With the expression for
represent intermediate temperature derivatives with respect to x and y at the IB point, estimated using second order central difference scheme, and nx and ny are the components of the normal unit vector. With the expression for  it is now possible to use Eq. (41) to calculate
it is now possible to use Eq. (41) to calculate 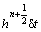 at the grid points and directly impose the Neumann boundary condition.
at the grid points and directly impose the Neumann boundary condition.
4 Numerical implementation
The main steps of the numerical solution algorithm at the time step n+1 are as follows:
1) Prediction step
Calculate the intermediate temperature Θ* and velocity u* from Eqs. (30) and (31).
2) The following outer iteration loop is carried out to calculate intermediate pressure, pn,k, momentum
source (body force), 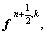 and the heat source,
and the heat source, 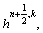 at the Eu points. Let pn,0=pn, Θn,0=Θn and k=1, note that k is the iteration number in the outer loop.
at the Eu points. Let pn,0=pn, Θn,0=Θn and k=1, note that k is the iteration number in the outer loop.
Outer loop begins:
a) Update 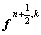 from Eq. (38) and
from Eq. (38) and 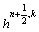 from Eq. (39) or (41) as discussed in Section 3.2. The velocity at the IB point will not be close enough to the assigned boundary velocity after one cycle of velocity interpolation and force distribution. Therefore, here the cycle is repeated 10 times as suggested by JI et al [10] in an inner iteration loop as follows (i is the numerator in the inner loop):
from Eq. (39) or (41) as discussed in Section 3.2. The velocity at the IB point will not be close enough to the assigned boundary velocity after one cycle of velocity interpolation and force distribution. Therefore, here the cycle is repeated 10 times as suggested by JI et al [10] in an inner iteration loop as follows (i is the numerator in the inner loop):
Inner loop begins
Let 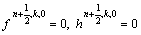 .
.
Do i=1:10

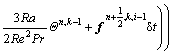 (43)
(43)
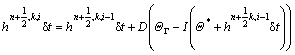 (44)
(44)
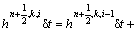
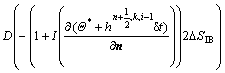 (45)
(45)
End Do
Let  and
and 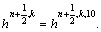
Note that one of Eqs. (44) and (45) is used in this algorithm, depending on the type of the specified boundary condition. For the Neumann boundary condition implementation via the indirect scheme, the boundary temperature computed by Eq. (40) is used as the boundary temperature (ΘΓ) in Eq. (44). For the direct implementation of the Neumann boundary condition, Eq. (45) is employed to compute the heat sources at Eu points.
b) Correct the calculated values of the intermediate velocity and temperature:
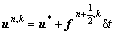 (46)
(46)
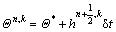 (47)
(47)
c) Update pressure:
 (48)
(48)
d) Check convergence using the following L2 norm:
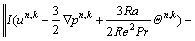
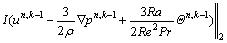 (49)
(49)
The parameter ε is user specified and determines the tolerable error. The value ε=10-4 is used in this work.
If the L2 norm is less than ε, go to step c), otherwise go to step e) of the outer loop.
e) Let k=k+1
End of the outer iteration loop.
3) Correction step
 (50)
(50)
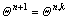 (51)
(51)
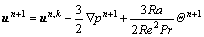 (52)
(52)
The pressure Poisson equation (PPE), Eq. (48), is solved by an iterative conjugate gradient (CG) method. A considerable amount of computational time can be saved by using approximate pressure values at the intermediate stages. Therefore, loose convergence of the PPE solver at the intermediate iterations is sufficient.
The proposed algorithm is summarized in the flowchart diagram shown in Fig. 2.
In the given flowchart, tMax is the non-dimensional transient solution time. Finite difference and staggered grids are used to discretize and solve the flow and heat transfer equations in this work. More details regarding the discretization are provided in the Appendix B.
5 Test cases
Three problems are now solved using the proposed iterative direct forcing method. These problems include:
1) Forced convection around a heated circular cylinder with a prescribed surface heat flux (Neumann boundary condition) in an unbounded domain;
2) Free and mixed convection around a circular cylinder with both Dirichlet and Neumann boundary conditions in a lid-driven cavity;
3) Free and mixed convection around a heated rotating circular cylinder with both Dirichlet and Neumann boundary conditions in a square enclosure.
5.1 Forced convection around a heated circular cylinder with Neumann boundary condition in an unbounded domain
In this test case, forced heat convection over a circular cylinder with diameter D placed in an unbounded uniform flow is considered. Neumann condition 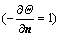 is given along the boundary of the stationary heated cylinder, centered at 8D from the inlet and 15D from the lower boundary. A sufficiently large computational domain (30D×30D) is employed for the numerical simulation. Upper and lower boundaries of the domain are assumed far enough so that boundary conditions
is given along the boundary of the stationary heated cylinder, centered at 8D from the inlet and 15D from the lower boundary. A sufficiently large computational domain (30D×30D) is employed for the numerical simulation. Upper and lower boundaries of the domain are assumed far enough so that boundary conditions  u/
u/ y=0 and
y=0 and  Θ/
Θ/ y=0 are employed at those outer boundaries. The inlet boundary conditions are u= (1, 0), Θ=Θ∞=0 and the boundary conditions at the outlet are
y=0 are employed at those outer boundaries. The inlet boundary conditions are u= (1, 0), Θ=Θ∞=0 and the boundary conditions at the outlet are  u/
u/ x=0,
x=0,  Θ/
Θ/ x=0. The computational results in this test case are obtained using a 3600×3600 uniform grid, which corresponds to △x=1/120. Grid refinement study is carried out with five different grids, i.e., △x=1/20, △x=1/40, △x=1/80, △x=1/120 and△x=1/240.
x=0. The computational results in this test case are obtained using a 3600×3600 uniform grid, which corresponds to △x=1/120. Grid refinement study is carried out with five different grids, i.e., △x=1/20, △x=1/40, △x=1/80, △x=1/120 and△x=1/240.
The results are obtained at four different Reynolds numbers, i.e. Re=10, 20, 40, 100 and a fixed Prandtl number (Pr=0.7), where Re and Pr are defined by Eqs. (10) and (11), respectively. Since buoyancy is not involved in this problem, the value of zero is assigned to the Rayleigh number. The velocity and length scales in Eq. (10) are defined as u0=1 m/s and L0=D, respectively. The indirect and direct methods for the implementation of the Neumann boundary condition, discussed in Section 3.2.2, are both employed to solve the problem in this test case.
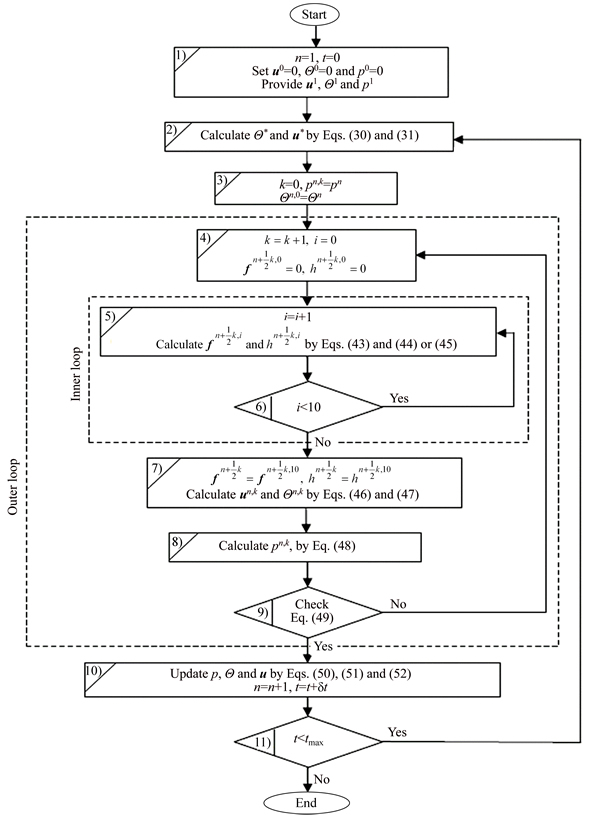
Fig. 2 Computational algorithm
Figure 3 shows the grid convergence study using the following L2 norm:
 (53)
(53)
In the above equations, N is the number of grid points and Θ is the temperature at the Eu points. The numerical solution on the computational grid with △x=1/240 is assumed exactly (i.e. Θfine) and the time step is chosen equal to △t=0.0001.
As shown in Fig. 3, the order of accuracy of the first (indirect) method is less than the order of accuracy in the second (direct) method, at least for the rather coarse grids. It is somewhat expected because, as mentioned before, a first order approximation is applied to discretize the Neumann boundary condition in the indirect method (scheme 1).

Fig. 3 Grid convergence study for the first test case
Figure 4 shows the streamlines for Re=20, 40 and 100 in this test case. A pair of symmetric eddies are formed behind the cylinder at Re=20 and Re=40 and unsteady Karman street is observed at Re=100. Note that the circular boundary is sharply captured and there is no any streamline penetration at the physical boundary. This is a reflection of the fact that both continuity and the no-slip boundary condition are fully satisfied. The isotherms around the cylinder are also shown in Fig. 5 for Re=20, 40 and 100. As expected, the temperature around the cylinder surface decreases faster at higher Reynolds numbers.
Figure 6 illustrates the variation of the local Nusselt number around the cylinder. Here, the angle θ is measured from the leading edge of the cylinder. The computational results in Fig. 6 are also compared to the results presented by BHARTI et al [21]. Excellent agreement is observed. The local Nusselt number at an IB point is calculated as follows:
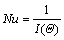 (54)
(54)

Fig. 4 Streamlines around circular cylinder for the first test case:
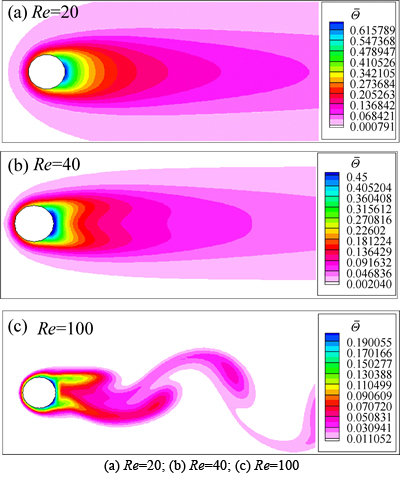
Fig. 5 Temperature field around circular cylinder for the first test case:

Fig. 6 Comparison of local Nusselt numbers along boundary for Re=10 and Re=20 (The second scheme in Neumann boundary condition implementation is applied here)
When the indirect scheme is employed, the temperature along the body surface is calculated as part of the solution procedure and the Nusselt number is obtained via Eq. (54). However, an additional computational time is required to calculate the Nusselt number when the direct scheme is used.
Table 1 compares the calculated average Nusselt numbers and drag coefficients at Re=10, 20, 40 via indirect and direct schemes with other reported results. Good agreement is evident for both methods. The average Nusselt number, Nu, and drag coefficient, CD, are defined as follows:
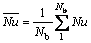 (55)
(55)
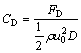 (56)
(56)
where FD is the drag force. Note that the direct and indirect methods provide similar drag coefficients, therefore, only the values obtained from the indirect method are reported in Table 1.
Table 1 Comparison of results obtained from indirect and direct methods with other available data

5.2 Mixed convection around a stationary circular cylinder in a lid-driven cavity
In the second example, also studied by KHANAFER and AITHAL [23], mixed convection heat transfer around a circular cylinder in a lid-driven cavity is considered. Both Dirichlet and Neumann boundary conditions are discussed in this case. The radius of the cylinder is r=0.2L, as shown in Fig. 7. The vertical walls of the cavity are adiabatic while the upper wall is maintained at a lower temperature (ΘC=0) compared to the bottom wall which is maintained at ΘH=1. Calculations have been carried out at four different
Richardson numbers 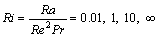 and a fixed Prandtl number Pr=0.7. The Rayleigh and Reynolds numbers are defined by Eqs. (10) and (12), respectively. The Reynolds number is fixed (Re=100) and different Richardson numbers are obtained by varying the Rayleigh number. Also, the non-dimensional temperature is defined by Eq. (5) and velocity and length scales are u0=1 m/s and L0=L respectively. In the case of Ri=∞, which is corresponding to the pure natural convection, Rayleigh number is fixed (Ra=105) and the velocity scale is u0=α/L. In the case of Neumann (adiabatic) boundary condition on the surface of the cylinder, the direct scheme, discussed in Section 3.2.2, is applied. Grid dependency study in this case is carried out and shown in Fig. 8. A 200×200 uniform Cartesian grid seems to be appropriate in this case. The results for the finest (400×400) grid, is used to conduct the convergence study. The time step in this case is equal to △t=0.0001.
and a fixed Prandtl number Pr=0.7. The Rayleigh and Reynolds numbers are defined by Eqs. (10) and (12), respectively. The Reynolds number is fixed (Re=100) and different Richardson numbers are obtained by varying the Rayleigh number. Also, the non-dimensional temperature is defined by Eq. (5) and velocity and length scales are u0=1 m/s and L0=L respectively. In the case of Ri=∞, which is corresponding to the pure natural convection, Rayleigh number is fixed (Ra=105) and the velocity scale is u0=α/L. In the case of Neumann (adiabatic) boundary condition on the surface of the cylinder, the direct scheme, discussed in Section 3.2.2, is applied. Grid dependency study in this case is carried out and shown in Fig. 8. A 200×200 uniform Cartesian grid seems to be appropriate in this case. The results for the finest (400×400) grid, is used to conduct the convergence study. The time step in this case is equal to △t=0.0001.

Fig. 7 Solution domain and other relevant information for the second test case
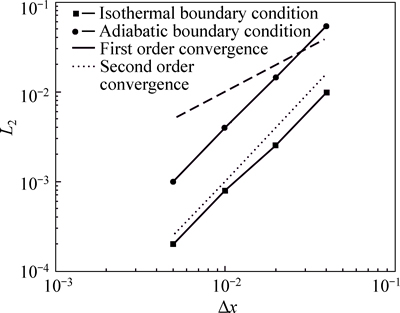
Fig. 8 Grid convergence study for the second test case
Figures 9 and 10 show the isotherms and stream function values corresponding to different flow regimes at Ri=0.01, 1, 10 and ∞ for both Dirichlet and Neumann boundary conditions, where xp and yp are the dimensions of cavity. The minimum and maximum values of the stream function are shown as Ψ=(Ψmin, Ψmax) at the top of the relevant color plots.
As expected, natural convection becomes more important at higher Richardson numbers. Also, it is seen that stronger natural convection leads to the enhancement of the buoyancy induced flow. The computed stream function values show that the difference between maximum and minimum values of stream function (△Ψ=Ψmax-Ψmin) increases with Richardson number. The rate of this increase in △Ψ for the adiabatic case is somewhat more than the isothermal case. Thermal shielding effect of the cylinder is observed in Figs. 9(a) and 10(a). Note that the results are not symmetric due to the movement of the cavity lid. However, symmetric flow and temperature fields around the cylinder are obtained for Ri=∞ as expected.
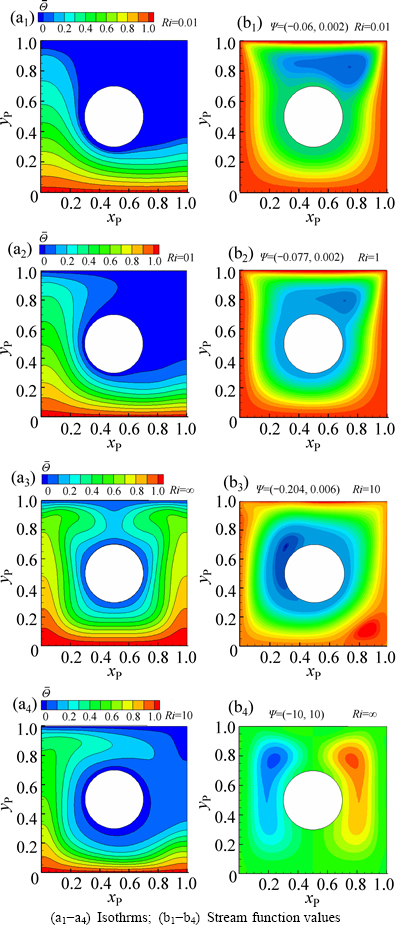
Fig. 9 Effect of isothermal cylinder on isotherms and stream function values for various Richardson numbers (Ri=0.01, 1, 10, ∞) in the second test case: (a1-a4) Isothrms; (b1-b4) Stream function values
Figures 11(a) and (b) show the effects of the Richardson number on the local Nusselt numbers measured along the isothermal and adiabatic cylinders respectively. The local Nusselt number at an IB point is defined by Eqs. (57) and (54) in the case of isothermal and adiabatic boundary condition respectively. Note thatΘ in Eq. (57) is defined according to Eq. (5). Excellent agreement with the results reported by KHANAFER et al [23] is observed.
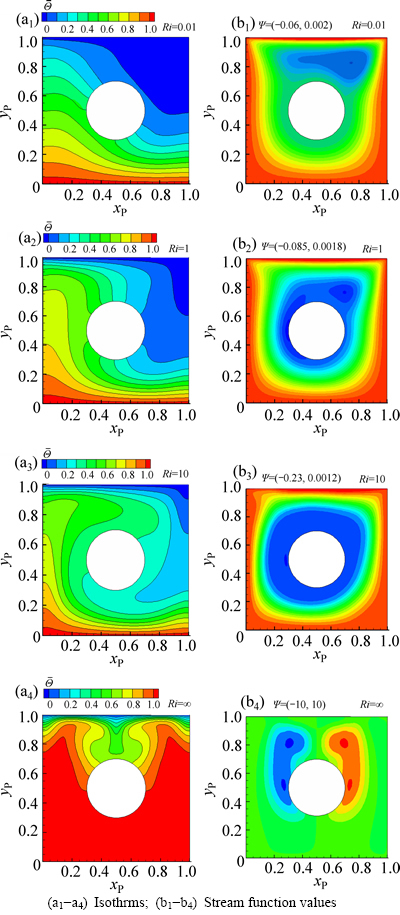
Fig. 10 Effect of adiabatic cylinder on isotherms and stream function values for various Richardson numbers (Ri=0.01, 1, 10, ∞) in the second test case: (a1-a4) Isothrms; (b1-b4) Stream function values
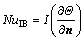 (57)
(57)
To calculate the Nusselt number, the following procedure is carried out. First virtual points, similar to the virtual points defined in the indirect scheme discussed in section 3.2.2, are defined. Then, the temperatures at the virtual points are calculated by the interpolation operator and, finally, the Nusselt number is calculated as follows:
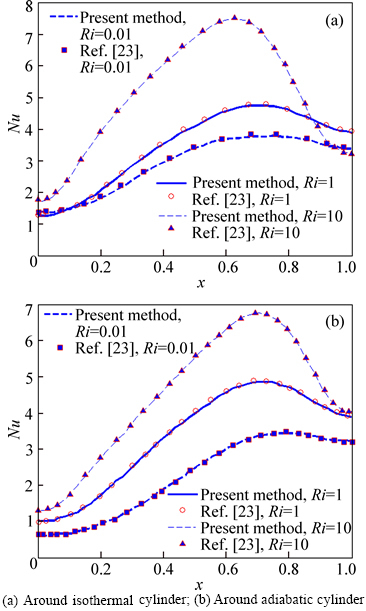
Fig. 11 Local Nusselt numbers around isothermal cylinder at Ri=0.01, 1, 10 for the second test case:
 (58)
(58)
where △x is the grid size, ΘΓ is the given wall temperature, and  is the interpolated temperature at the virtual point.
is the interpolated temperature at the virtual point.
Figures 12(a) and (b) show the effects of the Richardson number on the variation of temperature along a vertical line at x=0.15 and a horizontal line at y=0.15. Again, very good agreement with the results presented by KHANAFER and AITHAL [23] is observed. Note that the temperatures along those lines are higher for the adiabatic cylinder case regardless of the Richardson number value. The difference between the maximum and minimum temperatures decreases with the increase of the Richardson number.
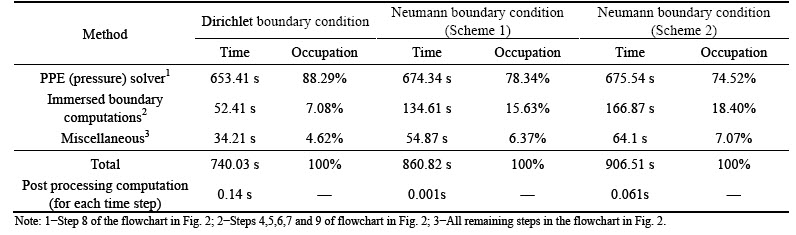
As mentioned before, some computations are required as pre-processing to impose Neumann boundary condition in both schemes discussed in Section 3.2.2. To have a sense of this additional computational cost, a comparison is provided in Table 2. The results are obtained using a PC computer with 4.0 GHz clock speed, 8 GB RAM, and an eight-core CPU. A 200×200 grid is used and the time step is equal to △t=0.0001 s. The computations are carried out for 1000 time steps in theanalysis of pure natural convection (Ri=∞). Note that the immersed boundary computational time for the indirect scheme is about two times greater than the time consumed in the Dirichlet boundary condition implementation. For the direct scheme, the consumed time is three times greater than the Dirichlet case. Also, the post processing computational time for the indirect method is considerably less than the direct method (and also the Dirichlet boundary condition case).
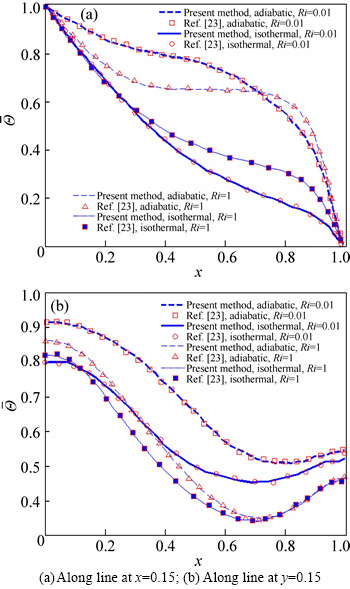
Fig. 12 Effect of Richardson number value on temperature:
5.3 Mixed convection around a hot rotating circular cylinder in a square enclosure
Mixed convection heat transfer around a hot rotating cylinder in a cold square enclosure (ΘC=0) is modeled in the third test case. Dirichlet (ΘH=1) and Neumann ( Θ/
Θ/ n=-1) boundary conditions on the surface of the cylinder are considered in this case. The computational cost is higher in the rotating cylinder case, as compared to the stationary cylinder, due to the fact that normal vectors at IB points are time dependent and should be re-calculated at each time step.
n=-1) boundary conditions on the surface of the cylinder are considered in this case. The computational cost is higher in the rotating cylinder case, as compared to the stationary cylinder, due to the fact that normal vectors at IB points are time dependent and should be re-calculated at each time step.
The radius of cylinder is r=0.2L, L being the length of each side of the square, as shown in Fig. 13. Note that only an angular coordinate is used to address the locations along both inner and outer boundaries.
Computational results are reported for five Richardson numbers, Ri=1, 10, 100, 1000 and ∞ (natural convection) at a fixed Prandtl number (Pr=0.71) and also a fixed Rayleigh number (Ra=106). The non-dimensional temperature is defined by Eq. (5) and Eq. (6) for isothermal and iso heat flux boundary conditions respectively. Length and velocity scales are L0=L and u0=ωr, where ω is the rotational speed of the cylinder. Here again a uniform 200×200 Cartesian grid is used to descretize the space and the time step is equal to △t=0.0001 s. In the case of Ri=∞, which corresponds to the pure natural convection, the velocity scale is u0=α/L.
Table 2 Effect of boundary condition type on computational time in the second test case
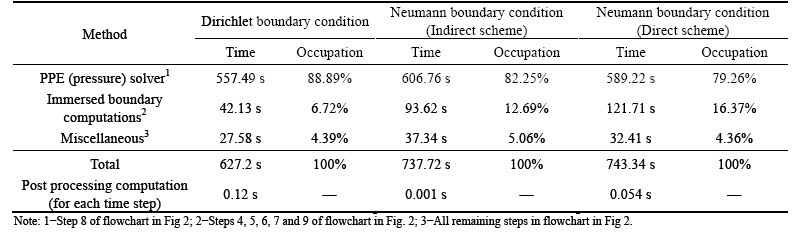
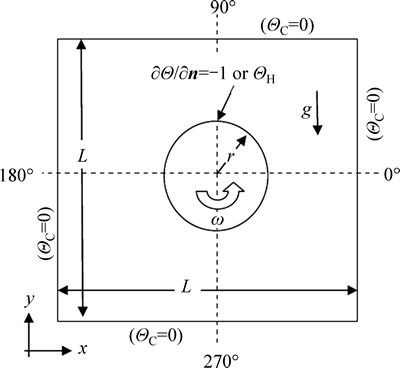
Fig. 13 Computational domain and boundary conditions for third test case
5.3.1 Dirichlet (iso-thermal) boundary condition
Figure 14 shows the isotherms and streamlines at different Richardson numbers. At Ri=1, which corresponds to a high Reynolds number, the flow pattern is clearly rotation-dominated. At higher Richardson numbers, the induced secondary flow pattern due to the effect of natural convection becomes stronger. At Ri=10, the main rotational flow and the induced secondary flow are comparable and at Ri=1000 the induced secondary flow becomes dominant. At pure natural convection, i.e. at Ri=∞, a symmetric induced flow is formed around the cylinder.
Figures 15(a) and (b) show the distributions of the local Nusselt numbers at the boundaries of the cylinder and the enclosure respectively. Good agreement with the results given by LIAO and LIN [24] is observed.
As shown in Fig. 15(a), when the flow is rotation-dominated (corresponding to Ri=1), the local Nusselt number on the surface of the cylinder is rather uniformly distributed. By increasing the Richardson number, a local minimum appears in the distribution of the Nusselt number. By increasing the Richardson number, the location of this minimum value moves towards the position corresponding to θ=90° and the value of this minimum decreases gradually.
As shown in Fig. 15(b), the local Nusselt number changes periodically along the outer surface for Ri=1. By increasing the Richardson number, a dominant local maximum Nusselt number is formed which moves towards the position corresponding to θ=90° gradually at higher Richardson numbers. The maximum value of the Nusselt number increases by increasing the Richardson number gradually.
5.3.2 Neumann (iso-heat flux) boundary condition
Implementation of the iso heat flux at the boundary is considered here to study the performance of the direct and indirect schemes for a moving boundary. Heat transfer around a rotating cylinder with isoheat flux boundary condition has not been studied before in the context of immersed boundary method.
As shown in Fig. 16, variation of the local convection heat transfer coefficient is negligible at low Richardson numbers. However, at higher Richardson numbers the minimum convection heat transfer coefficient occurs at a particular point on the cylinder. At Ri=1000, the induced secondary flow becomes dominant. For the pure natural convection, Ri=∞, a symmetric induced flow is formed around the cylinder.
Figures 17(a) and (b) show the distributions of the local Nusselt numbers at the boundaries of the cylinder and the enclosure respectively. When the flow is rotation-dominated (corresponding to Ri=1), the local Nusselt number on the surface of the cylinder is rather uniformly distributed. By increasing the Richardson number, a local minimum appears in the distribution of the Nusselt number, which moves towards the positioncorresponding to θ=90° at higher Richardson numbers. For the pure natural convection case, the position of the minimum Nusselt number corresponds to θ=90°, which is also the location of maximum temperature.
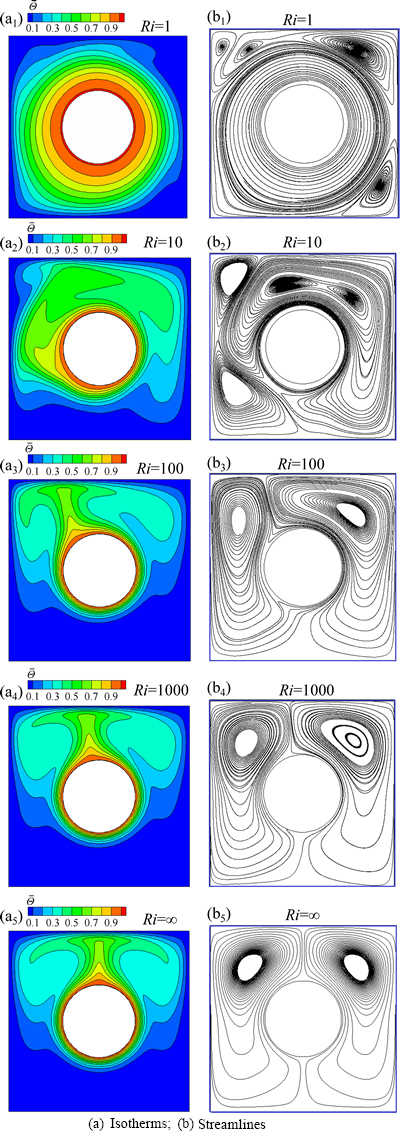
Fig. 14 Isotherms and streamlines at different values of Richardson number for the third test case:
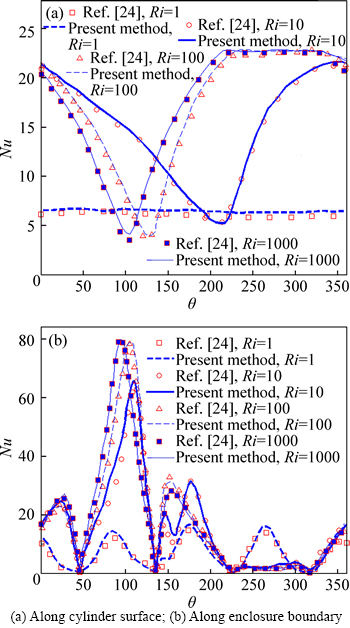
Fig. 15 Local Nusselt numbers at various Richardson numbers:
As shown in Fig. 17(b), the local Nusselt number changes periodically along the outer surface for Ri=1. By increasing the Richardson number, a dominant local maximum Nusselt number is formed which moves towards the position corresponding to θ=90° gradually at higher Richardson numbers. The maximum value of the Nusselt number increases by increasing the Richardson number gradually.
To have a sense regarding the relative computational costs of different calculations, a comparison is provided in Table 3. A 200×200 grid is used here and the time step is equal to △t=0.0001 s. The computations are carried out for 1000 iterations in a mixed convection case (Ri=10). It can be seen that the immersed boundary computational time has increased about 40%, as compared to the stationary cylinder case.
6 Conclusions
1) The iterative direct forcing immersed boundary method is extended and used for the solution of convection heat transfer problems. The body force,pressure and heat source at boundary points are calculated simultaneously in an iterative process to accurately impose all boundary conditions. Direct and indirect methods are proposed and implemented to impose Neumann boundary condition.
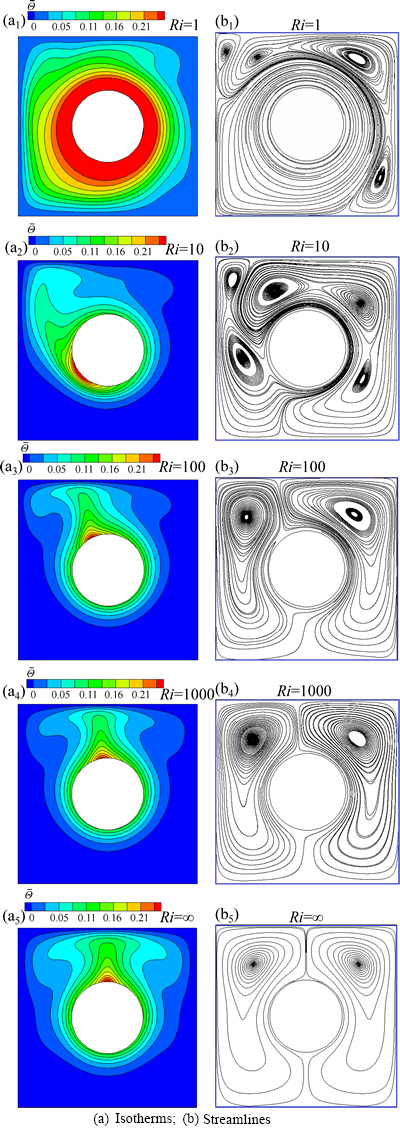
Fig. 16 Isotherms and streamlines at different values of Richardson number for third test case:
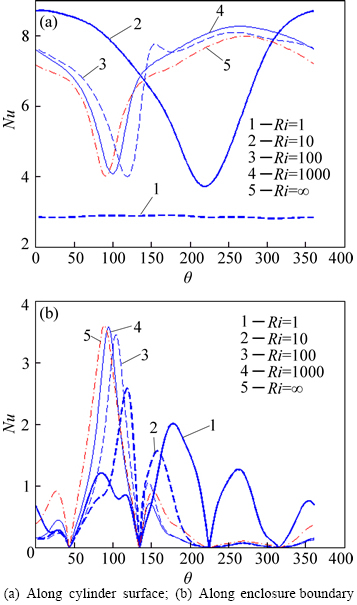
Fig. 17 Local Nusselt numbers at various Richardson numbers in the third test case:
2) Flow patterns as well as temperature fields are presented in a number of carefully selected test cases. Test cases include forced convection on a heated cylinder in an unbounded flow field, mixed and natural convection around a circular body in a lid-driven cavity, and mixed and natural convection around a heated rotating cylinder in a square enclosure. The computed Nusselt numbers along the boundary of the domain in all test cases are in excellent agreement with the available computational results.
3) The direct method has a higher order of accuracy compared to the indirect method of imposition of the Neumann boundary condition. Regarding the computational time for the stationary boundary cases, the implementation of Dirichlet boundary condition is the least expensive and the indirect and direct methods to impose Neumann boundary condition require 2 and 3 times more computational time respectively in immersed boundary computation. Additional computational time is required for the moving boundary cases due to the time dependency of the boundary normal vectors. The post processing time, required to calculate the Nusselt number, is higher for the direct method as compared to the indirect method as well as Dirichlet boundary condition implementation.
Table 3 Effect of boundary condition type on computational time in the third test case
Appendix A: Derivation of Eq. (41)
In this appendix an alternative approach is devised to derived Eq. (41).
Equation (37) can be written for an arbitrary IB point (shown in Fig. 1(b) as follows:
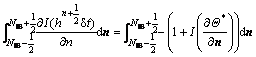 (A1)
(A1)
The heat flux difference, 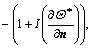 is supposed to be constant at an IB point. Therefore, Eq. (A2) can be rewritten as follows:
is supposed to be constant at an IB point. Therefore, Eq. (A2) can be rewritten as follows:
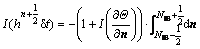 (A2)
(A2)
Considering the magnitude of the normal vector and the fact that there are two normal directions at each IB point, the remaining integral in Eq. (A2) is estimated as 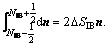 Equation (A2), therefore, can also be written as follows:
Equation (A2), therefore, can also be written as follows:
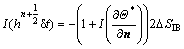 (A3)
(A3)
By applying the distribution operator, defined in Section 3.1, Eq. (41) is obtained.
Appendix B: Discretization on staggered grids
A finite difference method on a staggered grid is used in this work. The immersed boundary is discretized by IB points, shown by  in Fig. B1(a). Four types of points need to be defined in this two-dimensional staggered grid arrangement as shown in Fig. B1(b). These are the u and v grid points, shown respectively by → and ↑, cell centers, shown by hollow circles, and Eu points shown by
in Fig. B1(a). Four types of points need to be defined in this two-dimensional staggered grid arrangement as shown in Fig. B1(b). These are the u and v grid points, shown respectively by → and ↑, cell centers, shown by hollow circles, and Eu points shown by  . The cell centers are used to store scalars such as pressure and temperature.
. The cell centers are used to store scalars such as pressure and temperature.
The velocity components at the u and v grid points are calculated in the prediction step. Velocity components at Eu points are then obtained as follows:
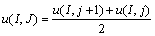 (B1)
(B1)
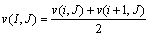 (B2)
(B2)
Also, temperature and pressure are calculated at the Eu points as follows:
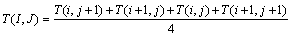 (B3)
(B3)
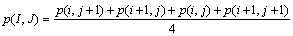 (B4)
(B4)
The variables at Eu points are then used to calculate force and heat sources at IB points as explained in the body of the work. The source terms are transferred to Eu points and used to modify the velocity components and temperature as follows:
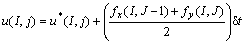 (B5)
(B5)
 (B6)
(B6)
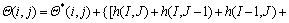
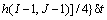 (B7)
(B7)
Equations (B5), (B6) and (B7) are in fact the same as Eqs. (46) and (47) on a staggered grid where fx and fy are the components of the force vector at Eu points.
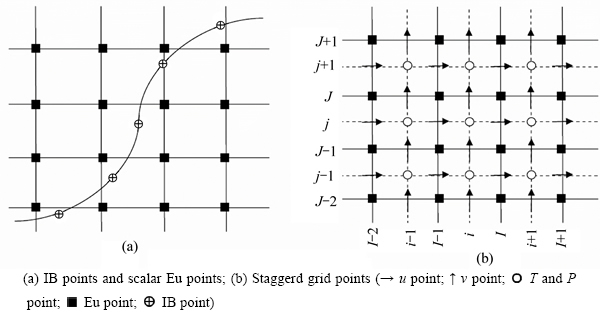
Fig. B1 Staggered grid arrangement:
Nomenclature
cp
Heat capacity
D(Φ)
Distribution operator
fe
External momentum source
fne
Non-dimensional external momentum source
F
Non-dimensional external momentum source on IB point
fx, fy
Non-dimensional external momentum source components
g
Gravitational acceleration
△x
non-dimensional uniform Cartesian grid size
I(f)
Interpolation operator
k
Coefficient of thermal conductivity
L0
Problem-dependent length scales
n
Normal vector on IB point
nx, ny
Normal vector component on IB point
Nu
Nusselt number
p
Pressure
pn
Non-dimensional pressure
Pr
Prandtl number
h
External heat source
QΓ
Specified heat flux
H
Non-dimensional external heat source on IB point
Re
Reynolds number
Ri
Richardson number
Ra
Rayleigh number
t
Time
tn
Non-dimensional time
T
Temperature
Θ
Non-dimensional temperature
TH, TC
Hot and cold reference temperatures
Θ*
Non-dimensional intermediate temperature
ΘΓ
Non-dimensional body surface temperature
Θ
Non-dimensional temperature on IB point
u
Velocity vector
u0
Problem-dependent velocity scales
u*
Intermediate velocity
u
Non-dimensional velocity vector
U
Non-dimensional velocity on IB point
u, v
Non-dimensional velocity components
VΓ
Non-dimensional boundary velocity
x
Eu point coordinate vector
xn
Eu point non-dimensional coordinate vector
XIB
Coordinate vector of IB point
x, y
Eu point non-dimensional coordinate vector components
XIB, YIB
IB point coordinate vector components
α
Thermal diffusivity
β
Coefficient of thermal expansion
△
Discrete delta function
ρ
Density
v
Kinematic viscosity
ω
Rotational speed of the cylinder
Ψ
Stream function
△Ψ
Stream function difference
Ψmin, Ψmax
Minimum and maximum values of stream function
 /
/ x
x
Derivatives with respect to x
 /
/ y
y
Derivatives with respect to y
NIB
IB point number
Superscript
n
Time step
i
inner loop iteration index
k
outer loop iteration index
Subscript
IB
IB point
References
[1] PESKIN C S. Flow patterns around heart valves: A numerical method [J]. Journal of Computational Physics, 1972, 10: 252-271.
[2] GOLDSTEIN D, HADLER R, SIROVICH L. Modeling a no-slip flow boundary with an external force field [J]. Journal of Computational Physics, 1993, 105: 354-366.
[3] SAIKI E M, BIRINGEN S. Numerical simulation of a cylinder in uniform flow: Application of a virtual boundary method [J]. Journal of Computational Physics, 1996, 123: 450-465.
[4] MOHD-YUSOF J. Combined immersed boundaries/B-splines methods for simulations of flows in complex geometries [M]// CTR Annual Research Briefs. Stanford: NASA Ames Research Center, 1997: 317-327.
[5] FADLUN E, VERZICCO R, ORLANDI P, MOHD-YUSOF J. Combined immersed-boundary finite-difference methods for three- dimensional complex flow simulations [J]. Journal of Computational Physics, 2000, 161: 35-60.
[6] BALARAS E. Modeling complex boundaries using an external force field on fixed Cartesian grids in large-eddy simulations [J]. Computers & Fluids, 2004, 33: 375-404.
[7] MITTAL R, DONG H, BOZKURTTAS M, NAJJAR F M, VARGAS A, von LOEBBECKE A. A Versatile sharp interface immersed boundary method for incompressible flows with complex boundaries [J]. Journal of Computational Physics, 2008, 227: 4825-4852.
[8] UHLMANN M. An immersed boundary method with direct forcing for the simulation of particulate flows [J]. Journal of Computational Physics, 2005, 209: 448-476.
[9] WANG Z, FAN J, LUO K. Combined multi-direct forcing and immersed boundary method for simulating flows with moving particles [J]. International Journal of Multiphase Flow, 2008, 34: 283-302.
[10] JI C, MUNJIZA A, WILLIAMS J J R. A novel iterative direct-forcing immersed boundary method and its finite volume applications [J]. Journal of Computational Physics, 2012, 231: 1797-1821.
[11] PAN D. An Immersed boundary method on unstructured Cartesian meshes for incompressible flows with heat transfer [J]. Numerical Heat Transfer B, 2006, 49: 277-297.
[12] YOON H S, LEE J B, CHUN H H. A numerical study on the fluid flow and heat transfer around a circular cylinder near a moving wall [J]. International Journal of Heat and Mass Transfer, 2007, 50: 3507-3520.
[13] WANG Z, FAN J, LUO K, CEN K. Immersed boundary method for the simulation of flows with heat transfer [J]. International Journal of Heat and Mass Transfer, 2009, 52: 4510-4518.
[14] KIM B S, LEE D S, HA M Y, YOON H S. A numerical study of natural convection in a square enclosure with a circular cylinder at different vertical locations [J]. International Journal of Heat and Mass Transfer, 2008, 51: 1888-1906.
[15] MARK A, SVENNING E, EDELVIK F. An immersed boundary method for simulation of flow with heat transfer [J]. International Journal of Heat and Mass Transfer, 2013, 56: 424-435.
[16] PACHECO J R, PACHECO-VEGA A, RODIC T, PECK R E. Numerical simulations of heat transfer and fluid flow problems using an immersed-boundary finite volume method on nonstaggered grids [J]. Numerical Heat Transfer B, 2005, 48: 1-24.
[17] ZHANG N, ZHENG Z C, ECKELS S. Study of heat-transfer on the surface on a circular cylinder in flow using an immersed-boundary method [J]. International Journal of Heat and Fluid Flow, 2008, 29: 1558-1566.
[18] PAN D. A general boundary condition treatment in immersed boundary methods for Incompressible Navier-Stokes Eqs with heat transfer [J]. Numerical Heat Transfer B, 2012, 61: 279-297.
[19] REN W, SHU C, YANG W. An efficient immersed boundary method for thermal flow problems with heat flux boundary conditions [J]. International Journal of Heat and Mass Transfer, 2013, 64: 694-705.
[20] PESKIN C. The immersed boundary method [J]. Acta Numerica, 2002, 11: 479-517.
[21] BHARTI R P, CHHABRA R P, ESWARAN V. A numerical study of the steady forced convection heat transfer from an unconfined circular cylinder [J]. International Journal of Heat and Mass Transfer, 2007, 43: 639-648.
[22] AHMAD R A, QURESHI Z H. Laminar mixed convection from a uniform heat flux horizontal cylinder in a crossflow [J]. J Thermophys Heat Transfer, 1992, 6: 277-287.
[23] KHANAFER K, AITHAL S M. Laminar mixed convection flow and heat transfer characteristics in a lid-driven cavity with a circular cylinder [J]. International Journal of Heat and Mass Transfer, 2013, 66: 200-209.
[24] LIAO C C, LIN C A. Mixed convection of a heated rotating cylinder in a square enclosure [J]. International Journal of Heat and Mass Transfer, 2014, 72: 9-22.
(Edited by FANG Jing-hua)
Cite this article as: Ali Akbar Hosseinjani, Ali Ashrafizadeh. An extended iterative direct-forcing immersed boundary method in thermo-fluid problems with Dirichlet or Neumann boundary conditions [J]. Journal of Central South University, 2017, 24(1): 137-154. DOI: 10.1007/s11771-017-3416-x.
Received date: 2015-11-12; Accepted date: 2016-02-18
Corresponding author: Ali Akbar Hosseinjani, PhD Candidate; Tel: +98-2184063309; E-mail: aahosseinjani@mail.kntu.ac.ir

