DOI: 10.11817/j.issn.1672-7207.2019.06.030
考虑辅助停车区约束的中速磁浮列车速度曲线节能优化方法
柴晓凤1,刘军1, 2,赖晴鹰1,孟令云1,丁文亮1,徐亚之2
(1. 北京交通大学 交通运输学院,北京,100044;
2. 北京交通大学 轨道交通控制与安全国家重点实验室,北京,100044;
3. 中车唐山机车车辆有限公司,河北 唐山,064000)
摘要:在分析中速磁浮列车动力学模型和节能运行工况转换序列的基础上,提出一种先以运行线路参数为依据划分场景,然后在特定场景中以双限速度防护曲线的临界点为依据进一步细分区间的建模思想,进而构建满足目标运行时间约束下的多区间列车速度曲线节能优化模型,并给出一种基于不同运行工况转换点的求解思路以及多区间列车节能速度曲线的Pareto优化方法。研究结果表明:与现有列车速度曲线节能优化方法对比,本文优化方法针对磁浮列车运行的适用性和优化效果更好。
关键词:铁路运输;中速磁浮;速度曲线;辅助停车区;Pareto
中图分类号:U293.1 文献标志码:文献标识码:A 文章编号:1672-7207(2019)06-1499-08
Optimal energy-efficient trajectory planning for middle-speed maglev considering constraint of auxiliary stopping area
CHAI Xiaofeng1, LIU Jun1, 2, LAI Qingying1, MENG Lingyun1, DING Wenliang1, XU Yazhi2
(1. School of Traffic and Transportation, Beijing Jiaotong University, Beijing 100044, China;
2. State Key Laboratory of Rail Traffic Control and Safety, Beijing Jiaotong University, Beijing 100044, China;
3. CRRC Tangshan Co. Ltd., Tangshan 064000, China)
Abstract: Based on the analysis of the kinetic equations of the middle-speed maglev and the switching sequence of energy-efficient operation conditions, the running line was divided into different scenes according to the line parameter. Then the scene was divided into different sections further according to the crossover point of the double protected curve. The model was established to optimize energy-efficient trajectory of multiple sections under the constraint of the target running time. And then the model was given a resolving thought based on different switching point of operation conditions and the Pareto optimization method to optimize the energy-efficient trajectory planning of multiple sections. The results show that the applicability and optimization for the maglev of the optimization method is better than that of the existing energy-efficient trajectory planning optimization methods.
Key words: railway transportation; middle-speed maglev; trajectory planning; auxiliary stopping area; Pareto
《“十三五”国家科技创新规划》[1]中强调要加强中速磁浮的关键技术与设备研发。时速为200 km/h的中速磁浮列车作为一种新型交通方式将在我国大城市群的城际和市郊大容量、高密度通勤交通中有重要地位。通过优化列车运行速度曲线,即满足一定约束条件下,在目标运行时间内完成运输距离且寻找能耗最小化的速度曲线[2-3],对于降低中速磁浮运行能耗具有重要作用。目前,既有轮轨列车运行能耗的研究主要集中于列车速度曲线的节能优化。ICHIKAWA[4]采用最优控制理论对列车速度曲线问题进行了研究。MILROY等[5]建立了最小化牵引能耗的速度曲线优化模型,提出最优速度曲线只运用于“最大牵引、惰行、最大制动”3种有限运行工况;ASNIS等[6]采用Dubovitskii-Milyutin最大值原理证明列车最优速度曲线是由“最大牵引、巡航、惰行、最大制动”4种运行工况组成。之后,HOWLETT等[7-9]在分析列车节能运行工况、工况转换序列以及工况转换点时,提出采用非线性方法求解工况转换点,从而构成求解列车节能速度曲线的基本方法。宿帅[10]结合城轨列车牵引效率特性建立节能速度曲线优化模型,基于能耗提出工况转换点的求解和优化方法,其优化目标是节时、节能,但较少考虑制动能量的消耗,且缺乏乘客舒适度约束。目前,针对磁浮列车运行能耗研究中,因磁浮区间有限,研究成果较少。崔杰[11]采用计算机仿真绘制了中低速磁浮列车在快速、舒适、经济等不同运行策略下的速度曲线,却未考虑辅助停车区的影响。杨柯[12]在线路限速、辅助停车区影响、乘客舒适度约束等条件下,通过设计磁浮仿真平台生成最优速度曲线,但其仿真方法较为耗时。杨光[13-14]采用在最短时间速度曲线的基础上确定惰行切换点的方式优化高速磁浮列车的速度曲线,但线路选择的是单一限速、无坡度的运行区段,不适用于线路限速变化频繁的区段。与轮轨铁路列车相比,磁浮列车加减速能力强、时间短,对乘客舒适度影响较大,且磁浮线路中辅助停车区的设置使列车运行速度需满足双限速度防护约束,故现有轮轨列车速度曲线优化研究难以直接应用于磁浮系统。现有磁浮列车速度曲线优化研究中同时考虑辅助停车区影响和多限速、不同坡度的线路场景约束的研究成果较少。因此,本文作者对基于多工况(最大牵引、巡航、惰行、最大制动)、多约束(运行时间约束、辅助停车区约束、舒适度约束等)、多场景(不同限速、坡度)的中速磁浮列车速度曲线优化问题进行研究。
1 问题描述
中速磁浮列车的动力学模型是计算列车速度曲线的基本依据,也是分析列车节能运行工况、工况的转换序列以及序列之间转换点的基础[10]。
1.1 列车运行动力学方程
磁悬浮列车纵向受力示意图如图1所示。中速磁浮列车运行过程中受到同步直线电机的牵引力 、制动力
、制动力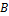 、列车运行阻力
、列车运行阻力 共同作用。由于磁浮列车运行时不与轨道接触,故与钢轨不存在黏着力,其运行阻力主要包括空气阻力
共同作用。由于磁浮列车运行时不与轨道接触,故与钢轨不存在黏着力,其运行阻力主要包括空气阻力 、坡道重力
、坡道重力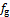 、电磁涡流阻力
、电磁涡流阻力 、直线发电机引起的运行阻力
、直线发电机引起的运行阻力 等[13]。若给定线路条件,则
等[13]。若给定线路条件,则 ,
, 和
和 均可表示为关于速度
均可表示为关于速度 的函数,
的函数,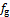 可表示为关于位置
可表示为关于位置 的函数。
的函数。
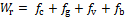 (1)
(1)
列车运行动力学方程如下[13]:
 (2)
(2)
式中: 为列车运行位置;
为列车运行位置; 为时间;
为时间; 为列车运行速度;M为列车质量。
为列车运行速度;M为列车质量。

图1 磁浮列车纵向受力示意图
Fig. 1 Schematic diagram of longitudinal force of maglev train
1.2 节能运行工况及其转换序列
依据中速磁浮列车在运行过程中不同受力情况,一般可将其运行过程分为最大牵引、巡航、惰行、最大制动4种节能运行工况[6],如图2所示。

图2 节能运行工况示意图
Fig. 2 Schematic diagram of energy-efficient operation conditions
列车在相同限速区间内运行时,其节能工况转换序列为最大牵引—巡航—惰行—最大制动,各种工况的持续时间会根据实际情况的不同而有所变化[10]。如图3所示,由于能耗或运行条件等制约,列车无法加速到线路最大限速,其最优转换序列为最大牵引—惰行—最大制动。

图3 最大牵引—惰行—最大制动工况示意图
Fig. 3 Schematic diagram of maximum traction-coasting-maximum braking condition
2 中速磁浮列车速度曲线节能优化模型
由于中速磁浮列车速度曲线优化受到线路参数、辅助停车区设置、运行工况等前提条件的制约,不同约束条件下求解精度差异较大,且既有研究方法均难以解决上述条件制约下的速度曲线优化问题,因此将这些约束条件细分为场景(依据线路参数)、区间(依据辅助停车区设置)、工况等。为精细化求解不同条件下速度曲线优化问题,采用“先划分场景,再细分区间”的两步求解过程建模,进而建立多区间列车速度曲线节能优化模型,在满足运行约束条件下对节能运行工况转换点进行求解和优化。
2.1 运行区间划分
在中速磁浮列车运行过程中,首先要考虑运行线路参数,如坡度、限速等,其中限速包括曲线限速、道岔限速、市区限速等,将坡度以及限速均相同的运行线路定义为同一类场景。此外,还考虑了辅助停车区的影响,由于中速磁浮线路只在车站和辅助停车区铺设动力轨,且提供安全、快捷的疏散通道,以保证旅客安全和方便排除列车故障[15-16],故在任何情况下都必须保证磁浮列车能够安全停在停车区上,即列车运行速度要时刻满足双限速度防护约束[17-18]。在磁浮线路中前后辅助停车区的双限速度防护曲线存在交点,即速度防护区域的临界点,如图4所示。若第 时刻时列车运行速度为
时刻时列车运行速度为 ,而第
,而第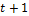 时刻时可选的速度有
时刻时可选的速度有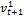 ,
, 和
和 ,可见这3个速度均处于危险速度域外,但当第
,可见这3个速度均处于危险速度域外,但当第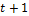 时刻的速度为
时刻的速度为 时,则列车运行速度会跨越危险速度域,不满足双限速度防护约束,故列车行驶至临界点位置时,运行速度应大于临界点速度,保证列车运行安全。
时,则列车运行速度会跨越危险速度域,不满足双限速度防护约束,故列车行驶至临界点位置时,运行速度应大于临界点速度,保证列车运行安全。
中速磁浮列车速度曲线优化问题是一个多约束、多场景的非线性规划问题,求解复杂度大[19],故首先将多场景线路转化为多个单一场景组合考虑,再根据辅助停车区设置情况将单一场景细分为不同区间,进而将线路整体优化问题转化为多区间组合进行优化,且划分场景和区间时,需要考虑线路属性和运行速度安全。因此,本文将中速磁浮列车运行过程依据限速、坡度划分为多个场景,再依据临界点位置细分为多个区间,划分步骤如下:
Step 1 将限速以及坡度相同的线路划分为同一类场景。
Step 2 在同一场景中以临界点为依据再进行区间划分,令临界点位置处于区间边界。
令线路总长度为 ,划分场景数量为
,划分场景数量为 ,
,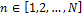 ;划分区间数量为
;划分区间数量为 ,
, ,第k个区间长度为
,第k个区间长度为 ,区间划分示意图如图4所示。
,区间划分示意图如图4所示。

图4 区间划分示意图
Fig. 4 Schematic diagram of section division
2.2 目标函数及约束条件
模型假设如下:
1) 已知线路条件、车辆牵引制动等特性,即已知磁浮线路限速、坡度、辅助停车区等设置,磁浮车辆参数、牵引曲线等;
2) 仅牵引、巡航、制动工况消耗能量,惰行工况能耗视为0,不考虑能量储存和馈能。
本模型优化目标是列车总运行能耗,其约束条件包括线路限速、双限速度防护约束、加速度约束、加速度冲击率约束、边界约束及相邻两区间连接约束等。
目标函数:
 (3)
(3)
式中: 为列车在
为列车在 时刻第
时刻第 区间的牵引力;
区间的牵引力; 为列车在
为列车在 时刻第
时刻第 区间的运行速度;
区间的运行速度; 为列车总运行能耗;
为列车总运行能耗;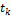 为列车在第
为列车在第 区间的运行时间。
区间的运行时间。
约束条件如下:
1) 线路限速约束:
 (4)
(4)
式中: 为磁浮线路在位置
为磁浮线路在位置 处的限速。
处的限速。
2) 双限速度防护约束:
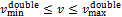 (5)
(5)
式中: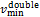 为双限速度防护约束的下限速度;
为双限速度防护约束的下限速度; 为双限速度防护约束的上限速度。
为双限速度防护约束的上限速度。
3) 加速度约束:
 (6)
(6)
式中: 为最大牵引加速度;
为最大牵引加速度; 为最大制动减速度。
为最大制动减速度。
4) 舒适度约束:
 (7)
(7)
式中: =0.50 m/s3,为最大加速度变化率[13]。
=0.50 m/s3,为最大加速度变化率[13]。
5) 边界约束:
 (8)
(8)
式中:Tm为目标总运行时间。
6) 相邻两区间连接约束:
 (9)
(9)
式中: ,
, 和
和 分别为列车到达第
分别为列车到达第 个区间的时间、位置和速度;
个区间的时间、位置和速度; ,
,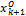 和
和 分别为列车从第
分别为列车从第 个区间出发的时间、位置及速度,第
个区间出发的时间、位置及速度,第 区间到达的运行状态和第
区间到达的运行状态和第 区间出发的运行状态相同。
区间出发的运行状态相同。
2.3 模型求解
本文构建模型时将运行线路“先划分场景,再细分区间”,为了降低求解难度,求解模型时针对各子区间采用分层迭代优化,即第1层求解单个区间节能运行工况转换点,目标是每个区间列车运行时间最小;第2层在给定工况转换点的基础上,采用Pareto寻优方法迭代分配能量优化多个区间节能运行工况转换点,目标是在满足总运行时间约束下使列车运行能耗最低,如图5所示。

图5 分层优化示意图
Fig. 5 Schematic diagram of hierarchy optimization
2.3.1 节能工况转换点的求解
对于限速、坡度均相同的磁浮运行区间 ,列车最短运行时分条件下的最大运行能耗为
,列车最短运行时分条件下的最大运行能耗为 。令列车初速度为
。令列车初速度为 ,
,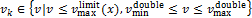 ,令列车初始总能耗为
,令列车初始总能耗为 ,
, 。给定
。给定 和
和 ,计算中速磁浮列车区间节能工况转换点,求解得到的区间列车运行时间最小,且运行能耗不超过初始总能耗。第k个区间节能操纵策略如下:若下一区间限速比该区间限速值高或者与之相同,考虑牵引、巡航和惰行的工况序列转换;若下一区间速度比该区间的低,考虑巡航、惰行和制动的工况序列转换。算法流程如图6所示,其中,
,计算中速磁浮列车区间节能工况转换点,求解得到的区间列车运行时间最小,且运行能耗不超过初始总能耗。第k个区间节能操纵策略如下:若下一区间限速比该区间限速值高或者与之相同,考虑牵引、巡航和惰行的工况序列转换;若下一区间速度比该区间的低,考虑巡航、惰行和制动的工况序列转换。算法流程如图6所示,其中,
 为第
为第 区间的线路限速;
区间的线路限速; =
= 为牵引曲线;
为牵引曲线; =
= 为惰行曲线;
为惰行曲线; 为常用制动加速度;n为初始总能耗分配比例;Eb为制动能耗;△e为制动能耗增加单元。
为常用制动加速度;n为初始总能耗分配比例;Eb为制动能耗;△e为制动能耗增加单元。
2.3.2 Pareto优化节能工况转换点
给定 和
和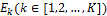 ,可根据磁浮线路参数和列车运行特点,按照节能工况点求解方法得到初始节能速度曲线,该曲线对应的是列车最短时间速度曲线。由于是在最大运行能耗范围内给定的初始总能耗,运行时间可能不满足目标总运行时间约束,需优化节能工况转换点,使运行时间逼近目标总运行时间。因此本文通过Pareto寻优方法优化多个区间的节能速度曲线,使其满足目标运行时间下能耗最低,算法流程如图7所示,其中,△E为分配给区间的能量单元;Ek为分配能量单元后k区间的运行能耗;△Tk为给区间i分配能量单元后缩短的运行时间。
,可根据磁浮线路参数和列车运行特点,按照节能工况点求解方法得到初始节能速度曲线,该曲线对应的是列车最短时间速度曲线。由于是在最大运行能耗范围内给定的初始总能耗,运行时间可能不满足目标总运行时间约束,需优化节能工况转换点,使运行时间逼近目标总运行时间。因此本文通过Pareto寻优方法优化多个区间的节能速度曲线,使其满足目标运行时间下能耗最低,算法流程如图7所示,其中,△E为分配给区间的能量单元;Ek为分配能量单元后k区间的运行能耗;△Tk为给区间i分配能量单元后缩短的运行时间。

图6 第k区间工况转换点求解算法流程图
Fig. 6 Flow diagram of algorithm to solve the kth section switching point of operation conditions

图7 Pareto优化节能速度曲线算法流程图
Fig. 7 Flow diagram of algorithm to optimize energy-efficient trajectory planning by Pareto
3 算例验证
3.1 试验数据
中速磁浮线路试验长度为20.00  ,其中,辅助停车区设置、线路限速、线路坡度等线路参数如表1~3所示,线路示意图如图8所示。试验采用车辆为中车唐山机车研制的中速磁浮列车,车辆参数如下:采用2辆编组,质量
,其中,辅助停车区设置、线路限速、线路坡度等线路参数如表1~3所示,线路示意图如图8所示。试验采用车辆为中车唐山机车研制的中速磁浮列车,车辆参数如下:采用2辆编组,质量 =32
=32  ,最大牵引加速度
,最大牵引加速度 =1.00
=1.00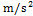 ,常用制动加速度
,常用制动加速度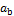 =-1.10
=-1.10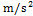 ,紧急制动加速度
,紧急制动加速度 =-1.30
=-1.30  。
。

图8 中速磁浮线路示意图
Fig. 8 Schematic diagram of middle-speed maglev line
表1 辅助停车区设置
Table 1 Auxiliary stopping area km

表2 线路限速
Table 2 Speed limit of line

表3 线路坡度
Table 3 Gradient of line

3.2 结果分析
本文采用Matlab软件进行仿真计算。算例验证中,根据2.1节将运行线路划分为17个区间,即 =17。令仿真步长为
=17。令仿真步长为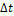 =0.10
=0.10  ,能耗分配比例为
,能耗分配比例为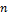 =60%,制动能耗增加单元为
=60%,制动能耗增加单元为 =0.10
=0.10 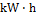 ,分配区间的能量单元为
,分配区间的能量单元为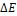 =0.50
=0.50 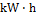 。计算可得每个区间的最大运行能耗为
。计算可得每个区间的最大运行能耗为 =[8.60, 5.70, 6.30, 6.40, 6.70, 9.10, 8.70, 5.00, 4.00, 10.90, 7.70, 3.90, 3.30, 7.90, 3.50, 5.50],令初始总能耗为
=[8.60, 5.70, 6.30, 6.40, 6.70, 9.10, 8.70, 5.00, 4.00, 10.90, 7.70, 3.90, 3.30, 7.90, 3.50, 5.50],令初始总能耗为 =[8.60, 5.60, 6.10, 5.60, 6.70, 8.00, 8.70, 5.00, 3.50, 4.00, 7.70, 3.30, 3.00, 1.60, 3.50, 3.40],目标总运行时间
=[8.60, 5.60, 6.10, 5.60, 6.70, 8.00, 8.70, 5.00, 3.50, 4.00, 7.70, 3.30, 3.00, 1.60, 3.50, 3.40],目标总运行时间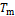 =540.00
=540.00  ,误差允许范围为
,误差允许范围为 0.50
0.50  。
。
3.2.1 优化结果分析
优化后列车运行时间为539.70  ,运行能耗为82.08
,运行能耗为82.08 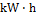 ,目标运行时间误差为-0.30
,目标运行时间误差为-0.30  ,满足目标总运行时间的要求。在优化过程中,列车运行能耗和运行时间的变化情况如图9所示。从图9可见:随着列车运行能耗的增加,运行时间逐渐减小,但运行时间减小的幅度逐渐变缓。
,满足目标总运行时间的要求。在优化过程中,列车运行能耗和运行时间的变化情况如图9所示。从图9可见:随着列车运行能耗的增加,运行时间逐渐减小,但运行时间减小的幅度逐渐变缓。

图9 运行能耗与运行时间关系
Fig. 9 Diagram of operation energy consumption and running time
3.2.2 优化方法对比分析
宿帅[10]采用列车节能速度曲线的优化方法,其运行工况转换点的求解算法是牵引—巡航—惰行—制动,其中忽略了制动能耗。在考虑制动能耗条件下,将本文算法与文献[10]的优化曲线进行对比,结果如图10所示。由图10可见:文献[10]的优化得到的能耗比本文算法的结果低,但其得到的运行速度曲线存在多处(如图10中圈出的位置所示)加速度变化率大于0.50  ,不满足磁浮运行舒适度条件。故本文算法不仅实现磁浮列车速度曲线节能优化,且克服了既有文献难以解决多约束条件下优化的不足。
,不满足磁浮运行舒适度条件。故本文算法不仅实现磁浮列车速度曲线节能优化,且克服了既有文献难以解决多约束条件下优化的不足。

图10 本文算法与文献[10]优化曲线对比
Fig. 10 Comparison of optimization curves of algorithms in this paper and Ref.10
表4 本文算法与文献[13]算法优化结果对比
Table 4 Comparison of optimization results of algorithms in this paper and Ref.[13]

杨光[13]采用最小能量速度曲线的优化方法,即在最短时间速度曲线上确定惰行切换点来降低运行能耗。将本文算法与文献[13]的算法进行比较,结果如图11所示。由图11可见:在最短时间速度曲线上仅有3处位置可选择惰行切换点,虚线即为可选择的惰行曲线,但可能存在跨越限速分区的危险(如图11中阴影区域所示),比较可得:图11中实点所标示位置即为最小能量控制下惰行工况切换的起始点和终止点。令目标总运行时间Tm为562.00 s,优化结果如表4和图12所示。可见;本文优化方法得到的能耗更低,且针对磁浮列车的适用范围更广,避免跨越限速分区的危险。因此,本文算法不仅实现磁浮列车速度曲线节能优化,且克服了既有文献难以解决多场景下优化的不足。
综上可知,文献[10]和[13]中的算法只解决了某个特定约束或场景下速度曲线优化问题,而本文算法除实现既有算法效果外,还考虑了制动能耗、乘客舒适度条件、双限速度防护约束及多限速区段的适用性等,能更好地解决多工况、多约束、多场景下的列车速度曲线优化问题。
4 结论
1) 在中速磁浮动力学模型及节能运行工况转换序列的基础上,提出一种考虑限速约束和辅助停车区设置的列车速度曲线节能优化模型,该模型将坡度、限速等作为划分场景的依据,将双限速度防护临界点作为进一步细分区间的依据。在不同的区间中,考虑运行约束条件下通过分层优化进行求解,先给出每个区间多运行工况转换点的求解方法,再通过Pareto寻优分配能量单元优化多区间列车节能速度曲线。

图11 文献[13]最短时间速度曲线惰行切换点示意图
Fig. 11 Schematic diagram of coasting switching points of shortest time speed curve in Ref.[13]
2) 与既有文献提出的算法相比,本文算法的优化效果更好,对于磁浮线路条件的适用性更强,且能有效克服速度曲线优化问题中多工况、多约束、多场景的不足。
3) 模型中考虑列车再生制动能量将是未来研究的方向之一。

图12 本文算法与文献[13]优化曲线对比
Fig. 12 Comparison of optimization curves of algorithms in this paper and Ref.[13]
参考文献:
[1] 国务院. “十三五”国家科技创新规划[EB/OL]. [2016—08—08]. http://www.gov.cn/zhengce/content/2016-08/08/content_5098072.htm.
State Council. “13th Five-Year” National Science and Technology Innovation Plan[EB/OL]. [2016—08—08].http://www.gov.cn/zhengce/content/2016-08/08/content_5098072.htm.
[2] 李玉生, 侯忠生. 基于遗传算法的列车节能控制研究[J]. 系统仿真学报, 2007, 19(2): 384-387.
LI Yusheng, HOU Zhongsheng. Study on energy-saving control for train based on genetic algorithm[J]. Journal of System Simulation. 2007, 19(2): 384-387.
[3] 荀径, 杨欣, 宁滨, 等. 列车节能操纵优化求解方法综述[J]. 铁道学报, 2014, 36(4): 14-20.
XUN Jing, YANG Xin, NING Bin, et al. Survey on trajectory optimization for train operation[J]. Journal of the China Railway Society, 2014, 36(4): 14-20.
[4] ICHIKAWA K. Application of optimization theory for bounded state variable problems to the operation of train[J]. JSME International Journal, 1968, 11(47): 857-865.
[5] MILROY, IAN P. Aspects of automatic train control[D]. Leicestershire: Loughborough University. Department of Electronic and Electrical Engineering, 1980: 137-138.
[6] ASNIS I A, DMITRUK A V, OSMOLOVSKII N P. Solution of the problem of the energetically optimal control of the motion of a train by the maximum principle[J]. USSR Computational Mathematics & Mathematical Physics, 1985, 25(6): 37-44.
[7] HOWLETT P. An optimal strategy for the control of a train[J]. The Journal of the Australian Mathematical Society Series B: Applied Mathematics, 1990, 31(4): 454-471.
[8] HOWLETT P. Optimal strategies for the control of a train[J]. Automatica, 1996, 32(4): 519-532.
[9] HOWLETT P G, CHENG J. Optimal driving strategies for a train on a track with continuously varying gradient[J]. The Journal of the Australian Mathematical Society Series B: Applied Mathematics, 1997, 38(3): 388-410.
[10] 宿帅. 城轨列车运行图和速度曲线一体化节能方法[D]. 北京: 北京交通大学电子信息工程学院, 2016: 31-54.
SU Shuai. An energy-efficient approach by integrating the train timetable and speed trajectory in urban rail[D]. Beijing: Beijing Jiaotong University. School of Electronic and Information Engineering, 2016: 31-54.
[11] 崔杰. 中低速磁浮列车运行速度曲线的计算[D]. 成都: 西南交通大学电气工程学院, 2012: 37-52.
CUI Jie. Calculation of operating speed curve on medium and low speed maglev train[D]. Chengdu: Southwest Jiaotong University. School of Electrical Engineering, 2012: 37-52.
[12] 杨轲. 磁浮列车仿真平台设计及运控算法研究[D]. 杭州: 浙江大学电气工程学院, 2008: 50-86.
YANG Ke. Research on design and operation control algorithm of maglev train simulation platform[D]. Hangzhou: Zhejiang University. College of Electrical Engineering, 2008: 50-86.
[13] 杨光. 高速磁浮列车最优速度曲线及其跟踪控制研究[D]. 北京: 北京交通大学电子信息工程学院, 2007: 43-83.
YANG Guang. Study on high speed maglev train optimum speed curve and its tracking control[D]. Beijing: Beijing Jiaotong University. School of Electronic and Information Engineering, 2007: 43-83.
[14] YANG Guang. Energy-saving operation control strategy of high-speed Maglev train[C]//2008 Chinese Control and Decision Conference. Piscataway, NJ: IEEE, 2008: 2250-2253.
[15] 卞建光. 磁浮列车运行控制系统相关性质及辅助停车区特性研究[D]. 杭州: 浙江大学电气工程学院, 2006: 43-62.
BIAN Jianguang. Research on the related properties of maglev train operation control system and characteristics of auxiliary parking area[D]. Hangzhou: Zhejiang University. College of Electrical Engineering, 2006: 43-62.
[16] 赖晴鹰, 刘军, 许心越,等. 中高速磁悬浮管—控—电一体化优化框架[C]//第十二届中国智能交通年会大会论文集. 北京,2017: 292-298.
LAI Qingying, LIU Jun, XU Xinyue, et al. Integrated optimization framework of the middle-to-high speed maglev on timetable, coast control, electricity[C]//China Intelligent Transportation Annual Conference. Beijing, 2017: 292-298.
[17] 刘进, 吴汶麒. 高速磁悬浮交通二维速度防护曲线及其算法研究[J]. 中国铁道科学, 2002, 23(4): 106-110.
LIU Jin, WU Wenqi. Research on two-dimensional speed protection curve and algorithm of high speed maglev traffic[J]. China Railway Science, 2002, 23(4): 106-110.
[18] 江亚, 吴汶麒, 刘进. 磁浮列车运行控制系统二维速度防护曲线仿真[J]. 同济大学学报(自然科学版), 2004, 32(3): 397-400.
JIANG Ya, WU Wenqi, LIU Jin. Simulation of high-speed maglev train 2-D speed protection curve[J]. Journal of Tongji University(Science and Technology), 2004, 32(3): 397-400.
[19] DONG Hairong, ZHANG Lingying, CHEN Yao, et al. Multi-objective train trajectory design based on dynamic programming[C]// Proceedings of the 33rd Chinese Control Conference. Piscataway, NJ: IEEE, 2014: 9060-9065.
(编辑 赵俊)
收稿日期: 2018 -07 -20; 修回日期: 2018 -10 -16
基金项目(Foundation item):国家重点研发计划项目(2016YFB1200601);中央高校基本科研业务费专项资金资助项目(2018YJS094);国家自然科学基金资助项目(71871012)(Project(2016YFB1200601) supported by the National Key R&D Program of China; Project(2018YJS094) supported by the Fundamental Research Funds for the Central Universities; Project(71871012) supported by the National Natural Science Foundation of China)
通信作者:刘军,博士,教授,从事轨道交通运营理论与技术研究;E-mail:jliu@bjtu.edu.cn