面向驾驶员个性化需求的动态路径诱导方法
龙琼1,曾革1, 2,张谨帆1,张蕾1
(1. 湖南城市学院 土木工程学院,湖南 益阳,413000;
2. 长沙理工大学 交通运输工程学院,湖南 长沙,410004)
摘要:基于物理规划的思想,研究面向驾驶员个性化需求的动态路径诱导方法。首先,分析个性化动态路径诱导问题,构建路段交通阻抗的个性化评价指标体系;然后,基于物理规划思想,进行个性化动态路径诱导:面向驾驶员对道路的“可行性”需求动态确定交通路网搜索的几何空间;面向驾驶员对道路的“偏好性”需求,对几何空间内的交通路网阻抗进行个性化评价;面向驾驶员对道路的“最优性”需求,基于Dijkstra算法在动态交通路网中进行最优路径搜索;当路网中的交通阻抗发生变化时,及时更新路网信息,重新搜索从车辆当前位置到目的地的最优路径。研究结果表明:该方法既能体现驾驶员的个性化需求;仿真算例验证了该方法的有效性和可行性。
关键词:交通工程;动态路径诱导;物理规划;个性化需求;驾驶偏好;Dijkstra算法
中图分类号:U491.4 文献标志码:A 文章编号:1672-7207(2013)05-2124-06
Dynamic route guidance method facing driver’s individual demand
LONG Qiong1, ZENG Ge1, 2, ZHANG Jinfan1, ZHANG Lei1
(1. School of Civil Engineering, Hunan City University, Yiyang 413000, China;
2. School of Traffical and Transportation Engineering, Changsha University of Science & Technology, Changsha 410004, China)
Abstract: A dynamic route guidance method facing the driver’s individual demand was advanced based on physical programming theory. Firstly, the personalized dynamic route guidance problem was analyzed and the individualized evaluation index system of road traffic impedance was constructed. Then, based on physical programming theory, the method of individual dynamic route guidance was studied as follows: Aiming at the driver’s feasibility demand on the road, the dynamic traffic road network geometry space for searching was determined. Aiming at the driver’s preference demand on the road, the evaluation of the traffic network impedance in the geometry space was individualized. Aiming at the driver’s optimality demand on the road, the optimal path was searched on Dijkstra algorithm in dynamic transportation network. When the traffic network impedance changed, the new optimal path from the current position of the vehicle to the destination would be re-searched by updating network information. The results show that the method can fully reflect the driver’s personal demands. Simulation examples validate the feasibility and effectiveness of the method.
Key words: traffic engineering; dynamic route guidance; physical programming; individual demand; driving preference; Dijkstra algorithm
动态路径诱导研究的核心问题是:在动态的交通路网中,找出1条考虑驾驶员路径选择行为的最优道路,从而使得驾驶员顺利地从起点到达终点[1-4]。在传统的路径诱导方法研究中,一般以出行时间最短或出行距离最短作为优化目标。这种方法虽然降低了最优路径搜索问题的难度,但是,由于忽略了驾驶员的个性化需求,诱导系统向不同驾驶员提供的最优路径是一样的,这将引起出行者的过度反应或集聚效应,从而导致拥挤漂移现象。拥挤漂移现象的产生会使得路网中的交通流处于失衡状态,同时,这会大大增加驾驶员对交通诱导系统的不信任度,从而对交通流诱导技术的应用与推广产生较大的负面影响。鉴于此,一些学者提出采用k-最短路算法来同时求取多条候选路径供驾驶员选择,将最后的决策权留给驾驶员[5-8]。此种方法能有效分散交通流,缓解拥挤漂移问题,但同时带来了需要驾驶员对各条路径的进行个性化评价的问题。孙燕等[9-12]利用灰色理论、模糊数学、神经网络等方法探讨了该问题。但在通常情况下,这些路径搜索与路径评价相互独立:路径搜索基于传统的静态交通路网即可完成;而在路径评价过程中需要能够反映驾驶员个性化需求的交通信息,两者对交通路网的信息需求的不一致性,给实际应用带来了一定的难度。驾驶员对于路径选择的行为特征较复杂,不同驾驶员选择最优路径的标准不是固定不变的。为此,本文作者在分析个性化动态路径诱导问题的基础上,提出一种面向驾驶员个性化需求的动态路径诱导方法。首先,构建路段交通阻抗评价指标体系,基于物理规划的思想,动态确定相应的路网搜索空间;其次,引入驾驶员偏好因子,对搜索空间各路段进行实时综合评价,得到反映驾驶员个性化需求的各路段综合交通阻抗;而后利用Dijkstra算法实现最优路径搜索, 由此获得的最优路径既考虑了各出行影响因素, 又充分体现了不同驾驶员的出行意愿。
1 个性化动态路径诱导问题
将交通路网表达为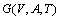 。其中:V为路网所有节点vi的集合;A为所有路段Ai,j的集合;下标i和j为路网节点标识;
。其中:V为路网所有节点vi的集合;A为所有路段Ai,j的集合;下标i和j为路网节点标识;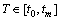 为路阻变化可获知或预测的时间段。设路段Ai,j的阻抗为
为路阻变化可获知或预测的时间段。设路段Ai,j的阻抗为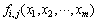 ,表示从节点vi出发到节点vj的交通阻抗函数;
,表示从节点vi出发到节点vj的交通阻抗函数;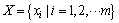 ,为交通阻抗评价指标,则个性化动态路径诱导问题可以描述为:基于能够全面反映路网特征的评价指标体系X,引入驾驶员的个性化偏好因子,构建能够反映驾驶员个性化特征的交通路网
,为交通阻抗评价指标,则个性化动态路径诱导问题可以描述为:基于能够全面反映路网特征的评价指标体系X,引入驾驶员的个性化偏好因子,构建能够反映驾驶员个性化特征的交通路网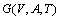 ,并从中寻找1条从t0时刻出发、自起始点v0到目标点vN的最能够满足驾驶员个性化需求的路径
,并从中寻找1条从t0时刻出发、自起始点v0到目标点vN的最能够满足驾驶员个性化需求的路径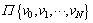 ,并使得目标函数最小。因此,构建合适的评价指标体系,将驾驶员的个性化偏好实时地表达在交通路网
,并使得目标函数最小。因此,构建合适的评价指标体系,将驾驶员的个性化偏好实时地表达在交通路网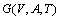 中是本文研究的重点。
中是本文研究的重点。
2 评价指标体系构建
评价某条路段的优劣时,仅仅考虑其行程距离或者行程时间是不够的,还应该考虑可行路段的特点、驾驶员的个性需求、特定出行的性质(如目的、预算)以及驾驶环境(如天气、白天晚上)等因素,因此,路段评价具有一定的主观性,因人而异。从驾驶员的角度考虑,理想最优路径的确定过程应综合考虑各主要出行影响因素并充分体现驾驶员的主动性[13]。本文综合考虑驾驶员的个性化需求,构建路段综合交通阻抗评价指标体系如下:
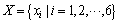 (1)
(1)
其中:x1为路段行程距离;x2为路段每公里行程时间;x3为舒适度,综合考虑路段的拥挤程度、车道数、道路质量等级、行人及非机动车数量等因素的影响而获得的路段评价指标;x4为安全度,根据路段交通事故率来度量;x5为路段每公里行程费用,主要考虑路段收费和油耗;x6为路段沿途景观,户外游玩时,沿途景观往往是1个需要考虑的因素。值得说明的是,x2为路段每公里行程时间,实际等价于对路段行驶速度的评价。
这些指标从总体上可分为定性指标和定量指标。定性化指标无量纲包括舒适度和沿途景观,本文采用定性等级评分法来描述各指标;定量化指标可以通过测算、建模等方法来获得,如行程距离、行程时间、安全度和行程费用,但各指标之间的量纲不同。具体地说,建立评价指标的度量标准如表1所示。
表1 评价指标度量标准
Table 1 Metrics of evaluation

从表1可以看出:对于每条道路,其每公里行程时间、舒适度、安全度、行程费用和沿途景观等指标的行驶代价均与路段行程距离直接相关,即当路段越长时,因行程时间、舒适度、安全度、行程费用、沿途景观产生的路阻代价将越大。
3 基于物理规划的个性化动态路径诱导
3.1 物理规划的基本思路
物理规划是一种处理多目标优化设计问题的有效方法。该方法能够从本质上把握使用者的偏好,是处理多目标优化问题的新框架。其基本思路是[14-15]:引入偏好函数,描述评价主体对某一评价指标的个性化需求;引入偏好因子,将不同物理意义的各种评价指标转换为具有相同数量级的无量纲的满意度目标;通过优化,寻求对综合目标的满意度最优解作为问题解。在一般情况下,设计评价指标的偏好函数仅为Class1-S型(设计指标越小越好)和Class2-S型(设计指标越大越好),以Class1-S型为例(见图1),对某一设计指标进行区间划分,其中xi1~xi5是设计者根据其偏好给定的评价指标xi的区间端点值。
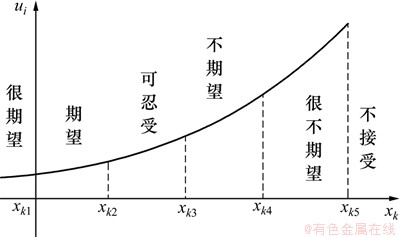
图1 驾驶员对道路评价指标的偏好函数
Fig.1 Preference function of drivers on road evaluation index
从图1可以看出:加驾驶员对路径的个性化选择过程可以描述为:在各项路径评价指标均可接受的范围内,通过在动态交通路网中合理表达自身的个性化需要,自动搜索获得最符合个性化需求的行车路径。因此,综合考虑路径诱导的特点,驾驶员的个性化需求可分为以下3个层次。
第1层次为“可行性”需求,即路径诱导结果必须满足驾驶员的基本要求,如道路驾驶舒适度指标必须大于或等于某值。
第2层次为“偏好性”需求,即驾驶员对各指标的偏好程度,如一般情况下,与行程时间指标相比,驾驶新手更注重道路的安全性指标。
第3层次为“最优性”需求,即路径诱导在满足驾驶员“可行性”需求的基础上,根据其“偏好性”需求,尽可能使各评价指标达到综合最佳值。
因此,基于物理规划思想的个性化动态路径诱导的基本思路是:首先,面向驾驶员对道路的“可行性”需求,根据车辆当前位置和目的地位置,动态确定交通路网搜索的几何空间;其次,面向驾驶员对道路的“偏好性”需求,引入驾驶员选路过程中的偏好因子,对几何空间内的交通路网阻抗进行个性化评价,得到路段交通综合阻抗;最后,面向驾驶员对道路的“最优性”需求,基于Dijkstra算法在动态确定的交通路网中搜索最优路径,实时输出当前路网阻抗状态下的最优路径。当路网中的交通阻抗发生变化或驾驶员行驶途中变更个性需求时,及时更新路网信息,按照前述基本思路,重新搜索从车辆当前位置到目的地的最优路径。
3.2 面向驾驶员“可行性”需求的交通路网空间动态确定
为了提高算法执行效率,在大规模路网下需要对算法的搜索区域进行有效限制。考虑到驾驶员对道路指标的“可行性”需求,通过如下方式确定搜索交通路网几何空间。
Step 1 “可行性指标”设定。在规划之前,按照交互方式,确定驾驶员对道路的评价指标的可行性指标值xk5 (见图1,k=1, 2, …, 6)。值得注意的是:对于行程距离指标,驾驶员关心的是行驶总路程,所以,将x15设置为某个大于1的常数,当驾驶员的行驶总路程为车辆当前位置与目标点位置距离的x15倍时,则认为是不可行的;其他指标x25~x65则按照单条道路进行可行性指标进行设定。
Step 2 交通路网几何空间限定。假设车辆当前位置到目标点的直线距离为lod,令a=x15lod/2,以车辆当前位置与目标点位置为椭圆焦点,以a为椭圆长轴作椭圆,则椭圆限定的区域为交通路网搜索的可行几何空间。
Step 3 可行几何空间的个性化裁剪。根据x25~x65,对椭圆限定区域的搜索空间进行裁剪,以满足驾驶员对行驶途中的每公里行驶时间、舒适度、安全度、综合费用和沿途景观的“可行性”需求。
由此,动态确定了能够满足驾驶员“可行性”需求的交通路网空间。
3.3 面向驾驶员“偏好性”需求的路网交通阻抗综合评价
从交通路网评价指标体系可以看出:各路段的行程时间、舒适度、安全度、行程费用和沿途景观等行驶代价均与路段行程距离直接相关,从路阻代价的角度考虑,当路段行程距离越长时,因行程时间、舒适度、安全度、行程费用、沿途景观产生的路阻代价将越大。据此,设计路阻函数如下:
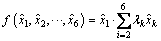 (2)
(2)
其中: 为路段行程距离的测量值;
为路段行程距离的测量值;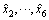 分别为不同物理意义的各种评价指标
分别为不同物理意义的各种评价指标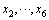 转换为[0,1]区间的无量纲满意度评价指标,本文统一将其转换为Class1-S型(设计指标越小越好),即
转换为[0,1]区间的无量纲满意度评价指标,本文统一将其转换为Class1-S型(设计指标越小越好),即
 (3)
(3)
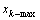 和
和 分别为对应指标xk的最大值和最小值;
分别为对应指标xk的最大值和最小值;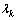 为驾驶员在选路过程中对于不同指标的偏好 因子。
为驾驶员在选路过程中对于不同指标的偏好 因子。
从式(2)可知:当不同路段的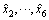 均设置为定值时,式(1)转化为最短路径模型;当
均设置为定值时,式(1)转化为最短路径模型;当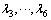 均设置为0时,式(1)转化为最少时间模型。
均设置为0时,式(1)转化为最少时间模型。
偏好因子 的引入体现了驾驶员的对路径诱导的偏好性需求,简化了驾驶员判断指标相对重要性的复杂程度,解决了优化排序过程中的一致性问题。评价指标框架如图2所示。
的引入体现了驾驶员的对路径诱导的偏好性需求,简化了驾驶员判断指标相对重要性的复杂程度,解决了优化排序过程中的一致性问题。评价指标框架如图2所示。
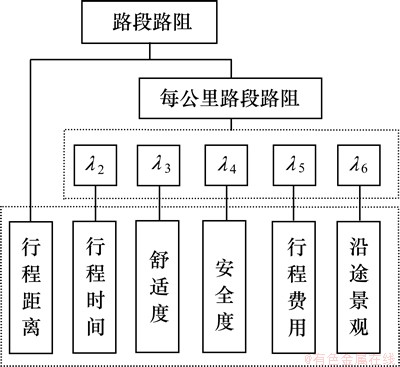
图2 层次化交通阻抗综合评价体系
Fig.2 Comprehensive evaluation system of hierarchical traffic impedance
为了体现驾驶员的个性化偏好,按照偏好程度逐渐下降的顺序,将其分为6个等级:“极重要”、“很重要”、“重要”、“稍重要”、“不重要”、“不关心”, 并按照主观赋权法设置相应的值,分别为:9,7,5,3,1和0,通过归一法确定相应的偏好系数 。
。
3.4 面向驾驶员“最优性”需求的动态最优路径搜索
基于Dijkstra算法[9]动态求解最优路径。由于在路网动态确定和交通阻抗综合评价的过程中已经充分考虑了驾驶员的“可行性需求”和“偏好性”需求,因此,诱导路径是符合驾驶员的个性特点的,而考虑到路网交通阻抗的特点,在此进行最优路径搜索时采用如下目标函数:
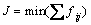 (4)
(4)
其中:fij表示路Ai,j的阻抗。当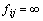 时,节点vi和vj不连通。
时,节点vi和vj不连通。
首先,根据路网交通拓扑图构建联接矩阵F:
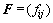 (5)
(5)
然后,利用Dijkstra算法,从起始车辆当前位置出发,逐步搜索到目标点,并记录相应的代价,最终得到代价最优的可行路径。
在车辆行驶过程中,当路网中的交通阻抗变化超过一定阈值或驾驶员个性需求变更时,及时更新路网信息,按照前述基本思路,重新搜索从车辆当前位置到目的地的最优路径。
4 仿真算例
为了验证本文方法的有效性,以长沙城区路径诱导为背景进行仿真验证,交通网络如图3所示。
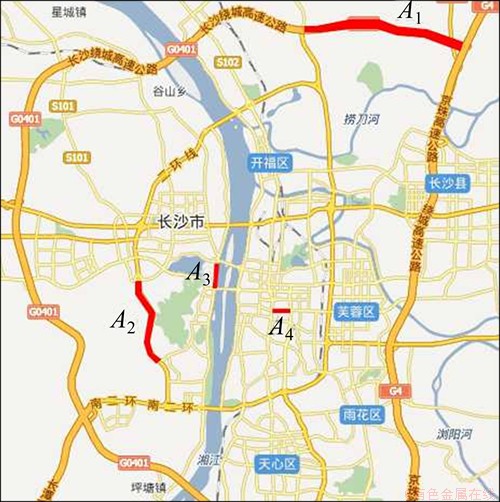
图3 长沙城区交通网络
Fig.3 Traffic network of Changsha
作为路径诱导的基础,路段交通阻抗属性表的建立非常重要,基于路段评价指标体系,本文构建对路段描述的数据结构为
道路={长度,时间,合适度,安全性,费用,风景}
其中:时间、舒适度、安全性、费用、风景均存储各路段具有相同数量级的无量纲满意度评价指标值,以图3中所示路段A1~A4为例,其路段阻抗如表2所示。表2中:A1为绕城高速路段,时间代价很小而费用代价最高(高速收费);A2为环线路段,路况较好,时间代价较小,但存在车辆多、超速现象严重等问题,导致安全代价较大;A3为沿江大道,车道宽敞,行车流畅,舒适度代价最低,沿江风光带风景宜人,与橘子洲遥遥相望,沿途景观代价近似为0;A4为繁华商业街区,车多拥挤,行驶缓慢,施工颇多,各种指标代价都很大。
表2 路段交通阻抗示例
Table 2 Sample of road traffic impedance
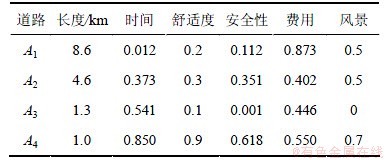
假设一驾驶员从S点出发,到达目标T点,按照传统的路径诱导算法,搜索得到最优路径如图4所示(其中:line1为最少时间路径,line2为最短距离路径。)
显然,上述路径仅仅针对是单一指标的优化结果,当驾驶员需要对行程中的安全性、舒适性等其他指标有要求时,该结果显然难以满足其个性化需求。下面通过2个算例来验证本文方法的有效性。
图4 传统诱导方法搜索结果
Fig.4 Search results of traditional induction method
4.1 算例1
为了体现驾驶员的个性化需求,通过人机交互的方式,确定驾驶员的“可行性”需求,确定相应的搜索空间;假设该驾驶员对行程中的风景和安全性能非常关心,偏好设置为:行程时间“不重要”,舒适度“重要”,安全度“极重要”,行程费用“稍重要”,沿途景观“极重要”。根据主观赋值法进行赋值,并进行归一化,可得行程时间、舒适度、安全性、费用、风景相应的偏好系数λ2~λ6: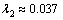 ,
,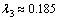 ,
,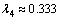 ,
,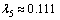 ,
,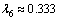 。从而得到相应的搜索路径如图5所示。
。从而得到相应的搜索路径如图5所示。
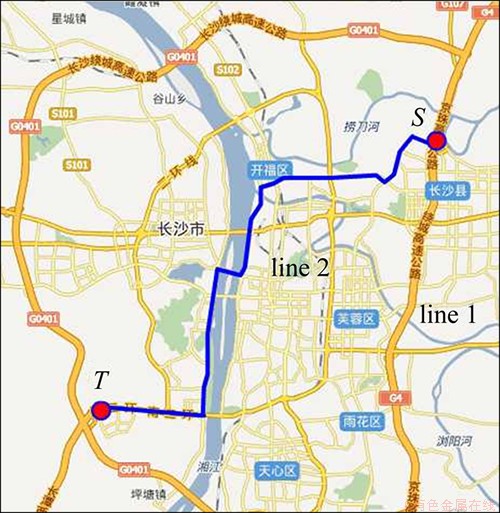
图5 情况1的个性化路径诱导结果
Fig.5 Results of personalized route guidance for Case 1
从图5可以看出:所选路径避开了城市中心,道路宽敞、车流量较少,行车通畅,保证了驾驶员的安全性需求;同时,该路径大部分经历沿江风光带,能够饱览橘子洲和岳麓山畔的自然风光,符合驾驶员的沿途景观需求。
4.2 算例2
假设另一驾驶员从同一起点出发,到达同一目的点,其个性化偏好为:行程时间“很重要”,舒适度“稍重要”,安全度“稍重要”,行程费用“极重要”,沿途景观“不关心”。依据本文诱导方法得到结果如图6所示。
从图6可以看出:所选路径以环线行驶为主,路径较短、车道宽敞、红绿灯较少、车行通畅,能够保证行程时间“很重要”的个性化需求;同时,该路径避开了沿环城高速行驶带来的行程费用代价,符合驾驶员的期望需求。
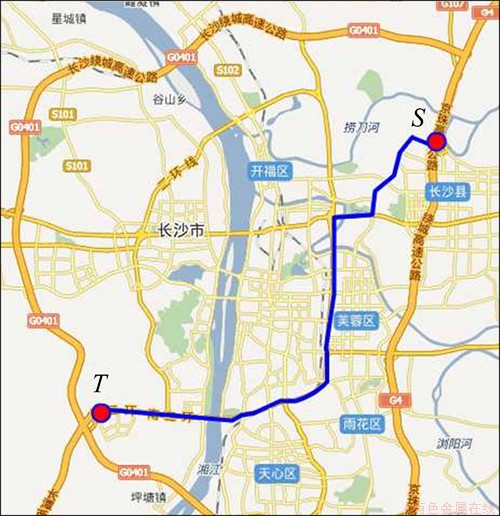
图6 情况2的个性化路径诱导结果
Fig.6 Results of personalized route guidance for Case 2
5 结论
(1) 基于物理规划的思想,提出了一种个性化动态路径诱导方法。该方法充分考虑驾驶员对路径诱导的个性需求,体现驾驶员选择路径的主动性。
(2) 通过驾驶员个性化需求在路径诱导过程中的实时表达,在一定程度上避免了分布式动态导航系统中的拥挤漂移现象,提高了整个交通系统运行效率。
(3) 以长沙城区路径诱导为背景进行仿真,并与传统的最少时间/最短路径诱导算法结果进行对比,验证了本文方法的有效性和可行性,获得的最优路径既考虑了各种因素对出行的影响, 又充分体现了不同驾驶员的出行意愿。
参考文献:
[1] 杨群, 关伟, 张国伍. 基于合理多路径的路径选择方法的研究[J]. 管理工程学报, 2002, 16(4): 42-45.
YANG Qun, GUAN Wei, ZHANG Guowu. Study on multi-path based route choice approach[J]. Journal of Management Sciences in China, 2002, 16(4): 42-45.
[2] Lee C K. A multiple path routing strategy for vehicle route guidance systems[J]. Transportation Research, 1994, 2(3): 185-195.
[3] YANG Qun, ZHAO Yanan. A fuzzy logic-based frame work for route choice in vehicle navigation systems[J]. Journal of Systems Science and Systems Engineering, 2000, 9(4): 467-474.
[4] 杨兆升, 初连禹. 动态路径诱导系统的研究进展[J]. 公路交通科技, 2000, 17(1): 34-38.
YANG Zhaosheng, CHU Lianyu. Study on the development of the dynamic route guidance systems (DRGS)[J]. Journal of Highway and Transportation Research and Development, 2000, 17(1): 34-38.
[5] 于德新, 杨兆升, 高鹏. 动态限制搜索区域的带约束K则最优路径算法[J]. 吉林大学学报: 工学版, 2009, 39(增2): 172-176.
YU Dexin, YANG Zhaosheng, GAO Peng. Constrained K-shortest paths algorithm within dynamic restricted searching area[J]. Journal of Jilin University: Engineering and Technology Edition, 2009, 39(S2): 172-176.
[6] Yen J Y. Finding the K shortest loopless paths in a network[J]. Management Science, 1971, 17(11): 716-721.
[7] Lawler E. Combinatorial optimization: Networks and matroids[M]. New York: Courier Dover Publications, 1976: 92-104.
[8] 王媛, 杨兆升, 高鹏. 预防拥挤漂移的带约束K则最优路径算法[J]. 北京工业大学学报, 2009, 35(3): 345-349.
WANG Yuan, YANG Zhaosheng, GAO Peng. Constrained K-shortest paths algorithm to prevent the congestion shifting problem[J]. Journal of Beijing University of Technology, 2009, 35(3): 345-349.
[9] 孙燕, 陈森发, 黄鹍. 基于灰色评价理论的自适应最优路径选择[J]. 中国公路学报, 2003, 16(4): 87-90.
SUN Yan, CHEN Senfa, HUANG Kun. Adaptive optimal route selection based on gray evaluation theory[J]. China Journal of Highway and Transport, 2003, 16(4): 87-90.
[10] 孙燕, 陈森发, 亓霞, 等. 基于灰色系统理论的最优路径选择方法[J]. 土木工程学报, 2003, 36(1): 94-98.
SUN Yan, CHEN Senfa, QI Xia, et al. Optimal route selection method based on gray system theory[J]. China Civil Engineering Journal, 2003, 36(1): 94-98.
[11] Pang K H, Cran T. Adaptive route selection for dynamic route guidance system based on fuzzy neural approaches[J]. IEEE Transactions on Vehicular Technology, 1999, 48(6): 2028-2041.
[12] 杨兆升, 姜桂艳, 温慧敏. 流体神经网络在交通网用户最优路径选择中的应用研究[J]. 中国公路学报, 1999, 12(增刊): 76-87.
YANG Zhaosheng, JIANG Guiyan, WEN Huimin. Application of fluid neuron network on route choice based on user optimum in traffic network[J]. China Journal of Highway and Transport, 1999, 12(Suppl): 76-87.
[13] 马永锋, 陆键, 项乔君, 等. 基于出行决策的公路网多目标最优路径算法[J]. 交通运输工程学报, 2007, 7(3): 100-105.
MA Yongfeng, LU Jian, XIANG Qiaojun. Optimal route arithmetic with multigoals in highway network based on travel decision-making[J]. Journal of Traffic and Transportation Engineering, 2007, 7(3): 100-105.
[14] McAllister C D, Smpson T W, Kemper L, et al. Robust multiobjective optimization through collaborative optimization and linear physical programming[C]//10th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference. Albany, New York, 2004: 1-16.
[15] Achill M, CHEN Xuan. Visualizing the optimization process in real-time using physical programming[J]. Engineering Optimization, 2000, 32(6): 721-747.
(编辑 陈灿华)
收稿日期:2012-07-12;修回日期:2012-09-23
基金项目:湖南省科技厅资助项目(2012GK3069);湖南省自然科学基金资助项目(07jj6093)
通信作者:龙琼(1967-),女,湖南长沙人,长沙理工大学访问学者,硕士,高级工程师,从事交通管理与控制研究与教学工作;电话:0737-4628998;E-mail: longqiong@126.com