公路桥梁车辆荷载随机过程模型
余志武1，朱红兵1,2，蒋丽忠1，黄星浩1，唐斌1
(1. 中南大学 土木工程学院，湖南 长沙，410075；
2. 武汉科技大学 城市建设学院，湖北 武汉，430070)
摘要：以多年交通量统计数据为基础，利用灰色系统建立交通量增长的灰色GM(1,1)预测模型，进一步利用马尔科夫链对模型进行处理，得到公路交通量增长随机过程预测模型；利用贵新公路(贵州贵阳—新寨)2 a内连续的车辆总质量，将车质量分布函数与交通量预测模型相结合，得到车辆荷载随机过程模型。研究结果表明：该随机过程预测模型精度较高，车辆总质量符合双指数分布规律；由车辆荷载随机过程模型可计算出一定年限内通过桥梁的某车辆荷载总质量范围内的车辆数，从而较好地解决了桥梁疲劳分析和验算时桥梁运营期内荷载疲劳累积计算问题。
关键词：桥梁；疲劳；车辆荷载；灰色系统；马尔科夫链
中图分类号：U441+4 文献标志码：A 文章编号：1672-7207(2011)10-3131-05
Vehicles load stochastic process model of highway bridges
YU Zhi-wu1, ZHU Hong-bing1, 2, JIANG Li-zhong1, HUANG Xing-hao1, TANG Bin1
(1. School of Civil Engineering, Central South University, Changsha 410075, China;
2. Civil Engineering College, Wuhan University of Science and Technology, Wuhan 430070, China)
Abstract: Based on the traffic statistical data of many years, a traffic increasing prediction model was established by using grey system theory, then it is treated with Markov chain, and highway’s traffic increasing stochastic process prediction model was achieved. Utilizing 2 years continual vehicles masses measured at Guixin highway (Guiyang—Xinzai), combined with vehicle’s mass distribution function and traffic prediction model, vehicles load stochastic process model of highway bridges was obtained. The results show that the model has a high precision and vehicle’s mass corresponds with two exponential distributions. The model can figure out vehicle numbers which across the bridge in a certain load mass scope during a certain period, so the model can resolve loads cumulate fatigue calculation problem during fatigue analysis or fatigue checking.
Key words: bridges; fatigue; vehicle load; grey system; Markov chain
疲劳破坏是工程结构和构件失效的主要原因之一，研究疲劳问题具有很重大的现实意义[1]。我国目前服役的桥梁非常多，必须对很多桥梁服役状况进行疲劳评估，或对其剩余服役寿命进行预测，以便于加强对服役桥梁的管理和维护[2]。对于公路桥梁，在对其进行疲劳设计或评估前，必须预先确定或估计在评估期内的荷载历程[3-4]。而荷载历程可以分解为交通量增长历程和组成总交通量的汽车质量变化规律。交通部“公路桥梁车辆荷载研究”课题组通过研究得到了我国公路桥梁标准车辆荷载并将其作为现行设计规范的主要依据[5]。文献[6-10]通过交通量调查，得出了城市道路的疲劳荷载谱或疲劳车模型。这些研究成果有利于桥梁疲劳研究，但上述研究对交通量的调查时间过短，车质量仅根据经验估算，或考虑的仅是荷载及其效应的最大值，并不能很好地用于疲劳分析。如何较准确又比较方便地确定桥梁运营期内的荷载历程，成为疲劳分析的一个较突出问题。在此，本文作者结合灰色系统和马尔科夫链理论，利用多年连续观测的交通量建立基于灰色-马尔科夫随机过程的公路交通量预测模型。通过连续2 a的收费站车辆所称质量，统计出车辆总质量分布规律，最终得到公路桥梁荷载随机过程模型。
1 交通量增长预测方法
影响交通量增长的因素非常繁杂，其规律具有一定的随机性。目前，用于交通量预测的方法虽能预测交通量的发展趋势，但不能反映交通量增长的动态性和随机性。灰色系统预测是基于少量数据的灰因白果律、差异信息原理、平射原理的建模方法，能在数据有限的条件下模仿微分方程，建立具有部分微分方程性质的模型。马尔可夫随机过程是数学中具有马尔可夫性质的无后效性离散时间随机过程，即在已知当前状态的情况下，过程的未来状态与其过去状态无关。由于灰色GM(1,1)模型能预测交通量增长规律，且马尔科夫随机过程能预测交通量增长的随机性规律，为此，将二者结合建立灰色-马尔科夫随机过程公路交通量预测模型。
1.1 灰色GM(1,1)预测模型建模方法
x(0)=(x(0)(1)，x(0)(2)，…，x(0)(n))为GM(1,1)建模序列，x(1)=(x(1)(1)，x(1)(2)，…，x(1)(n))为x(0)的AGO序列。其中：x(1)(1)=x(0)(1)，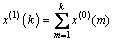
。
z(1)=(z(1)(2)，z(1)(3)，…，z(1)(n))，为x(1)的均值序列，z(1)(k)=0.5x(1)(k)+0.5x(1)(k-1)，则GM(1,1) 模型表达形式为[11]：
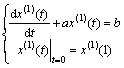
式中：a和b为待定系数。
使用最小二乘法可以求出a和b，代入原式可求出模型对原数据的拟合值。
1.2 灰色GM(1,1)预测模型建模步骤
建立灰色GM(1,1)预测模型主要有以下步骤[12]：(1) 对数据序列进行级比检验及建模可行性判断； (2) 对于级比检验不合格的数据序列进行变换处理，使变换后序列的级比符合建模要求；(3) 先将数据进行累加生成，再利用生成后的数据进行GM(1,1)建模；(4) 根据后验差检验方法对模型进行检验，将预测精度分为“好”、“合格”、“勉强”、“不合格”4类；(5) 通过GM(1,1)模型获取指定时区的预测值。
1.3 马尔科夫随机过程预测方法
设有随机过程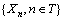
，若对于任意的整数
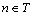和任意的
，条件概率满足：P{Xn+1=in+1|X0=i0，X1=i1，…，Xn=in}=P{Xn+1=in+1+Xn=in}，则称随机序列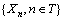为马尔可夫链。马尔可夫链的统计特性完全由条件概率P{Xn+1=in+1+Xn=in}所决 定[13]。
条件概率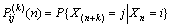
，(i，j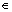
I；n≥0；k≥1)为马尔可夫链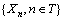的k步转移概率，并称
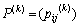为马尔可夫链的k步转移概率。其
中，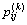
≥0，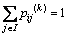
。
1.4 基于灰色马尔科夫随机过程的公路交通量预测方法
灰色马尔科夫随机过程的预测方法就是充分利用灰色理论和马尔科夫随机过程各自优点并弥补其不足的一种新的预测方法。应用该方法进行预测的基本思路是：先建立灰色GM(1,1)模型，求出其预测曲线γ′(k)；再以平滑的预测曲线γ′(k)为基准，划分若干动态的状态区间；根据落入各状态的点计算出马尔可夫转移概率矩阵预测未来状态，从而得出预测值区间；取区间中点，最终得到精度较高的预测值。其具体步骤如下。
(1) 建立GM(1,1)模型。根据灰色系统理论, 得出GM(1,1)模型的γ′(k)=x′(0)(k+1)曲线。
(2) 状态划分。先确定模型的具体考核指标，将时间序列的各数据划入相应的状态区间内。一般以γ′(k)曲线为基准，根据每个预测对象的具体情况，划分成与γ′(k)曲线平行的若干条形区域,每个条形区域构成一个状态区间，任一状态区间Qi表达为Qi=[Q1i，Q2i]。其中：i=1，2，…，n；Q1i=γ′(k)+Ai；Q2i=γ′(k)+Bi。
(3) 计算转移概率。转移概率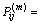
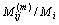。其中：i=1，2，…，n；j=1，2，…，n；
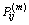为状态Qi经过m步转移到Qi的概率；n为划分的状态数目；Mi为原始数据按一定概率落入状态Qi的样本数；
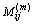为由状态Qi经m步转移到Qj的原始数据样 本数。
(4) 确定未来状态。一般只需通过一步转移来确定交通量的未来状态。
(5) 确定预测值。确定未来预测状态Qd后，也就确定了预测值的变动区间(Q1d，Q2d)，预测值γ′(k)通常取该区间的中点，则有γ′(k)= γ′(k)+(Ai+Bi)/2。
(6) 精度检验。公式为ε(k)=q(0)(k)/x(0)(k)；q(0)(k)=x(0)(k)-x′(0)(k+1)。
1.5 贵新路交通量增长预测
通过交通量的调查，得知贵州省贵新公路(贵阳—新寨)某交通观测站历年交通量如表1所示。以2001年交通量作为初始年交通量，以2001—2006年交通量作为数据序列建模进行交通量增长预测，将2007年数据用于模型校核，建立了GM(1,1)新信息预测模型。交通量预测公式为：
x(0)(k+1)=1 630 217.694 5e0.059 6k
利用该公式所得交通量预测结果及精度见表2。
表1 贵州省贵新公路某交通观测站历年交通量
Table 1 Traffic volume of a traffic observation station at Gui-Xin highway
表2 交通量新信息GM(1,1)模型预测结果
Table 2 Traffic forecast result by new information GM(1,1) model
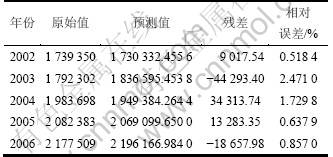
利用交通量新信息GM(1,1)模型，并结合马尔科夫随机过程进行随机桥梁荷载模型研究。将各年份交通量实际值和预测值曲线绘在同一表格，对其状态进行划分。将状态划分为2个，其状态一和状态二的边界线方程为：
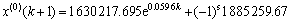
其中：s代表状态，对状态一，s=1；对状态二，s=2。
由状态图得到一步转移概率矩阵为：
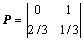
如需预测第N年的交通量，首先需用P(N-2001)求得第N年交通量最有可能处于哪一种状态，再给状态参量s赋值，用下式进一步求得第N年的预测交通量Q(N)，公式为：
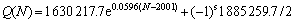
2 公路运营车重分布规律
2.1 分轴型的车辆总质量分布状况
根据贵新路茅草冲大桥附近计质量收费的2007—2008年所有通行车辆相关数据，总结出该路上运营的车辆质量分布规律。
建立车质量分布模型的关键是对客车和货车总质量的随机变量概率函数进行统计分析。其中，客车车质量随机变量分布地域性影响较小，所以，采用文献[5]中的分析结果。
目前，用于描述车质量随机变量的经典数学模型主要有正态分布、对数正态分布、伽马分布、极值I型分布、韦布尔分布及正态加权的多峰分布[14-16]。以收费站2007—2008的货车轴质量统计结果为依据，对上述经典分布参数进行拟合，然后进行K-S检验、A2检验，得到货车2轴车、3轴车、4轴车、5轴车的总质频数直方图及分布拟合曲线，如图1~4所示。
由以上统计直方图和拟合曲线可知：2~4轴货车的随机变量分布函数为不符合经典随机变量的多峰分布函数。5轴货车分布相对有规律，其概率密度函数为：
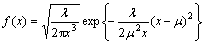
式中：μ＝31 672.3；λ＝249 191。
图1 2轴货车总质量频数直方图及拟合曲线
Fig.1 Frequency histogram and fitting curve of two-axle truck’s total mass
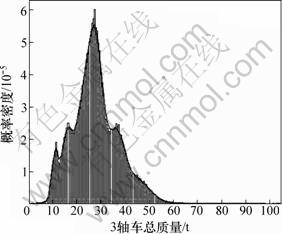
图2 3轴货车总重频数直方图及拟合曲线
Fig.2 Frequency histogram and fitting curve of three-axle truck’s total weight
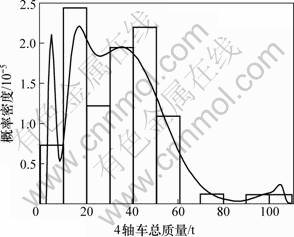
图3 4轴货车总质量频数直方图及拟合曲线
Fig.3 Frequency histogram and fitting curve of four-axle truck’s total mass
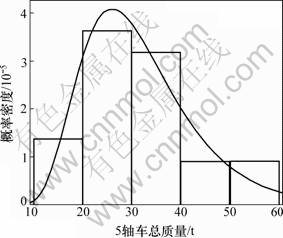
图4 5轴货车总质频数直方图及拟合曲线
Fig.4 Frequency histogram and fitting curve of five-axle truck’s total mass
2.2 车辆总质概率密度函数
由于分轴型的车辆总质量分布规律性不强，考虑到对于桥梁疲劳而言主要是总质量影响较大，而车型影响较小，所以，将所有车辆统一考虑并进行分布拟合。对车辆总质量进行双指数拟合，得到概率密度函数为：
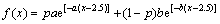
其中：x取值范围为1~77 t；a，b和p为集拟合系数。在95%的保证率下，各系数分别为a=0.072 8，b= 0.666 4，p=0.865 3，拟合平方差之和为0.002 922，平均误差为0.006 46。统计的车质量原始数据及拟合曲线见图5。由图5可见，拟合曲线与原始数据之间吻合程度较高，可以用来描述车辆总质量的分布状况。
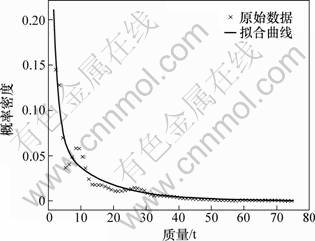
图5 统计的总车质量原始数据及拟合曲线
Fig.5 Original data and fitting curve of truck’s total mass
3 车辆荷载随机过程模型
交通量预测模型为：
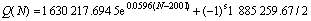
车辆总质量双指数概率密度函数为：
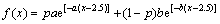
其中：a=0.072 8；b=0.666 4；p=0.865 3。
可以得到第N年的车辆荷载随机过程模型为：
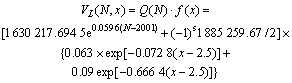
式中：N为待预测交通量的年份；x为车辆总质量(t)。
利用该模型，即可计算出第N年内通过桥梁的某一车辆荷载总质量范围内的车辆数。
4 结论
(1) 对贵州省贵新公路进行调研，获取了该路交通观测站的大量交通量信息及车辆计质量。将灰色GM(1,1)模型与马尔科夫随机过程结合，建立了预测交通量增长的随机过程模型，检验结果表明该模型精度很高。
(2) 将观测到的贵新公路2 a内所有运行车辆计质量进行经典分布拟合，发现其符合双指数分布规律，得到了车辆总质量双指数概率密度函数。
(3) 将交通量增长预测模型与车质量分布的双指数分布函数相结合，得到了桥梁荷载随机过程模型。采用该模型可计算出一定年限内通过桥梁的某一车辆荷载总质量范围内的车辆数，从而较好地解决了桥梁疲劳分析和验算时桥梁运营期内的荷载疲劳累积计算问题。同时，该模型能在预测交通荷载时既掌握其发展趋势，又能发现每年的随机变异，使预测精度更高。
参考文献：
[1] 宋玉普. 混凝土结构的疲劳性能及设计原理[M]. 北京: 机械工业出版社, 2006: 8-10.
SONG Yu-pu. Fatigue behavior and design principle of concrete structures[M]. Beijing: China Machine Press, 2006: 8-10.
[2] Miao T J, Chan T H T. Bridge live load models from WIM data[J]. Engineering Structures, 2002, 24(9): 1071-1084.
[3] Chotickai P, Bowman M D. Truck models for improved fatigue life predictions of steel bridges[J]. Journal of Bridge Engineering, ASCE, 2006, 11(1): 71-80.
[4] Cohen H, Fu G K, Dekelbab W, et al. Predicting truck load spectra under weight limit changes and its application to steel bridge fatigue assessment[J]. Journal of Bridge Engineering, ASCE, 2003, 8(5): 313-320.
[5] “公路桥梁车辆荷载研究”课题组. 公路桥梁车辆荷载研究[J].公路, 1997, 22(3): 8-12.
Research Group of Vehicle Load on Highway Bridge. Research of vehicle load on highway bridge[J]. Highway, 1997, 22(3): 8-12.
[6] 童乐为, 沈祖炎, 陈忠延. 城市道路桥梁的疲劳荷载谱[J]. 土木工程学报, 1997, 30(5): 20-27.
TONG Le-wei, SHEN Zu-yan, CHEN Zhong-yan. Fatigue load spectrum of urban road bridges[J]. China Civil Engineering Journal, 1997, 30(5): 20-27.
[7] 王荣辉, 池春, 陈庆中, 等. 广州市高架桥疲劳荷载车辆模型研究[J]. 华南理工大学学报: 自然科学版, 2004, 32(12): 94-96.
WANG Rong-hui, CHI Chun, CHEN Qin-zhong, et al. Study on the model of the fatigue-loaded vehicles in guangzhou trestle bridges[J]. Journal of South China University of Technology: Natural Science Edition, 2004, 32(12): 94-96.
[8] 童乐为, 沈祖炎. 正交异性钢桥面板疲劳验算[J]. 土木工程学报, 2000, 33(3): 16-21.
TONG Le-wei, SHEN Zhu-yan. Fatigue assessment of orthotropic steel bridge decks[J]. China Civil Engineering Journal, 2000, 33(3): 16-21.
[9] 梅刚, 秦权, 林道锦. 公路桥梁车辆荷载的双峰分布概率模型[J]. 清华大学学报: 自然科学版, 2003, 43(10): 1394-1396.
MEI Gang, QIN Quan, LIN Dao-jin. Bi-modal probabilistic model of highway and bridge vehicle loads[J]. Journal of Tsinghua University: Science and technology, 2003, 43(10): 1394-1396.
[10] Zhu Hong-bing, Yu Zhi-wu. Fatigue load vehicles model of city bridges[C]//Roy sterritt. Second International Conference on Intelligent Computation Technology and Automation. Los Alamitos, California: IEEE Computer Society, 2009: 41-44.
[11] 邓聚龙. 灰色系统理论教程[M]. 武汉: 华中理工出版社, 1990: 11-20.
DENG Ju-long. Grey system theory[M]. Wuhan: Huazhong University of Science and Technology Press, 1990: 11-20.
[12] 刘思峰, 党耀国, 方志耕. 灰色系统理论及其应用[M]. 北京: 科学出版社, 2004: 57-61.
LIU Si-feng, DANG Yao-guo, FANG Zhi-gen. Grey system theory and it’s application[M]. Beijing: Science Press, 2004: 57-61..
[13] Ross S M. 应用随机过程概率模型导论[M]. 北京: 人民邮电出版社, 2007: 181-185.
Ross S M. Introduction to probability models[M]. Beijing: Posts & Telecom press, 2007: 181-185..
[14] Getachew A. Traffic load effects on bridges[D]. Stockholm: Stockholn University, 2003: 21-27.
[15] Nowak A S, Nassif H, De Frain L. Effect of truck loads on bridges[J]. Journal of Transportation Engineering, ASCE, 1993, 119(6): 853-866.
[16] 王钧利, 马春燕. 公路桥梁受车辆动力作用的疲劳可靠性分析[J]. 重庆交通学院学报, 1998, 17(3): 31-37.
WANG Jun-li, MA Chun-yan. Dynamic fatigue reliability of highway bridge under vehicles action[J]. Journal of Chongqing Institute, 1998, 17(3): 31-37.
(编辑 陈灿华)
收稿日期：2010-10-11；修回日期：2010-12-29
基金项目：国家自然科学基金资助项目(50878216)；国家西部交通建设科技项目(200631800019)
通信作者：余志武(1955-)，男，湖南临湘人，教授，博士生导师，从事混凝土结构研究；电话：0731-82655366；E-mail：zhwyu@csu.edu.cn
