Fuzzy-GA based algorithm for optimal placement and sizing of distribution static compensator (DSTATCOM) for loss reduction of distribution network considering reconfiguration
来源期刊:中南大学学报(英文版)2017年第2期
论文作者:Mohammad Mohammadi Mahyar Abasi A. Mohammadi Rozbahani
文章页码:245 - 258
Key words:distribution FACTS (DFACTS); distribution static compensator (DSTATCOM); network reconfiguration; genetic algorithm; fuzzy membership function; power loss reduction
Abstract: This work presents a fuzzy based methodology for distribution system feeder reconfiguration considering DSTATCOM with an objective of minimizing real power loss and operating cost. Installation costs of DSTATCOM devices and the cost of system operation, namely, energy loss cost due to both reconfiguration and DSTATCOM placement, are combined to form the objective function to be minimized. The distribution system tie switches, DSTATCOM location and size have been optimally determined to obtain an appropriate operational condition. In the proposed approach, the fuzzy membership function of loss sensitivity is used for the selection of weak nodes in the power system for the placement of DSTATCOM and the optimal parameter settings of the DFACTS device along with optimal selection of tie switches in reconfiguration process are governed by genetic algorithm (GA). Simulation results on IEEE 33-bus and IEEE 69-bus test systems concluded that the combinatorial method using DSTATCOM and reconfiguration is preferable to reduce power losses to 34.44% for 33-bus system and to 45.43% for 69-bus system.
Cite this article as: Mohammad Mohammadi, Mahyar Abasi, A. Mohammadi Rozbahani. Fuzzy-GA based algorithm for optimal placement and sizing of distribution static compensator (DSTATCOM) for loss reduction of distribution network considering reconfiguration [J]. Journal of Central South University, 2017, 24(2): 245-258. DOI: 10.1007/ s11171-017-3425-4.
J. Cent. South Univ. (2017) 24: 245-258
DOI: 10.1007/s11171-017-3425-4
Mohammad Mohammadi, Mahyar Abasi, A. Mohammadi Rozbahani
Department of Electrical Engineering, Borujerd Branch, Islamic Azad University, Borujerd, Iran
 Central South University Press and Springer-Verlag Berlin Heidelberg 2017
Central South University Press and Springer-Verlag Berlin Heidelberg 2017
Abstract: This work presents a fuzzy based methodology for distribution system feeder reconfiguration considering DSTATCOM with an objective of minimizing real power loss and operating cost. Installation costs of DSTATCOM devices and the cost of system operation, namely, energy loss cost due to both reconfiguration and DSTATCOM placement, are combined to form the objective function to be minimized. The distribution system tie switches, DSTATCOM location and size have been optimally determined to obtain an appropriate operational condition. In the proposed approach, the fuzzy membership function of loss sensitivity is used for the selection of weak nodes in the power system for the placement of DSTATCOM and the optimal parameter settings of the DFACTS device along with optimal selection of tie switches in reconfiguration process are governed by genetic algorithm (GA). Simulation results on IEEE 33-bus and IEEE 69-bus test systems concluded that the combinatorial method using DSTATCOM and reconfiguration is preferable to reduce power losses to 34.44% for 33-bus system and to 45.43% for 69-bus system.
Key words: distribution FACTS (DFACTS); distribution static compensator (DSTATCOM); network reconfiguration; genetic algorithm; fuzzy membership function; power loss reduction
1 Introduction
Distribution systems have been operated radically to facilitate their protection scheme and reduce the short circuit current. Therefore, each load point is fed by a route through the system components to the substation. So these systems have low reliability and high power loss [1]. Optimal operation of a distribution system may be achieved through a combination of methods. Reconfiguration is an important method among them [2]. There are two types of switches in distribution networks, namely, sectionalizing switches that are used to isolate the faulty network and tie switches are utilized to restore power to customers through another route in order to reduce interruption duration in abnormal operation conditions. By status change of switches, the power flow to loads will be changed and consequently affect the power loss, voltages, harmonic distortion level, as well as the system reliability, hence in normal operation condition the distribution network performance can be improved and the cost can be reduced by selecting the correct status of switches [3]. Numerous works have been reported in the literatures proposing methods for optimal reconfiguration of radial distribution systems. In Ref. [4], a reconfiguration method was proposed using a simulated annealing (SA) technique. In Ref. [5], different branch exchange techniques have been proposed for network reconfiguration. In Ref. [6], an automatic selection method of optima reconfiguration has been proposed to minimize losses. In recent years, meta-heuristic based methods have been applied for power system optimization particularly while dealing with combinatory optimization problem, such as optimal reconfiguration [7-11]. In Ref. [12], a reconfiguration method was reported using NSGA. In Ref. [13], a fuzzy multi-objective approach was considered for the power loss reduction, node voltage deviation constraint, branch current loading constraint, and feeder load balancing. In Refs. [14, 15], a network reconfiguration methodology was presented to maximize reliability of the power at the load points and minimize the system power loss. They considered models of various components to evaluate probabilistic reliability. In Refs. [16, 17], a Pareto- optimal micro-genetic algorithm was employed to do a trade-off between the reliability indices and the power loss to find the optimal configuration. Although the network reconfiguration is an effective method to improve the system efficiency without any financial investment, but reconfiguring network may not be able to satisfy the aimed loss reduction and power quality constraints. Therefore, the network reconfiguration is employed with capacitor placement or distributed generators (DG) to achieve better performance. In Ref. [18], a reconfiguration methodology was proposed based on an ant colony algorithm (ACA) that aims at achieving the minimum power loss and increment load balance factor of radial distribution networks with distributed generators. The power system reconfiguration in a radial distribution network for reducing losses and to improve voltage profile has been presented using modified plant growth simulation algorithm with distributed generation [19]. In Ref. [20], presents a new method HAS was presented and different scenarios of DG placement and reconfiguration of network were considered. The work presented in Ref. [21] purposes a methodology for distribution system feeder reconfiguration considering different models of DGs based on availability of wind turbines, solar photovoltaic panels and fuel cell with an objective of minimizing real power loss. In Ref. [22], the authors applied particle swarm optimization for distribution feeder reconfiguration considering DGs. ESMAEILIAN and FADAEINEDJAD [23] proposed distribution system efficiency improvement using network reconfiguration and capacitor allocation. In Ref. [24], the reconfiguration and capacitor placement were employed simultaneously to reduce the power loss. They showed that taking into account these two subjects simultaneously is more effective than considering them separately. A sensitivity index-based methodology was presented in Ref. [25] to minimize the energy loss using network reconfiguration combined with capacitor allocation. The objective of Ref. [26] is to study the optimal feeder reconfiguration problem, the optimal capacitor placement problem, and the problem of a combination of the two. On the other hand, it is not possible to ignore the role of custom power device (CPD) in the improvement of quality, reliability, and availability of distribution system. Therefore, the mitigation option, location, and sizing of the required CPDs should be determined based on the economic feasibility according to the required quality, reliability, and availability of system, which is a major concern in the selection process and needs to be optimized [27]. Nowadays in advance, custom power devices, such as static transfer switches (STS), Distribution-STATCOM or DSTATCOM, unified power quality conditioner (UPQC) and dynamic voltage restorers (DVRs), are some emerging solutions to mitigate the damaging consequences of voltage variations [28].Few reports can be found in the literature regarding the placement issues of CPDs along with reconfiguration to improve power quality and reliability in distribution systems. One of shunt custom power devices which are generally used to solve power quality problems in distribution systems is DSTATCOM. JAZEBI et al [29] applied differential evolution algorithm (DEA) to solve the combinatorial nonlinear optimization problem based on reconfiguration and DSTATCOM allocation in distribution system to mitigate losses and improve voltage profile. Simultaneous reconfiguration, optimal placement of DSTATCOM, and photovoltaic array in a distribution system based on fuzzy-ACO approach for the sake of loss reduction, voltage profile improvement, and increase in the feeder load balancing was analyzed in Ref. [30]. Of course there are some studies that have investigated the optimal placement and sizing of DSTATCOM without considering the reconfiguration process. For instance, authors have analyzed the optimal placement and sizing of DSTATCOM by immune algorithm [31], by using hybrid genetic and ant colony algorithm (ACO) [32], using firefly algorithm [33], using the binary gravitational search algorithm [34]. Also authors have investigated the optimal placement and sizing of DSTATCOM with DG as simulations using PSO algorithm [35] and simultaneously with multiple DG by loss sensitivity based BFO algorithm [36].
This work presents a fuzzy based methodology for distribution system feeder reconfiguration considering DSTATCOM with an objective of minimizing real power loss and operating cost. Installation costs of DSTATCOM devices and the cost of system operation, namely, energy loss cost due to both reconfiguration and DSTATCOM placement, are combined to form the objective function to be minimized. The distribution system tie switches, DSTATCOM location and size have been optimally determined to obtain an appropriate operational condition. In the proposed approach, fuzzy membership function of loss sensitivity is used for the selection of weak nodes in the power system for the placement of DSTATCOM and the optimal parameter settings of this DFACTS device along with optimal selection of tie switches in reconfiguration process are governed by genetic algorithm (GA)
2 DSTATCOM structure
DSTATCOM is a shunt device that injects or absorbs both active and reactive current at a point of common coupling connection. DSTATCOM is also a DC/AC converter consisting of a DC-link capacitor or a DC energy storage device that provides constant DC-link voltage, and a three-phase PWM voltage source converter (VSC) bridge. All these are usually connected to the network via a coupling transformer [37]. A DSTATCOM can work as a synchronous voltage source with a variable magnitude and phase angle. Hence, it is capable of controlling its bus voltage and correcting the power factor. Figure 1 shows a bus in a distribution system equipped with a proposed DSTATCOM. Switch changing can absorb or generate the current by considering control strategy and depend on voltage of common coupling bus. In steady-state operation with heavy loading or some short-circuit events, DSTATCOM typically injects appropriate compensating current to the point of coupling connection, and thus voltage at the load bus regulated by the DSTATCOM will be lifted close to the nominal or a given value [38, 39]. Generally, DSTATCOM has the ability of exchanging active and reactive power simultaneously. The amount of active power exchanging depends on the capacity of energy source.
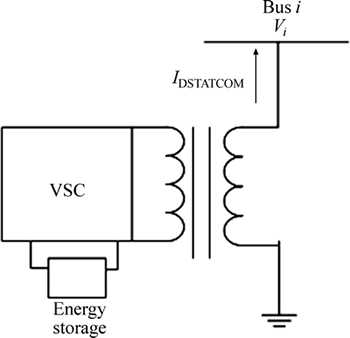
Fig.1 A typical DSTATCOM connected to bus i
Backward/forward sweep load flow calculations are used in this work, in conjunction with a suitable steady state model for DSTATCOM as presented in Ref. [40]. Many distribution networks have radial structures which only feed from one side. A section of a sample distribution network is shown in Fig. 2 [41, 42] which assumes that three-phase radial distribution network is in balance.
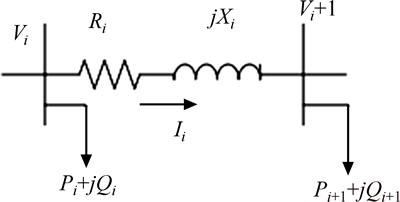
Fig. 2 Single-line diagram of two consecutive buses of a distribution system
Impedance between buses i and i +1 is shown with Ri+jXi. Local loads connected in buses i and i+1 are named Pi+jQi and Pi+1+jQi+1, respectively. Vi and Vi+1 are voltages of these buses. The phasor diagram for Fig. 2 is presented in Fig. 3. KVL equation can be stated as
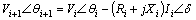 (1)
(1)
Values of variables are derived from load flow. Usually in traditional networks, the buses voltage is less than 1 pu, in the case of which, one can assume that voltage of bus i+1 is also less than 1 pu. A DSTATCOM device is installed in this work in order to compensate voltage of bus i+1 to a desired value. As noted earlier, DSTATCOM is used for voltage regulation and loss reduction in steady state condition and can inject only reactive power to the system. Consequently, IDSTATCOM must be kept in quadrature with respect to the system voltage. As shown in Figs. 4 and 5, by installing DSTATCOM in bus i+1, currents Ii and IDSTATCOM flow in branch simultaneously.
 (2)
(2)
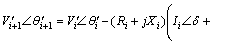
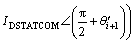 (3)
(3)
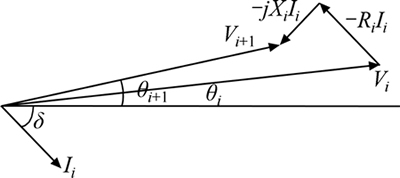
Fig. 3 Phasor diagram of voltage and current of system shown in Fig. 2
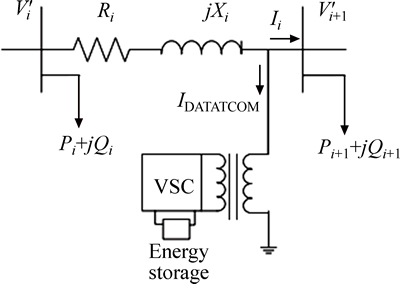
Fig. 4 DSTATCOM installation in bus i+1 of proposed distribution system
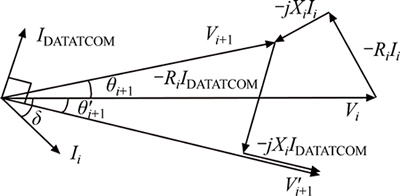
Fig. 5 Phasor diagram of voltage and current of system shown in Fig. 4
By separating the real and imaginary parts of Eq. (3) and some computation, we have
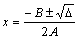 (4)
(4)
That,
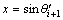
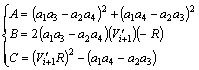 (5)
(5)
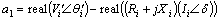 (6)
(6)
 (7)
(7)
 (8)
(8)
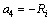 (9)
(9)
As seen from Eq. (4), there are two roots for the variable x, and therefore two values are calculated for  IDSTATCOM and |IDSTATCOM|.
IDSTATCOM and |IDSTATCOM|.
In order to determine the correct answer, the boundary conditions are examined in these roots.
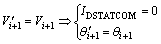 (10)
(10)
Results show that  is the correct answer of Eq. (4). Therefore,
is the correct answer of Eq. (4). Therefore,  can be determined as
can be determined as
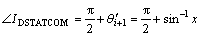 (11)
(11)
Current magnitude of DSTATCOM can be calculated by the appropriate separated real and imaginary equations as
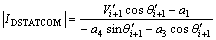 (12)
(12)
Thus IDSTATCOM and voltage of common coupling bus are calculated using Eqs. (10), (11), and (12).
Finally, reactive power injected to the network by DSTATCOM for voltage correction of connected bus up to 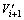 can be expressed as
can be expressed as
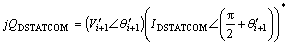 (13)
(13)
3 DSTATCOM modeling in distribution load flow
An accurate load flow model of DSTATCOM should compute the steady state losses, such as transformer and inverter losses. Because of the principle similarities between STATCOM and DSTATCOM structures, the power flow model of STATCOM seems to be appropriate for power flow studies of DSTATCOM. In steady state conditions, DSTATCOM is like a shunt reactive power source that can regulate the voltage magnitude of the bus where it is to be installed. We assume that bus i is a bus of the system with a load equal to PLi+jQLi. We can model DSTATCOM on bus i as a new PV bus j, added to bus i with its active power set to zero [43]. This model is illustrated in Fig. 6.
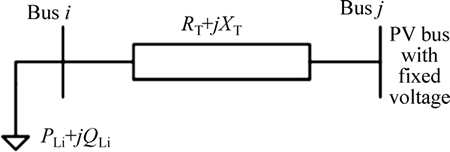
Fig. 6 DSTATCOM modeled in bus j
4 Cost function and problem formulation
The main objective is to find the optimal location of DSTATCOM, along with network constraints so as to minimize the total operational cost and reduce power loss under different loading conditions. Installation costs of DSTATCOM device and the cost of system operation, namely, energy loss cost, are combined to form the objective function to be minimized. Besides DFACTS devices, distribution loss can be minimized by DG installation, by the addition of shunt capacitors at weak buses and by changing the status of sectionalizing switches and determining appropriate tie switches which is possible by reconfiguration. In this work, the reconfiguration of distribution system beside DSTATCOM allocation is analyzed. The optimal allocation problem of DSTATCOM under reconfiguration can be formulated as [44]
 (14)
(14)
where C1(E) is the cost due to energy loss; C2(F) is the total investment cost of the DSTATCOM device; C(T) is the operational cost of the system.
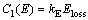 (15)
(15)
where kE is the energy cost per kWh, and Eloss is the network energy losses in a year that is calculated as Eloss=8760×loss load factor×Ploss. The loss load factor can be calculated as G=0.5F+0.5F2, where F is load factor [45].
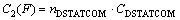 (16)
(16)
The active and reactive nodal power should be within the limits as follows:
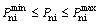 (17)
(17)
And
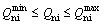 (18)
(18)
Again, these active and reactive nodal powers have to satisfy voltage magnitude constraints:
 (19)
(19)
The power flow equations between nodes i and j after incorporating DSTATCOM devices would appear as
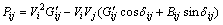 (20)
(20)
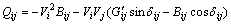 (21)
(21)
where G' and B' are the real and imaginary components of bus admittance matrix with the inclusion of DSTATCOM; G and B are the real and imaginary part of Ybus matrix without DSTATCOM. DSTATCOM placement at a weak node corresponds to reactive power injection at that node and accordingly there will be a change in reactive power flow in the line connected to that line. The Ybus matrix will also be modified with DSTATCOM in the following way [45]:
For j=1: nDSTATCOM
Shunt (DSTATCOM_pos(j))=sqrt(-1)* DSTATCOMvalue
End
where nDSTATCOM and DSTATCOMvalue are the numbers and values of DSTATCOM respectively.
In this way original Ybus matrix is modified into
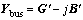 (22)
(22)
Then load flow is executed with this modified admittance matrix in evaluating the objective function for each individual population of generation in the cases of GA and fuzzy-GA.
In this study along with DSTATCOM allocation in distribution system, the reconfiguration process is also considered to minimize the energy loss and so minimize the operation cost of system, so the distribution system should be operated at a minimum cost subject to a number of constraints which must be considered in reconfiguration process.
1) Radial configuration
Distribution system in normal operation should be radial structure and have not islets and loops.
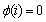 (23)
(23)
2) All loads served
During reconfiguration process not any of loads could be isolated.
Again, the voltage magnitude constraints must be considered as discussed further.
5 Weak node detection using fuzzy logic
The main objective of this work is the placement of DSTATCOM devices in optimal locations of the distribution power network. In this work, the locations of DSTATCOM’s are selected by calculating fuzzy membership of loss sensitivities of different buses in the standard IEEE 33-bus and 69-bus systems. Distribution feeder’s loss in power system is given as
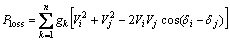 (24)
(24)
And the incremental distribution loss may be written as
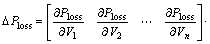
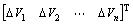 (25)
(25)
or
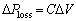 (26)
(26)
where 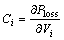 is the loss sensitivity of each bus.
is the loss sensitivity of each bus.
Fuzzy set is used to linearize objective function as
 (27)
(27)
where  and i=1, 2, …, n.
and i=1, 2, …, n.
The minimization of active power loss will take place when each Fi is as negative as possible which indicates that if Ci is negative and ΔVi will attain its maximum positive value. So, the more the Fi at a bus is, the more the voltage deviation at that bus is. A fuzzy based reasoning approach is developed by assuming the maximum negative value of Fi as Emi. A large value of Ci or less sensitivity at the ith bus indicates that the ith bus requires reactive power compensation by some means. Now fuzzy logic is used to determine membership values of these sensitivities and corrective action is to be taken according to the sensitivity observed at a particular bus. The membership of the objective function is expressed as follows:
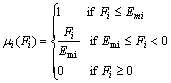 (28)
(28)
Steps involved for the implementation of sensitivity factor method to find optimal location for DSTATCOMs are presented as continue.
This problem is solved using the power flow algorithm and proposed method of Fig. 7 as follows:
Step 1: Run the base case load flow.
Step 2: Find the sensitivity factor by fuzzy logic and rank the sensitivity using determination of membership values of these sensitivities in descending order to form priority list.
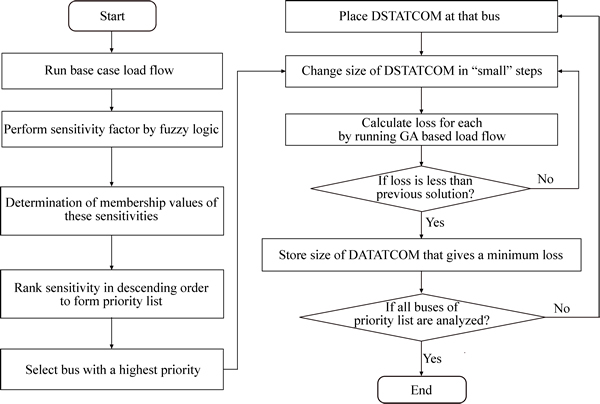
Fig. 7 Fuzzy based algorithm for optimal placement of DSTATCOM
Step 3: Select the bus with the highest priority and place DSTATCOM at that bus.
Step 4: Change the size of DSTATCOM in ‘‘small’’ steps and calculate loss for each by running load flow.
Step 5: Store the size of DSTATCOM that gives the minimum loss.
Step 6: Compare the loss with the previous solution. If loss is less than previous solution, store this new solution and discard previous solution.
Step 7: Repeat step 4 to step 6 for all buses in the priority list.
The main objective of this work is to minimize the overall operating cost under different condition by the installation of DSTATCOMs at the optimal locations in the distribution system.
Membership values of the bus sensitivities at different buses are determined according to the membership function as shown in Fig. 8. String representing control variables using fuzzy-GA is shown in Fig. 9. The following representation shows how the problem decision variables, i.e. tie switches and size of DSTATCOMs, are encoded inside a string in the algorithms, where si and cj denote the tie switch number of mesh i and the size of DSTATCOM at bus j, respectively.
6 Proposed approach
The purpose of this work is to minimize the total operating cost. Hence minimization of the objective function is a combinatorial, namely, only minimizing the energy loss will not serve the purpose, and simultaneously cost of the total numbers of DSTATCOM has to be considered.
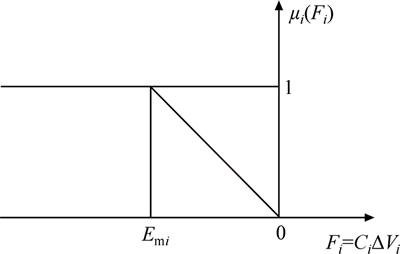
Fig. 8 Fuzzy membership functions
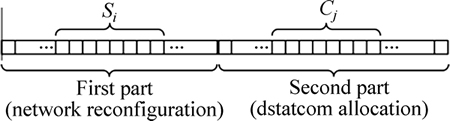
Fig. 9 Strings representing the control variables for Fuzzy-GA
After detection of weak buses by fuzzy approach, the optimal setting of power system, i.e., reconfiguration variables along with the sizes of DSTATCOMs, is done by genetic algorithm. The proposed method is termed as fuzzy-GA. The other way of weak bus detection is by modal analysis and after detecting the weak buses by this method the optimal setting of the power system can be done by GA. This combined method is the approach with which the result of the proposed approach is compared. The main steps of the GA algorithm are given [46]:
Genetic algorithm (GA) is an optimization algorithm based on the mechanics of natural selection and genetics. GA consists of three main operators- reproduction, crossover and mutation. It initializes a population of solution string called chromosomes. GA starts with random generation of initial population and then genetic operators are performed until the best solution is obtained. Genetic algorithm (GA) technique determines the optimal sizes of the DSTATCOMs to be connected with the existing system to maximize the system performance as the location of devices is already determined by power flow. DSTATCOMs control the reactive injection at buses. In addition, a combination of appropriate tie switches along with the optimal number of DSTATCOMs is controlled. Reconfiguration of distribution systems is achieved by changing the status of the switches in the loops. A loop in distribution network consists of a tie switch and some sectionalizing switches. A certain switch of each loop is then selected to open to make the network radial, and the selected switch naturally becomes a tie switch. The network reconfiguration problem is identical to the problem of selection of an appropriate tie switch for each loop so that the objective function could be minimized. As a whole all these variables are to be optimized by genetic algorithm.
As shown in Fig. 10, the following steps are used for the solution of objective function using GA.
1) Initialization: Generate random population of n chromosomes.
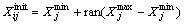 (29)
(29)
where i=1, 2, …, Np; j=1, 2, …, D; 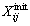 is the initial population of size Np; rand is the random number
is the initial population of size Np; rand is the random number 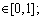 D is the total number of variables;
D is the total number of variables; 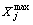 and
and 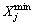 are the maximum and minimum values of a control variable, respectively. The chromosomes are represented in the form of a string
are the maximum and minimum values of a control variable, respectively. The chromosomes are represented in the form of a string
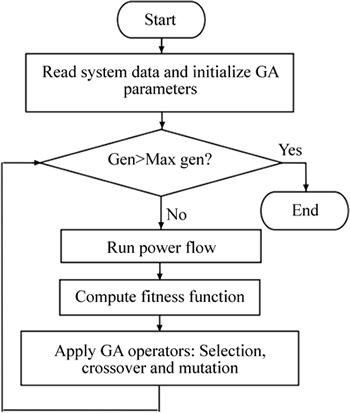
Fig.10 Flowchart of GA implementation
2) Fitness: Evaluate the objective function of each chromosome in the initial population.
3) New population: Create a new population by repeating following steps until the new population is complete.
(i) Selection: Select two parent chromosomes from a population according to their fitness (the better fitness, the bigger chance to be selected).
(ii) Crossover: Crossover between two randomly selected chromosomes from the current population is done with a probability close to 1(here 0.8) to form a new offspring. The crossover operation between two strings will take place,  and
and 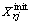 (here r is the randomly generated integer whose maximum value is Np, the number of population, and r≠i).
(here r is the randomly generated integer whose maximum value is Np, the number of population, and r≠i).
(iii) Mutation: Mutation with a specific probability (very low) completes one genetic cycle and strings of the same population with improved qualities are produced in the next generation.
4) Use new generated population for a further run of algorithm.
5) The entire procedure from step 1 to step 4 is repeated as discussed above till satisfactory result is obtained.
7 Simulation and results
Two standard sample distribution networks are discussed to show the effectiveness of this combinatorial optimization technique. Examined IEEE networks have 33-bus and 69-bus systems that work at 12.66 kV and have radial structure [47, 48]. The single-line diagrams are shown in Figs. 11 and 12, respectively. Line data and load data of study systems are given in Refs. [21, 49]. As shown in Fig. 11, the first test system, the base configuration of the system, is having a single supply point with 33 buses, 3 laterals, 37 branches, 5 loops or tie switches (switches 33-37) which are kept normally open, as shown in dotted lines and are closed only during fault condition to maintain continuity of supply or can be closed to change circuit resistance to reduce losses. The total real power for base configuration is 3715 kW, 2300 kVar with a real power loss of 202.67 kW.
As shown in Fig. 12, a typical 69-bus distribution system is used as the second case-study. The system consists of 74 branches as well as five tie switches (switches 70-74), while the load is assumed to be constant. The system voltage is 12.66 kV and total system load is 3802 kW and 2694 kVar. The data of 69-bus system are available in Ref. [49].
The results are compared through the following cases.
Case 1: The radial distribution system without reconfiguration and without connection of DSTATCOM (Base case).
Case 2: DSTATCOM allocation without consideration of reconfiguration process (DSTATCOM allocation only).
Case 3: Both the reconfiguration and connection of DSTATCOMs have been applied in the system. Optimal allocation of DSTATCOMs first has been applied and then reconfiguration is performed. They are done separately.
Case 4: Simultaneous operation of reconfiguration and connection of DSTATCOMs.
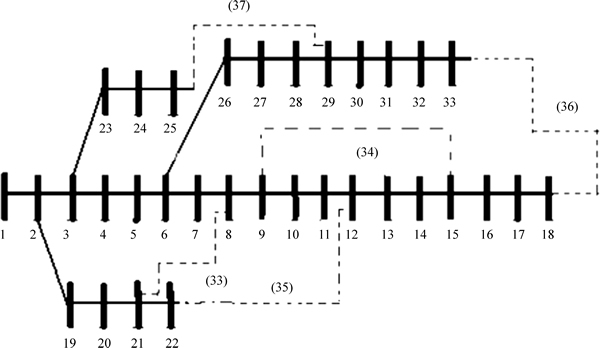
Fig. 11Typical 33-bus distribution system
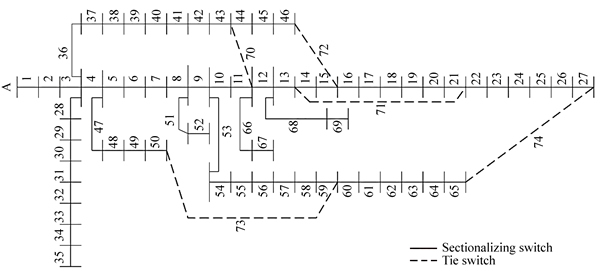
Fig. 12 Typical 69-bus distribution system
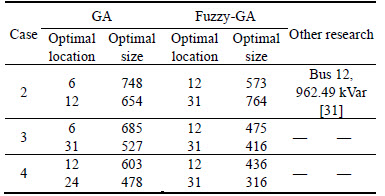
It is already mentioned that the determination of weak nodes for DSTATCOM installation is one of the primary and important task of the proposed work. The weak nodes for the DSTATCOM placement are determined by fuzzy membership values of loss sensitivities at buses. The five buses having higher membership values of loss sensitivities of 33-bus test system are listed in Table 1. Based on the fuzzy membership function, bus numbers 12, 31, 6, 18 and 22 are found as candidate buses for the placement of DSTATCOMs having higher membership values. Since the installation of two DSTATCOM units with nominal capacity of 800 kvar is considered in this work, so in IEEE 33-bus system, the best locations of DSTATCOM are bus No.12 and bus No.31.
Table 1 Membership function of different buses of 33-bus test system
The convergence characteristics of the best results for t by two methods on 33-bus system are shown in Fig. 13. The fuzzy-GA can find better solution in less iteration and is more efficient than another method.
The results of two algorithms for 33-bus system are shown in Table 2.
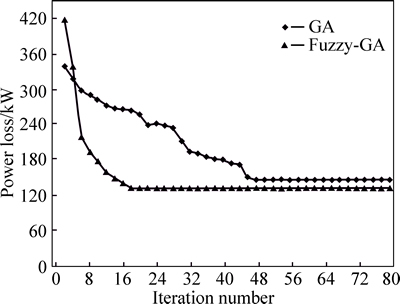
Fig. 13 Comparison of convergence characteristics of power loss for 33-bus system
Table 2 Optimal results of DSTATCOM allocation in 33-bus system
The open switches for the optimal solution found by two methods are shown in Table 3. GA opened switches [9-14-28-32-33] for case 3 and [10-14-28-31-36] for case 4; while fuzzy-GA opened switches [10-14-28-31- 33] for case 3 and [9-14-27-33-36] for case 4. So the hybrid method could be applied to the distributed reconfiguration well.
Voltage profile of 33-bus (for base case and three considered cases) is shown in Fig. 14. Through simultaneous reconfiguration with DSTATCOM allocation (case 4), voltage magnitude of 33-bus had been greatly improved than initial network with DSTTCOM (case 2) or than initial network with reconfiguration and DSTATCOM allocation as separately (case 3).
Table 3 Optimal results of tie switches in 33-bus system

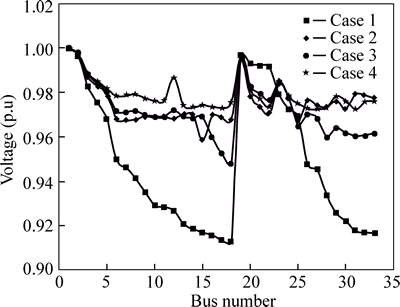
Fig.14 Comparison of voltage magnitude for 33-bus system
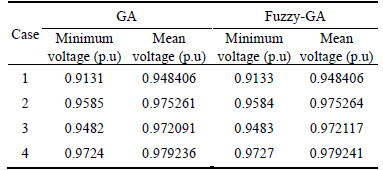
Compare with all cases in Fig. 14, we can find that the buses which inject DSTATCOM have the improvement in voltage magnitude. For example, the voltage of 18-bus improves from 0.9131p.u in the case 1 to 0.9727p.u in the case 4. The detail of voltage profile analysis of all buses of current test system in terms of the minimum voltage and mean voltage is listed in Table 4.
Table 4 Comparative analysis of voltage profile in in 33-bus system
After reconfiguration, the real power loss is reduced from 202.68 kW to 168.45 kW (case 2); through reconfiguration and DSTATCOM allocation separately, the real power loss is reduced to 156.34 kW. Using simultaneous reconfiguration with DSTATCOM allocation the real power loss is reduced to 132.87 kW. This result is listed in Table 5.
Table 5 Comparative analysis of active power loss in 33 bus system

Figure 15 shows the active loss reduction of proposed two methods (GA and fuzzy-GA) for different cases in the presence of DSTATCOM and reconfiguration in a 33-bus distribution test system. The hybrid proposed method (fuzzy-GA) shows more reduction in power losses compared with GA method.
A comparative study on the operating cost of the 33-bus system without and with DSTATCOM devices under different case studies for all techniques is shown in Table 6.
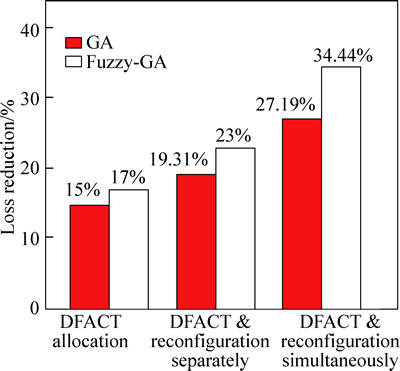
Fig. 15 Comparison of GA and GA-fuzzy methods in loss reduction for different cases in 33-bus system
From the comparative study on different techniques, it is found that the best result both in the basis of loss reduction and operating cost reduction of 33-bus system is achieved using fuzzy based genetic algorithm as seen from Tables 5 and 6.
Table 6 Comparative analysis of operating costs in 33-bus system

The weak nodes for the DSTATCOM placement are determined by fuzzy membership values of loss sensitivities at buses. The six buses having higher membership values of loss sensitivities of 69-bus test system are listed in Table 7. Based on the fuzzy membership function, bus numbers 16, 27, 31, 43, 52 and 61 are found as candidate buses for the placement of DSTATCOMs. The installation of two DSTATCOM units with nominal capacity of 800 kVar is considered in this study, so in IEEE 69-bus system, the best locations of DSTATCOM are bus No. 27 and bus No. 61.
Figure 16 shows the convergence graph of power loss using GA and fuzzy-GA with 69-bus system. This figure indicates that fuzzy-GA converges better than another existing method.
Table 8 gives the optimal location and optimal sizes of DSTATCOMs for three cases (cases 2, 3, and 4) of 69- bus test system. It is observed that the fuzzy-GA gives the more accurate results than another method. Also the comparison of results of proposed method in other papers for existing cases (cases 2 and 4) is presented in Table 8. The results of proposed method in cases 2 and 4 are nearly similar to obtained results in Refs. [29, 31] as listed in the last column of Table 8.
Table 7 Membership function of different buses of 69-bus test system
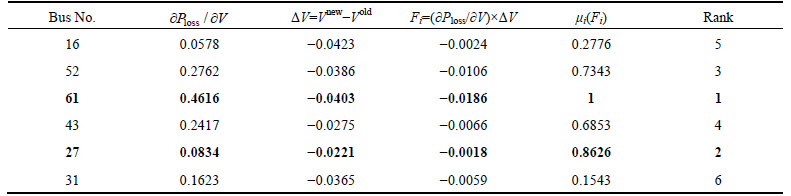
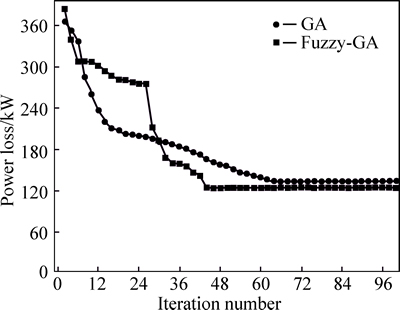
Fig. 16 Comparison of convergence characteristics of power loss for 69-bus system
The various switching statuses using proposed method for different cases are given in Table 9. As shown in Table 9, it is observed that the power loss is a minimum value when the switches [70-69-50-47-13] are open in 69-bus system while reconfiguration and DSTATCOM allocation are considered simultaneously.
The network bus voltage profiles for different cases are compared in Fig. 17. Compare with all cases in Fig. 17, we can find that the buses which inject DSTATCOM have the improvement in voltage magnitude. For example, the voltage of 60-bus system improves from 0.9197p.u in the case 1 to 0.9523 p.u in the case 4. The detail of voltage profile analysis of all buses of current test system in terms of minimum voltage and mean voltage is listed in Table 10.
As listed in Table 10, in the case 1 (base case), the minimum bus voltage of the system versus per unit is 0.9091p.u, which occurs at bus 65, while using only DSTATCOM allocation (case 2) the minimum bus voltage of the system is 0.9399p.u, which occurs at bus 64. Through combination of DSTATCOM allocation and reconfiguration, the minimum bus voltage of the system is 0.9361p.u, which occurs at bus 65 when two processes are performed separately and the minimum value is 0.9367p.u, which occurs at bus 61 when two processes are performed simultaneously. This indicates that in case 4 the voltage profile has great improvement.
Power loss analysis of 69-bus system is presented in Table 11. The operation of the system by using proposed method in the initial case (case 1) shows that the network of 69-bus system runs without the presence of reconfiguration and DSTATCOM. The network has given the initial total power loss of 225 kW through five initial open switches 70, 71, 72, 73 and 74.
Figure 18 shows the active loss reduction of proposed two methods (GA and fuzzy-GA) for different cases in the presence of DSTATCOM and reconfiguration in a 69-bus distribution test system. The hybrid proposed method (Fuzzy-GA) shows more reduction in power losses compared with GA method. As shown in Fig. 18, while in case 2 where the only DSTACOM is employed in the network of 69-bus system, the power loss reduction has been improved by 25% (225 kW to 168.72 kW). In this case, reconfiguration is taken out so that we can clearly observe the impact of DSTATCOM. Meanwhile, in case 3 where the network of 69-bus system is operated by reconfiguration and DSTATCOM allocation separately the total power loss is reduced by 83.25 kW or 37% (from 225 kW to 141.75 kW). The network condition of case 4 study is almost identical to case 3 except this time that both reconfiguration and DSTATCOM are being organized simultaneously. The total power loss is reduced by 102.22 kW or 45.43% (from 225 kW to 122.78 kW).
A comparative study of the operating cost of the 69-bus system without and with DSTATCOM devices under different case studies for all techniques is shown in Table 12.
From the comparative study of different techniques,it is found that the best result in the basis of loss reduction and operating cost reduction of 69-bus system is achieved using fuzzy based genetic algorithm as listed Tables 11-12.
Table 8 Optimal results of DSTATCOM allocation in 69-bus system
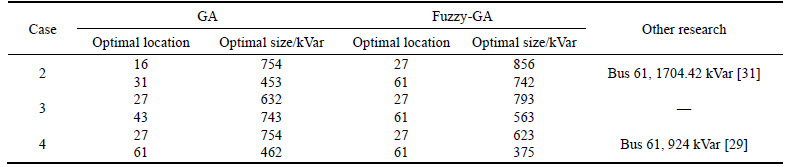
Table 9 Optimal results of tie switches in 69-bus system

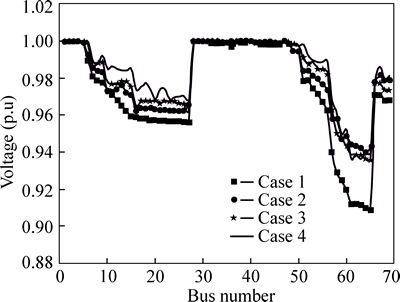
Fig.17 Comparison of voltage magnitude for 69-bus system
Table 10 Comparative analysis of voltage profile in 69-bus system
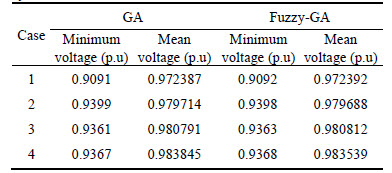
Table 11 Comparative analysis of active power loss in 69-bus system
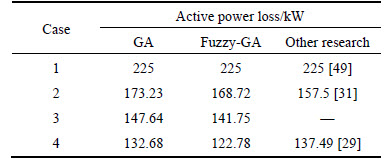
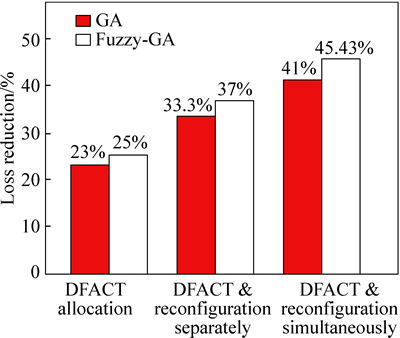
Fig. 18 Comparison of GA and GA-fuzzy methods in loss reduction for different case studies in 69-bus system
Table 12 Comparative analysis of operating costs in 69-bus system

8 Conclusions
1) This work deals with distribution system feeder reconfiguration considering a shunt type DFACTS device, DSTATCOM with an objective of minimizing real power loss and operating cost.
2) The fuzzy membership function of loss sensitivity is used to select the weakest nodes in the power system for the placement of DSTATCOM and the optimal parameter sizes of DSTATCOM devices along with optimal selection of tie switches in reconfiguration process are found by genetic Algorithm (GA).
3) Presence of DSTATCOM and network reconfiguration as simultaneous enables the electrical utilities to take other advantages, such as power quality improvement, voltage stability, system load ability and stability.
4) Simulation results concluded that the combinatorial method using DSTATCOM and reconfiguration is preferable to reduce power losses to 34.44 for 33-bus system and to 45.43% for 69-bus system.
5) Also it is seen that simultaneous implementation of DSTATCOM and reconfiguration can improve the voltage profile of system so that the minim voltage of system increases to 0.9727p.u in the first case study and to 0.9368pu for the second case study.
6) Simulation results verified that total saving cost is considerably increased when simultaneous implementation of DSTATCOM and reconfiguration are considered. Simulation results concluded that the combinatorial method using fuzzy and GA leads to better results compared to GA and previous studies.
Acknowledgments
This study was supported by Borujerd Branch, Islamic Azad University Iran. The authors would like to acknowledge staffs of University.
References
[1] ABDELAZIZ A, OSAMA R, EL-KHODARY S. Reconfiguration of distribution systems for loss reduction using the hyper-cube ant colony optimization algorithm [J]. IET Generation Transmission Distribution, 2012, 6(2): 176-187.
[2] CHANDRAMOHAN S, NARESH A, KUMUDINI R P, VENKATESH DEVI B. Operating cost minimization of a radial distribution system in a deregulated electricity market through reconfiguration using NSGA method [J]. International Journal of Electrical Power and Energy Systems, 2010, 32: 126-132.
[3] ESMAEILIAN H R, FADAEINEDJAD R. Distribution system efficiency improvement using network reconfiguration and capacitor allocation [J]. International Journal of Electrical Power and Energy Systems, 2015, 64: 457-468.
[4] BROWN R E. Distribution system reliability assessment and reconfiguration optimization [C]// Transmission and Distribution Conference and Exposition Conference. IEEE, 2011: 994-999.
[5] SHIRMOHAMADDI D, HONG H W. Reconfiguration of electric distribution networks for resistive line losses reduction [J]. IEEE Transaction Power Delivery, 1989, 4(2): 1492-1498.
[6] KASHEM M A, GANAPATHY V, JAMSON G B. Network reconfiguration for enhancement of voltage stability in distribution networks [J]. IEE Proceedings Generation Transmission Distribution, 2000, 147(3): 171-175.
[7] SAHOO N C, PRASAD K. Fuzzy genetic approach for network reconfiguration [J]. International Journal of Energy Conversion Management, 2006, 47(18): 3288-3306.
[8] PRASAD K, RANJAN R, SAHOO N C, CHATURVEDI A. Optimal reconfiguration of radial distribution systems using a fuzzy mutated genetic algorithm [J]. IEEE Transaction Power Delivery, 2005, 20(2): 1211-1213.
[9] VENKATESH B, RANJAN R. Optimal radial distribution system reconfiguration using fuzzy adaptation of evolutionary programming [J]. International Journal of Electrical Power and Energy Systems, 2003, 25: 775-780.
[10] VENKATESH B, RANJAN R, GOOI H B. Optimal reconfiguration of radial distribution systems for maximize the load-ability [J]. IEEE Transaction Power System, 2004, 19(1): 260-266.
[11] DAS D. Optimal placement of capacitors in radial distribution system using a fuzzy-GA method [J]. International Journal of Electrical Power and Energy Systems, 2008, 30(6, 7): 361-367.
[12] MENDOZA F, BERNAL-AGUSTIN J L, DOMINGUEZ- NAVARRO J A. NSGA and SPEA applied to multi objective design of power distribution systems [J]. IEEE Transaction Power System, 2006, 21(4): 1938-1945.
[13] DAS D. Reconfiguration of distribution system using fuzzy multi- objective approach [J]. International Journal of Electrical Power and Energy Systems, 2006, 28(5): 331-338.
[14] AMANULLA B, CHAKRABARTI S, SINGH S. Reconfiguration of power distribution systems considering reliability and power loss [J]. IEEE Transaction Power Delivery, 2012, 27(2): 918-926.
[15] KAVOUSI-FARD A, AKBARI-ZADEH M. Reliability enhancement using optimal distribution feeder reconfiguration [J]. Neurocomputing, 2013, 106(1): 1-11.
[16] MENDOZA J, LOPEZ M, COELLO C, LOPEZ E. Microgenetic multi objective reconfiguration algorithm considering power losses and reliability indices for medium voltage distribution network [J]. IET Generation Transmission Distribution, 2009, 3(9): 825-840.
[17] MAZZA A, CHICCO G, RUSSO A. Optimal multi-objective distribution system reconfiguration with multi criteria decision making-based solution ranking and enhanced genetic operators [J]. International Journal of Electrical Power and Energy Systems, 2014, 54(1): 255-267.
[18] WU Y, LEE C, LIU L, TSAI S. Study of reconfiguration for the distribution system with distributed generators [J]. IEEE Transaction Power Delivery, 2010, 25(3): 1678-1685.
[19] RAJARAM R, SATHISH KUMAR K, RAJASEKAR N. Power system reconfiguration in a radial distribution network for reducing losses and to improve voltage profile using modified plant growth simulation algorithm with Distributed Generation (DG) [J]. Energy Reports, 2015, 1: 116-122.
[20] RAO S, RAVINDRA K, SATISH K. Power loss minimization in distribution system using network reconfiguration in the presence of distributed generation [J]. IEEE Transaction Power System, 2013, 28(1): 317-325.
[21] GUAN Wan-lin, TAN Yang-hong, ZHANG Hai-xia, SONG Jian-li. Distribution system feeder reconfiguration considering different model of DG sources [J]. International Journal of Electrical Power and Energy Systems, 2015, 68: 210-221.
[22] OLAMAEI J, NIKNAM T, GHAREHPETIAN G. Application of particle swarm optimization for distribution feeder reconfiguration considering distributed generators [J]. Applied Mathematics and Computing, 2008, 201(1, 2): 575-586.
[23] ESMAEILIAN H R, FADAEINEDJAD R. Distribution system efficiency improvement using network reconfiguration and capacitor allocation [J]. International Journal of Electrical Power and Energy Systems, 2015, 64: 457-468.
[24] FARAHANI V, VAHIDI B, ABYANEH H. Reconfiguration and capacitor placement simultaneously for energy loss reduction based on an improved reconfiguration method [J]. IEEE Transaction Power Systems, 2011, 2(5): 621-631.
[25] OLIVEIRA L, CARNEIRO S, de OLIVEIRA E, PEREIRA J, SILVA I, COSTAI J. Optimal reconfiguration and capacitor allocation in radial distribution systems for energy losses minimization [J]. International Journal of Electrical Power and Energy Systems, 2010, 32(8): 840-848.
[26] CHANG C. Reconfiguration and capacitor placement for loss reduction of distribution systems by ant-colony search algorithm [J]. IEEE Transaction Power System, 2008, 23(4): 1747-1755.
[27] CHAN K, KARA A, DAEHLER P, GUAY J, TINGGREN R. Innovative system solutions for power quality enhancement [J]. IEEE Transaction Power Delivery, 1999, 3: 4-12.
[28] GHOSH A, LEDWICH G. Power quality enhancement using custom power devices [M]. New York: Kluwer Academic Publishers, 2002.
[29] JAZEBI S, HOSSEINIAN S.H, VAHIDI B. DSTATCOM allocation in distribution networks considering reconfiguration using differential evolution algorithm [J]. Energy Conversion and Management, 2011, 52: 2777-2783.
[30] BAGHERI TOLABI H, MOHD HASAN A, RIZWAN M. Simultaneous reconfiguration, optimal placement of DSTATCOM, and photovoltaic array in a distribution system based on fuzzy-ACO approach [J]. IEEE Transactions on Sustainable Energy, 2015, 6(1): 210-218.
[31] TAHER S A, AFSARI S A. Optimal location and sizing of DSTATCOM in distribution systems by immune algorithm [J]. International Journal of Electrical Power and Energy Systems, 2014, 60: 34-44.
[32] BAGHERINASAB A, ZADEHBAGHERI M, SAIFULNIZAM A K H, GANDOMKAR M, NAZIHA A A. Optimal placement of D-STATCOM using hybrid genetic and ant colony algorithm to losses reduction [J]. IJAPE: International Journal of Applied Power Engineering, 2013, 2(2): 53-60.
[33] CHAITHRA C, PADMAJA K. Optimum placement of D-STATCOM using firefly algorithm for enhancing power quality [J]. IJARCCE: International Journal of Advanced Research in Computer and Communication Engineering, 2015, 4(6): 20-24.
[34] SALMAN N, MOHAMED A, SHAREEF H. Reliability improvement in distribution systems by optimal placement of DSTATCOM using binary gravitational search algorithm [J]. Przegl  Elektrotechniczny: Electrical Review, 2012, 88: 295-299.
Elektrotechniczny: Electrical Review, 2012, 88: 295-299.
[35] DEVI S, GEETHANJALI M. Optimal location and sizing determination of distributed generation and DSTATCOM using particle swarm optimization algorithm [J]. International Journal of Electrical Power and Energy Systems, 2014, 62: 562-570.
[36] DEVABALAJI K R, RAVI K. Optimal size and sitting of multiple DG and DSTATCOM in radial distribution system using bacterial foraging optimization algorithm [J]. Ain Shams Engineering Journal, 2015, 24: 124-129.
[37] BLAZIC B, PAPIC I. A new mathematical model and control system of DSTATCOM for operation under unbalanced conditions [J]. Electric Power System Research, 2004, 72(3): 279-287.
[38] HINGORANI N. Introducing custom power [J]. IEEE Spectrum, 1995, 32(6): 41-48.
[39] NILSSON S. Special application consideration for custom power systems [C]// IEEE Conference Power Engineering Society. New York: IEEE, 1999, 2: 1127-1130.
[40] GHOSH S, DAS D. Method for load-flow solution of radial distribution networks [J]. IEE Proceedings Generation Transmission Distribution, 1999, 146(6): 641-648.
[41] HOSSEINI M, SHAYANFAR HA, FOTUHI M. Modeling of series and shunt distribution facts devices in distribution load flow [J]. Journal Electrical System, 2008, 4(4): 1-12.
[42] ACHA E, FUERTE-ESQUIVEL C R, AMBRIZ-PEREZ H, ANGELES-CAMACHO C. FACTS modeling and simulation in power networks [M]. New York: Wiley, 2004.
[43] YANG Z, SHEN C, CROW M L, ZHANG L. An improved STATCOM model for power flow analysis [C]// Power Engineering Society Summer Meeting, 2000, 2: 1121-1126.
[44] BHATTACHARYYA B, KUMAR GUPTA V. Fuzzy based evolutionary algorithm for reactive power optimization with FACTS devices [J]. International Journal of Electrical Power and Energy Systems, 2014, 61: 39-47.
[45] TABATABAEI S M, VAHIDI B. Bacterial foraging solution based fuzzy logic decision for optimal capacitor allocation in radial distribution system [J]. Electric Power Systems Research, 201, 81: 1045-1050.
[46] ZHOU Ji-cheng, YAN Jian-wei, TIAN Li-xia. Influence of rapid process on the structure and properties of Ni-Cr thin-films fabricated by ion beam sputtering [J]. Journal of Central South University: Science and Technology, 2006, 37(5): 837-840. (in Chinese)
[47] BARAN M E, WU F F. Optimal capacitor placement on radial distribution systems [J]. IEEE Transaction Power Delivery, 1989, 4(1): 725-732.
[48] BARAN M E, WU F F. Network reconfiguration in distribution systems for loss reduction and load balancing [J]. IEEE Transaction Power Delivery, 1989, 4(2): 1401-1407.
[49] SAHOO N C, PRASAD K. A fuzzy genetic approach for network reconfiguration for enhance voltage stability in radial distribution systems [J]. Energy Conversion and Management, 2006, 47: 3288-3306.
(Edited by YANG Hua)
Cite this article as: Mohammad Mohammadi, Mahyar Abasi, A. Mohammadi Rozbahani. Fuzzy-GA based algorithm for optimal placement and sizing of distribution static compensator (DSTATCOM) for loss reduction of distribution network considering reconfiguration [J]. Journal of Central South University, 2017, 24(2): 245-258. DOI: 10.1007/ s11171-017-3425-4.
Received date: 2015-11-03; Accepted date: 2016-01-30
Corresponding author: Mohammad Mohammadi, PhD; Tel: +98-09188607414; E-mail: mohammadi.m@iaub.ac.ir

