蛇形热轧中轧制参数对7075铝合金厚板变形分布的影响
来源期刊:中国有色金属学报(英文版)2014年第7期
论文作者:张涛 吴运新 龚海 郑细昭 蒋绍松
文章页码:2150 - 2156
关键词:有限元仿真;7075铝合金;蛇形轧制;剪切变形;异速比;错位量;压下量
Key words:finite simulation; 7075 aluminum alloy; snake rolling; shear strain; velocity ratio; offset distance; pass reduction
摘 要:介绍了蛇形轧制的实现方式。运用数值模拟方法,在Deform 3D上分析单道次轧制过程中蛇形轧制和对称轧制7075铝合金厚板的流动速度及应力应变分布情况,分析异速比、上下轧辊错位量和压下量对蛇形轧制变形区内轧板等效应变和剪切应变的影响规律。结果表明:蛇形轧制中,由于下辊速度快,轧板下层金属流动比上层快,蛇形轧制中轧板下层等效变形大于上层,且随着异速比的增大,上下层金属变形差距增大;对称轧制中厚板心部的剪切应变几乎为0,蛇形轧制中由于有“搓轧区”的存在,厚板心部的剪切应变远大于对称轧制的,且随着异速比的增加和错位量的增加,轧板心部的剪切变形增大。这种附加的剪切变形有利于使变形向厚板心部渗透,从而改善厚板高向变形的不均匀性。
Abstract: The realization way of snake rolling was introduced. Flow velocity, strain and stress distribution of 7075 aluminum alloy plate during snake rolling and symmetrical rolling were analyzed in Deform 3D. Effects of velocity ratio, offset distance between two rolls and pass reduction on the distribution of equivalent strain and shear strain were analyzed. The results show that flow velocity and equivalent strain on the lower layer of the plate are larger than those of the upper layer because of the larger velocity of the lower roll and the gap is increased with the increase of velocity ratio and pass reduction. The shear strain of rolling direction in the center point is almost zero during symmetrical rolling, while it is much larger during snake rolling because of the existence of rub zone. The shear strain is increased with the increase of velocity ratio, offset distance and pass reduction. This additional shear strain is beneficial to improve the inhomogeneous strain distribution.
Trans. Nonferrous Met. Soc. China 24(2014) 2150-2156
Tao ZHANG1,2, Yun-xin WU1,2, Hai GONG1,2, Xi-zhao ZHENG1,2, Shao-song JIANG1,2
1. School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China;
2. State Key Laboratory for High Performance Complex Manufacturing, Central South University, Changsha 410083, China
Received 17 October 2013; accepted 8 April 2014
Abstract: The realization way of snake rolling was introduced. Flow velocity, strain and stress distribution of 7075 aluminum alloy plate during snake rolling and symmetrical rolling were analyzed in Deform 3D. Effects of velocity ratio, offset distance between two rolls and pass reduction on the distribution of equivalent strain and shear strain were analyzed. The results show that flow velocity and equivalent strain on the lower layer of the plate are larger than those of the upper layer because of the larger velocity of the lower roll and the gap is increased with the increase of velocity ratio and pass reduction. The shear strain of rolling direction in the center point is almost zero during symmetrical rolling, while it is much larger during snake rolling because of the existence of rub zone. The shear strain is increased with the increase of velocity ratio, offset distance and pass reduction. This additional shear strain is beneficial to improve the inhomogeneous strain distribution.
Key words: finite simulation; 7075 aluminum alloy; snake rolling; shear strain; velocity ratio; offset distance; pass reduction
1 Introduction
Aluminum alloys have been widely used in aerospace and marine vessels because of their low density, high strength, good formability and damage resistance. Aluminum alloy plates with high strength and high toughness, are widely used in main frames, wing boxes, stringers and other key components of aircraft. 70%-81% of the materials used in the civilian aircraft is aluminum alloy [1] and it makes about 1400 pounds lighter than the designed weight in B777. Hot rolling is a critical process of manufacture of aluminum alloy plate with high performance. Large deformation of the plate can be achieved and casting defects can be eliminated in hot rolling. Studies show that the structure in the center portion of thick plate will be totally changed from cast structure to processed structure when deformation rate of hot rolling reaches more than 75% for aluminum alloy [2]. Therefore, to produce a plate with thickness of 250 mm, the original thickness of the billet must be more than 1000 mm. However, such a large thick billet cannot be prepared using the existing technology and equipment and cannot be rolled by the largest existing mill. Symmetrical rolling causes large deformation on the surface of the thick plates and small deformation in the central portion, which will result in inhomogeneous deformation in the height direction and coarse grains in the central portion.
In this study, we focus on a new technique of snake rolling to solve severe inhomogeneous strain distribution of aluminum alloy plate during symmetrical rolling, which has been used in 4064 hot rolling mill in Germany [3]. Aluminum alloy plate with thickness of 250 mm and homogeneous performance in height direction can be prepared from a square billet with thickness of 500-600 mm by snake rolling [4]. With the development of manufacture of domestic aircraft, thicker aluminum alloy plates (even to 200 mm) with homogeneous properties are in great need. A new method of snake rolling could be used to provide theory basis and technical support for independent preparation of high-performance aluminum thick plates.
The stress-strain field, microstructure evolution and mechanical properties of rolled plate were discussed in rolling process [5-7]. MOVSAVI et al [8] studied the effect of speed ratio on distribution of normal stress and shear stress, shear zone length, curvature of rolled plate, rolling force and moment in asynchronous rolling. ZUO et al [9] and YUAN and SUN [10] studied the effects of pass reduction and speed ratio on shear strain distribution in asynchronous rolling. LIU and KAWALLA [11] studied effects of different diameter ratios with the same angular velocity between upper and lower rolls of asymmetrical rolling on microstructure and rolling force with austenitic steels and smaller average grain size can be generated when the diameter ratio is 1.05. Grain refinement and the texture evolution of rolled plate were studied and compared with conventional rolling [12-16]. Many theoretical models of calculation on rolling force and curvature of plate in asymmetrical rolling were established and they had good agreement with experimental data [17-24].
However, few studies have been conducted on effects of rolling parameters of snake rolling on the distribution of strain and stress, especially on the variation of shear strain, as shear strain is an important factor to the inhomogeneous strain distribution of thick plate. In this study, flow velocity, strain and stress distribution of aluminum alloy thick plate during snake rolling and symmetrical rolling were analyzed. Also, effects of different velocity ratios, offset distances between upper and lower roll and pass reductions on the distribution of equivalent strain and shear strain of thick plate were analyzed.
2 Realization way of snake rolling
Figure 1 shows the schematic of different rolling methods. Figure 1(a) represents symmetrical rolling, velocities of two work rolls are the same, which results in equal neutral angle. In symmetrical rolling, the plate is only subjected to compression stress. Figure 1(b) represents asynchronous rolling, the lower roll has a larger velocity and a smaller neutral angle. A “rub zone” where friction forces are in opposite direction on the upper and lower surface is formed in the deformation zone between two neutral points of two rolls. Snake rolling is achieved by an offset distance of upper roll in outlet direction on the basis of asynchronous rolling. The plate is subjected to not only compression strain in the vertical direction, but also shear strain in the horizontal direction in “rub zone”. Shear strain is beneficial to penetrate the deformation into the center portion of the plate and improve the inhomogeneous strain distribution in the height direction. The plate will bend to the direction of slower roll in asynchronous rolling and it may affect the following passes. In snake rolling, a force or moment will be applied to the plate in the opposite direction of bending by an offset distance of the slower roll in outlet direction. As a result, the plate is not only subjected to a large shear strain, but also can be processed smoothly in the following passes with a small curvature in snake rolling.

Fig. 1 Schematic of different rolling methods
3 Numerical modeling
3.1 Model description
Table 1 Parameters for rolled plate

Table 2 Parameters for roll

Single-pass rolling models of symmetrical rolling and snake rolling were established in Deform 3D. In this study, effects of velocity ratio, offset distance between upper and lower roll and pass reduction on the distribution of equivalent strain and shear strain of thick plate were analyzed. The parameters for rolled plate and rolls are shown in Tables 1 and 2, respectively. The material of roll was 4Cr5MoSiV1 and rolls were defined as rigid bodies because the deformation of rolls in hot rolling is so small that it can be neglected. The material of the plate was 7075 aluminum alloy, its flow stress model [25] is defined as

 (1)
(1)
3.2 Boundary condition
3.2.1 Heat transfer due to convection and radiation
The free surfaces of the plate may exchange heat with the environment by means of convection and radiation. The mathematical expression is defined as
q=(hr+hc)(T-Te) (2)
where hr and hc represent heat transfer coefficients due to radiation and convection, respectively; T and Te represent temperatures of plate and environment, respectively. In this study, the total heat transfer coefficient due to convection and radiation is defined as 5 W/(m2·K).
3.2.2 Heat transfer due to contact
There is large heat transfer between plate and roll in rolling process, it is defined as

where hl represents heat transfer coefficient due to contact Tr represent temperature of work roll. Heat transfer due to contact is a complex process and it is connected with surface topography, temperature and pressure during hot rolling. In this study, the heat transfer coefficient due to contact is defined as 10 kW/(m2·K).
3.2.3 Friction boundary conditions
As the normal stress is very large in hot rolling, using the Coulomb friction model may bring large error. In general, the shear friction model based on the shear stress is widely used. The mathematical expression is defined as
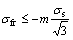 (4)
(4)
where σfr and σs represent shear stress and equivalent stress respectively; m represents the friction coefficient.
4 Results and discussion
Single-pass rolling models were established to analyze the difference of flow velocity and strain distribution between snake rolling and symmetrical rolling. The pass reduction is 45 mm, offset distance between two work rolls is 30 mm, the velocity of upper roll is 3 m/min and the velocity ratio is 1.20.
4.1 Comparison of flow velocity between symmetrical rolling and snake rolling
Figure 2 shows flow velocity distribution in height direction of the plate in symmetrical rolling and snake rolling. The flow velocity distribution of symmetrical rolling is symmetrical, and the velocity of the subsurface (about 1/8 thickness of the surface) is larger than that of the surface. The velocity of the surface point is slower because the friction force is larger, which hinders the metal flow on the surface. In snake rolling, flow velocity in the lower layer is much larger than that of the upper layer because of larger velocity of the lower roll. As can be seen, the flow velocity in snake rolling is larger than that in symmetrical rolling.

Fig. 2 Velocity distribution in height direction of symmetrical rolling and snake rolling
4.2 Comparison of equivalent strain between symmetrical rolling and snake rolling
The comparison of equivalent strain distribution in height direction between symmetrical rolling and snake rolling is shown in Fig. 3. The equivalent strain distribution is symmetrical in symmetrical rolling and the maximum equivalent strain locates at the subsurface (about 1/8 thickness of the surface). As the metal flows slower on the surface because of the influence of the friction force from direct contact with work rolls, the equivalent strain is smaller than that of the subsurface. The equivalent strain distribution is inhomogeneous in snake rolling. The equivalent strain in the lower layer is larger than the upper layer and it is also larger than the same position in symmetrical rolling. However, the equivalent strain in the upper layer is smaller than the same position in symmetrical rolling. This phenomenon can be explained as follows: the metal flows more quickly due to larger velocity in the lower roll, which results in larger strain in the lower layer of the plate; when pass reduction is fixed, the strain in the upper layer becomes small correspondingly. The equivalent strain in the center point of the plate is 0.143 in symmetrical rolling and 0.146 in snake rolling. Compared with symmetrical rolling, it is 2.1% larger in the center point in snake rolling, indicating that snake rolling is beneficial to penetrate the strain into the central portion of plates in the height direction.
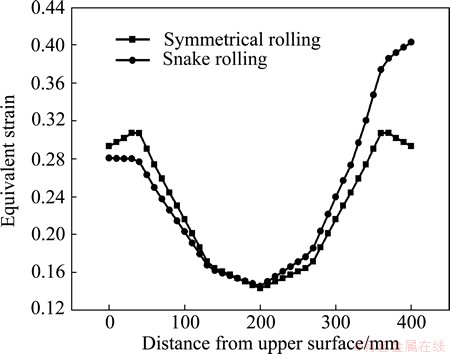
Fig. 3 Equivalent strain distribution in height direction of symmetrical rolling and snake rolling
4.3 Comparison of equivalent stress between symmetrical rolling and snake rolling
The comparison of equivalent stress distribution in height direction between symmetrical rolling and snake rolling is presented in Fig. 4. The stress distribution is symmetrical and is similar to the strain distribution, while the stress in the lower layer of the plate is larger than that in the upper layer in snake rolling. However, the stress in the center point is almost the same in symmetrical rolling and snake rolling. In snake rolling, larger velocity in the lower roll results in larger strain and shear stress in the lower layer of the plate. Therefore, the stress distribution is inhomogeneous in snake rolling.
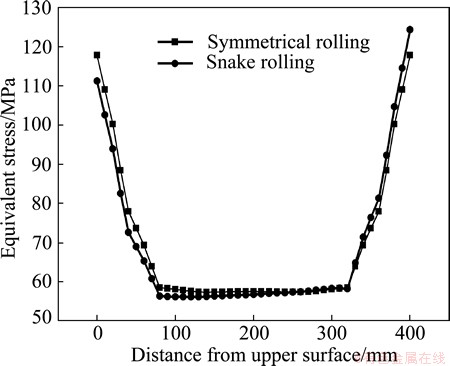
Fig. 4 Equivalent stress distribution in height direction of symmetrical rolling and snake rolling
4.4 Effect of velocity ratio on strain distribution
Figure 5 shows the effect of velocity ratio on the shear strain along the rolling direction in the center point of plate. It can be easily found that the shear strain in the center point is increased with the increase of velocity ratio and this phenomenon is consistent in different offset distances in Fig. 5. With the increase of velocity ratio, the area of the rub zone where friction force is in opposite direction in the surface is becoming larger in deformation zone. In rub zone, the shear stress applied to the plate is quite large. Therefore, a large rub zone will make a large shear strain in the center point of the plate. However, under the given offset distance, the curvature of the rolled plate is increased with the increase of velocity ratio and large curvature will seriously affect the following passes. A proper speed ratio should be selected to acquire large shear strain in the center portion of the plate and to ensure that the following passes can be conducted at the same time.
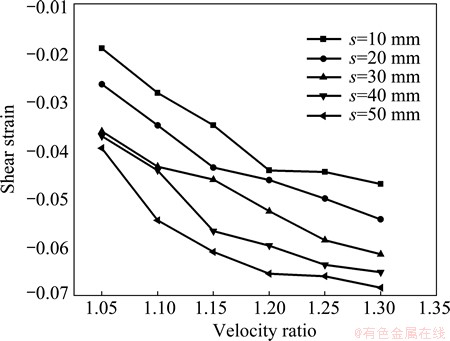
Fig. 5 Effect of velocity ratio on shear strain along rolling direction in center point
From the preceding section, the strain distribution is inhomogeneous and the strain in the lower layer is much larger. To study the effect of speed ratio on the inhomogeneity of the strain distribution in the height direction of rolled plate, a non-uniform coefficient α is defined as follows:
α=(ε2-ε1)/ε1×100%
where ε1 and ε2 represent the equivalent strains in the upper and lower surface, respectively. The effect of velocity ratio on the non-uniform coefficient of the strain distribution is shown in Fig. 6. From Fig. 6, it is obvious that the non-uniform coefficient is increased with the increase of velocity ratio at a given offset distance. As the velocity ratio increases, the strain in the lower layer increases quickly and the strain in the upper layer becomes smaller correspondingly, thus increasing the inhomogeneity of the strain distribution in the height direction of rolled plate.

Fig. 6 Effect of velocity ratio on non-uniformity of plate in height direction
4.5 Effect of offset distance on strain distribution
Figure 7 shows the effect of offset distance on the shear strain along the rolling direction in the center point of plate. The shear strain in the center point is increased with the increase of offset distance and this phenomenon is consistent in different velocities ratios in Fig. 7. In symmetrical rolling, neutral points of the upper and lower roll are in the same vertical line, so the rolling forces applied to the plate from two work rolls are also in the same vertical line. As a result, the rolled plate is mainly subjected to compressive deformation. However, two rolling forces will form a rolling moment because there is an offset distance in the rolling forces applied to the plate in snake rolling. For a given velocity ratio, as offset distance increases, the distance between two rolling forces increases and the rolling moment increases accordingly. As a consequence, in addition to compressive deformation, the plate is subjected to a strong shear strain, which contributes to large shear deformation in the center portion of the plate.

Fig. 7 Effect of offset distance on shear strain along rolling direction in center point
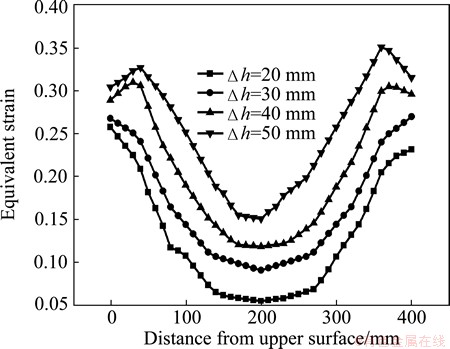
Fig. 8 Effect of pass reduction on equivalent strain distribution of symmetrical rolling
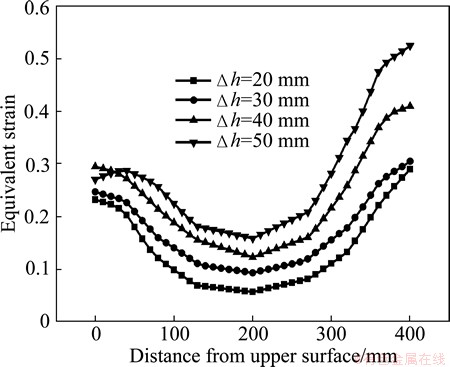
Fig. 9 Effect of pass reduction on equivalent strain distribution of snake rolling
4.6 Effect of pass reduction on strain distribution
Effects of pass reduction on equivalent strain distribution in height direction of symmetrical rolling and snake rolling are shown in Fig. 8 and Fig. 9 respectively. As can be seen, as pass reduction increases, the equivalent strain distribution is symmetrical and the strains on the surface and the center portion are both increased in symmetrical rolling. The strain increase in the lower layer is much larger than that in the upper layer in snake rolling, thus enlarging the inhomogeneity of the strain distribution in the height direction of rolled plate. In snake rolling, the strain in the lower layer is larger and the deformation can be quickly penetrated into the core portion because of larger velocity in the lower roll as pass reduction increases. While the strain is smaller in the upper layer and the deformation is difficult to penetrate into the center point. Therefore, the strain in all positions of the plate is increased as pass reduction increases in both symmetrical rolling and snake rolling. The strain increase in the lower layer is much larger than that in the upper layer in snake rolling. The equivalent strain in the center point of the plate is 0.1506 in symmetrical rolling and 0.1583 in snake rolling when pass reduction is 50 mm. Compared with symmetrical rolling, it is 5.1% larger in the center point in snake rolling, indicating that snake rolling is beneficial to penetrate the strain into the central portion of plates in the height direction with a larger pass reduction.
Effects of pass reduction on the shear strain along the rolling direction in the center point of plate in snake rolling are presented in Fig. 10. It can be easily found that the shear strain is increased with the increase of pass reduction and offset distance, which is in good agreement with the previous discussion in this article. When pass reduction increases, the depth of the strain which can be penetrated into is substantially increased. Besides, the center point is subjected to large shear stress, which generates large shear strain with the increase of pass reduction.

Fig. 10 Effect of pass reduction on shear strain along rolling direction in center point
5 Conclusions
1) The metal in the lower layer of the plate flows more quickly in snake rolling, which results in larger equivalent strain in the lower layer and inhomogeneous strain distribution in the height direction.
2) As velocity ratio increases, the equivalent strain in the lower layer increases more quickly and the strain in the upper layer becomes smaller correspondingly, thus increasing the inhomogeneity of the strain distribution in the height direction of rolled plate.
3) The shear strain along the rolling direction in the center point of thick plate is almost zero during symmetrical rolling, while it is much larger during snake rolling because of the existence of rub zone. Also, the shear strain in the center point is increased with the increase of velocity ratio and offset distance, which indicates that the deformation can be quickly penetrated into the core portion of the thick plate in snake rolling.
4) As pass reduction increases, the equivalent strain distribution is symmetrical and the strains of the surface and the center portion are both increased in symmetrical rolling. In snake rolling, the strain increase in the lower layer is much larger than that in the upper layer and the inhomogeneity of the strain distribution in the height direction is increased with the increase of pass reduction.
References
[1] LI Xing-dan. Development of commercial aircraft aluminum alloy structural materials [J]. Shanghai Nonferrous Metals, 1994, 15(3): 160-168. (in Chinese)
[2] WANG Zhu-tang. World aluminum foil rolling industry [M]. Changsha: Central South University Press, 2010: 40. (in Chinese)
[3] YANG Shi-de. Introduction of asymmetric aluminum hot rolling and mill [J]. World Nonferrous Metals, 2010(2): 47. (in Chinese)
[4] FU Yao. Study on snake rolling of aluminum alloy thick plate with high strength and high toughness [D]. Beijing: Beijing Nonferrous Metal Research Institute, 2011. (in Chinese)
[5] DING H, KANAMORI N, HONMA T. FEM analysis for hot rolling process of AM60 alloy [J]. Transactions of Nonferrous Metals Society of China, 2008, 18: s242-s246.
[6] HUANG Chang-qin, DIAO Jin-peng, DENG Hua, LI Bing-ji, HU Xing-hua. Microstructure evolution of 6016 aluminum alloy during compression at elevated temperatures by hot rolling emulation [J]. Transactions of Nonferrous Metals Society of China, 2013, 23(6): 1576-1582.
[7] GUAN Ren-guo, ZHAO Zhan-yong, CHAO Run-ze, ZHAO Hong-liang, LIU Chun-ming. Effects of technical parameters of continuous semisolid rolling on microstructure and mechanical properties of Mg-3Sn-1Mn alloy [J]. Transactions of Nonferrous Metals Society of China, 2013, 23(1): 73-79.
[8] MOVSAVI S, EBRAHIMI S M, MADOLIAT R. Three dimensional numerical analyses of asymmetric rolling [J]. Journal of Materials Processing Technology, 2007, 187: 725-729.
[9] ZUO Fang-qing, JIANG Jian-hua, SHAN Ai-dang, FANG Jian-min, ZHANG Xing-yao. Shear deformation and grain refinement in pure Al by asymmetric rolling [J]. Transactions of Nonferrous Metals Society of China, 2008, 18(4): 774-777.
[10] YUAN Fu-shun, SUN Ji-quan. Deformation analysis in deformation zone of asymmetrical rolling with different roll velocity [J]. Shandong Metallurgy, 2010, 32(6): 25-27. (in Chinese)
[11] LIU Jie, KAWALLA R. Influence of asymmetric hot rolling on microstructure and rolling force with austenitic steel [J]. Transactions of Nonferrous Metals Society of China, 2012, 22(S2): s504-s511.
[12] LEE K, LEE H. Grain refinement and mechanical properties of asymmetrically rolled low carbon steel [J]. Journal of Materials Processing Technology, 2010, 210(12): 1574-1579.
[13] WANG Hai-lu, WANG Guo-jun, HU Lian-xi, WANG Qiang, WANG Er-de. Effect of hot rolling on grain refining and mechanical properties of AZ40 magnesium alloy [J]. Transactions of Nonferrous Metals Society of China, 2011, 21(S2): s229-s234.
[14] CUI Q, OHORI K. Grain refinement of high purity aluminium by asymmetric rolling [J]. Materials Science and Technology, 2000, 16(10): 1095-1101.
[15] JIN H, LLOYD D J. Evolution of texture in AA6111 aluminum alloy after asymmetric rolling with various velocity ratios between top and bottom rolls [J]. Materials Science and Engineering A, 2007, 465(1): 267-273.
[16] SUZUKI Y, NOGUCHI O, MIKI Y, UENO Y, KOYAMA K, KOMATSUBARA T. Evolution of recrystallization texture in aluminum alloy sheets by asymmetric-warm-rolling [J]. Furukawa- Sky Review, 2012, 8: 37-41.
[17] SALIMI M, SASSANI F. Modified slab analysis of asymmetrical plate rolling [J]. International Journal of Mechanical Sciences, 2002, 44(9): 1999-2023.
[18] SALIMI M, KADKHODAEI M. Slab analysis of asymmetrical sheet rolling [J]. Journal of Materials Processing Technology, 2004, 150(3): 215-222.
[19] FARHAT-NIA F, SALIMI M, MOVAHHEDY M R. Elasto-plastic finite element simulation of asymmetrical plate rolling using an ALE approach [J]. Journal of Materials Processing Technology, 2006, 177(1): 525-529.
[20] QWAMIZADEH M, KADKHODAEI M, SALIMI M. Asymmetrical sheet rolling analysis and evaluation of developed curvature [J]. The International Journal of Advanced Manufacturing Technology, 2012, 61(1-4): 227-235.
[21] GUDUR P P, SALUNKHE M A, DIXIT U S. A theoretical study on the application of asymmetric rolling for the estimation of friction [J]. International Journal of Mechanical Sciences, 2008, 50(2): 315-327.
[22] BYON Sang-Min, NA Doo-Hyun, LEE Young-Seog. Flow stress equation in range of intermediate strain rates and high temperatures to predict roll force in four-pass continuous rod rolling [J]. Transactions of Nonferrous Metals Society of China, 2013, 23(3): 742-748.
[23] FU Yao, XIE Shui-sheng, XIONG Bo-qing, HUANG Guo-jie, CHENG Lei. Calculation of rolling force in snake rolling by slab method [J]. Journal of Plasticity Engineering, 2010, 17(6): 103-109. (in Chinese)
[24] FU Yao, XIE Shui-sheng, XIONG Bo-qing, HUANG Guo-jie, CHENG Lei, XIAO Xiang-peng. Study on curvature analytical model of aluminum alloy thick plate in snake rolling [J]. Chinese Journal of Rare Metals, 2011, 35(6): 805-811. (in Chinese)
[25] QUAN Guo-zheng, ZHANG Yan-wei, WANG Feng-biao, ZHOU Yi-jun, ZHOU Jie. Dynamic recrystallization kinetics model of 7075 aluminum alloy during thermoplastic deformation [J]. Materials for Mechanical Engineering, 2011, 35(12): 97-101. (in Chinese).
张 涛1,2,吴运新1,2,龚 海1,2,郑细昭1,2,蒋绍松1,2
1. 中南大学 机电工程学院,长沙 410083;
2. 中南大学 高性能复杂制造国家重点实验室,长沙 410083
摘 要:介绍了蛇形轧制的实现方式。运用数值模拟方法,在Deform 3D上分析单道次轧制过程中蛇形轧制和对称轧制7075铝合金厚板的流动速度及应力应变分布情况,分析异速比、上下轧辊错位量和压下量对蛇形轧制变形区内轧板等效应变和剪切应变的影响规律。结果表明:蛇形轧制中,由于下辊速度快,轧板下层金属流动比上层快,蛇形轧制中轧板下层等效变形大于上层,且随着异速比的增大,上下层金属变形差距增大;对称轧制中厚板心部的剪切应变几乎为0,蛇形轧制中由于有“搓轧区”的存在,厚板心部的剪切应变远大于对称轧制的,且随着异速比的增加和错位量的增加,轧板心部的剪切变形增大。这种附加的剪切变形有利于使变形向厚板心部渗透,从而改善厚板高向变形的不均匀性。
关键词:有限元仿真;7075铝合金;蛇形轧制;剪切变形;异速比;错位量;压下量
(Edited by Xiang-qun LI)
Foundation item: Projects (2012CB619505, 2010CB731703) supported by the National Basic Research Program of China; Project (CX2013B065) supported by Hunan Provincial Innovation Foundation for Postgraduate, China; Project (117308) supported by Postdoctoral Science Foundation of Central South University, China
Corresponding author: Yun-xin WU; Tel: +86-731-88877840; E-mail: wuyunxin@csu.edu.cn
DOI: 10.1016/S1003-6326(14)63326-4

