DOI: 10.11817/j.issn.1672-7207.2015.11.015
光伏系统中全局最大功率点的优化
张贵涛1,夏向阳1,王锦泷1,赵思然2
(1. 长沙理工大学 电气与信息工程学院,湖南 长沙,410114;
2. 广东工业大学 应用数学学院,广东 广州,510520)
摘要:针对当光伏列阵接收到不均匀光照时,整个光伏系统的P-V曲线变为多峰值曲线,采用传统的最大功率点跟踪方法不能很好地追踪最大功率点的问题,提出一种基于改进的模拟退火-粒子群算法的最大功率点跟踪方法。研究结果表明:该优化算法中加入存储单元,保证了算法不会陷入局部最大值点,同时引入粒子群适值函数,调整退火温度,保证了运行速度;通过该方法可以快速的准确地找到光伏系统的全局最大功率点;仿真结果证明了该算法的正确性。
关键词:光伏发电系统;多峰值;模拟退火-粒子群算法;全局MPPT
中图分类号:TM615 文献标志码:A 文章编号:1672-7207(2015)11-4077-06
Global MPPT optimal control method of PV system
ZHANG Guitao1, XIA Xiangyang1, WANG Jinlong1, ZHAO Siran2
(1. College of Electrical and Information Engineering, Changsha University of Science & Technology,
Changsha 410114, China;
2. School of Applied Mathematics, Guangdong University of Technology, Guangzhou 510520, China)
Abstract: Considering that when the photovoltaic (PV) array receives the partially shaded condition (PSC), P-V curve of the entire PV system becomes multi-peak curve, and that using the traditional maximum power point tracking methods cannot achieve the maximum power point tracking well, a global maximum power point tracking (MPPT) control method based on particle swam optimization-simulated annealing (PSO-SA) was put forward. The results show that the optimization algorithm does not fall into the local maximum points when the storage unit is added, that the operation speed can be ensured when the particle swarm fitness function is introduced, and that the annealing temperature is adjusted. By this method, the global maximum power point of PV systems can be located quickly and accurately. The simulation results verify the correctness of the algorithm.
Key words: photovoltaic system; multi-peak condition; particle swam optimization-simulated annealing (PSO-SA); global MPPT
太阳能作为清洁能源中的重要组成部分,近年来被人们熟知并加以利用。光伏发电技术在人们开发和使用太阳能的过程中变得越来越完善。光伏发电是由一些特殊的半导体材料经过光伏效应将太阳能转换为电能而供给人们使用。为了提高太阳能的利用率,越来越多的先进技术被应用到光伏发电中。最大功率点追踪技术(MPPT)作为其中的关键技术也越来越受到研究者的重视。光伏列阵周围的建筑和数目以及光伏板上的灰尘等会造成光伏列阵的局部阴影,在这种情况下,光伏列阵的输出特性就会发生不规则变化,输出功率会出现多个局部最大值点,采用传统的方法如爬山法、扰动观察法、电导增量法等无法对局部最大值点和全局最大值点进行区分。局部阴影情况下光伏列阵的输出特性为本文研究提供了重要依据[1-3]。肖景良等[4]提出了一种通过优化光伏列阵分布格局的方法来实现对最大功率点的追踪。这种方法的局限性很强,并且需要对光照和温度进行准确预测。肖晓霞等[5-6]提出了一种对输出功率进行实时检测,并且不断更新最大功率点所对应的端电压,但需采集大量信息和计算。李天博等[7-9]提出了一种基于粒子群算法的最大功率点追踪。该算法可以通过适值函数、约束条件和终止函数对全局最大功率点进行准确定位。但普通的粒子群算法为了找到目标点要进行多次迭代,造成输出功率和端电压的震荡影响输出,并且定位越准确,所需时间就越长,对电路的稳定性影响就越大。为此,本文作者提出一种局部阴影情况下追踪光伏列阵的全局最大功率点改进的模拟退火-粒子群算法。该方法对传统的粒子群算法进行优化,使其速度更快,目的性更强,在能准确定位目标点的同时,提高算法的速度和系统的稳定性。
1 太阳能电池数学模型分析
太阳能电池模块采用的是半导体材料,与传统的半导体材料不同的是经光照后可以产生电动势即光伏效应。为了描述电池的工作状态,往往将电池及负载系统统一用等效电路来模拟。理想的光伏电池可以看作电流源及二极管[10]。太阳能电池等效电路图见图1。
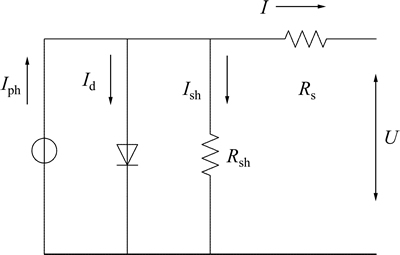
图1 太阳能电池等效电路图
Fig. 1 Diagram of solar battery equivalent circuit
图1中:I为太阳能电池输出电流;Iph为光生电流;Id为流过等效二极管的电流;V为光伏电池端电压;Rs为太阳能电池的串联电阻;Rsh为内部漏损电阻;Ish为流过内部漏损电阻Rsh的电流。由于该等效模型考虑了太阳能电池的所有电阻,因此,可以更实际地代替太阳能电池的物理模型。分析图1可得
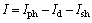 (1)
(1)
其中:
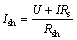 (2)
(2)
通过二极管的电流Id与正向偏压Ud分别为:
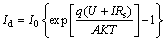 (3)
(3)
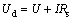 (4)
(4)
 (5)
(5)
一般来说,R0很小,Rsh很大,故式(5)可以简化为
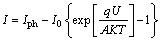 (6)
(6)
式中:A为二极管特性因子(一般为1.5);K为波尔兹曼常数;T为太阳能电池工作时的热力学温度;q为电子电荷量;U为光伏电池端电压。
在不同温度下,光伏板的I-V特性曲线和P-V特性曲线分别如图2和图3所示。输出功率曲线呈现单峰值的特性,光伏板输出功率只有1个最大值[11]。
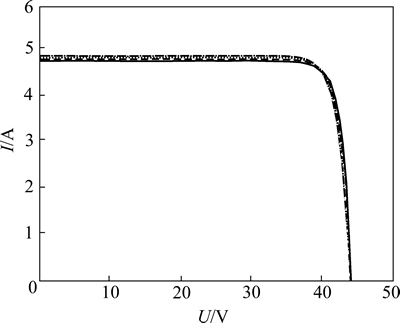
图2 不同温度下的I-V特性曲线
Fig. 2 I-V curve under different temperatures
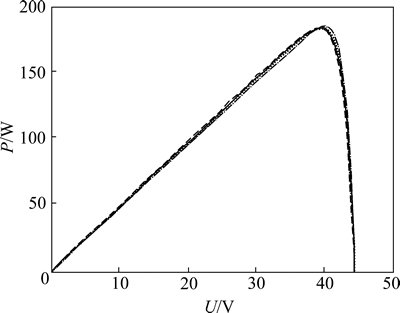
图3 不同温度下的P-V特性曲线
Fig. 3 P-V curve under different temperatures
2 局部遮阴情况下光伏板输出特性
光伏列阵是由多个光伏模块串并联形成的,见图4。如图4所示,将太阳能电池组件进行串并联组装成方阵。串联时,需要工作电流相同的组件,并为每个组件并接旁路二极管;并联时,需要工作电压相同的组件。

图4 光伏列阵结构
Fig. 4 Structure of photovoltaic array
当光伏列阵处于局部阴影情况时,各个光伏模块接收到的光强不同,光伏模块的 曲线发生了改变,因而,整个光伏列阵的
曲线发生了改变,因而,整个光伏列阵的 曲线也发生了改变[12-13]。遮阴情况下的电流曲线和功率曲线分别见图5和图6。
曲线也发生了改变[12-13]。遮阴情况下的电流曲线和功率曲线分别见图5和图6。
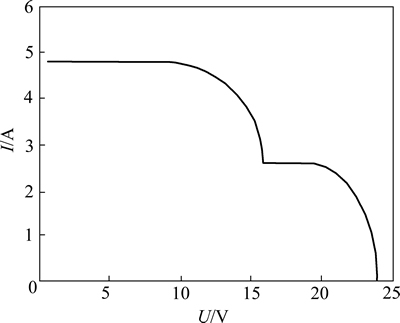
图5 局部阴影情况下的电流曲线
Fig. 5 Current curve under partially shaded condition
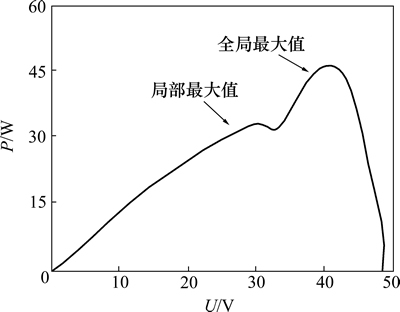
图6 局部阴影情况下的功率曲线
Fig. 6 Power curve under partially shaded condition
分析图5和图6可知:当光伏板部分遮阴时,输出功率曲线会呈现多峰值的特性,所有的峰值点中只有1个为全局最大功率点,其他的峰值点为局部最大功率点。传统的MPPT算法在这种情况下并不能很好地追踪到最大功率点,为此,本文作者提出一种改进的模拟退火-粒子群算法,对局部阴影情况下光伏列阵的全局最大功率点进行追踪。
3 改进的模拟退火-粒子群算法
PSO是基于群集智能的以寻求全局最优解为目的的一种优化工具,粒子通过不停地更新自己的速度来向最优解方向“飞行”[14-15]。作为1个多维向量,粒子的飞行速度根据自身的记忆以及社会共享信息来决定。当惯性系数较大时,粒子可能飞过最优解的区域,从而错失对全局最优解的搜索;而当惯性系数较小时,会影响收敛到最优解的时间。可见,合理的惯性系数决定了粒子能否快速准确的找到最优解。本文采用一种自适应惯性系数:
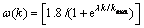 (7)
(7)
式中: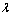 为正系数;k为迭代数;kmax为迭代数上限。通过可变的惯性系数来保证能够快速、准确地找到最优解。
为正系数;k为迭代数;kmax为迭代数上限。通过可变的惯性系数来保证能够快速、准确地找到最优解。
在此算法的每个并行过程中,加入模拟退火机制来提高算法的速度,同时在求解过程中加入存储器,记录当前过程中出现的最优解,在此过程结束后对存储器中的数值进行比较,得到最优解,得出的结果跳出了局部最大值。
4 基于PSO-SI多峰值MPPT的算法设计
本文提出的是在局部阴影情况下的MPPT算法,因而目标函数应为全局功率,变量为光伏板的输出电压。在使用PSO优化时,粒子的位置应定义为阵列电压,在粒子进行迭代的同时计算适值函数值,以调整退火温度,提高计算速度。
4.1 适值函数的确立
通过调用1个适应度函数判断每个粒子对目标函数的适应度;通过对适应度进行分析,寻找输出功率最大点所对应的光伏板输出电压,得到全局最优解。粒子对于目标的适应度函数f为:
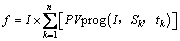 (8)
(8)
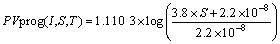 (9)
(9)
式中:f为微粒子的适应度函数;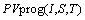 为太阳能模块的输出特性函数,给定温度为25°;S为光照强度;t为温度。计算和比较每个粒子的适应值,对粒子速度进行更新。式(8)为单个模块的电压电流公式,通过计算得到输出功率。
为太阳能模块的输出特性函数,给定温度为25°;S为光照强度;t为温度。计算和比较每个粒子的适应值,对粒子速度进行更新。式(8)为单个模块的电压电流公式,通过计算得到输出功率。
4.2 粒子速度更新
在迭代过程中,粒子通过自身记忆和群体共享信息更新自己的速度向量,根据式(8)和式(9)进行计算。
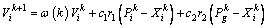 (10)
(10)
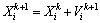 (11)
(11)
式中:
 (12)
(12)
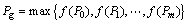 (13)
(13)
式中:m为粒子数目;c1和c2为根据经验设定的随机常数;f为目标函数;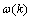 为自适应惯性系数;Pi为个体最佳位置;Pg为群体信息提供的最佳位置。
为自适应惯性系数;Pi为个体最佳位置;Pg为群体信息提供的最佳位置。
4.3 算法终止策略
在反复迭代过程中,系统会产生趋于稳态时的功率震荡。当所有的粒子位置和飞行速度都向1个方位收敛时,可认为已经达到目标位置附近。为了减小功率长时间波动,尽快到达收敛区间,本文提出的终止策略如下:当粒子之间的最大电压差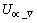 小于阵列开路电压
小于阵列开路电压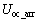 的0.5%时停止迭代,当前的功率定义为最大功率点Pmi。将每个极大值功率点存储到存储器中,经比较得出最大值点Pm。
的0.5%时停止迭代,当前的功率定义为最大功率点Pmi。将每个极大值功率点存储到存储器中,经比较得出最大值点Pm。
4.4 多峰值MPPT具体操作流程
经过上述分析得到新型控制算法在遮阴情况下MPPT中的使用流程如图7所示。
加入了模拟退火的粒子群算法运算过程如下。
1) 初始化粒子群。通过经验和实验数据[9],确定粒子初速度以及初始位置(初始电压)。
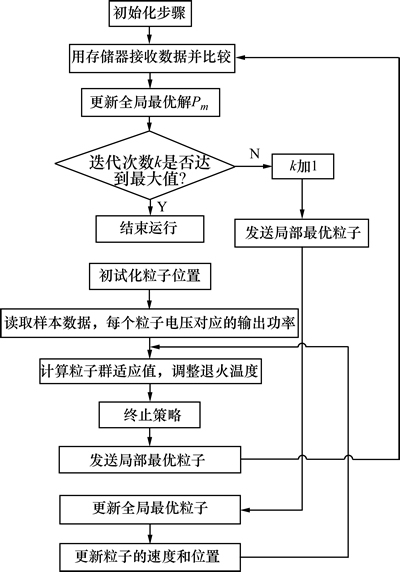
图7 新型算法流程图
Fig. 7 Flow chart of new algorithm
2) 通过式(8)和式(9)确定粒子的适应度。
3) 计算适应值,调整退火温度[1]。
4) 将粒子自身的记忆和群体信息进行比较,更新自己的速度向量。
5) 在更新速度向量时,引入前面提出的自适应惯性系数。
6) 将粒子达到终止策略时的位置计入存储器,比较每点处功率。
7) 结束运行,等待重置。
5 仿真和分析
为了检测新型模拟退火粒子群算法在MPPT中的运用,采取对比方式进行研究。光伏列阵运用多个光伏模块来实现,将光伏模块的光照强度变为1 000 W/m2和600 W/m2模拟遮阴情况。基于BOOST电路的最大功率出跟踪系统见图8。
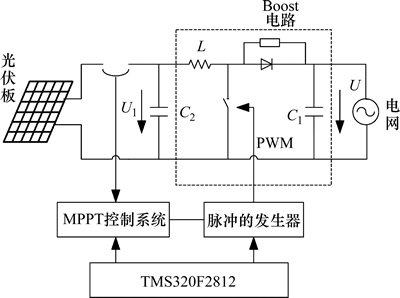
图8 基于BOOST电路的最大功率出跟踪系统
Fig. 8 BOOST-based MPPT system
光伏列阵输出电压U1为BOOST电路输入电压,BOOST电路输出电压U被钳制在电网电压上保持不变。MPPT控制系统通过运用模拟退火-粒子群算法进行计算。运用式(9)获得最大功率输出时对应的电压,通过BOOST电路改变电压U1。更新光伏列阵电压,脉冲发生器产生PWM波来改变开关占空比,从而实现对最大功率点的跟踪。仿真参数如下:升压电感L为0.15 mH;母线侧电容C1为5.00 mF;滤波电容C2为1.00 mF。该算法中粒子初始位置根据经验确定。根据图6确定粒子初始位置,也就是电压初始的取值:U1,U2和U3分别为25,35和45 V。
分别在无遮阴情况和有遮阴情况下,运用模拟退火-粒子群算法以及传统的扰动观察法进行仿真,对所得到的结果进行对比。经过仿真,所得不同条件下的最大功率如表1所示。
表1 不同条件下的最大功率
Table 1 Maximum power of different conditions
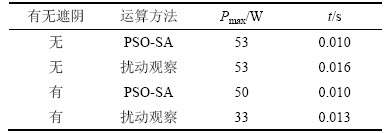
从表1可以看出:运用模拟退火-粒子群算法(PSO-SI)对光伏板进行跟踪可以准确、迅速地找到目标点,并且实施跟踪。
图9和图10所示分别为遮阴情况下不同算法的光伏板功率输出曲线。
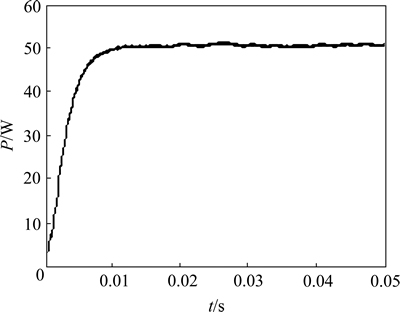
图9 遮阴时新型算法下的输出功率
Fig. 9 Output power with new method under shaded condition
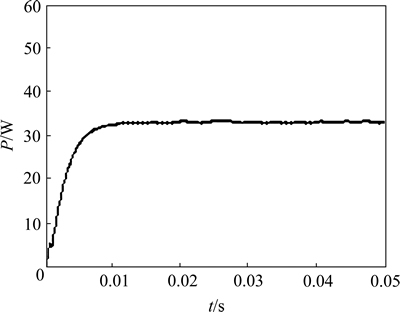
图10 遮阴时扰动观察法下的功率曲线
Fig. 10 Power curve with perturbation and observation control method under shaded condition
从图 9可以看出:采用新型算法时,最大功率在50 W左右波动,在0.01 s时攀升至最大功率输出。从图10可以看出:采用扰动观察法时,在0.013 s时攀升至最大功率输出,也就是在第1个极值点,但输出只有33 W左右。而实际情况中光伏列阵的全局最大功率点不一定在第1个极值点,因而,采用本文提出的算法更符合实际。
6 结论
1) 本文优化了模拟退火-粒子群算法,在传统的方法中引入存储单元来避免算法陷入局部最优,引入了自适应惯性系数来控制粒子的飞行速度,引入适值函数来调整退火温度。
2) 将该算法运用到光伏系统遮阴情况下的全局最大功率点跟踪中,仿真结果验证了该方法的可行性。采用该方法可以快速、准确地对光伏列阵的全局最大功率点进行追踪。
参考文献:
[1] 夏向阳, 龚芬, 曾小勇, 等. 优化配置配电网的谐波抑制装置研究[J]. 电工电能新技术, 2011, 30(3): 84-88.
XIA Xiangyang, GONG Fen, ZENG Xiaoyong, et al. Distribution network optimization of filter suppression device[J]. Adv Tech of Elec Eng & Energy, 2011, 30(3): 84-88.
[2] 刘晓艳, 祁新梅, 郑寿森, 等. 局部阴影条件下光伏阵列的建模与分析[J]. 电网技术, 2010, 34(11): 192-197.
LIU Xiaoyan, QI Xinmei, ZHENG Shousen, et al. Model and analysis of photovoltaic array under partial shading[J]. Power System Technology, 2010, 34(11): 192-197.
[3] 夏向阳, 周云, 帅志康. 高压直流输电系统中模块化多电平换流器的重复预测控制[J]. 中国电机工程学报, 2015, 35(7): 1637-1643.
XIA Xiangyang, ZHOU Yu, SHUAI Zhikang. Repeat predictive control of modular multilevel converter in high voltage direct current system[J]. Proceedings of the CSEE, 2015, 35(7): 1637-1643.
[4] 肖景良, 徐政, 林崇, 等. 局部阴影条件下光伏阵列的优化设计[J]. 中国电机工程学报, 2009, 29(11): 119-124.
XIAO Jingliang, XU Zheng, LIN Chong, et al. Optimal design of photovoltaic arrays under partial shading[J]. Proceedings of the CSEE, 2009, 29(11): 119-124.
[5] 肖朝霞, 刘东, 赵倩宇. 多功能光伏发电系统仿真设计[J]. 电力科学与技术学报, 2012, 3(4): 12-16.
XIAO Zhaoxia, LIU Dong, ZHAO Qianyu, et al. Multifunction photovoltaic system design simulation[J]. Electric Power Science and Technology, 2012, 3(4): 12-16.
[6] 胡浩磊, 杨富文. 部分遮阴条件下光伏阵列最大功率点跟踪方法[J]. 电源学报, 2013, 2(4): 23-29.
HU Haolei, YANG Fuwen. Maximum power point tracking method for PV array under partially shaded conditions[J]. Journal of Power Supply, 2013, 2(4): 23-29.
[7] 李天博, 褚俊, 陈坤华. 基于粒子群算法的 MPPT仿真及应用[J]. 电力电子技术, 2012, 46(1): 7-9.
LI Tianbo, ZHU Jun, CHEN Kunhua. The maximum power point tracking simulation and application based on particle swarm optimization[J]. Power Electronics, 2012, 46(1): 7-9.
[8] 刘艳莉, 周航, 程泽. 基于粒子群优化的光伏系 MPPT 控制方法[J]. 计算机工程, 2010, 36(15): 265-267.
LIU Yanli, ZHOU Hang, CHENG Ze. MPPT control method of PV system based on PSO[J]. Computer Engineering, 2010, 36(15): 265-267.
[9] 刘晓丹. 基于粒子群算法的光伏系统最大功率点跟踪研究[D]. 南京: 南京邮电大学自动化学院, 2013: 25-30.
LIU Xiaodan. Maximum power point tracking photovoltaic system based on particle swarm optimization[D]. Nanjing: Nanjing University of Posts and Telecommunications. College of Automation, 2013: 25-30.
[10] 崔荣强, 春江, 吴达成. 并网型太阳能光伏发电系统[M]. 北京: 化学工业出版社, 2007: 30-42.
CUI Rongqiang, CHUN Jiang, WU Dacheng. Riverside and grid solar photovoltaic systems[M]. Beijing: Chemical Industry Press, 2007: 30-42.
[11] 刘方锐, 康勇, 张宇. 光伏并网逆变器的孤岛检测技术[J]. 电力科学与技术学报, 2009, 24(1): 8-12.
LIU Fangrui, KANG Yong, ZHANG Yu, et al. Islanding detection technology and the photovoltaic inverter[J]. Electric Power Science and Technology, 2009, 24(1): 8-12.
[12] 陈阿莲, 冯丽娜, 杜春水, 等. 基于支持向量机的局部阴影条件下光伏阵列建[J]. 电工技术学报, 2011, 26(3): 140-146.
CHEN Alian, FENG Lina, DU Chunshui, et al. Modeling of photovoltaic array based on support vector machines under partial shaded conditions[J]. Transactions of China Electrotechnical Society, 2011, 26(3): 140-146.
[13] Ishaque K, Salam Z, Taheri H, et al. Maximum power point tracking for PV system under partial shading condition via particle swarm optimization[C]// Applied Power Electronics Colloquium (IAPEC). Johor Bahru, Malaysia: IEEE, 2011: 5-9.
[14] 史文华. 光伏系统最大功率点跟踪控制方法研究[D]. 保定: 华北大学电子与信息工程学院, 2012: 1-30.
SHI Wenhua. Research photovoltaic system MPPT control[D]. Baoding: North China University. School of Electrical & Electronic Engineering, 2012: 1-30.
[15] Patel H, Agarwal V. Maximum power point tracking scheme for PV systems opera ting under partially shaded conditions[J]. IEEE Transactions on Industrial Electronics, 2008, 55(4): 1689-1698.
(编辑 陈灿华)
收稿日期:2014-11-12;修回日期:2015-01-16
基金项目(Foundation item):湖南省自然科学基金资助项目(2011JJ5027);长沙市科技计划项目(K1501012-11) (Project(2011JJ5027) supported by the Natural Science Foundation of Hunan Province; Project(K1501012-11) supported by the Changsha Science and Technology)
通信作者:夏向阳,博士(后),教授,硕士生导师,从事电力电子技术在电力系统的应用研究;E-mail: xia_xy@126.com