J. Cent. South Univ. (2020) 27: 566-577

DOI: https://doi.org/10.1007/s11771-020-4317-y

Controlling deflection of long steel I-shaped girder bridge using two V-shaped pre-tensioning cables

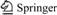
Fatemeh PARTOVI, Nader FANAIE

Department of Civil Engineering, K. N. Toosi University of Technology, Tehran, Iran

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020

Abstract: Despite appropriate design of girder under bending and shear, the deflection of long steel girders usually exceeds the allowable range, and therefore the structural designers encounter challenges in this regard. Considering significant features of the cables, namely, low weight, small cross section, and high tensile strength, they are used in this research so as to control the deflection of long girder bridges, rather than increasing their heights. In this study, theoretical relations are developed to calculate the increase in pre-tensioning force of V-shaped steel cables under external loading as well as the deflection of steel girder bridges with V-shaped cables and different support conditions. To verify the theoretical relations, the steel girder bridge is modeled in the finite element ABAQUS software with different support conditions without cable and with V-shaped cables. The obtained results show that the theoretical relations can appropriately predict the deflection of girder bridge with V-shaped cables and different support conditions. In this study, the effects of the distance from support on the deflection of mid span are studied in both simply supported and fixed supported girder bridge so as to obtain the appropriate distance from support causing the minimum deflection.

Key words: deflection; steel bridge; I-shaped girder; V-shaped cable; pre-tensioning; least work

Cite this article as: Fatemeh PARTOVI, Nader FANAIE. Controlling deflection of long steel I-shaped girder bridge using two V-shaped pre-tensioning cables [J]. Journal of Central South University, 2020, 27(2): 566-577. DOI: https://doi.org/10.1007/s11771-020-4317-y.

1 Introduction

Reckoned as important components of a structure, cables are materials which can tolerate tensile force, and generally increase the stiffness and bearing capacity of a structure [1]. Nowadays, cables are increasingly used in structures. HOU et al [2] applied cable-cylinder bracing in the seismic retrofitting of steel flexural frames. From their view point, through this retrofitting method, the lateral strength of the storey augments without decreasing the ductility of flexural frame. FANAIE et al [3] presented theoretical relations for the cable- cylinder bracing system using a rigid cylinder like steel cylinder. They verified the results by finite element ABAQUS software. They also studied seismic behavior of steel flexural frames strengthened with cable-cylinder bracing and obtained reasonable results [4]. GIACCU [5] investigated the non-linear dynamic behavior of pre-tensioned-cable cross-braced structures in the presence of slackening in the braces. They concluded that there is a direct correlation between equivalent frequency and slackening in the braces. Pre-tensioning of steel beams through high strength cables is one of the most efficient methods so as to decrease the required steel and increase their bearing capacity. The pre-tensioning technique was primarily used in reinforced concrete structures; however, for the first time, it was utilized by DISCHINGER and MAGNEL in steel beams. Pre- tensioned steel structures are constructed all over the world, especially in America, Russia, and Germany. This fact shows the structural and economic merits of pre-stressed steel beams compared to non-prestressed ones. The pre-tensioning technique is appropriate to construct new structures as well as strengthening the existing ones [6].

Some researchers have studied pre-stressed composite beams using steel cable. AYYUB et al [7, 8] assessed pre-stressed steel-concrete composite beams experimentally as well as analytically using steel cable in the regions of positive and negative bending moments. They concluded that pre-tensioning increases the ultimate strength. NIE et al [9] presented theoretical relations to calculate the deflection as well as yield and ultimate moments of simply supported pre-stressed steel-concrete composite beam considering the slip effect. They verified the suggested formulas with the experimental results. ZHOU et al [10] presented the experimental study as well as numerical model of prestressed composite beams subjected to fire and positive moment. They observed that the fire resistance of composite beams prestressed with external tendons was highly influenced by the stress in the cable strands. Pre-stressed steel beams equipped with steel cables have been investigated by some researchers. TROITSKY [6] evaluated the behavior of pre-stressed steel beam using cables, and observed the increase in the stiffness and decrease in the deformation of the beam. BELLETTI et al [11] studied the behavior of pre-stressed simply supported steel I-shaped beams by tendons with focusing on two parameters, namely, the number of deviators and the value of prestressing force. PARK et al [12] analytically and experimentally evaluated the flexural behavior of steel I-beam pre-stressed with externally unbonded tendons. They figured out considerable increase in the yielding and ultimate bearing capacity of steel I-beam. KAMBAL et al [13] derived a finite-element formulation to investigate the effectiveness of applying the prestressing technique with respect to the flexural behavior of a simply supported steel box girder and they verified it by experimental results. ZHANG [14] examined the analytical solutions of the symmetric and antisymmetric elastic lateral- torsional buckling (LTB) of prestressed steel I-beams, with rectilinear tendons, under equal end moments and verified the correctness of the

analytical solutions by those simulated by using ANSYS. A number of researchers have investigated the dynamic behavior of pre-tensioned. NOBLE et al [15] studied the results of dynamic impact testing on externally axially loaded steel rectangular hollow sections (RHSs) and compared the response to that of externally post-tensioned steel RHSs. As well as, they tested the validity of the “compression-softening” effect for post-tensioned sections. They concluded that the “compression- softening” theory is not valid for pre- or post- tensioned sections. CAO et al [16] investigated the vibration performance of the arch prestressed concrete truss (APT) girder subjected to the on-site heel-drop and jumping impact tests and performed theoretical analyses. They concluded the theoretical fundamental natural frequency is in general agreement with the experimental result. MIYAMOTO et al [17] have studied the dynamic behavior of the pre-tensioned simply supported composite beam with external tendon. They derived the natural frequency equation of pre-tensioned beam based on the flexural vibration equation and verified the predicted equation by comparing it with the results of the dynamic experiment. PARK et al [18] analytically and experimentally studied the strengthening effect of bridges using external pre-tensioned tendons and concluded that strengthening reduces the mid span deflection by 10%-24%. REN et al [19] proposed the empirical formulas to estimate cable tension based on the solutions using energy method and fitting the exact solutions of cable vibration equations. They considered the cable sag and bending stiffness and verified the proposed formulas by the experimental results. Despite appropriate design of girders under bending and shear, their deflection usually exceeds the allowable range. In this research, the V-shaped steel cables are used so as to control the deflection of steel I-shaped girder bridges with various support conditions, rather than increasing their heights. The increase of pre-tensioning force of V-shaped steel cables subjected to external loading is determined by method of least work. Then, the method of virtual work is applied to developing the deflection relations of steel girder equipped with cables. In order to validate the obtained deflection relations, the results of theoretical relations are compared with those of finite element model of the girders.

2 Pre-tensioning symmetric I-shaped steel girder bridges with V-shaped steel cables

Symmetric I-shaped steel girder bridges have been intended with different support conditions, based on two different types, simply supported and fixed supported girder. As shown in Figure 1, pre-stressed V-shaped cables have been used in both sides of girder web, and subjected to external loading. As observed in the figure, the cable is fixed at both ends to the top flange of the girder in both sides of the web, and then, it passes through the deviators on the bottom flange causing the pattern with two inclined cables.

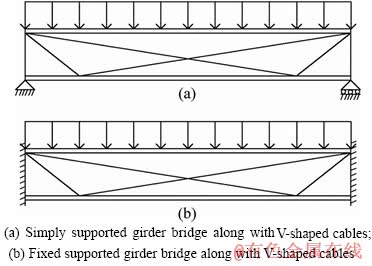
Figure 1 Pre-stressed symmetric I-shaped steel girder bridges with two V-shaped steel cable under external loading:

The following assumptions are taken into account to analyze pre-stressed symmetric I-shaped steel girders with steel cable:

1) The materials of steel girder and cable are linearly elastic;

2) The deformations are small;

3) Shear deformation is not considered;

4) The friction loss in the region of cable deformation and the relaxation of steel cable are ignored;

5) Steel girder section is rolled; therefore, it is compact.

3 Increase of pre-tensioning force of V-shaped steel cable in a girder bridge under external loading

The cable length increased by △L, and its pre-tensioning force, F_pt, increased by △F, under uniform distributed loading. The static equilibrium equations are not sufficient to calculate △F, because the structure is statically indeterminate. So, the increase of the force in the cable can be calculated using the method of least work.

To calculate the increase in pre-tensioning force of each cable through the method of least work, the total strain energy of the girder caused by its bending moment and axial force in different support conditions as well as the strain energy of each cable owing to its axial force are determined. Then, the relation of total strain energy is differentiated with respect to △F and the result is equated to zero to obtain the relation to increase the pre-tensioning force of the cable (△F).

3.1 Calculating increase in pre-tensioning force of V-shaped steel cables in simply supported girder bridge along with cables

Concerning the simply supported girder with the V-shaped cables, as shown in Figure 2, the horizontal component of the force of first inclined cable from the left side (C₁) should be equal to the horizontal component of the force of second inclined cable from the left side (C₂) to keep the bending moment continuous in the slope change region of cable. Therefore, if the increase in pre-tensioning force of steel cable is assumed as △F in the first slope part (C₁), then it will be equal to in the second slope part (C₂); hence, the axial force of the girder is equal to 2△Fcosθ₁.

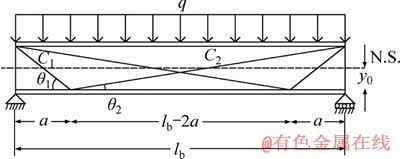
Figure 2 Simply supported girder bridge along with two V-shaped steel cables (N.S.-Neutral surface)

Considering the symmetry of structure and loading (Figure 2), the bending moment diagram plotted for right half of the girder is exactly the same as that of its left one. Therefore, the strain energy caused by bending moment can be determined for half of the girder and duplicated to calculate the bending strain energy for the whole girder. In what follows, bending moment is obtained for simply supported girder along with V-shaped steel cables under uniform distributed loading for half of the girder to calculate the strain energy caused by bending moment:

For 0≤x≤a,

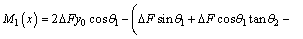
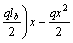                           (1)

For ,

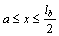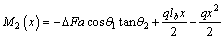        (2)

Considering the symmetry of structure and loading, the total strain energy equation is written as follows:

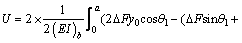
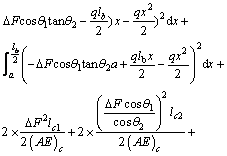
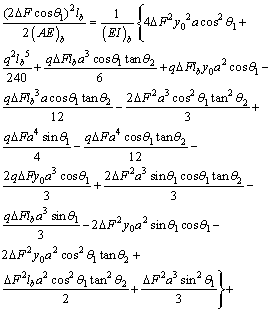
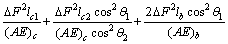    (3)

In order to calculate the increase in pre-tensioning force of each cable (△F) through the method of least work, the relation of total strain energy is differentiated with respect to △F and the obtained result is equated to zero:

                                (4)

The relation for calculating the increase of pre-tensioning force of each cable (△F) is obtained as follows:

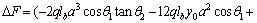
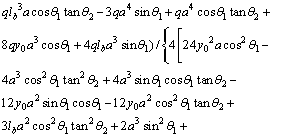
   (5)

where q is the intensity of uniform distributed load; l_b, l_C1 and l_C2 are the lengths of girder, first inclined cable (C₁) and second inclined cable (C₂), respectively; A_b and A_c are the cross sections of the girder and cable at both sides of the web, respectively; E_b and E_c are modulus of elasticity of the girder and cables, respectively; I_b is the moment of inertia of steel section; y₀ is the distance of neutral surface to the connection point of steel cable to the girder flanges (half of the height of girder web); and θ₁ and θ₂ are the angles between the first and second inclined cable and horizontal axis, respectively; a is the distance between the support and slope change region of the cable (horizontal projection of first inclined cable).

3.2 Calculating increase in pre-tensioning force of V-shaped steel cables in fixed supported girder bridge along with cable

In the fixed supported girder with V-shaped steel cables, as shown in Figure 3, assuming the increase in pre-tensioning force of steel cable to be equal to △F in the first slope part (C₁), the increase of pre-tensioning force of cable in the second slope part (C₂) is 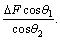Therefore, axial force of the girder is equal to 2△Fcosθ₁. It should also be mentioned that the fixed supported girder with the cables has two degrees of indeterminacy, the increase in pre-tensioning force of the cable (△F), and the moment at fixed end (M). To calculate the increase of pre-tensioning force of the cables as well as the moment at fixed end through the method of least work, the relation of total strain energy is differentiated with respect to each of them and the result is equated to zero resulting in the desired relations. Hence, bending moment of fixed supported girder along with V-shaped steel cables under uniform distributed loading is obtained for half of the girder so as to calculate the strain energy caused by bending as follows:

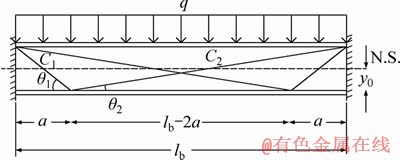
Figure 3 Fixed supported girder bridge along with V-shaped steel cables

For 0≤x≤a,

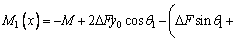
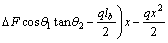             (6)

For ,

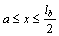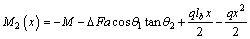     (7)

Considering the symmetry of structure and loading, the total strain energy equation is written as follows:

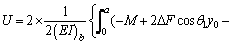
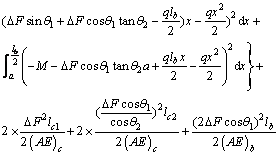
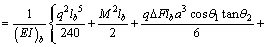
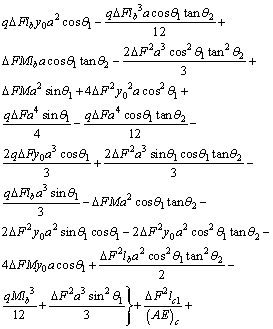
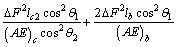            (8)

In order to calculate the moment at fixed end (M) through the method of least work, the relation of total strain energy is differentiated with respect to M and the obtained result is equated to zero:

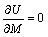                                (9)

The calculated bending moment at the fixed end (M) is obtained as follows:

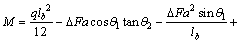
         (10)

In order to calculate the increase of pre- tensioning force of each cable (△F) through the method of least work, the relation of total strain energy is differentiated with respect to △F and the obtained result is equated to zero:

                             (11)

The calculated increase of pre-tensioning force of cables (△F) is obtained using Eq. (10) as follows:

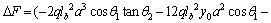
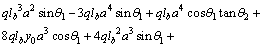
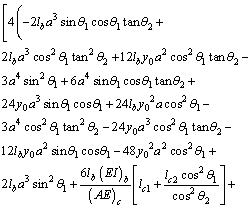
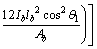                      (12)

If 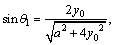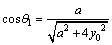and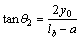(as shown in Figure 3) are replaced in Eq. (10), the moment at fixed end (M) is 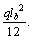This value is the moment at fixed end in girder without cable.

4 Deflection of girder bridge

The deflection of girder with different support conditions without cable and with V-shaped cables can be calculated by ignoring the effects of shear and axial forces using virtual work method.

4.1 Maximum deflection of simply supported and fixed supported girder bridges without cable under uniform distributed loading

If the length and flexural rigidity of the girder are l_b and (EI)_b, respectively, the maximum deflection of simply supported and fixed supported girders without cable under uniform distributed loading q are calculated as follows:

The deflection of the mid span of simply supported girder without cable:

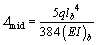                         (13)

The deflection of the mid span of fixed supported girder without cable:

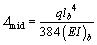                         (14)

4.2 Calculating maximum deflection of simply supported girder bridge along with V-shaped cables

Assuming the force of steel cable to be equal to F in the first inclined part (C₁), the force of cable in the second inclined part (C₂) is 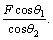Considering the symmetry of structure and loading (Figure 2), bending moment of simply supported girder along with V-shaped cables is obtained under real loading for the half of girder as follows:

For 0≤x≤a,

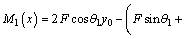
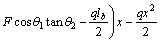             (15)

For ,

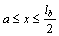        (16)

where F=F_pt+△F is the total force of the cable; F_pt is the initial pre-tensioning force of the cable; △F is the increase of pre-tensioning force of the cable.

In analyzing the structure under virtual loading, if the structure is indeterminate, its constraints can be eliminated up to being converted to a stable determinate structure. In the girder and cable system, the cable is a redundancy and can be omitted in analyzing the structure under virtual loading. The bending moment of simply supported girder is obtained under unit virtual load on mid span for half of the girder as follows:

For ,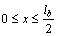

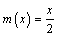                              (17)

Considering the symmetry of structure and loading, the deflection of the mid span of simply supported girder along with V-shaped cables is calculated as follows:

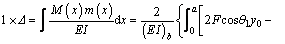
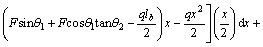
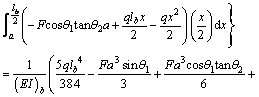
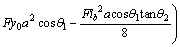          (18)

4.3 Calculating maximum deflection of fixed supported girder bridge along with V-shaped cables

Assuming the force of steel cable to be equal to F in the first inclined part (C₁), the force of cable in the second inclined part (C₂) is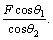 The moment at fixed end (M) is obtained as follows (as shown in Section 3.2):

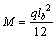                              (19)

The bending moment of fixed supported girder along with cable under real loading (Figure 3) is obtained for half of the girder as follows:

For 0≤x≤a,

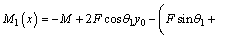
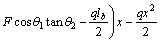             (20)

For ,

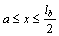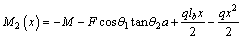
   (21)

The bending moment of fixed supported girder under unit virtual loading on mid span is obtained for half of the girder as follows:

For ,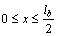

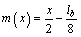                           (22)

The deflection of mid span of fixed supported girder along with cable is calculated as follows:

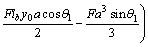               (23)

5 Finite element modeling of steel girder bridges pre-stressed with two V-shaped steel cables for calculating deflection

Simply supported and fixed supported girders have been designed based on load and resistance factor design (LRFD) method using AISC360-10 code [20]. Simply supported girder has been designed in such a way that the maximum deflection under dead and live loads is greater than the allowable deflection (1/240 of the girder length). However, due to the high stiffness of fixed supported girders, usually the maximum deflection is less than the allowable limit. Therefore, a fixed supported girder has been merely designed to show the effects of cable. Table 1 presents the properties of the girders with various support conditions as well as related allowable and the maximum deflections under service load. It should be noted that the length of loading span is 1.5 m for the girders with different support conditions; dead and live loads are 450 and 200 kg/m², respectively.

The girders are modeled in the finite element ABAQUS software under uniform distributed loads, considering different support conditions without cable and with V-shaped steel cables. Figure 4 presents finite element model of the girder along with the cable. The girders and cables have been modeled in 3-dimensional coordinate with shell and truss elements (as wire) respectively. The weld’s connector is used to connect the cable to the top flange of the girder at two ends providing a perfect connection between two nodes. Moreover, coupling constraint is used to connect the cables to the bottom flange of the girder so as to model the deviator’s behavior. Uniform distributed load is applied as a surface traction type on the top flange. Predefined field tool is used to create the initial pre-tensioning stress in the cables as well. The initial pre-tensioning stress is applied to the cable in ABAQUS software and uniform distributed loading is applied. Because the steel girder is not rigid and the cable creates the compression force and the steel girder length is decreased. So, a part of the initial pre-tensioning stress of cable is lost. Therefore, the amount of the initial pre-tensioning stress is considered to be greater in ABAQUS software to reach the desired pre-stressing value after its loss. Figure 5 presents the locations of cables in the girders with different support conditions.

Table 1 Properties and deflections of girders with different support conditions

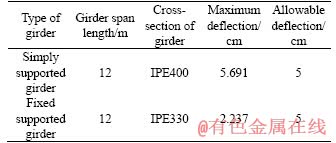
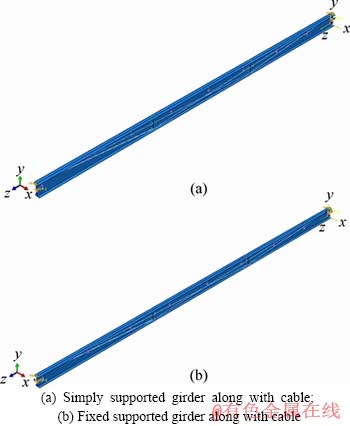
Figure 4 Finite element model of girder along with V-shaped cables:

Figure 5 Locations of two V-shaped steel cables in girders:

For better presenting the behavior of girder with V-shaped cables and different support conditions, first it has been modeled in the software without cable, and then with cables; and the obtained results have been compared with each other. The materials of girder and cables are defined as linearly elastic in the software. The steel material of girders considered in this research is ST-37; yield stress is 240 MPa; modulus of elasticity of steel is 200 GPa; Poisson ratio is 0.3; density of steel is 7850 kg/m³. The material of steel cable is in accordance with ASTM A416M standard [21]. 7-wire strand is considered for steel cable with low relaxation, elasticity module of 28.5×10⁶ psi (196501.8 MPa) and Poisson ratio of 0.3.

6 Verification of theoretical relations of deflection with results of ABAQUS models

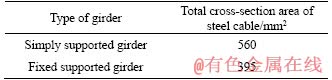
Static general analysis of ABAQUS software has been used to analyze the girders with different support conditions (Table 1), without cable and with cables. The cross-sectional area of steel cables is considered 7-wire strand with low relaxation for simply supported and fixed supported girders with equal numbers of cables at both sides of the webs with the cross section areas of 140 mm² and 98.71 mm², for each cable, respectively. These values are considered according to ASTM A416 standard and presented in Table 2. Pre-tensioning of the steel cable is considered 600 MPa. Controlling the accuracy of theoretical relations, the maximum deflections obtained from modeling are compared to those of the theoretical relations for the girders with V-shaped cables and with different support conditions.

Table 2 Cross-sectional area of V-shaped steel cables for girders with different support conditions

The results of the maximum deflection obtained from modeling are compared with those of Eqs. (13) and (18) for simply supported girders without cable and with cable and with those of Eqs. (14) and (23) for fixed supported girders without cable and with cable, as listed in Table 3.

As shown in Table 3, the maximum deflection of the girder without cable obtained from modeling is slightly more than that of theoretical relations. The reason is that the girder has been modeled in ABAQUS software in the form of shell; and therefore girder haunch cannot be modeled. The maximum deflection of the girder along with V-shaped cables, obtained from modeling, is very close to that of theoretical equations. Considering the theoretical relations of increasing the pre-tensioning force of each cable, reducing the moment of inertia in ABAQUS software due to not modeling the girder haunch results in obtaining more increase in the pre-tensioning force in modeling than that of theoretical equations. Consequently, the steel girder deflection related to the increase in pre-tensioning force of the cables, obtained from modeling, is slightly more than that of theoretical relations. Therefore, in calculating the deflections of girders along with V-shaped steel cables and different support conditions, the errors arise from different deflections of the girders along with the cables, related to the status of increasing in pre-tensioning force of the cable, obtained from modeling and those of theoretical equations operate as opposed to that of the girder without cable related to the uniform distributed loading. Consequently, they cancel out the effects of each other.

Bending moment caused by cable force is in the opposite direction of bending moment due to uniform distributed loading. As presented in Table 3, the maximum deflection of the girder along with pre-stressed cables is less than that of the girder without cable. Moreover, the maximum deflection is less than allowable limit in simply supported girders. Therefore, using the cables satisfies the deflection criterion under service load.

7 Effect of length a on maximum deflection of simply supported and fixed supported girder bridges along with V-shaped steel cables

Equations (18) and (23) are considered to calculate the maximum deflections of simply supported and fixed supported girders along with the V-shaped cables according to Table 1 for simply supported and fixed supported, Table 2 for cross-section of steel cable, and a of Figures 2 and 3 for different values of the distance from support. Figures 6 and 7 depict the curves of the maximum deflection for simply supported and fixed supported girders along with V-shaped steel cables for various distances from support (a) for half of the girder.

According to Figures 6 and 7, if a is zero in the simply supported as well as fixed supported girders along with the cables, their maximum deflections are 5.691 cm and 2.237 cm, respectively. These values are the results of the maximum deflections of simply supported and fixed supported girders without cable (Table 3). The reason is that for keeping the bending moment in the slope change region of cable continuous, the horizontal component of the force of first inclined cable from the left side (C₁) should be equal to the horizontal component of the force of second inclined cable from the left side (C₂). Therefore, if the first inclined cable from the left side (C₁) becomes vertical in its special status (in the case a is zero), the horizontal component of vertical cable force becomes equal to zero; and consequently, the horizontal component of the force of second inclined cable from the left side (C₂) becomes zero. As the length of vertical cable which is equal to the distance between two flanges of the girder remains constant, no force is created in the length of cable. Therefore, the cable has no effect on the girder behavior; and the girder deflection is exactly the same as that of the girder without cable. Then, maximum deflection reduces with increasing in the distance from support (a). Finally, for half length of the girder, the maximum deflections are the minimum; 4.016 cm and 0.286 cm, respectively, in the simply supported and fixed supported girder along with the cable.

Table 3 Maximum deflection values obtained from modeling and theoretical equations for girders with different support conditions without cable and with V-shaped steel cables

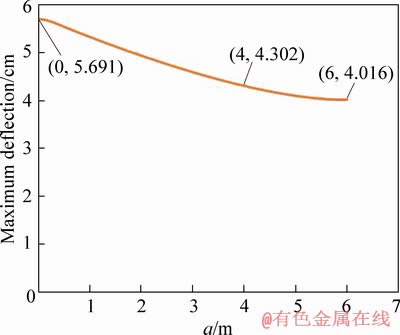
Figure 6 Maximum deflection of simply supported girder along with V-shaped steel cables for different values of distance from support (a) for half of the girder

Figure 7 Maximum deflection of fixed supported girder along with V-shaped steel cables for different values of distance from support (a) for half of the girder

8 Comparison of bending moment diagrams of girder bridges without cable and with V-shaped steel cables

The bending moment diagrams of the girders with different support conditions without cable and with V-shaped steel cables are plotted and compared for the girders presented in Table 1. The total cross-section areas of steel cables are according to Table 2 and pre-tensioning stress of steel cables is assumed 600 MPa.

8.1 Comparison of bending moment diagrams of simply supported girder bridge without cable and with V-shaped steel cables

The bending moment diagrams of simply supported girders without cable and with V-shaped cables are plotted based on Eqs. (15) and (16) and are depicted in Figure 8.

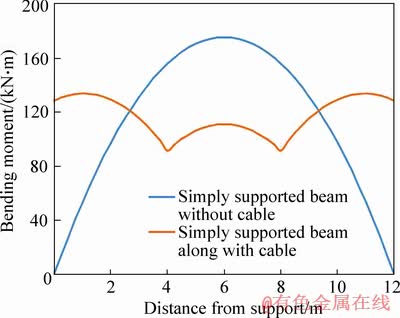
Figure 8 Bending moment diagrams of simply supported girder without cable and with V-shaped cables

As shown in Figure 8, the bending moment of simply supported girder with cable is increased compared to that of simply supported girder without cable from each support to the location of the bending moment being equal in simply supported girder with V-shaped steel cables and without cable and then is decreased between two locations of the bending moment being equal in simply supported girder with cables and without cable.

8.2 Comparison of bending moment diagrams of fixed supported girder bridge without cable and with V-shaped steel cables

The bending moment diagrams of fixed supported girders without cable and with V-shaped cables are plotted based on Eqs. (20) and (21) and are depicted in Figure 9:As shown in Figure 9, the bending moment of fixed supported girder with V-shaped steel cables is decreased compared to that of fixed supported girder without cable.

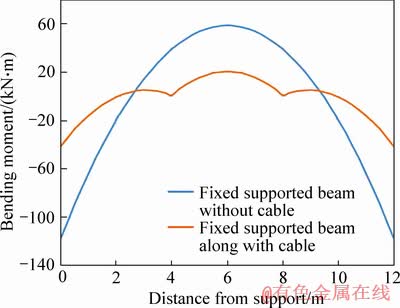
Figure 9 Bending moment diagrams of fixed supported girder without cable and with V-shaped steel cables

9 Conclusions

Cables, due to their low weights, small cross sections, and high tensile strengths, are reckoned as proper alternatives for pre-tensioning long steel girders subjected to uniform distributed loads. In this research, cables are employed to pre-stress the girder bridges with different support conditions in which the deflection is not within the allowable range, despite appropriate design under bending and shear. Theoretical equations have been derived to calculate the increase in pre-tensioning force of the V-shaped steel cables, the deflection of simply supported and fixed supported girders with and without cables. The results obtained from the finite element model and theoretical equations, are briefly summarized as follows:

1) The moment at fixed end in fixed supported girder along with V-shaped steel cables is independent of total force of the cables.

2) Adding cables to the girder results in reducing the deflection of girder with different support conditions. Comparing the results obtained from theoretical equations and those of finite element model demonstrates that the theoretical equations developed in this article can properly predict the deflection of simply supported and fixed supported without cable and with V-shaped steel cables.

3) The effects of length a, on the maximum deflection of simply supported and fixed supported girders along with the V-shaped cables have been studied. According to the obtained results, if a is equal to zero, the maximum deflection of girder without cable is obtained. If the distance from support (a) increases, maximum deflection decreases; and finally, for half length of the girder, maximum deflection is minimum.

4) The bending moment diagrams show that in simply and fixed supported girders along with V-shaped steel cables, cables reduce the bending moment of girder compared to those of simply and fixed supported girders without cable.

References

[1] RAZAVI M, SHEIDAII M R. Seismic performance of cable zipper-braced frames [J]. Journal of Constructional Steel Research, 2012, 74: 49-57. DOI: 10.1016/j.jcsr.2012.02.007.

[2] HOU Xing-guo, TAGAWA H. Displacement-restraint bracing for seismic retrofit of steel moment frames [J]. Journal of Constructional Steel research, 2009, 65: 1096-1104. DOI: 10.1016/j.jcsr.2008.11.008.

[3] FANAIE N, AGHAJANI S, AFSAR DIZAJ E. Theoretical assessment of the behavior of cable bracing system with central steel cylinder [J]. Advances in Structural Engineering, 2016, 19(3): 463-472. DOI: 10.1177/ 1369433216630052.

[4] FANAIE N, AGHAJANI S, AFSAR DIZAJ E. Strengthening of moment-resisting frame using cable–cylinder bracing [J]. Advances in Structural Engineering, 2016, 19(11): 1-19. DOI: 10.1177/1369433216649382.

[5] GIACCU G F. An equivalent frequency approach for determining non-linear effects on pre-tensioned-cable cross-braced structures [J]. Journal of Sound and Vibration, 2018, 422: 62-78. DOI: 10.1016/j.jsv.2018.02.016.

[6] TROITSKY M S. Prestressed steel bridges—Theory and design [M]. New York: Van Nostrand Reinhold, 1990.

[7] AYYUB B M, SOHN Y G, SAADATMANESH H. Prestressed composite girders under positive moment [J]. Journal of Structural Engineering, 1990, 116(11): 2931-2951. DOI: https://doi.org/10.1061/(ASCE)0733-9445(1990)116: 11(2931).

[8] AYYUB B M, SOHN Y G, SAADATMANESH H. Prestressed composite girders. II: Analytical study for negative moment [J]. Journal of Structural Engineering, 1992, 118(10): 2763-2782. DOI: https://doi.org/10.1061/(ASCE) 0733-9445(1992)118:10(2763).

[9] NIE J G, CAI C S, ZHOU T R, LI Y. Experimental and analytical study of prestressed steel–concrete composite beams considering slip effect [J]. Journal of Structural Engineering, 2007, 133(4): 530-540. DOI: 10.1061/(ASCE) 0733-9445(2007)133:4(530).

[10] ZHOU Huan-ting, LI Shao-yuan, CHEN Lu, ZHANG Chao. Fire tests on composite steel-concrete beams prestressed with external tendons [J]. Journal of Constructional Steel Research, 2018, 143: 62-71. DOI: https://doi.org/10.1016/ j.jcsr.2017.12.008.

[11] BELLETTI B, GASPERI A. Behavior of prestressed steel beams [J]. Journal of Structural Engineering, 2010, 136(9): 1131-1139. DOI: 10.1061/(ASCE)ST.1943-541X.0000208.

[12] PARK S, KIM T, KIM K, HONG S N. Flexural behavior of steel I-beam prestressed with externally unbonded tendons [J]. Journal of Constructional Steel Research, 2010, 66: 125-132. DOI: 10.1016/j.jcsr.2009.07.013.

[13] KAMBAL M E M, JIA Yan-min. Theoretical and experimental study on flexural behavior of prestressed steel plate girders [J]. Journal of Constructional Steel Research, 2018, 142: 5-16. DOI: https://doi.org/10. 1016/j.jcsr.2017.12.007.

[14] ZHANG Wen-fu. Symmetric and antisymmetric lateral- torsional buckling of prestressed steel I-beams [J]. Thin-walled Structures, 2018, 122: 463-479. DOI: http://dx. doi.org/10.1016/j.tws.2017.10.015.

[15] NOBLE D, NOGAL M, O’CONNOR A, PAKRASHI V. Dynamic impact testing on post-tensioned steel rectangular hollow sections: An investigation into the “compression-softening” effect [J]. Journal of Sound and Vibration, 2015, 355: 246-263. DOI: http://dx.doi.org/10. 1016/j.jsv.2015.06.021.

[16] CAO Liang, LIU Jie-peng, CHEN Y Frank. Vibration performance of arch prestressed concrete truss girder under impulse excitation [J]. Engineering Structures, 2018, 165: 386-395. DOI: https://doi.org/10.1016/j.engstruct.2018.03. 050.

[17] MIYAMOTO A, TEI K, NAKAMURA H, BULL J W. Behavior of prestressed beam strengthened with external tendons [J]. Journal of Structural Engineering, 2000, 126(9): 1033-1044. DOI: https://doi.org/10.1061/(ASCE)0733-9445 (2000)126:9(1033)

[18] PARK Y H, PARK C W, PARK Y G. The behavior of an in-service plate girder bridge strengthened with external prestressing tendons [J]. Engineering Structures, 2005, 27: 379-386. DOI:10.1016/j.engstruct.2004.10.014.

[19] REN Wei-xin, CHEN Gang, HU Wei-hua. Empirical formulas to determine cable tension using fundamental frequency [J]. Structural Engineering and Mechanics, 2005, 20(3): 363-380. DOI: https://doi.org/10.12989/sem.2005. 20.3.363.

[20] American Institute of Steel Construction (AISC) ANSI/AISC360–10: Specification for structural steel buildings [S]. Chicago, IL, 2010.

[21] American Society for Testing and Materials (ASTM): Standard specification for low-relaxation, seven-wire steel strand for prestressed concrete (ASTM A416M) [S]. Philadelphia, PA.

(Edited by YANG Hua)

中文导读

使用两个V形预张拉电缆对长钢I型梁桥的挠度控制

摘要：尽管对梁在弯曲和剪切作用下的设计合理，但钢梁的挠度往往超过允许范围，因此结构设计人员在这方面遇到了挑战。考虑到拉索重量轻、截面小、抗拉强度高等特点，采用拉索来控制长梁桥的挠度，而不是提高其高度。建立了计算V形钢索在外荷载作用下的预张力的理论关系式，并计算了V形索和不同支承条件下钢梁桥的挠度。为验证理论关系，采用ABAQUS有限元软件，在无索和有V形索的情况下，对钢梁桥进行有限元建模。结果表明，所建立的理论关系式能够较好地预测V形索梁桥在不同支护条件下的挠度。另外，还研究了简支梁桥和固定梁桥中跨间距对跨中挠度的影响，得出了最小挠度与支座之间的适当距离。

关键词：挠度；钢桥；I形梁；V形索；预张拉；最小功

Received date: 2018-06-01; Accepted date: 2019-07-11

Corresponding author: Nader FANAIE, PhD, Associate Professor; Tel: +98-21-88779623; Mobile No: +989123449961; E-mail: fanaie@kntu.ac.ir; ORCID: 0000-0002-6789-8930