ARTICLE

J. Cent. South Univ. (2019) 26: 2041-2055

DOI: https://doi.org/10.1007/s11771-019-4152-1

Quantitative analysis on influencing factors for interface propagation-based thermal conductivity measurement method during solid-liquid transition

ZHOU Tian(周天), MA Xiao-yi(马筱艺), LIU Xu(刘旭), LI Yuan(李远)

School of Energy Science and Engineering, Central South University, Changsha 410083, China

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019

Abstract: The recently proposed interface propagation-based method has shown its advantages in obtaining the thermal conductivity of phase change materials during solid-liquid transition over conventional techniques. However, in previous investigation, the analysis on the measurement error was qualitative and only focused on the total effects on the measurement without decoupling the influencing factors. This paper discusses the effects of influencing factors on the measurement results for the interface propagation-based method. Numerical simulations were performed to explore the influencing factors, namely model simplification, subcooling and natural convection, along with their impact on the measurement process and corresponding measurement results. The numerical solutions were provided in terms of moving curves of the solid-liquid interface and the predicted values of thermal conductivity. Results indicated that the impact of simplified model was strongly dependent on Stefan number of the melting process. The degree of subcooling would lead to underestimated values for thermal conductivity prediction. The natural convection would intensify the heat transfer rate in the liquid region, thereby overestimating the obtained results of thermal conductivity. Correlations and experimental guidelines are provided. The relative errors are limited in ±1.5%, ±3%and ±2% corresponding to the impact of simplified model, subcooling and natural convection, respectively.

Key words: phase change material; thermal conductivity measurement; influencing factor; interface propagation-based method; numerical simulation

Cite this article as: ZHOU Tian, MA Xiao-yi, LIU Xu, LI Yuan. Quantitative analysis on influencing factors for interface propagation-based thermal conductivity measurement method during solid-liquid transition [J]. Journal of Central South University, 2019, 26(8): 2041-2055. DOI: https://doi.org/10.1007/s11771-019-4152-1.

1 Introduction

Heat transfer process for phase change materials (PCMs) during solid-liquid transition has attracted considerable attention for scientists and engineers in last twenty years. This is driven by the fact that the advantages of such materials are numerous, i.e. narrow melting temperature span, large heat storage capacity, almost isothermal energy charge/discharge process as well as diverse melting temperature. PCMs are widely adopted in many engineering applications such as renewable energy utilization [1, 2], building energy conservation [3, 4], latent heat thermal storage (LHTES) [5, 6], and electronics thermal management. Up to now, we have seen an increasing interest of PCMs and their applications due to the environmental concerns that come from fossil energy consumption and its aftermaths. Because the heat transfer rate as well as the degree of phase change during a melting or solidification process is determined largely by the thermal physical properties of the PCMs, obtaining accurate values of such transport properties of PCMs is very important for the feasibility of the PCMs in engineering applications.

According to Fourier’s Law, thermal conductivity can be determined from the quantitative relation between the relevant thermal penetration and the temperature gradient of the specimen, and a variety of well-established conventional measurement techniques were proposed and developed which can be categorized as transient and steady method. Transient method is the preferred thermal conductivity measurement technique for PCMs due to their advantages in terms of high accuracy, wide measurement range and time-saving [7-9]. Among these, transient plane source (TPS) [10-13] and transient hot wire (THW) [14-17] method are widely adopted by many researchers to investigate the thermal conductivity of PCMs. However, it has been reported that when measuring thermal conductivity of PCMs involving solid to liquid phase change process by THW or TPS, the test results for both solid and liquid PCMs demonstrate a strong dependence on the initial temperature of the sample, and move toward to the value of thermal conductivity of liquid PCM [18, 19]. The reason for those “anomalous” results is that THW and TPS measurement techniques are both based on the one-dimensional heat conduction problem for homogenous medium (CARSLAW and JAEGER [20]). However, when the temperature approaches the melting point during the test, the PCM starts turning into two distinct phases, and the original homogenous medium transforms into a composite medium. The onset of phase change process obviously violates the applicable conditions of THW and TPS. As a result, operation of the THW and TPS under PCMs phase transition process is not consistent with the theoretical model based on which THW and TPS are designed, and relevant measurement results are therefore inaccurate any longer.

In light of the need for the benchmark of PCMs’ thermal conductivity during phase transition, some unconventional measurement methods have been established recently [21]. ZHANG et al [22] proposed a temperature-history method, which can obtain the PCMs’ thermal conductivity, fusion heat and heat capacity simultaneously. The time- dependent temperature curves of the sample during the phase change process are compared with those of a well-known reference sample, and lumped capacity model is then used to calculate corresponding thermal physical properties of the sample. The deviation between the temperature- history measurement results and the literature values are less than 10%. ZHANG et al [23] developed improved THW method to investigate the thermal conductivity of PCM slurry subject to the process of phase change. An improved measurement model was proposed, and the effect of phase change on the measurement was numerically analyzed. It is found that the phase change process will enhance heat transfer rate, therefore the real value of the thermal conductivity of the sample is smaller than those obtained directly from the conventional THW methods. O’CNNOR et al [24] determined the best path to prediction (BPP) for the thermal properties of five organic PCM in liquid state near the melting point. Different BPPs were calibrated for alkanes based on heneicosane and unsaturated acids and the tested results for thermal physical properties of such materials show agreement with reported values within 15%.

Recently, ZHOU et al [25] presented a dynamic technique, namely interface propagation- based method, to explore the thermal conductivity of liquid PCMs near melting temperature. The thermal conductivity can be obtained from the transient moving features of the interface in a Stefan melting process. Also, the author concluded that the inconsistencies on the boundary conditions between the theoretical and the experimental melting process are the reasons for the measurement error. Although, ZHOU et al [25] pointed out the major influencing factors for the interface-propagation method and calibrated the measurement results numerically, but further understanding of such factors’ influencing mechanisms is still lacking. As a result, the purpose of the present study is to provide further understanding on the underlying mechanisms of influencing factors which affect the measurement results for the interface propagation-based method. These kinds of information can help to improve the test accuracy in terms of calibrated experimental conditions and operations of the interface propagation-based method. In this paper, we first gave a brief introduction on the interface propagation-based thermal conductivity measurement approach [25]. Next, we quantitatively evaluated, by numerical simulation, the measurement errors induced by the three influencing factors: measurement model simplification, subcooling and natural convection. Finally, the correlation equations for improving the accuracy of the measurement were presented, as well as the experimental operation guidelines for mitigating the measurement errors.

2 Problem statement

Since the goal of this study is to analyze the effects of influencing factors on the measurement results of the PCMs’ thermal conductivity based on the interface-propagation method, it is necessary to briefly introduce the fundamentals of this method.

As shown in Figure 1, we suppose an infinite long cylinder which contains solid PCM. In the initial state, the solid-state PCM is kept at its melting point (T_m). Then, at the zero moment of time (τ=0), the temperature at the boundary (r=R) of the cylinder is instantaneously raised to a higher temperature (T₀). With the sharp change of the boundary temperature, the solid PCM starts to thaw, and a distinct interface is emerged at the peripheral of the cylinder and moves along the radial direction as the phase change proceed. The governing equations for such phase change process can be formulated as follows:

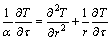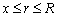,              (1)

with the boundary conditions:

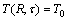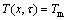,                    (2)

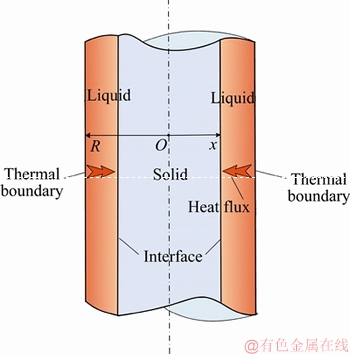
Figure 1 Schematic diagram of Stefan melting process in cylindrical coordinate

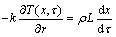                       (3)

where α and T represent the thermal diffusivity of the PCM and temperature variable, respectively; r is the cylindrical coordinate; R is the radius of the cylinder; k, ρ and L are the thermal conductivity of the liquid PCM, density, and the Latent heat, respectively; x is the position variable of the interface during the melting.

By using the Bessel function and the Laplace transformation method, the analytical solution of Eqs. (1) to (3) can be derived, and the dimensionless form of the moving speed of the interface is obtained, as depicted in Eq. (4). The detailed deducing procedure can be found in Ref. [25].

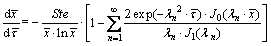  (4)

Since the summation term in Eq. (4) is much less than 1 as the number of n goes to infinite, it can be neglected and Eq. (4) can be simplified as

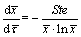                            (5)

Equation (5) is then solved and the thermal conductivity of the liquid PCM is

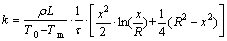        (6)

Equation (6) reveals the explicit correlation between the instantaneous position of the interface (x) and the thermal conductivity of the liquid PCM (k) along with the heat of fusion (H) and density (ρ) of the PCM under the Stefan melting process (T₀, T_m). Hence, Eq. (6) can be used as the measurement model for thermal conductivity of the PCM, and the input variable is the instantaneous position of the interface (x(τ)), which can be represented by the thickness of the liquid in the melting process.

Based on the above proposed measurement model, a well-designed testing system was established, which is presented schematically shown in Figure 2. An aluminum cylinder, serving as the PCM container, was manufactured, with the height of 200 mm and radius of 44 mm. Six holes were drilled from the top of the container’s wall. Thermocouples were inserted and fixed in place into these holes to monitor the temperature variations of the Stefan boundary during the test. A flexible resistive heater was wrapped around the cylinder, providing the appropriate temperature boundary conditions required by the measurement model. During the test, the boundary condition (constant wall temperature) was achieved through the resistive heater with aid of PID control, and the temperature information from the thermocouples during the experiment was recorded by a data recorder. The instantaneous locations of the interface were measured through a fixed vernier caliper, by measuring the diameter of the solid sample during the test. The heat loss was calculated using temperature readings from thermocouples fixed at different locations in the top wall, and it was determined that no more than 6% of the total heat was provided by the heater transferred through the top wall. In the test, sodium acetate trihydrate (NaCH₃COO·3H₂O) was chosen as the sample to validate the viability of the proposed method. The properties of the test material are listed in Table 1.

The dimensionless values of the experimental results are presented in Figure 3. SteFo number is chosen to be the time scale for the abscissa, while the dimensionless measured thermal conductivity is set to be the ordinate, which was defined as:

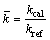                                (7)

where k_cal is the obtained value of thermal conductivity from the experiments and k_ref is the literature value of the tested PCM. From Figure 3

we can see that the experimentally determined thermal conductivity values are smaller than literature values by 5%-10% at the early stage of the experiment. While as the melting progressed, the values of 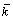show a monotonic increasing trend. ZHOU et al [25] concluded that there are three major influencing factors that would affect the thermal conductivity measurement, namely subcooling, model simplification and the onset of natural convection. The effects of such influencing factors on the predicted thermal conductivity values are discussed as hereunder:

1) Subcooling

According to the application requirement of measurement model, the entire solid PCM should be kept at melting point T_m before the onset of experiment. But it is nearly impossible to achieve such subtle equilibrium state (PCM must be maintained in solid state while be kept at melting temperature) in the real test. Therefore, the initial temperature of the solid PCM, denoted as T_i, was set to be a little bit lower than T_m before the test, for example 1 °C below the melting temperature T_m. Thus, the phenomenon of subcooling is introduced into the experiment, and the degree of subcooling will affect the experimental determined values of the thermal conductivity. The dimensionless form of degree of subcooling is formulated as Sc=(T_m-T_i)/(T₀-T_m).

2) Measurement model’s simplification

The real measurement model is presented in Eq. (4). One can see that Eq. (4) is a transcendental equation since it contains a summation term of the Bessel function. For the purpose of simplicity, the summation term in Eq. (4) was neglected since it is an infinitesimal amount, and the final measurement model was simplified as Eq. (6). However, the summation term stands for the transient thermal disturbance from the thermal boundary, and neglecting of such term will induce systematical errors in the measurement.

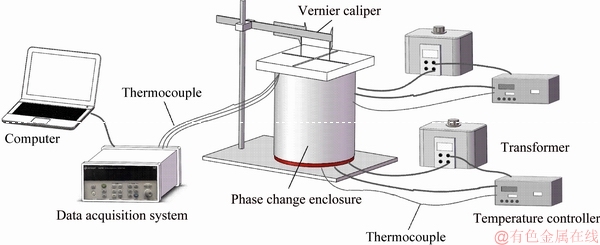
Figure 2 Schematic of testing system

Table 1 Properties of NaCH₃COO·3H₂O [26, 27]

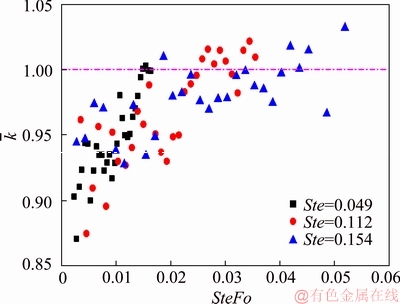
Figure 3 Experimental determined values of thermal conductivity as function of time for different boundary conditions [25]

3) Natural convection

The theoretical foundation of the measurement model is based on the pure heat conduction theory, which means that the heat transfer mechanism of natural convection was ignored when establishing the measurement model. But in reality, the natural convection substantially exists in the liquid region due to the combined effect of temperature difference and gravitational force. The onset of natural convention will augment heat transfer rate during the melting compared to that of the pure conduction controlled melting process, and therefore influence the experimentally obtained values of thermal conductivity.

Overall, upon the combining effects of above mentioned influencing factors, the values are underestimated from the beginning of the test, and decrease as the melting proceed. However, in previous study by ZHOU et al [25], they only qualitatively analyzed the effect of such influencing factors on the predicted thermal conductivity values. General and quantitative insight into the errors is still lacking, which requires more quantitative and explicit analysis. As a result, in the present study, issues related to affecting the measurement results of thermal conductivity are quantitatively analyzed by adopting computational methodologies.

3 Computational methodology

The numerical model was considered three-dimensional and the governing equations of the computational domain can be expressed as follows.

Continuity,

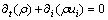                        (8)

Momentum,

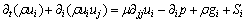      (9)

Energy,

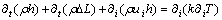        (10)

where u_i and μ represent the velocity and the dynamic viscosity of the liquid PCM, respectively; ρ is the density of the liquid PCM; p and g are the pressure and gravitational acceleration, respectively; h is the sensible enthalpy; ΔL is the latent heat; S_i represents the source term.

The enthalpy method was used to describe the phase change process since their maturity and accuracy were sufficiently proved by many researchers [18, 19, 26-28], especially for the phase change problem in lower Stefan number. Hence, the sensible enthalpy term h in Eq. (9) is defined as:

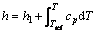                         (11)

where h₁ is the reference enthalpy; T_ref is the reference temperature; c_p is the specific heat capacity of the PCM. The latent heat content ΔL in Eq. (10) is defined as:

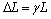                               (12)

where γ is the thermal expansion coefficient of PCM.

According to the enthalpy method, the liquid faction is defined as:

  (13)

The momentum sink term S_i in Eq. (9) is defined as

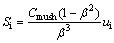                      (14)

where C_mush is damping constant of the mushy zone during the phase change process, which was set to 105 according to previous study [28].

The numerical solutions were obtained by ANSYS Fluent. According to the independence study, the grid number was set to be approximate 2.6×10⁶. In computation, the SIMPLE algorithm was chosen for solving the governing equations. The second order discretization scheme was adopted for momentum and energy; the standard discretization scheme was used for pressure; the time step size was set to be 0.01 s. The simulation was deemed convergent for each time step when the residues of the continuity and momentum were less than 10^-4, and that of energy was less than 10^-8.

4 Results and discussion

In this section, we first present the validation of the numerical model by comparing the simulation and the experimental results. Then, series parametric studies are performed, and the aim is to explore the effects of the influencing factors on the predicted thermal conductivity values of the liquid PCM.

4.1 Validation of numerical model

Sodium acetate trihydrate (NaCH₃COO·3H₂O) was chosen as the sample for the validation of the numerical model, whose thermal properties are summarized in Table 1. Figure 4 shows the experimental and numerically determined results in terms of dimensionless interfaces location versus melting time, with the Stefan number of 0.05 and 0.16. One can see that both experimental and numerical determined interface’s moving characteristics exhibit a non-linear trend and are in very good agreement with each other. Therefore, it can be concluded that the numerical model yields valid results both qualitatively and quantitatively.

4.2 Strategy of parametric study

As mentioned earlier, due to the practical difficulties in experimental implementation and the contradictions in melting features between the theoretical and the experimental melting processes, the existence of the influencing factors and their aftermath will introduce errors into the measurement values of the thermal conductivity. Hence, series numerical studies were performed to investigate the quantitative insight into the measurement uncertainties, thereby providing guidelines for mitigating the effects of the influencing factors on the measurement results. The concept and the strategy of the parametric study are explained by the flowchart as shown in Figure 5.

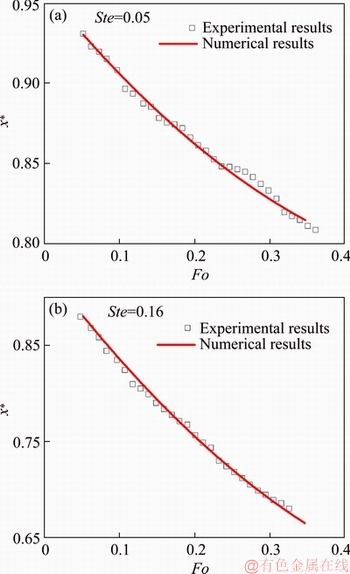
Figure 4 Comparison of experimentally and numerically obtained interface locations for NaCH₃COO·3H₂O

The key ideal of the parametric study is that the influencing factors’ effects on the melting behavior of the experiments were obtained by numerical simulations, which is quite time-saving compared to running real experiments. In the simulation, sodium acetate trihydrate (NaCH₃COO·3H₂O) was chosen as the sample, whose property is summarized in Table 1, and the effects of the influencing factors were also considered. We can see from Figure 5 that series interface’s moving curves were obtained numerically, whose detailed moving characteristics were affected by corresponding influencing factors, model simplification, subcooling and natural convection, respectively. These numerically determined instantaneous positions of the interface were used as the input variables of the measurement model, and series values of the thermal conductivity of the PCM k_num could be subsequently obtained by Eq. (6). Due to the effect of the influencing factors, the obtained values of k_num would deviate from the initially assigned value (also refers to reference value) of k_ref to some extent. Furthermore, those differences between k_num and k_ref, and their variation feature during the melting process, are the direct representation of the effects on the measurement results under the influence of such factors. As a result, by comparing the values of k_num and k_ref, the effects of the influencing factors can then be formulized qualitatively through regression analysis. In the following section, the influencing factors and their impact on the measurement results were investigated in turn.

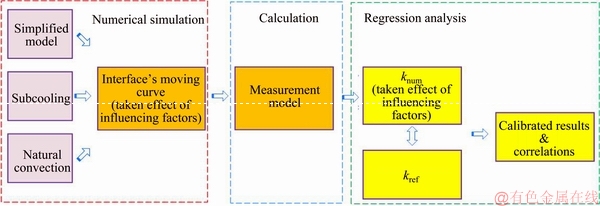
Figure 5 Flowchart of parametric study

4.3 Effect of model simplification on predicted thermal conductivity

Numerically determined moving curves of the interface were first compared with those of theoretical prediction Eq. (6). Eight cases were solved for different final boundary temperature (T₀), with the value of 338, 339, 340, up to 345 K. The corresponding Stefan numbers are 0.09, 0.10, 0.11, 0.12, 0.14, 0.15, 0.16 and 0.17. The results are presented in the dimensionless form as shown in Figure 6, where Fourier number (Fo) represents the dimensionless time and the dimensionless position is defined as

                                (15)

where x=x(τ) is the position variable of the interface; r₀ is radius of the cylindrical enclosure. From Figure 6, one can see that the instantaneous positions of the numerically obtained interfaces are smaller than those of theoretically obtained results for Ste=0.09, 0.10, 0.11, 0.12, and the extent of such tendency is also increased as the melting progresses. While for Ste=0.14, 0.15, 0.16 and 0.17, the differences between the numerically and theoretically obtained interfaces’ moving curves present the opposite behavior. The numerically determined interfaces’ locations are comparatively larger than the theoretical results, and those deviations also increase as time elapses. Hence, we can conclude that due to the impact of the simplification on the measurement model, the theoretically predicted results demonstrate an altered melting process; the displacement rate of the interface is smaller than the numerically determined “real melting rate” for Stefan number below 0.13. But this phenomenon is reversed when the Stefan number exceeding 0.13. Figure 7 presents the averaged deviations of the interface’s position between the numerical and theoretical solution for conditions corresponding to 8 different Stefan number. One can see that the deviation shows strong dependence on the Stefan number. When Ste<0.13, the deviation decreases strictly monotonously with the increasing Stefan number. When Ste>0.13, an increasing trend of the deviations is found. It should be noted that this transition of regime is a rough estimation since only 8 conditions of Stefan number were investigated in the present study.

To reveal the impact on the thermal conductivity prediction under the effect of model simplification, we substituted the numerically determined interfaces’ curve into Eq. (6). For eight studied cases, the dimensionless values of thermal conductivity calculated through Eq. (6) and are plotted against the dimensionless melting time as shown in Figure 8. The dimensionless thermal conductivity is defined as k^*=k/k_ref, where k is the value determined from numerical studies and k_ref is the reference value (also refers to initially assigned value in simulation). Comparing to the reference value k_ref, the impact of the model simplification is represented in terms of overestimations on the values of k for Ste=0.09, 0.10, 0.11 and 0.12, while for Ste=0.14, 0.15, 0.16 and 0.17, predictions of the values of k are underestimated. This behavior is consistent with that exhibited in Figures 6 and 7. The maximum error of the predicted value is found to be ±4% compared to the reference value. Another feature of Figure 8 is that predicted value of k demonstrates a monotonic increasing trend with the increasing of the melting time for all cases, and the relative deviation is approximately to be 1.5%.

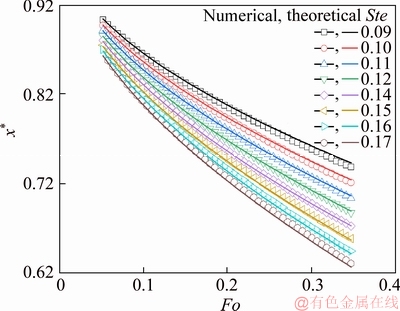
Figure 6 Comparison between numerically and theoretically determined interfaces’ moving curve

Figure 7 Averaged deviation between numerically and theoretically determined interfaces’ moving curve

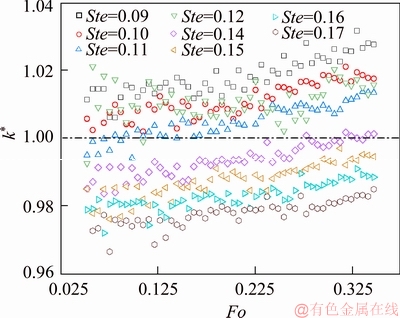
Figure 8 Predicted thermal conductivity values under influence of model simplification

By using the numerical results as the database, a correlation was obtained to mitigate the impact of model simplification. Since the final boundary temperature and the melting time both affected the measurement results, Stefan and Fourier numbers are therefore adopted through following formulation.

k′/k=1.142Fo^-0.0169Ste^0.076                            (16)

where k′ is the calibrated value of thermal conductivity. It is found that the dependency on Stefan number is stronger than Fourier number. The calibrated values of thermal conductivity through Eq. (15) are displayed in Figure 9. We can see that the empirical correlation mitigates the impact of the model simplification, by limiting the measurement errors within the range of ±1.8%. Also, the suggested measurement time range is 0.8≤Fo≤1.4, since the dimensionless measurement error is limited in ±1.5% during this time interval. The valid range for the proposed correlation is 0≤Ste≤2 and 0≤Fo≤0.35.

Figure 9 Calibrated thermal conductivity values under influence of model simplification

4.4 Effect of subcooling on predicted thermal conductivity

The dependence of the interface’s moving behavior and the corresponding obtained thermal conductivities on the effect of subcooling was investigated numerically. Thermal conductivity values and interface’s moving curves for 36 cases were obtained with the Stefan number ranging from 0.1 to 0.17, and the degree of subcooling from 0 to 1, respectively. Figure 10 presents the instantaneous positions of the interface under the influence of subcooling for different Stefan number. One can see that the degree of the phase change process is strongly dependent on the degree of subcooling. With the increase of the degree of subcooling applied to the melting process, the melting rate decreases and the propagation speed of the interface decelerates since the start of the melting process. Also, the larger the degree of subcooling is, the more retarded the melting process becomes. The reason for the existence of subcooling is that the initial temperature (T_i) of the solid PCM was set to be lower than its melting temperature (T_m). Therefore, the solid PCM absorbs heat and increases its sensible energy in terms of temperature rise after the boundary’s temperature was sharply increased to T₀, and the phase change won’t start until the entire solid reached its melting temperature (T_m). As a result, the moving curves exhibited “delayed” melting process compared to the base case without subcooling (Sc=0). Also, from Figure 10, one can see that the propagation behavior of the interface is quite different from that for different Stefan number, which means that the melting process as well as the predicted values of thermal conductivity is also dependent on Stefan number. Furthermore, the moving speed of the interface for larger Stefan number is faster than that of the smaller ones, and the interface moves faster at the beginning and slows down as the melting further proceeds for all the cases. The non-linear trend of the interfaces’ curve is induced by the constant boundary temperature required by the Stefan melting model. In effect, according to Stefan melting model, the temperatures of the thermal boundary and the interface were fixed at T₀ and T_m, respectively, which means the temperature drop over the liquid region was also fixed. As the melting further proceeds, the span of the liquid region increased, leading to a deceasing temperature gradient over the entire liquid region. The heat flux penetrated into the interface was decreased with the decreasing of the temperature gradient at the interface, and therefore the propagation rate of the interface is decreased.

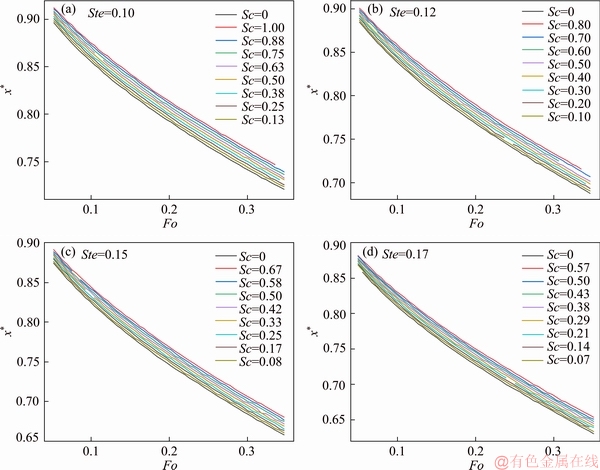
Figure 10 Interface’s moving curves versus melting time subject to different degree of subcooling ranging from 0 to 1 for different Stefan number

Variations of the predicted thermal conductivity against melting time are given in Figure 11. Examination of the predicted thermal conductivity in Figure 11 clearly points out that the values of the thermal conductivity obtained under the effect of subcooling are all smaller than the reference value. The effect of subcooling altered the moving feature of interface, by decreasing its propagation rate since the very beginning of the melting. Consequently, the position of the interface was comparatively overestimated, and therefore, the obtained values of thermal conductivity were comparatively smaller than the literature value. Also, the predicted values of k show a strong dependence on the degree of the subcooling; the larger the degree of subcooling is, the smaller the value obtained is. For example, when Ste=0.12, Fo=0.075, the predicted value is about 0.95 for Sc=0.1, while the predicted value is about 0.73 for Sc=0.8.

The numerically determined data of the thermal conductivity over the entire time span of the melting were presented in terms of Stefan number, Fourier number and degree of subcooling. The data were extracted from the 36 numerical cases and were found to be well correlated in the following dimensionless form:

k^′/k=(1.142Fo^-0.0169Ste^0.076+0.4573Fo^-0.4265Ste^0.5931Sc^1.097)           (17)

The dependency of the proposed correlation on the degree of subcooling is found to be dominant. The calibrated values of thermal conductivity through Eq. (16) are displayed in Figure 12. We can see that the empirical correlation mitigates the impact of the model simplification, by limiting the measurement error within the rage of ±3%. The valid range of for the proposed correlation is 0.1≤Ste≤0.2, 0≤Sc≤0.0.1 and 0≤Fo≤0.35.

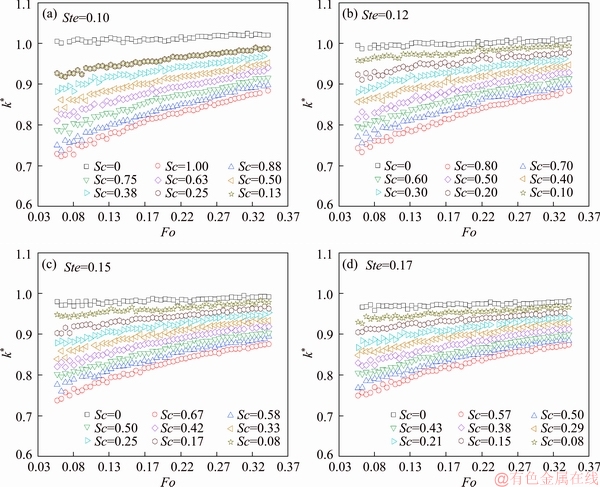
Figure 11 Predicted thermal conductivity versus melting time subject to different degrees of subcooling ranging from 0 to 1 for different Stefan number

Figure 12 Calibrated thermal conductivity versus melting time subject to different degrees of subcooling ranging from 0 to 1 for different Stefan number

4.5 Effect of natural convection on predicted thermal conductivity

The dependences of the interface’s moving behavior and the thermal conductivity on the effect of natural convection are investigated numerically. The transient positions of the interface are presented against the melting time for different Rayleigh number Ra in Figure 13.

                      (18)

where α and υ represent the thermal diffusivity and the kinematic viscosity of the liquid PCM, respectively. Because conduction and natural convection will both affect the temperature distribution in the liquid area and affect the behaviour of the melting process, the SteFo number was assumed to be the appropriate time scale. Also, in Figure 13, the case for Ra=0 denotes to the pure conduction melting process. This figure clearly shows the effect of natural convection on the melting process in terms of the moving feature of the interfaces. At the initial stage of melting, for time instance 0≤SteFo≤0.003, the melting behavior of the PCM for different Ra number is almost the same as that of the pure conduction. This is because the molten PCM layer thickness is very small at the beginning of the test, conduction is likely to be the dominant heat transfer mechanism. As the melting progresses, when SteFo≥0.003, the molten layer expands to a certain extent, the intensity of natural convection starts to increase, creating flow circulation that occupies the entire liquid region. Consequently, the heat transfer rate is augmented, thereby accelerating the moving speed of the interface.

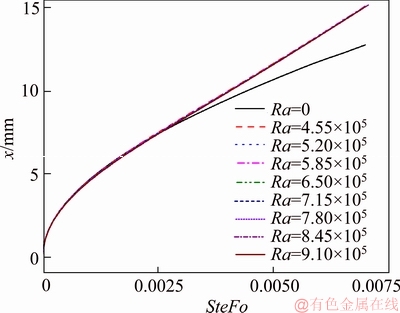
Figure 13 Interface’s moving trajectory versus melting time subject to different degree of natural convection

Another feature of Figure 13 is that the displacement curves of the interface for different Rayleigh number overlap with each other during the melting process, suggesting that the degree of the natural convection has little effect on the melting process. Thus, the data in Figure 13 are plotted in Figure 14 with the displacement differences of the interface between the natural convection affected cases and pure conduction case as the abscissa. Figure 14 shows that the deviation has a strong dependence on Ra number, the larger the Ra number is, the faster the interface moves. When SteFo=0.006, the increase of the interface’s position is about 2 mm compared to the pure conduction case, and the corresponding relative deviation is about 10%.

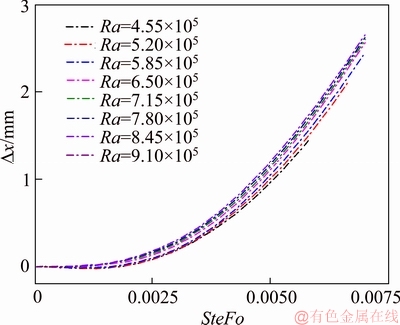
Figure 14 Deviation of interface’s moving trajectory between natural convection affected cases and pure conduction case for different degree of natural convection

Variations of the predicted thermal conductivity subjected to different degree of natural convection against heating time are given in Figure 15. As expected, the values of thermal conductivity are overestimated since the very beginning of the test due to the onset of natural convection. As the melting progresses, the measurement results display a monotonic increasing trend compared to the reference value. Again, the regression analysis was used to develop a correlation. The simulation data for the melting process are presented in terms of Fo, Ra, and are found to be likely correlated by the following dimensionless form:

       (19)

The calibrated values of thermal conductivity by Eq. (18) are displayed in Figure 16. We can see that the empirical correlation mitigates the impact of the natural convection, by limiting the measurement error within the range of ±2%. Also, for mitigating the impact of the natural convection during the experiment, it is suggested that the sampling time should be around SteFo=0.003.

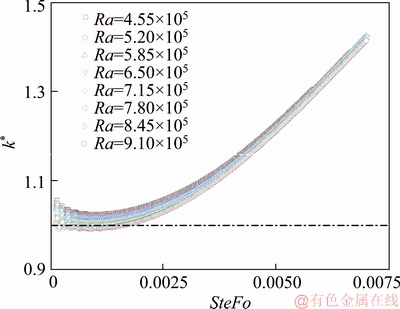
Figure 15 Predicted thermal conductivity subject to different degree of natural convection

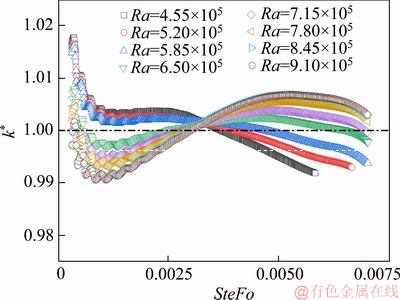
Figure 16 Calibrated thermal conductivity subject to different degrees of natural convection

5 Conclusions

This paper explores impact factor analysis for the measurement issues associated with the interface propagation-based thermal conductivity method. A 3-D transient heat transfer problem combined with solid-liquid phase change was established and solved with the aid of the numerical technique. The influencing factors, namely model simplification, subcooling and natural convection, along with their impact on thermal conductivity measurements were systematically investigated in terms of interface’s moving characteristics and corresponding predicted values of thermal conductivity.

The influence of simplified model shows a strong dependence on Stefan number of the melting process, and the predictions on the thermal conductivity present a monotonic increasing trend as the Stefan number increases. The degree of subcooling would lead to underestimated thermal conductivity prediction, the larger the degree of subcooling is, the smaller the value of thermal conductivity is estimated. The effect of natural convection would intensify the heat transfer rate near the interface, and the predicted thermal conductivity is overestimated as the melting progresses. Through regression analysis, correlations are provided to quantitatively describe the impact of the influencing factors on the measurement results, and the operation guidelines for mitigating the measurement errors are also provided. The relative measurement errors are limited in ±1.5%, ±3% and ±2% corresponding to the impact of simplified model, subcooling and natural convection, respectively.

The underlying mechanism casing measurement error for wider range of experimental conditions, i.e. bigger Stefan number, longer melting time, has not been studied in the present study. Hence, deep going investigation needs to be carried out for wider range of experimental conditions, which requires larger number of time frames. This issue, therefore, will be our next focus.

Nomenclature

c_p

Specific heat capacity, J/(kg·K)

Fo

Fourier number

H

Height of the cylinder, mm

J₀

Zero-order Bessel function of the first kind

J₁

First-order Bessel function of the first kind

k

Thermal conductivity, W/(m·K)

L

Latent heat, J/kg

n

Number of summation

R

Radius of the cylinder, mm

r

Radial coordinate, mm

S

Source term

Sc

Degree of subcooling

Ste

Stefan number

T

Temperature, K

T₀

Final boundary temperature, K

T_i

Initial temperature of solid PCM, K

T_m

Melting temperature of PCM, K

u

Velocity, m/s

x

Location of interface, mm

Greek symbols

α

Thermal diffusivity, m²/s

β

Liquid fraction

γ

Thermal expansion coefficient, 1/K

μ

Dynamic viscosity, kg/(m·s)

ρ

Density, kg/m³

τ

Time, s

υ

Kinematic viscosity, m²/s

Superscripts

-

Dimensionless

Subscripts

cal

Calculated values from experimental results

i,j

Dimension vectors

num

Numerically obtained results

ref

Reference

References

[1] MOHAMED S A, Al-SULAIMAN F A, IBRAHIM N I. A review on current status and challenges of inorganic phase change materials for thermal energy storage systems [J]. Renewable and Sustainable Energy Reviews, 2017, 70(4): 1072-1089. DOI: 10.1016/j.rser.2016.12.012.

[2] QURESHI Z A, ALI H M, KHUSHNOOD S. Recent advances on thermal conductivity enhancement of phase change materials for energy storage system: A review [J]. International Journal of Heat and Mass Transfer, 2018, 127: 838-856. DOI: 10.1016/j.ijheatmasstransfer.2018.08.049.

[3] RAO Zhong-hao, XU Tao-tao, LIU Chen-zhen, ZHENG Zhang-jing, LIANG Lin, HONG Kun. Experimental study on thermal properties and thermal performance of eutectic hydrated salts/expanded Perlite form-stable phase change materials for passive solar energy utilization [J]. Solar Energy Materials and Solar Cells, 2018, 188: 6-17. DOI: 10.1016/j.solmat.2018.08.012.

[4] WAHID M A, HOSSEINI S E, HUSSEN H M, AKEIBER H J, SAUD S N, MOHAMMAD A T. An overview of phase change materials for construction architecture thermal management in hot and dry climate region [J]. Applied Thermal Engineering, 2017, 112: 1240-1259. DOI: 10.1016/ j.applthermaleng.2016.07.032.

[5] KENISARIN M M. High-temperature phase change materials for thermal energy storage [J]. Renewable and Sustainable Energy Reviews, 2015, 14(3): 955-970. DOI: 10.1016/j.rser.2009.11.011.

[6] AGYENIM F, HEWITT N, EAMES P, SMYTH M. A review of materials, heat transfer and phase change problem formulation for latent heat thermal energy storage systems (LHTESS) [J]. Renewable and Sustainable Energy Reviews, 2010, 14(2): 615-628. DOI: 10.1016/j.rser.2009.10.015.

[7] WEN Rui-long, JIA Pu-qi, HUANG Zhao-hui, FANG Ming-hao, LIU Yan-gai, WU Xiao-wen, MIN Xin. Thermal energy storage properties and thermal reliability of PEG/bone char composite as a form-stable phase change material [J]. Journal of Thermal Analysis and Calorimetry, 2018, 132(3): 1753-1761.DOI:10.1007/s10973-017-6934-8.

[8] YANG Xiao-hu, LIU Jing. A novel method for determining the melting point, fusion latent heat, specific heat capacity and thermal conductivity of phase change materials [J]. International Journal of Heat and Mass Transfer, 2018, 127: 457-468. DOI: 10.1016/j.ijheatmasstransfer.2018.07.117.

[9] DIDIER G, MUSTAPHA K, ALMAADEED M A, KTUPA I. A new experimental device and inverse method to characterize thermal properties of composite phase change materials [J]. Composite Structures, 2015, 133: 1149-1159. DOI:10.1016/j.compstruct.2015.08.032.

[10] RICKLEFS A. Thermal conductivity of cementitious composites containing microencapsulated phase change materials [J]. International Journal of Heat and Mass Transfer, 2017, 104: 71-82. DOI: 10.1016/j.ijheatmasstransfer.2016. 08.013.

[11] GUNASEKARA S N, IGNATOWICZ M, CHIU J N. Thermal conductivity measurement of erythritol, xylitol, and their blends for phase change material design: A methodological study [J]. International Journal of Energy Research, 2019, 43: 1785-1801. DOI:10.1002/er.4403.

[12] WANG Ting-yu, WANG Shuang-feng, WU Wei. Experimental study on effective thermal conductivity of microcapsules based phase change composites [J]. International Journal of Heat and Mass Transfer, 2017, 109: 930-937. DOI: 10.1016/ j.ijheatmasstransfer.2017.02.068.

[13] GHOSSEIN R M A, HOSSAIN M S, KHODADADI J M. Experimental determination of temperature-dependent thermal conductivity of solid eicosane-based silver nanostructure-enhanced phase change materials for thermal energy storage [J]. International Journal of Heat and Mass Transfer, 2017, 107: 697-711. DOI: 10.1016/ j.ijheatmasstransfer.2016.11.059.

[14] HARISH S, OREJON D, TAKATA Y, KOHNO M. Thermal conductivity enhancement of lauric acid phase change nanocomposite with graphene nanoplatelets [J]. Applied Thermal Engineering, 2015, 80: 205-211. DOI: 10.1016/j.applthermaleng.2015.01.056.

[15] PALACIOS A, CONG L, NAVARRO M E, DING Y, BARRENECHE C. Thermal conductivity measurement techniques for characterizing thermal energy storage materials-A review [J]. Renewable and Sustainable Energy Reviews, 2019, 108: 32-52. DOI: 10.1016/j.rser.2019. 03.020.

[16] HARISH S, OREJON D, TAKATA Y, KOHNO M. Thermal conductivity enhancement of lauric acid phase change nanocomposite with graphene nanoplatelets [J]. Applied Thermal Engineering, 2015, 80: 205-211. DOI: 10.1016/ j.applthermaleng.2015.01.056.

[17] XUAN Yi-min, HUANG Yong, LI Qiang. Experimental investigation on thermal conductivity and specific heat capacity of magnetic microencapsulated phase change material suspension [J]. Chemical Physics Letters, 2009, 479(4-6): 264-269. DOI: 10.1016/j.cplett.2009.08.033.

[18] NABIL M, KHODADADI J M. Computational/ analytical study of the transient hot wire-based thermal conductivity measurements near phase transition [J]. International Journal of Heat and Mass Transfer, 2017, 111: 895-907. DOI: 10.1016/j.ijheatmasstransfer.2017.04.043.

[19] HOQUE M S B, ANSARI N, KHODADADI J M. Explaining the “anomalous” transient hot wire-based thermal conductivity measurements near solid-liquid phase change in terms of solid-solid transition [J]. International Journal of Heat and Mass Transfer, 2018, 125: 210-217. DOI: 10.1016/ j.ijheatmasstransfer.2018.04.014.

[20] CARSLAW H S, JAEGER J C. Conduction of heat in solids [M]. 2nd ed. London, UK: Oxford University Press, 1959.

[21] CABEZA L F, BARRENECHE C, MARTORELL I, SARIBEY L M S, FOIS M, PAKSOY H O, SAHAN N, WEBER R, CONSTANTINESCU M, ANGHEL E M, MALIKOVA M, KRUPA I, DELGDO M, DOLADO P, FURMANSKI P, JAWORSKI M, HAUSSMANN T, GSCHWANDER S, FERNANDEZ A I. Unconventional experimental technologies available for phase change materials (PCM) characterization. Part 1. Thermophysical properties [J]. Renewable and Sustainable Energy Reviews, 2015, 43: 1399-1414. DOI: 10.1016/j.rser.2014.07. 191.

[22] ZHANG Yin-ping, JIANG Yi, JIANG Yi. A simple method, the -history method, of determining the heat of fusion, specific heat and thermal conductivity of phase-change materials [J]. Measurement Science and Technology, 1999, 10(3): 201-205. DOI: 10.1088/0957-0233/10/3/015.

[23] ZHANG P, MA Z W, SHI X J, XIAO X. Thermal conductivity measurements of a phase change material slurry under the influence of phase change [J]. International Journal of Thermal Sciences, 2014, 78: 56-64. DOI: 10.1016/ j.ijthermalsci.2013.11.013.

[24] O’CONNOR W E, WARZOHA R, WEIGAND R, FLEISCHER A S, WEMHOFF A P. Thermal property prediction and measurement of organic phase change materials in the liquid phase near the melting point [J]. Applied Energy, 2014, 132: 496-506. DOI: 10.1016/ j.apenergy.2014.07.045.

[25] ZHOU Tian, LIU Xu, LI Yuan, SUN Zhi-qiang, ZHOU Jie-min. Dynamic measurement of the thermal conductivity of phase change materials in the liquid phase near the melting point [J]. International Journal of Heat and Mass Transfer, 2017: 631-641. DOI: 10.1016/j.ijheatmasstransfer. 2017.04.020.

[26] ZALBA B, MARIN J M, CABEZA L F, MEHLING H. Review on thermal energy storage with phase change: Materials, heat transfer analysis and applications [J]. Applied Thermal Engineering, 2003, 23(3): 251-283. DOI: 10.1016/ s1359-4311(02)00192-8.

[27] MARCUS Y. Heat capacities of molten salts with polyatomic anions [J]. Thermochimica Acta, 2009, 495(1): 81-84. DOI: 10.1016/j.tca.2009.06.003.

[28] ASSIS E, KATSMAN L, ZISKIND G, LETAN R. Numerical and experimental study of melting in a spherical shell [J]. International Journal of Heat and Mass Transfer, 2007, 50(9, 10): 1790-1804. DOI: 10.1016/j.ijheatmasstransfer.2006.10. 007.

(Edited by YANG Hua)

中文导读

界面移动法测量相变材料热导率影响因素的定量研究

摘要：相比传统测量方法，界面移动法对处于相变过程中相变材料热导率的测量有着明显的优势。但在前期研究中，研究者仅对界面移动法中引入测量误差的综合效应进行了定性描述，缺乏对各影响因素的深入分析。本文用数值模拟，对界面移动法中引入测试误差的三种因素(模型简化、次冷效应和自然对流)进行定量分析，并探讨这些因素对测量过程以及测量结果的影响机制。数值结果表明，模型简化对测量结果的影响取决于斯蒂芬数的大小；次冷效应的存在会导致测量结果偏小；自然对流将强化界面处的传热强度，从而导致测量结果偏大。本文对实验操作过程提出了改进方法，并拟合得到修正关系式以减小测量误差。针对模型简化、次冷效应和自然对流三种影响因素，其修正后的测量结果相对误差分别在±1.5%，±3%和 ±2%范围内。

关键词：相变材料；热导率测量；界面移动法；影响因素；界面移动法；数值计算

Foundation item: Project(51606224) supported by the National Natural Science Foundation of China

Received date: 2019-05-30; Accepted date: 2019-07-05

Corresponding author: LI Yuan, PhD, Lecturer; Tel: +86-731-88879863; E-mail: 214080@csu.edu.cn; ORCID: 0000-0003-0503-2178