基于滑模观测器的交流伺服系统
摩擦力矩自适应补偿控制
张文静,徐洪泽
(北京交通大学 电子信息工程学院,北京,100044)
摘要:针对高精度交流伺服系统中存在的非线性动态摩擦,提出一种基于LuGre摩擦模型的滑模自适应补偿控制方法,该方法利用滑模观测器解决了LuGre摩擦模型中状态变量未知且不可测的问题,在此基础上设计包含PD控制和自适应控制的控制器,给出参数的自适应律,利用Lyapunov方法证明了控制系统的全局渐进稳定性。仿真结果表明:基于滑模观测器的自适应补偿控制能实现对低速期望轨迹的跟踪,并能提高伺服系统的跟踪精度。
关键词:交流伺服系统;摩擦补偿;滑模观测器;自适应控制
中图分类号:TP273 文献标志码:A 文章编号:1672-7207(2011)S1-0299-05
An adaptive friction compensation control for PMSM servo system based on sliding mode observer
ZHANG Wen-jing, XU Hong-ze
(School of Electronic and Information Engineering, Beijing Jiaotong University, Beijing 100044, China)
Abstract: To a high performance AC servo system with nonlinear friction, based on LuGre friction model, an adaptive control method was proposed. To estimate parameters in LuGre friction model, a sliding mode observer was presented. Furthermore, a controller including PD component and adaptive component was developed, adaptive laws were given, and asymptotic stability was theoretically guaranteed by using Lyapunov stability theorem. Simulation results well verify the effectiveness of the proposed scheme for low speed motion trajectory tracking and the tracking performance is improved.
Key words: AC servo system; friction compensation; sliding mode observer; adaptive control
在高精度交流伺服控制系统中,非线性摩擦对系统的动态及静态性能的影响很大,主要表现为:低速时的爬行现象、速度过零时的波形畸变现象、稳态时有较大的静差,甚至出现极限环振荡[1]。为了提高伺服系统的位置控制精度和改善系统的低速性能, 需要对系统摩擦力矩进行补偿, 从而使系统性能更优良。目前,应用于高精度伺服控制系统的摩擦模型较多,因为任务及模型各不相同,相应的补偿方法多种多样。实践表明,采用经典的库仑摩擦+黏性摩擦模型并不能真实地反映摩擦现象的动态过程。因此,基于经典摩擦模型的补偿控制难以取得令人满意的效果。LuGre摩擦模型[2]是一个较为完善的动态摩擦模型,该模型考虑了2个接触表面之间弹性鬃毛的平均形 变来表征摩擦的动态行为,精确地描述了摩擦过程复杂的静态和动态特性,如爬行、极限环振荡、滑前变形、摩擦记忆、变静摩擦以及静态Stribeck曲线等。滑模自适应控制是滑模变结构控制与自适应控制的有机结合,是解决参数不确定或时变参数系统控制问题的一种新型控制策略。近年来,滑模自适应控制理论取了一系列重要进展,在摩擦补偿方面得到了很好的应用[3-5]。在此,本文作者分析了交流伺服系统的摩擦力矩,基于LuGre摩擦模型,提出了一种新的自适应补偿控制算法,实现了摩擦力矩的动态补偿控制,利用Lyapunov直接法证明了控制系统的全局渐进稳定性,并给出了仿真结果。
1 系统模型简介
考虑非线性摩擦力矩,可以得到如下的简化控制系统动态方程:
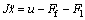 (1)
(1)
其中:J为折合到电机轴的转动惯量;u为控制力矩;Ff为摩擦力矩;Fl为负载扰动力矩。
设状态变量z表示接触面鬃毛的平均形变,则LuGre摩擦模型的数学表达式为:
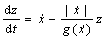 (2)
(2)
 (3)
(3)
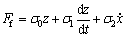 (4)
(4)
其中: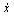 为瞬时角速度;Fc为库仑摩擦力矩;Fs为静摩擦力矩;σ2为黏性摩擦因数;
为瞬时角速度;Fc为库仑摩擦力矩;Fs为静摩擦力矩;σ2为黏性摩擦因数;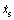 为临界Stribeck 速度;σ0为刚度系数;σ1为黏性阻尼系数。
为临界Stribeck 速度;σ0为刚度系数;σ1为黏性阻尼系数。
在式(4)中,令dz/dt=0,即可得到稳态时摩擦力矩与转速之间的关系
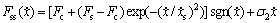 (5)
(5)
式(5)所确定的转速与摩擦力矩曲线称为Stribeck曲线。
2 基于滑模观测器的自适应控制器设计
2.1 控制器设计
首先定义如下的交流伺服系统跟踪误差:
e=xd-x (6)
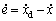 (7)
(7)
其中:xd为期望跟踪信号连续且二阶可导,另外,xd,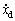 和
和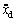 均有界。
均有界。
定义滑模面为:
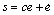 (8)
(8)
其中:c为正的设计常数。另一个误差函数s?(t)定义为[6]:
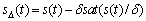 (9)
(9)
其中:sat(?)为一个饱和函数,定义为
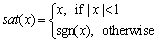 (10)
(10)
因此,控制器的设计问题变为设计一个自适应控制律u(t),使得能够保证跟踪误差s在所有的t>0时刻位于预设的δ界内。
将式(3)~(5) 代入式(1)中,可得
 -Fi (11)
-Fi (11)
其中:σ=σ1+σ2>0; 。因为
。因为 为严格正实且有界的,所以,
为严格正实且有界的,所以,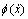 也是严格正实且有界的。因此,不失一般性,可以假定
也是严格正实且有界的。因此,不失一般性,可以假定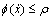 ,其中ρ为一个正的常数。
,其中ρ为一个正的常数。
在式(11)中,由于参数J, σ,σ0,σ1和Fi均未知, 本文利用其估计值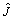 ,
, 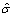 ,
,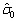 ,
,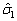 和
和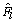 来代替。
来代替。
LuGre摩擦模型中的状态变量z是未知且不可测的。本文采用下面的观测器来估计z,观测器方程为:
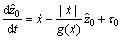 (12)
(12)
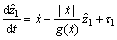 (13)
(13)
其中: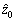 和
和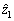 为摩擦状态变量z的估计值;τ0和τ1为需要设计的观测器动态项。误差估计如下:
为摩擦状态变量z的估计值;τ0和τ1为需要设计的观测器动态项。误差估计如下:
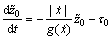 (14)
(14)
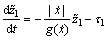 (15)
(15)
其中: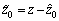 ;
;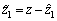 。
。
对式(8)求导,并将式(11)代入,可得:
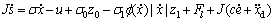 (16)
(16)
对于非线性伺服控制系统(1),构造如下的非线性控制器:
u=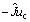
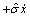 +
+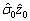
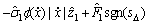 (17)
(17)
其中:uc是一个辅助的控制项,定义如下:
 (18)
(18)
将式(17)和(18)代入式(16),可得:
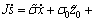
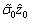
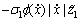
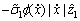 +
+
 (19)
(19)
进而,
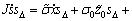
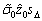
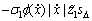 -
-
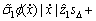
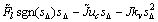 (20)
(20)
下面给出各未知参数和摩擦状态观测器动态项的自适应律。
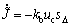 (21)
(21)
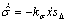 (22)
(22)
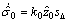 (23)
(23)
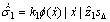 (24)
(24)

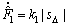 (25)
(25)
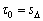 (26)
(26)
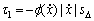 (27)
(27)
其中:kJ, kσ, k0, k1和 kl均为正的设计常数。
2.2 稳定性定理
定理:给定控制系统(1),定义式(8)所示的滑模面,采用式(17)和(18)组成的控制器,选用式(21)~(27)所示的自适应律,则控制系统在Lyapunov意义下是渐进稳定的,当 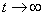 时,位置跟踪误差(式(6))收敛于0。
时,位置跟踪误差(式(6))收敛于0。
证明: 首先定义未知参数的估计误差:
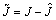 ,
,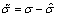 ,
,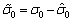 ,
,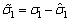 ,
,
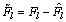 。
。
选择如下的Lyapunov函数:
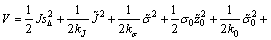
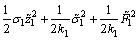 (28)
(28)
对式(28)求导,可得:
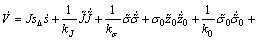
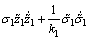 +
+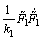 (29)
(29)
将式(6)~(8)以及(14)~(18)代入式(29),可得:
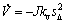
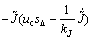 +
+
 -
-
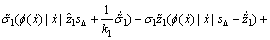
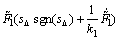 (30)
(30)
由式(14)和(15)可得:
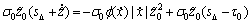 (31)
(31)
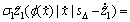
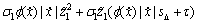 (32)
(32)
将式(31)和(32)及上面定义的估计误差代入式(29)可得:
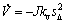
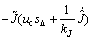
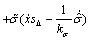 +
+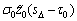
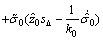 -
-
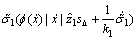
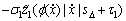 +
+
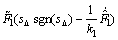 -
-
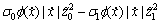 (33)
(33)
将式(21)~(27)所定义的自适应控制律代入式(33)可得:
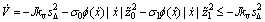 (34)
(34)
由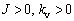 可得:当
可得:当 时,
时,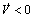 ,是负定的,所以,控制系统在Lyapunov稳定意义下是稳定的,且对任意初始条件J,σ,σ0,σ1,Fl和V都是有界的。由于函数V>0且有下界,且为非增函数,可得:
,是负定的,所以,控制系统在Lyapunov稳定意义下是稳定的,且对任意初始条件J,σ,σ0,σ1,Fl和V都是有界的。由于函数V>0且有下界,且为非增函数,可得:
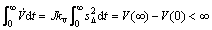 (35)
(35)
因为s?有界,由式(6)和(7)可得,e和 均有界,根据式(18)可得控制量uc是有界的,进而根据式(17)可知:系统的实际控制量u是有界的。根据式(16)可知:
均有界,根据式(18)可得控制量uc是有界的,进而根据式(17)可知:系统的实际控制量u是有界的。根据式(16)可知: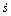 是有界的,进而
是有界的,进而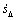 是有界的。由Barbalat定理可知,当
是有界的。由Barbalat定理可知,当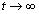 时,s?趋于0,跟踪误差收敛至0。
时,s?趋于0,跟踪误差收敛至0。
证毕。
补充说明:
(1) 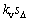 实际上就是传统的PD控制器,因此,c和kv的初始值设置可以使用目前很多成熟的PD控制器的设计方法;
实际上就是传统的PD控制器,因此,c和kv的初始值设置可以使用目前很多成熟的PD控制器的设计方法;
(2) 在设计滑模自适应控制器时,为了提高跟踪精度,选取的δ要求尽可能小。然而,很小的δ有可能引起控制器输出的高度不连续性,而且有可能在控制器输入端引起抖振。因此,必须在跟踪精度和控制器输出的不连续性2个方面进行折中处理。
3 仿真研究
本节考察对存在非线性摩擦力矩干扰的PMSM交流伺服系统,采用摩擦补偿前后的系统速度及位置跟踪性能。电机参数为: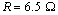 ,
,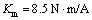 ,Ce=1.1 V/(rad·s-1),J=1.0 kg·m2,KPWM=50 V/V。LuGre摩擦模型参数为:Fc=20,Fs=25,
,Ce=1.1 V/(rad·s-1),J=1.0 kg·m2,KPWM=50 V/V。LuGre摩擦模型参数为:Fc=20,Fs=25,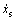 =0.01,σ2=0.02,σ0=500,σ1=2.5。低速给定正弦指令为
=0.01,σ2=0.02,σ0=500,σ1=2.5。低速给定正弦指令为
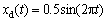 (36)
(36)
采用PD控制,控制器为:
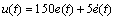 (37)
(37)
位置和速度跟踪结果如图1和2所示。仿真结果表明:当伺服系统存在非线性摩擦时,位置跟踪存在“平顶”现象,速度跟踪存在“死区”现象。采用PD控制鲁棒性差,无法实现高精度跟踪。
采用本文提出的滑模自适应补偿控制器,控制参数取c=50,δ=80,位置跟踪和速度跟踪结果如图3和4所示,摩擦力Stribeck曲线如图5所示,控制器的输出控制力矩如图6所示,滑模运动的相轨迹如图7所示。
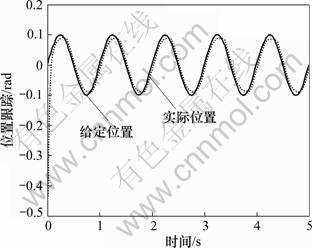
图1 PD控制的位置跟踪曲线
Fig.1 Position trajectory of PD control
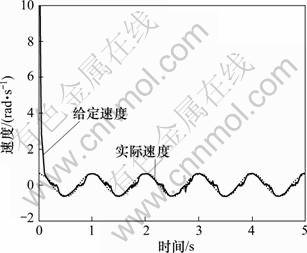
图2 PD控制的速度跟踪曲线
Fig. 2 Velocity trajectory of PD control
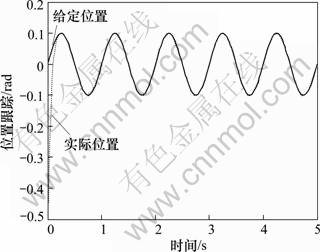
图3 滑模自适应控制的位置跟踪曲线
Fig. 3 Position trajectory of adaptive sliding mode control
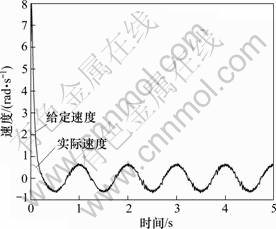
图4 滑模自适应控制的速度跟踪曲线
Fig.4 Velocity trajectory of adaptive sliding mode control
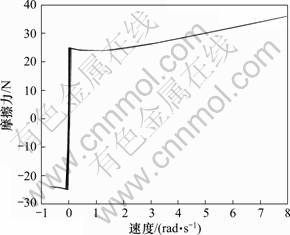
图5 Stribeck曲线
Fig.5 Stribeck curve
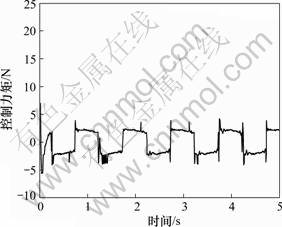
图6 控制力矩的变化曲线
Fig.6 Curve of control input
从仿真结果可以看出:利用滑模自适应补偿控制器可以有效地抑制系统中的非线性摩擦影响,提高了系统的低速运行性能。
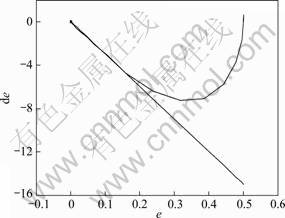
图7 相轨迹
Fig.7 Phase trajectory
4 结论
(1) 针对交流伺服系统运行过程中模型参数的变化,本文应用2个非线性观测器在线估计LuGre模型中的未知摩擦状态,提出了一种基于LuGre摩擦模型的滑模自适应补偿方法。该方法控制器包含一个等效PD控制律和一个参数自适应律,实现了对未知LuGre模型参数和负载力矩参数的估计,利用Lyapunov方法证明了系统的全局稳定性。
(2) 基于LuGre摩擦模型的滑模自适应补偿可以有效地抑制非线性摩擦对伺服系统速度输出造成的影响,克服了系统爬行现象,提高了系统的低速平稳性和跟踪精度。这种补偿方法对类似的存在摩擦干扰的控制系统同样适用,因而有着广阔的应用价值。
参考文献:
[1] Armstrong B, Dupont P, de Wit C C. A survey of models, analysis tools and compensation methods for the control of machines with friction [J]. Automatic, 1994, 30(7): 1083-1138.
[2] de Wit C C, Olsson H, Astrom K J, et al. A new model for control of systems with friction [J]. IEEE Transaction on Automation Control, 1995, 40(3): 419-425.
[3] XIE Wen-fang. Sliding-mode-observer-based adaptive control for servo actuator with friction [J]. IEEE Transaction on Industrial Electronics, 2007, 54(3): 1517-1527.
[4] ZENG Hai-rong, Sepehri R. Adaptive backstepping control of hydraulic manipulators with friction compensation using LuGre model [C]//Proceedings of the 2006 American Control Conference. Minneapolis, 2006: 164-3169.
[5] Han S I, Cho Y S, Jin S M, et al. Adaptive friction observer and sliding mode controller development with RFNN for nonlinear friction compensation [C]//Proceedings of 2009 ICROS-SICE International Joint Conference. Fukuoka, Japan, 2009: 4971-4976.
[6] Slotine J J E, Coetsee J A. Adaptive sliding controller synthesis for nonlinear system[J]. Int J Control, 1986, 43(6): 1631-1651.
(编辑 杨幼平)
收稿日期:2011-04-15;修回日期:2011-06-15
基金项目:国家科技支撑计划项目(2011BAG01B03)
通信作者:张文静(1976-),男,甘肃定西人,博士后,讲师,从事交流伺服控制研究;电话:13691550569;E-mail: zhangwj@bjtu.edu.cn