Robust model predictive control with randomly occurred networked packet loss in industrial cyber physical systems
来源期刊:中南大学学报(英文版)2019年第7期
论文作者:蔡宏斌 李平 SU Cheng-li苏成利 曹江涛
文章页码:1921 - 1933
Key words:robust model predictive control; networked control system; packet loss; linear matrix inequalities (LMIs)
Abstract: For a class of linear discrete-time systems that is subject to randomly occurred networked packet loss in industrial cyber physical systems, a novel robust model predictive control method with active compensation mechanism was proposed. The probability distribution of packet loss is described as the Bernoulli distributed white sequences. By using the Lyapunov stability theory, the existing sufficient conditions of the controller are derived from solving a group of linear matrix inequalities. Moreover, dropout-rate with uncertainty and unknown dropout-rate are also considered, which can greatly reduce the conservativeness of the controller. The designed robust model predictive control method not only efficiently eliminates the negative effects of the networked data loss in industrial cyber physical systems but also ensures the stability of closed-loop system. Two examples were provided to illustrate the superiority and effectiveness of the proposed method.
Cite this article as: CAI Hong-bin, LI Ping, SU Cheng-li, CAO Jiang-tao. Robust model predictive control with randomly occurred networked packet loss in industrial cyber physical systems [J]. Journal of Central South University, 2019, 26(7): 1921-1933. DOI: https://doi.org/10.1007/s11771-019-4121-8.

J. Cent. South Univ. (2019) 26: 1921-1933
DOI: https://doi.org/10.1007/s11771-019-4121-8
CAI Hong-bin(蔡宏斌)1, LI Ping(李平)2, SU Cheng-li(苏成利)2, CAO Jiang-tao(曹江涛)2
1. School of Automation, Northwestern Polytechnical University, Xi'an 710072, China;
2. School of Information and Control Engineering, Liaoning Shihua University, Fushun 113001, China
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019
Abstract: For a class of linear discrete-time systems that is subject to randomly occurred networked packet loss in industrial cyber physical systems, a novel robust model predictive control method with active compensation mechanism was proposed. The probability distribution of packet loss is described as the Bernoulli distributed white sequences. By using the Lyapunov stability theory, the existing sufficient conditions of the controller are derived from solving a group of linear matrix inequalities. Moreover, dropout-rate with uncertainty and unknown dropout-rate are also considered, which can greatly reduce the conservativeness of the controller. The designed robust model predictive control method not only efficiently eliminates the negative effects of the networked data loss in industrial cyber physical systems but also ensures the stability of closed-loop system. Two examples were provided to illustrate the superiority and effectiveness of the proposed method.
Key words: robust model predictive control; networked control system; packet loss; linear matrix inequalities (LMIs)
Cite this article as: CAI Hong-bin, LI Ping, SU Cheng-li, CAO Jiang-tao. Robust model predictive control with randomly occurred networked packet loss in industrial cyber physical systems [J]. Journal of Central South University, 2019, 26(7): 1921-1933. DOI: https://doi.org/10.1007/s11771-019-4121-8.
1 Introduction
Cyber physical systems (CPSs), a unity of computing process and the physical process, are the next generation intelligent system with integrating computing, communication and control [1]. CPS is a natural evolution resulted from the fast development of information and communication technology. The physical entity can be manipulated by the CPS with remote, reliable, secure and cooperative ways. In other words, complex physical processes are remotely controlled by cyber components [2, 3]. Nowadays, CPS has already been applied in more and more domains, such as smart grid [4], medical [5] and network security [6, 7]. Moreover, due to the urgent need of the industrial process, industrial cyber physical systems (ICPSs) have obtained a lot of attentions in recent years. Especially, the realization of industry 4.0 involves around the use of ICPSs [8].
Wireless network, which is the carrier of ICPSs, represents the interconnection of many production plants equipped with communication and sensing devices [9]. ICPSs rely on wireless network in order to interconnect sensors and actuators with performing measurement, supervision and protection functions in different domains. However, due to the limited bandwidth of wireless networks and other factors, network delay and packet loss are pervasive problems in ICPSs. Furthermore, packet loss is the most serious problem, which can lead to the instability of closed-loop system and cause other severe consequences, or, even worse [10]. Therefore, various approaches have been developed to deal with this issue, for instance, stochastic control approach [11], observer approach [12], switched system approach [13, 14], event-triggered approach [15, 16], iterative learning control approach [17].
Another effective approach to cope with the issue is model predictive control (MPC) method. MPC is a prevalent technique for slow dynamic systems, such as petrochemical process, medical [18, 19]. MPC is a model-based closed-loop optimization control scheme, which solves the optimization problem with control variables and state variables constraints [20-24]. However, uncertainties are unavoidable in the real world. In order to deal more effectively with these uncertainties, a robust model predictive control (RMPC) strategy was proposed [25, 26]. The RMPC takes advantage of the idea of robust control to cope with these uncertainties, and preserves the advantages of receding optimization of MPC. Moreover, RMPC on future control inputs can been effectively utilized to handle the influences of networked data loss. Therefore, it is significant to consider to design RMPC for dealing with the issue of packet loss in ICPSs.
During the past decades, the packet loss problem has obtained a lot of research results based on the MPC strategy. In Ref. [27], for the nonlinear system with networked environment randomly occurred both packet dropout and data quantization, the novel MPC method is investigated. SONG et al [28] proposed the distributed MPC algorithm for the uncertain nonlinear systems subject to randomly occurred networked packet loss and actuator saturation at the same time. Furthermore, SONG et al [29, 30] have also considered the networked packet loss under the different network protocol, RMPC and N-Step MPC have been researched to compensate the influence of packet loss, respectively. Moreover, for the both control signals and plant measurement signals subject to data loss and time-varying delays in the communication channels, the constrained MPC method is researched in the linear polytopic uncertain method framework [31]. In Ref. [32], for nonlinear systems with stochastic disturbances in the presence of data losses, the MPC method is researched to compensate the data loss in communication channel, which reduces the effect of packet loss for the stability of closed-loop system. PANG et al [33] have also studied the data-based networked predictive control approach in order to actively make up for the random round-trip time delay. It is worth mentioning that this method do not require any prior information on the system. Coincidentally, for nonlinear continuous-time systems, a new aperiodic formulation of MPC is proposed. Meanwhile, event-triggered conditions without using the optimal cost is treated as a Lyapunov candidate function [34]. Note that the model of data loss is also very important in order to effectively cope with data loss issue. On the one hand, for nonlinear systems that is subject to both packet dropout and data quantization, the novel MPC method has been already investigated. By designing networked data dropout compensation strategy and taking advantage of the Markov jump linear system model, the effects of data quantization and packet dropout are simultaneously compensated [35]. Similarly, TANG et al [36] have also researched that for nonlinear systems subject to parameter uncertainties, the synthesis approach of output feedback MPC has been proposed. The nonlinear system is represented by the interval type-2 Takagi–Sugeno fuzzy model. And the phenomenon of packet loss is described as a binary Markov chain. On the other hand, for the problem of networked packet loss under three different transmission protocols, a novel stochastic MPC has been proposed to keep the optimal performance. The packet loss was described as Bernoulli process, which was more approximately the real situation [37]. However, because of the wide application of CPS in industrial systems, the research on the issue of networked packet loss in ICPS is urgently necessary. In particular, how to apply the stochastic characteristics of data loss to achieve the desired performance of closed-loop system is still a challenged problem. At present, such research has not yet been seen.
In this work, the main contributions can be highlighted as follows: 1) For a class of linear discrete-time systems that is subject to randomly occurred packet loss in ICPSs, a novel RMPC method can be designed with active compensation mechanism in order to guarantee the optimal performance of system. 2) To better reflect packet loss phenomenon of the networked control system in the real world, dropout-rate with uncertainty and unknown dropout-rate have also been considered. Therefore, the discussed problems in this study are more general than most of those in existing literatures. 3) From the perspective of technology, the introduction of the dropout-rate with uncertainty and the unknown dropout-rate can bring the serious difficulty for designing controller, which are also the challenge and innovation of this study.
The rest of this paper is structured as follows: The mathematical formulation of data loss in ICPSs is presented in Section 2. Section 3 provides the sufficient conditions of the stochastic stability of closed-loop system. Section 4 illustrates the effectiveness of proposed control strategy by two examples. Section 5 draws a conclusion and discussion.
Notations: Rn denotes the n-dimensional Euclidean space.  refers to the system state measured at the sampling time k. AT denotes the transpose of matrix A.
refers to the system state measured at the sampling time k. AT denotes the transpose of matrix A.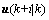 and
and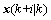 represent the future control input and predicted state at time k.
represent the future control input and predicted state at time k.  represents the Euclidean norm of the vector x. The symbol “*” refers to the symmetric part in the symmetric matrix. I denotes compatible dimensions identity matrix, respectively.
represents the Euclidean norm of the vector x. The symbol “*” refers to the symmetric part in the symmetric matrix. I denotes compatible dimensions identity matrix, respectively.
2 Problem formulation
A simple ICPS is shown in Figure 1. The communication infrastructures (network nodes), such as “sensor” nodes, “controller” nodes, and other intermediate nodes, are of vital importance for the ICPS, which depend on TCP/IP protocol to transmit information from sensors to controllers.
Consider a kind of discrete systems is described as
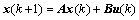 (1)
(1)
where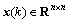 denotes the system state;
denotes the system state;  denotes the control input; matrices A and B are known system matrices of compatible dimension. Assume that the data loss may randomly occur between the sensor nodes and the controller nodes. For the sake of dealing with the bad effects caused by the packet loss, the state feedback control laws can be designed as follows:
denotes the control input; matrices A and B are known system matrices of compatible dimension. Assume that the data loss may randomly occur between the sensor nodes and the controller nodes. For the sake of dealing with the bad effects caused by the packet loss, the state feedback control laws can be designed as follows:
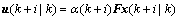 (2)
(2)
where F denotes the state feedback gain matrix; α(k) is the Bernoulli variable and considered to take values in a finite set Ω [0, 1]
[0, 1]
 (3)
(3)
In other words, when process data are sent from the sensor nodes to the controller nodes by wireless network in ICPS, it is assumed that the process of data loss can be described as the discrete-time Bernoulli distribution. One has
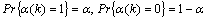 (4)
(4)
It can be verified that
 (5)
(5)
where E is expectation; α is the dropout-rate.
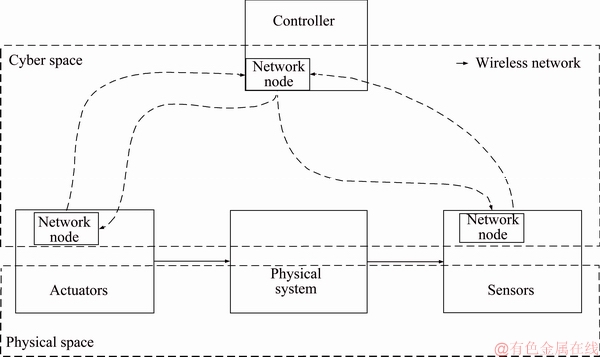
Figure 1 A simple industrial cyber physical system schematic
3 Robust model predictive controller design
Consider the following “min-max” performance cost:
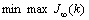
 (6)
(6)
where  and
and  are known positive definite symmetric state and input diagonal weighting matrices. Using the state feedback control laws (2), the closed-loop system can be derived as follows:
are known positive definite symmetric state and input diagonal weighting matrices. Using the state feedback control laws (2), the closed-loop system can be derived as follows:
 (7)
(7)
In order to simplify the following proof, Eq. (7) can be equivalent to

 (8)
(8)
As for Eq. (2), it can also be equivalent to
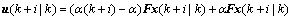 (9)
(9)
Remark 1: Due to the data loss occurrence in ICPSs, the closed-loop system may be suffered from severe performance deteriorations [10]. Therefore, the research on the effective method is necessary and urgent for dealing with networked data loss. In this work, the aim of the RMPC method is that when networked packet loss occurs, the system can be guaranteed to achieve the asymptotic stability of closed-loop system and the optimal performance.
The RMPC scheme is to design the state feedback control law (2), which is substituted into the optimization problem (6). At the current sampling time, the state feedback control gain matrix F is calculated by solving the optimization problem (6). And the first control input of the obtained control sequence is applied to the system. At the next sampling time, the “min-max” optimization problem (6) should be again solved with the updated state information to obtain a new control input.
Definition 1: The system (7) is achieved to be stochastically stable, and every initial condition 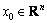 , if the following inequality holds
, if the following inequality holds

Let define the following quadratic function
 (10)
(10)
where P is positive definite symmetric matrix. Suppose that the quadratic function satisfies the following inequality at each sampling time k,
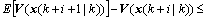
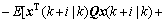
 (11)
(11)
As for inequality (11), both sides taking expectation and summing from 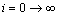
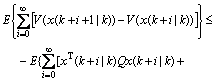
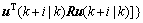 (12)
(12)
It can be written as follows:
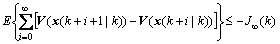 (13)
(13)
Assume that the closed-loop system is asymptotically stable. Thus, 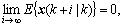 then,
then, 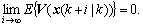 Furthermore, the upper bound of performance index can be obtained
Furthermore, the upper bound of performance index can be obtained
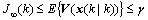 (14)
(14)
where γ is a positive scalar.
Theorem 1: Consider system (1) at each sampling time k. If positive symmetric matrices Q>0, R>0 are given, there are X>0, Y and scalar γ, satisfying
 (15)
(15)
subject to
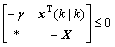 (16)
(16)
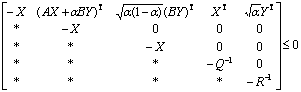 (17)
(17)
Then, the state feedback control gain matrix F can be directly obtained as follows:

Proof: According to inequality (14), by applying to Schur complement, inequality (16) can be obtained. As for inequality (11), it can be equal to the following inequality:


 (18)
(18)
For all 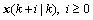 , inequality (18) can be satisfied. Therefore,
, inequality (18) can be satisfied. Therefore,
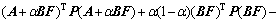
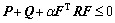 (19)
(19)
Pre-and post-multiply by X and its transpose, and define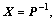
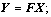 then if matrix inequality (17) holds, the condition (19) is satisfied.
then if matrix inequality (17) holds, the condition (19) is satisfied.
According to system (7), it is assumed that 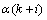 and
and 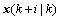 are mutually independent, then
are mutually independent, then
 (20)
(20)
It can be concluded that
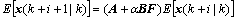 (21)
(21)
By defining 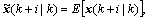 Eq. (21) can also be rewritten as follows:
Eq. (21) can also be rewritten as follows:
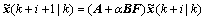 (22)
(22)
According to inequality (11), one can get
 (23)
(23)
Q and R are positive symmetric matrices, thus
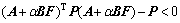 (24)
(24)
Then, we have
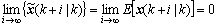 (25)
(25)
Moreover, the following inequality can be guaranteed.
 (26)
(26)
Therefore, the closed-loop system is stochastically asymptotically stable. The proof is completed.
According to Theorem 1, it can be seen that dropout-rate α plays a key role for the controller design subject to networked data loss, which should be exactly provided. However, in practice, the dropout-rate α is exactly obtained very difficult. Therefore, such general cases should be considered. In other words, if there exists uncertainty in α, it should use its estimation and describe it as
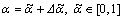 (27)
(27)
where is its estimation. And admissible uncertainties are
is its estimation. And admissible uncertainties are  and
and respectively. Then, the Theorem 2 can be concluded.
respectively. Then, the Theorem 2 can be concluded.
Theorem 2: Consider the system (1) at each sampling time k. Under condition (27), there exists the controller (2), then the closed-loop system (7) is stochastically stable. If positive symmetric matrices Q>0, R>0 are given, there are X>0, M>0, T>0, Y and scalars δ, γ, ε, satisfying
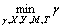 (28)
(28)
subject to
 (29)
(29)
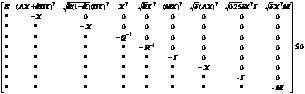 (30)
(30)
 (31)
(31)
 (32)
(32)
where 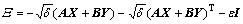 .
.
Proof: Similar to the proof of Theorem 1, according to inequality (19),

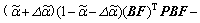
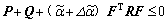 (33)
(33)
It is equivalent to
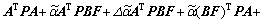
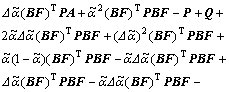
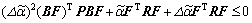 (34)
(34)
Inequlity (34) can also be rewritten as

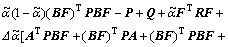
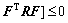 (35)
(35)
Then, it is not difficult to see that

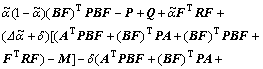
 (36)
(36)
Moreover, it is noted that for any T>0, one has
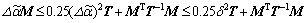 (37)
(37)
Under condition (27), substituting inequality (37) into inequality (36) yields


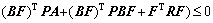 (38)
(38)
and
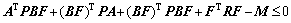 (39)
(39)
It is obvious that if conditions (38) and (39) hold, condition (36) can be guaranteed. As for condition (38),


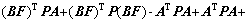
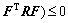 (40)
(40)
It can be equivalent to
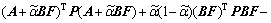
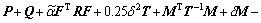
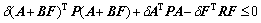 (41)
(41)
Pre-and post-multiply by X and its transpose, respectively, and define Y=FX, X=P-1. Furthermore, the following inequality can also be seen that


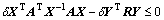 (42)
(42)
where
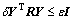 (43)
(43)
and it is got that

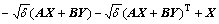 (44)
(44)
Applying to the Schur complement, the conditions (42) and (43) can be translated to the inequalities (30) and (32), respectively. As for condition (39), one can get

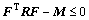 (45)
(45)
Therefore, it follows that
 (46)
(46)
Both sides multiply by X and its transpose, respectively. It is easy to conclude that
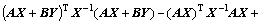
 (47)
(47)
As for nonlinear term  there is
there is
 (48)
(48)
Inequality (31) can be directly derived. The proof is completed.
It is very important to consider another general case that dropout-rate α is unknown, and to guarantee that the system (7) is stochastically stable. Similar to Theorem 2, the main result is derived as follows.
Theorem 3: Consider system (1) at each sampling time k. There is the controller (2), then the closed-loop system (7) is stochastically stable. If positive symmetric matrices Q>0, R>0 are given, there are X>0, Y and scalar γ, satisfying
Y and scalar γ, satisfying
 (49)
(49)
subject to
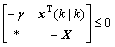 (50)
(50)
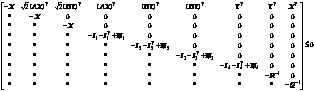 (51)
(51)
Proof: Similar to the proof of Theorem 1, according to condition (19)

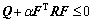 (52)
(52)
It is equivalent to
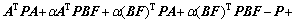
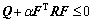 (53)
(53)
One can get
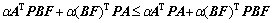 (54)
(54)
Then, inequality (53) can be expressed as
 (55)
(55)
It is also written as follows:
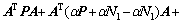

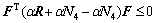 (56)
(56)
Inequality (56) can be equivalently transformed into
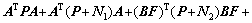
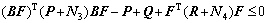 (57)
(57)
and

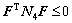 (58)
(58)
It is evident that inequality (56) is true if and only if inequality (57) and inequality (58) hold. According to Ni≥0, i=1, 2, 3, 4, inequality (58) can be satisfied. Then, it only needs to guarantee that inequality (57) holds

 (59)
(59)
Pre-and post-multiply by X and its transpose, respectively. It can be calculated that
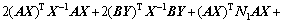
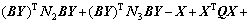
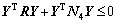 (60)
(60)
Applying to the Schur complement, one has
 (61)
(61)
As for nonlinear terms

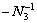 and
and 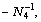 there are the following inequalities:
there are the following inequalities:
 (62)
(62)
 (63)
(63)
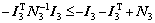 (64)
(64)
 (65)
(65)
Inequality (51) can be obtained. The proof is completed.
Theorem 4: Consider that the linear discrete-time system is subject to randomly occurred packet loss. At time k, if the optimization problem is feasible, then, for all time instants t>k, it is also feasible. Moreover, based on the feasibility property, the closed-loop system (7) is asymptotically stable with the state feedback gain matrix as F=YX-1.
Proof: Feasibility. Assume that the optimization problem is feasible at time k. Note that condition (16) is the mere constraint dependent on the states of the closed-loop system, then it only needs to prove that condition (16) is feasible for all future system states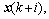
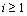 . When conditions (16) and (17) can be satisfied,
. When conditions (16) and (17) can be satisfied,  holds. Consider that the measured state
holds. Consider that the measured state 
 at time k+1. Then, it can be concluded very easy that
at time k+1. Then, it can be concluded very easy that  holds. Therefore, the feasible solutions of optimization problem at time k are also feasible solutions at time k+1. Similarly, this argument can be continued for time k+2, k+3, ….
holds. Therefore, the feasible solutions of optimization problem at time k are also feasible solutions at time k+1. Similarly, this argument can be continued for time k+2, k+3, ….
Proof: Robust stability. Based on the proof of feasibility, at time k+1, we can construct the same feasible solution as that at time k. Furthermore, the following Lyapunov function
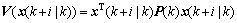
needs to be established, where P(k) is the optimal solution of optimization problem at time k. At time k+1, one has
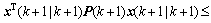
 (66)
(66)
This is because P(k+1) is optimal, but P(k) is only feasible at time k+1. According to inequality (11), when i=0, one can get
 (67)
(67)
Meanwhile, according to Eq. (7), it has
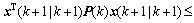
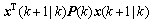 (68)
(68)
Combining inequlities (66), (67) and (68), the following inequality can be obtained:

 (69)
(69)
The Lyapunov function is strictly decreasing for the closed-loop system. Therefore, the closed- loop system is asymptotically stable. The proof is completed.
4 Numerical examples
In this paper, the continuous stirred tank reactor and four-tank system are considered to illustrate the effectiveness of proposed method. The control system setup in the experiment is shown in Figure 2. The physical entities are connected with wireless network nodes by I/O channel. The dynamic process data are transmitted to a computer control module by using TCP/IP protocol. An interface has been developed using the OLE for process control (OPC) server, which allows controllers running by MATLAB to be used on the physical systems.
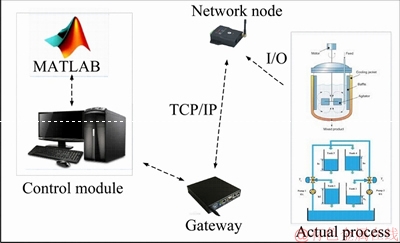
Figure 2 Control system setup in experiment
Example 1: Continuously stirred tank reactor
Reactors are very key units in chemical processes. These reactors have many different forms, but one of the most common idealizations is the typical continuously stirred tank reactor (CSTR) [38, 39]. Figure 3 depicts the CSTR schematic. Considering a CSTR in which the irreversible exothermic reaction A→B occurs, the control target is that the output concentration very close to its steady state point. The energy and material balance equations are
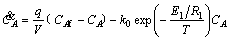
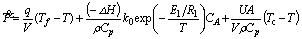 (70)
(70)

Figure 3 A continuous stirred tank reactor schematic
CA denotes the molar concentration. T represents the reactor temperature. Tc represents the temperature of the coolant stream. CAf denotes the input concentration of material A. The control target is to adjust T and CA by manipulating CAf and Tc. The nominal operating conditions correspond to the following equilibrium:
Teq=350 K,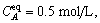
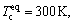

under the model parameters of experimental CSTR shown in Table 1.
Table 1 Model parameters of experimental CSTR

In order to research the dynamic behavior of CSTR in numerical simulation, the model should be discretized by the Euler backward method. Define the state vector  control vector
control vector  Sampling time is taken into account Ts=0.1 s. The system matrix A and the control matrix B are obtained from the linearized model of an industrial CSTR.
Sampling time is taken into account Ts=0.1 s. The system matrix A and the control matrix B are obtained from the linearized model of an industrial CSTR.
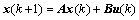
where

 .
.
The weighting matrices are selected as
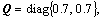
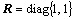 .
.
Initial states are selected as  Dropout-rate is selected as α=0.4 (see Figure 4).
Dropout-rate is selected as α=0.4 (see Figure 4).
The simulation results are shown in Figure 5 with the known dropout-rate case (red solid line), dropout-rate with uncertainty case (blue dashed line) and the unknown dropout-rate case (black dash-dot line), respectively. From Figure 5, when dropout-rate is known, the closed-loop system can achieve asymptotic stability with fast convergence, no overshoot and curve smoothing by using the proposed method. Moreover, when the Bernoulli variable α has the uncertainty and unknown cases, the system can still obtain the asymptotic stability.

Figure 4 Data losses instants

Figure 5 Response plot of closed-loop system in CSTR:
Example 2: Four-tank
This four-tank process is a very important system for control teaching and research [40, 41]. Figure 6 depicts the structure of four-tank. The pump of left side is used to supply water in the Tank 2 and Tank 4. The pump of right side is used to supply water in the Tank 1 and Tank 3, respectively. In addition, Tank 1, Tank 2, Tank 3 and Tank 4 have a water hole in bottom, respectively. Tank 4 discharges water into Tank 1. Tank 3 discharges water into Tank 2. Tank 1 and Tank 2 discharge water from the water outlet directly flowing back to the bottom of the large reservoir. There are some pipelines with a number of valves. By manual adjusting the opening of each valve, the outlet flow rate and the inlet flow rate of the water tank can be controlled, which can change the tank characteristics.
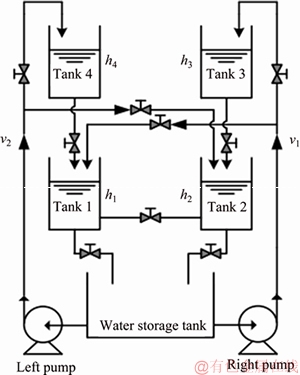
Figure 6 Structure of four-tank process
Assume that the cross-sectional areas of these four identical water tanks are S and the cross-sectional area of the bottom drain hole is a. The total flow of the right pump control is v1. The total flow of the left pump control is v2. hi (i=1, 2, 3, 4) are the height of the corresponding tank. γ1 is valve opening for v1 supply Tank 1. γ2 is valve opening for v2 supply Tank 2. According to Bernoulli’s principle (fluid mechanics), the four-tank control system corresponds to the following equation:

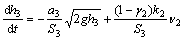 ,
,
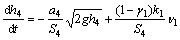 (71)
(71)
The model parameters for four-tank system are provided in Table 2
Table 2 Four-tank system model parameters for experiment

The state variables and control variables are defined: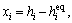
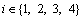 and
and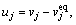
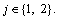 Therefore, the model is discretized by the Euler backward method, and Ts=0.1 s. The discrete-time model is obtained as follows:
Therefore, the model is discretized by the Euler backward method, and Ts=0.1 s. The discrete-time model is obtained as follows:

where


The weighting matrices are selected as
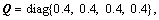
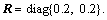
Initial states are selected as  dropout-rate is selected as α=0.9 (see Figure 7).
dropout-rate is selected as α=0.9 (see Figure 7).
Similar to the example 1, the simulation results are shown in Figure 8 with the known dropout-rate case (red solid line), dropout-rate with uncertainty case (blue dashed line) and the unknown dropout-rate case (black dash-dot line), respectively. When dropout-rate is α=0.9, the proposed RMPC method takes advantage of the rolling optimization way to solve the control input, which can achieve the asymptotic stability of system and overcome the bad effects of networked packet loss. It is worth mentioning when the Bernoulli variable α has uncertainty and unknown cases, the system can still achieve the expected optimal performance.

Figure 7 Data losses instants
In a word, in order to prove the effectiveness of proposed method, we will mainly proceed to compare with other methods in following two ways: 1) In technology aspect, the traditional known dropout-rate is divided into combination certainty part and norm-bounded uncertainty part and the unknown dropout-rate is also considered. Therefore, it is a more general case than most of those methods. What’s more, due to reducing the constraint of dropout-rate, the conservativeness of sufficient conditions can be greatly reduced. 2) In simulation aspect, we can see that both the dropout-rate with uncertainty case and the unknown dropout-rate case reach a same result as the known dropout-rate case. Moreover, it is worth mentioning that due to considering both the dropout-rate with uncertainty and the unknown dropout-rate, the allowable dropout-rate has become more relax.
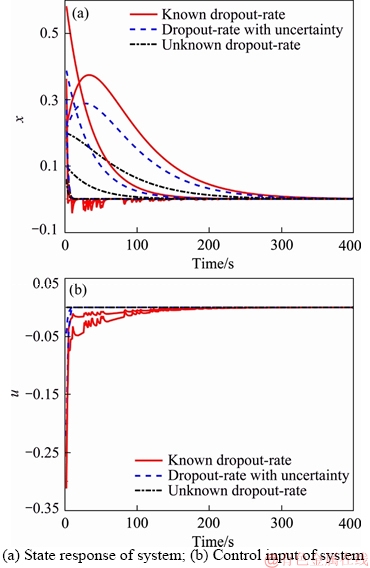
Figure 8 Response plot of closed-loop system in four-tank:
5 Conclusions
In this paper, for a class of linear discrete-time systems that is subject to randomly occurred packet loss in ICPSs, the novel RMPC approach has been proposed. Moreover, the probability distributions of packet loss have been described by the Bernoulli distributed white sequences. The existing sufficient conditions of the controller can be derived from solving a group of LMIs. Furthermore, in order to have a more comprehensive consideration, the unknown and uncertain cases of the dropout-rate have also been studied, which are more general than most of those in existing literatures for the discussed problems. At last, two simulation examples have been provided to illustrate the superiority, effectiveness and practicability of the proposed method. Furthermore, the future work is that when ICPSs are subject to network attack, the data loss problem of networked control system will be researched.
References
[1] YOSEF A, QUSAY H M. Cyber physical systems security: Analysis, challenges and solutions [J]. Computers & Security, 2017, 68: 81-97.
[2] BORJA B, RAM N A, TOM
N A, TOM S R, DIEGO M. Cyber physical systems: Extending pervasive sensing from control theory to the Internet of things [J]. Pervasive and Mobile Computing, 2017, 40: 156-184.
S R, DIEGO M. Cyber physical systems: Extending pervasive sensing from control theory to the Internet of things [J]. Pervasive and Mobile Computing, 2017, 40: 156-184.
[3] GAI Ke-ke, QIU Mei-kang, ZHAO Hui, SUN Xiao-tong. Resource management in sustainable cyber physical systems using heterogeneous cloud computing [J]. IEEE Transactions on Sustainable Computing, 2017, 99: 1-14.
[4] CINTUGLU M H, MOHAMMED O A, AKKAYA K, ULUAGAC A S. A survey on smart grid cyber physical system testbeds [J]. IEEE Communications Surveys & Tutorials, 2017, 19(1): 446-464.
[5] GU Lin, ZENG De-ze, GUO Song, BARNAWI A, XIANG Yong. Cost efficient resource management in fog computing supported medical cyber-physical system [J]. IEEE Transactions on Emerging Topics in Computing, 2017, 5(1): 108-119.
[6] YOUNG H C, HU Q, CLAIRE J. Tomlin secure estimation based Kalman Filter for cyber–physical systems against sensor attacks [J]. Automatica, 2018, 95: 399-412.
[7] LU An-yang, YANG Guang-hong. Input-to-state stabilizing control for cyber-physical systems with multiple transmission channels under denial-of-service [J]. IEEE Transactions on Automatic Control, 2018, 63(6): 1813-1820.
[8] LEE J, BAGHERI B, KAO H A. A cyber physical systems architecture for industry 4.0-based manufacturing systems [J]. Manufacturing Letters, 2015, 3: 18-23.
[9] MOHAMMAD H M, ADAM M, DOMAGOJ T, SANDRA H. Error-dependent data scheduling in resource-aware multi-loop networked control systems [J]. Automatica, 2017, 81: 209-216.
[10] QU Feng-lin, HU Bin, GUAN Zhi-hong, WU Yong-hong, HE Ding-xin, ZHENG Ding-fu. Quantized stabilization of wireless networked control systems with packet losses [J]. ISA Transactions, 2016, 64: 92-97.
[11] REN Mi-feng, ZHANG Jian-hua, JIANG Man, YU Mei, XU Jin-liang. Minimum, (h, f) entropy control for non-gaussian stochastic networked control systems and its application to a networked DC motor control system [J]. IEEE Transactions on Control Systems Technology, 2015, 23(1): 406-411.
[12] WANG Ji-min, MA Shu-ping, ZHANG Cheng-hui, FU Min-yue. Observer-based control for singular nonhomogeneous markov jump systems with packet losses [J]. Journal of the Franklin Institute, 2018, 355: 6617-6637.
[13] YAN Jing-jing, XIA Yuan-qing, WEN Cheng-lin. Quantized stabilization of switched systems with switching delays and packet loss [J]. Journal of the Franklin Institute, 2018, 355: 5351-5366.
[14] ZHU Kai-qun, SONG Yan, DING De-rui. Resilient RMPC for polytopic uncertain systems under TOD protocol: A switched system approach [J]. International Journal of Robust Nonlinear Control, 2018, 28(16): 5103-5117. DOI: 10.1002/rnc.4307.
[15] DOLK V, HEEMELS M. Event-triggered control systems under packet losses [J]. Automatica, 2017, 80: 143-155.
[16] ZHU Kai-qun, SONG Yan, DING De-rui, WEI Guo-liang, LIU Hong-jian. Robust MPC under event-triggered mechanism and round-robin protocol: An average dwell-time approach [J]. Information Sciences, 2018, 457-458: 126-140. DOI: 10.1016/j.ins.2018.04.052.
[17] SHEN Dong, ZHANG Chao, XU Yun. Intermittent and successive ILC for stochastic nonlinear systems with random data dropouts [J]. Asian Journal of Control, 2018, 20(3): 1102-1114.
[18] SU Cheng-li, LI Ping. Adaptive predictive functional control based on Takagi-Sugeno model and its application to PH process [J]. Journal of Central South University of Technology, 2010, 17(2): 363-371.
[19] SHI Hui-yuan, SU Cheng-li, CAO Jiang-tao, LI Ping, SONG Ying-li, LI Ning-bo. Incremental multivariable predictive functional control and its application in a gas fractionation unit [J]. Journal of Central South University, 2015, 22(12): 4653-4668.
[20] MAYNE D Q, RAWLINGS J B, RAO C V, SCOKAERT P. Constrained model predictive control: Stability and optimality [J]. Automatica, 2000, 36: 789-814.
[21] QIN S J, BADGWELL T A. A survey of industrial model predictive control technology [J]. Control Engineering Practice, 2003, 11(7): 733-764.
[22] LI Da-zi, JIA Yuan-xin, LI Quan-shan, JIN Qi-bing. Identification and nonlinear model predictive control of MIMO Hammerstein system with constraints [J]. Journal of Central South University, 2017, 24(2): 448-458.
[23] SONG Zheng-yu, YAN Gang-feng, ZHAO Dang-jun. ESO-based robust predictive control of lunar module with fuel sloshing dynamics [J]. Journal of Central South University, 2017, 24(3): 589-598.
[24] LI Yan, CHEN Xue-yuan, MAO Zhi-zhong. Model predictive control synthesis algorithm based on polytopic terminal region for Hammerstein-Wiener nonlinear systems [J]. Journal of Central South University, 2017, 24(9): 2028-2034.
[25] KOTHARE M V, BALAKRISHNAN V, MORARI M. Robust constrained model predictive control using linear matrix inequalities [J]. Automatica, 1996, 32(10): 1361-1379.
[26] WANG Jian-hua, SONG Yan, ZHANG Sun-jie, LIU Shuai, ABDULLAH M. D. Robust model predictive control for linear discrete-time system with saturated inputs and randomly occurring uncertainties [J]. Asian Journal of Control, 2018, 20(1): 425-436.
[27] YU Ji-min, NAN Liang-sheng, TANG Xiao-ming, WANG Ping. Model predictive control of nonlinear systems over networks with data quantization and packet loss [J]. ISA Transactions, 2015, 59: 1-9.
[28] SONG Yan, WEI Guo-liang, LIU Shuai. Distributed output feedback MPC with randomly occurring actuator saturation and packet loss [J]. International Journal of Robust & Nonlinear Control, 2016, 26(14): 3036-3057.
[29] SONG Yan, WANG Zi-dong, DING De-rui, WEI Guo-liang. Robust H2/H∞ model predictive control for linear systems with polytopic uncertainties under weighted MEF-TOD protocol [J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2018, 49(7): 1470-1481. DOI:10.1109/TSMC.2017.2757760.
[30] SONG Yan, WANG Zi-dong, LIU Shuai, WEI Guo-liang. N-step MPC with persistent bounded disturbances under stochastic communication protocol [J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2018. DOI: 10.1109/ TSMC.2018.2862406.
[31] FRANZ G, TEDESCO F, FAMULARO D. Model predictive control for constrained networked systems subject to data losses [J]. Automatica, 2015, 54: 272-278.
G, TEDESCO F, FAMULARO D. Model predictive control for constrained networked systems subject to data losses [J]. Automatica, 2015, 54: 272-278.
[32] LI Shuang, LIU Guo-ping. Networked predictive control for nonlinear systems with stochastic disturbances in the presence of data losses [J]. Neurocomputing, 2016, 194: 56-64.
[33] PANG Zhong-hua, LIU Guo-ping, ZHOU Dong-hua, SUN De-hui. Data-based predictive control for networked nonlinear systems with network-induced delay and packet dropout [J]. IEEE Transactions on Industrial Electronics, 2016, 63(2): 1249-1257.
[34] HASHIMOTO K, ADACHI S, DIMAROGONAS D V. Event-triggered intermittent sampling for nonlinear model predictive control [J]. Automatica , 2017, 81: 148-155.
[35] ZOU Yuan-yuan, LAM J, NIU Yu-gang, LI De-wei. Constrained predictive control synthesis for quantized systems with markovian data loss [J]. Automatica, 2015, 55: 217-225.
[36] TANG Xiao-ming, LI Deng, YU Ji-min, QU Hong-chun. Output feedback predictive control of interval type-2 T–S fuzzy systems with markovian packet loss [J]. IEEE Transactions on Fuzzy Systems, 2018, 26(4): 2450-2459.
[37] PRABHAT K M, DEBASISH C, DANIEL E Q. Stabilizing stochastic predictive control under Bernoulli dropouts [J]. IEEE Transactions on Automatic Control, 2018, 63(6): 1579-1590.
[38] GAO Hui-jun, CHEN Tong-wen, WANG L. Robust fault detection with missing measurements [J]. International Journal of Control, 2008, 81(5): 804-819.
[39] DONG Hong-li, WANG Zi-dong, SHEN Bo, DING De-rui. Variance-constrained H∞ control for a class of nonlinear stochastic discrete time-varying systems [J]. Automatica, 2016, 72: 28-36.
[40] CHENG Jun, CHEN Shi-qiang, LIU Zhi-jun, WANG Hai-ling, LI Jin. Robust finite-time sampled-data control of linear systems subject to random occurring delays and its application to four-tank system [J]. Applied Mathematics & Computation, 2016, 281: 55-76.
[41] HOUSSEMEDDINE G, SALIM H S, NABIL B, FAOUZI M. Generalized predictive control for a coupled four tank MIMO system using a continuous-discrete time observer [J]. ISA Transactions, 2017, 67: 280-292.
(Edited by HE Yun-bin)
中文导读
带有随机网络丢包的工业信息物理系统的鲁棒模型预测控制器设计
摘要:在工业信息物理系统中,针对一类遭受随机网络丢包的线性离散时间系统,提出了一种新颖的具有主动补偿机制的鲁棒模型预测控制方法。首先,将网络丢包的过程描述成伯努利概率分布;然后,通过利用Lyapunov稳定性理论,求解一组线性矩阵不等式获得控制器存在的充分条件。此外,本文考虑了丢包率具有不确定性和未知的两种情况,大幅度降低了控制器的保守性。设计的鲁棒模型预测控制方法不仅能有效地清除工业信息物理系统中的网络丢包问题带来的负面影响,而且还能保证闭环系统的稳定性。最后,利用两个仿真例子证明提出方法的优越性和有效性。
关键词:鲁棒模型预测控制;网络控制系统;丢包;线性矩阵不等式(LMIs)
Foundation item: Project(61673199) supported by the National Natural Science Foundation of China; Project(ICT1800400) supported by the Open Research Project of the State Key Laboratory of Industrial Control Technology, Zhejiang University, China
Received date: 2018-05-28; Accepted date: 2018-12-10
Corresponding author: CAI Hong-bin, PhD; Tel: +86-15898381920; E-mail: lnshhongbin@163.com; ORCID: 0000-0003-3770-7731

