J. Cent. South Univ. (2016) 23: 3183-3191

DOI: 10.1007/s11771-016-3384-6

Role based access control design using Triadic concept analysis

Ch. Aswani Kumar¹, S. Chandra Mouliswaran¹, LI Jin-hai², C. Chandrasekar³

1. School of Information Technology & Engineering, VIT University, Vellore 632014, India;

2. Faculty of Science, Kunming University of Science and Technology, Kunming 650500, China;

3. Department of Computer Science, Periyar University, Salem, India

Central South University Press and Springer-Verlag Berlin Heidelberg 2016

Abstract: Role based access control is one of the widely used access control models. There are investigations in the literature that use knowledge representation mechanisms such as formal concept analysis (FCA), description logics, and Ontology for representing access control mechanism. However, while using FCA, investigations reported in the literature so far work on the logic that transforms the three dimensional access control matrix into dyadic formal contexts. This transformation is mainly to derive the formal concepts, lattice structure and implications to represent role hierarchy and constraints of RBAC. In this work, we propose a methodology that models RBAC using triadic FCA without transforming the triadic access control matrix into dyadic formal contexts.Our discussion is on two lines of inquiry. We present how triadic FCA can provide a suitable representation of RBAC policy and we demonstrate how this representation follows role hierarchy and constraints of RBAC on sample healthcare network available in the literature.

Key words: access control; concept lattice; role based access control; role hierarchy; triadic context; triadic concept analysis

1 Introduction

Access control is one of the important and challenging security mechanisms. An access control system contains a collection of components and methods that set and control access privileges of legitimate users based upon the access permissions specified in the access policy [1-3]. There are varieties of models that represent and enforce access control systems. Traditional models are classified as discretionary access control (DAC), mandatory access control (MAC) and role based access control (RBAC) [4]. Among these models RBAC is widely accepted and deployed models. The motivation behind RBAC is that a subject’s functionality is more important than whom the subject is [2]. RBAC has been studied thoroughly and several logical approaches were proposed in the literature to formalize this model [5]. In addition to its application in enterprise systems, RBAC is implemented in system software such as UNIX like operating systems and application software such as database management systems. The main advantage of RBAC is that it is policy neutral such that by using role hierarchies, constraints within RBAC, a wide range of security policies can be expressed [6-8]. FERRAIOLO et al [3] have described that access control policy can be represented a priori and can be maintained by the security administrator for effective enforcement of the policy. A formal representation of policy will help in designing and implementing in applications [8]. Further a logical representation or a framework of the policy can help in verifying its correctness [9]. KIM et al [8] have analyzed the need for modeling RBAC from a development perspective. There are investigations in the literature on modeling RBAC using different frameworks such as description logics [10-12], conceptual graphs [13], Ontologies [14-16], formal concept analysis [17-19].

Formal concept analysis (FCA) is a mathematical framework based upon lattice theory principles and mainly used for knowledge representation, extraction and analysis [20-24]. Underlying structure of FCA is a formal context defined as (G, M, Y) where G is the set of objects, M is the set of attributes and Y is the binary relation between these two sets. This structure is also known as dyadic context. There are investigations reported in the literature on adopting FCA for modeling RBAC by considering access control matrix as formal context [15, 17, 19, 25-28]. However, during such adoption of FCA, the three dimensional RBAC matrix is transformed into dyadic formal contexts. On transforming to the dyadic context, FCA algorithm was applied to perform concept lattice construction, attribute exploration, implications in order to derive the RBAC role hierarchy, SoD constraints etc. However, from the basic settings of dyadic case, FCA is extended into triadic case where the input data would be three dimensional relational data represented in a table called triadic context [29-32]. The entries of the table indicate which objects have which attributes under what conditions. Such a representation is analogous to the RBAC three dimensional data. However, there are no investigations reported in the literature adopting triadic FCA to process triadic context directly without transforming it into dyadic contexts. Based on these observations, motivated by the recent investigations on triadic FCA [33-35] and extending upon the contributions of KNECHTEL [15] and OBIEDKOV et al [25], in this work, we propose a new approach for modeling RBAC using triadic FCA.

2 Background

In this section, we provide a brief background on RBAC and related work on representing RBAC. Further, we also define the objectives that we are trying to achieve in this work.

2.1 RBAC

RBAC has become de facto standard for enforcing access control in enterprise systems due to its simplification in deployment and administering access control policies. This policy was initially proposed by Sandhu in 1996 [36] and later standardized by NIST [2-3]. Instead of assigning access permissions to individuals, RBAC assigns them to roles. Hence a user is permitted to execute access permissions that are assigned to the role he/she corresponds to. A role maps each user to a set of permissions. RBAC model supports three important security principles i.e. data abstraction, least privilege and separation of duty. The NIST standard divides RBAC into core RBAC, hierarchical RBAC and constrained RBAC [2]. Core RBAC contains basic functionalities of RBAC. Hierarchical RBAC follows role hierarchies in addition to core RBAC functionalities. Constrained RBAC follows constraints such as Separation of Duty (SoD) [37].

Since RBAC is well established in the literature, RBAC fundamentals, its constituents and its constraints are omitted in this discussion.In order to read these missing details, readers can refer to FADHEL et al [5] who recently discussed taxonomy of RBAC models, constraints and several extensions of RBAC. Further, NIST documentation is standard reference point on RBAC [2]. CHEN [38] has analyzed different issues of RBAC such as permission usage relation, role activation and computational complexity. KUHN et al [39] have discussed the difficulties with RBAC and suggested merging of attribute based access control (ABAC) and RBAC. COYNE and WEIL [40] have analyzed the ABAC and RBAC in detail. MARTINEZ-GARCIA et al [6] have extended RBAC using fuzzy relations. This fuzzy RBAC is applicable in the environments where authorization related information is fuzzy. In an interesting work, UNAL and CAGLAYAN [41] have discussed a formal RBAC model for multi-domain mobile network.

ZHAO et al [9] have mentioned different logical frameworks available for representing an access policy.In a technical report, ZHANG et al [12] have shown how domain specific description logics can be used for access control. KIM et al [8] have proposed feature based modeling approach to RBAC.

2.2 Problem description and research question

RBAC role matrix is represented as a three dimensional matrix with roles (R), document objects (D) and access permissions (P). This matrix is formalized as a triadic context. This formal context depicts the relations among these three components of RBAC.However investigations reported in the literature have transformed this formal triadic context into dyadic contexts for applying FCA. This transformation is made by considering the cross product of any of the two elements of the triadic context as objects and remaining element as attributes of the dyadic context. For example, triadic context (R, D, P, Y) is transformed into dyadic case as (R×D, P, Y^R×D,P) [15, 17]. Further it is proved in the literature that the concept lattice, attribute implications obtained from such analysis follow the role hierarchy and RBAC constraints such as SoD. In FCA literature, conventional dyadic algorithms of FCA are successfully extended to triadic contexts [33, 42-44]. However, representing RBAC through triadic FCA is not yet reported in the literature. Based on these observations, the following research questions are addressed in this paper:

How triadic concept analysis provides suitable formal representation of a RBAC policy?

What would be the interpretation of triadic labeled lattice hierarchy produced from the triadic RBAC matrix?

Does this representation follow the constraints and implicit permissions laid by the policy?

We aimed at these objectives such that without transforming the RBAC triadic context, we can model the RBAC policy through tri-concepts, tri-lattice and implications.

2.3 Related work

FCA is used in the literature to model the access control policies. By considering access control matrix as a formal context, FCA based methods are studied for implementing access control policies [15, 17, 26]. OBIEDKOV et al [25] have shown how attribute exploration process in FCA can be used to build lattice based access control in an interactive manner. SOBIESKI and ZIELINSKI [26] have modeled the role hierarchy of RBAC using FCA. SELLAMI et al [19] have proposed FCA based secure data integration approach for combining local access control policies. HAN et al [27] have performed role mining with the help of concept lattice model. Further, they have generated a critical mapping between attribute and permission sets. In an important contribution, KNECHTEL [15] has provided a methodology to represent RBAC with the help of Ontologies and Description logics (DL). To accomplish this, KNECHTEL [15] has used FCA to assign labels to Ontology axioms. As mentioned, this work is achieved by transforming triadic RBAC matrix into dyadic cases. Extending upon this, Aswani KUMAR [17] has proposed a method to design RBAC using FCA. Very recently, FCA is used to model the Chinese wall access control, inter-domain role based access control and fuzzy FCA for modeling fuzzy RBAC [45-47]. As discussed, all these investigations have used dyadic formal context in their analysis.

3 Triadic FCA

FCA in classical setting i.e. dyadic formal context having binary relation between objects and attributes of the context is discussed widely in the literature. For basic familiarities we point to some authoritative references such as [21-24, 48-52] to the readers. LEHMAN and WILLE [29] have extended the classical FCA in dyadic case to triadic setting. GANTER and OBIEDKOV [32] have discussed on deriving implications from triadic contexts. BELOHLAVEK and OSICKA [53-55] have extended the triadic FCA from binary settings to fuzzy settings. Fuzzy valued triadic implications are discussed by GLODEANU [35]. KAYTOUE et al [34] have discussed the links between bi-clustering numerical data and triadic FCA. Very recently IGNATOV et al [33] have discussed triadic FCA and tri-clustering. ZHUK et al [56] have discussed triadic data classification. Further they have defined optimal patterns in triadic data.VOUTSADAKIS [57] has discussed generalization of the triadic FCA to polyadic i.e. n-dimensional concept analysis. Recently TANG et al [58] have discussed the triadic formal concept analysis for cognitive system model.

Definition 1 (Formal context): The main notion of FCA is formal context which is represented as cross- table. Formally, it is defined as a triple of sets (G, M, I) where G is set of objects represented as rows, M is set of attributes and I is the binary relation between the objects and attributes I 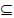G×M.

Definition 2 (Galois operators): A formal context K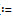(G, M, I) induces a set of operators known as Galois operators ↑, ↓ such that ^↑: 2^G→2^M and ^↓: 2^M→2^G formally defined as for C 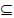G and D 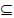M by

C^↑= {m∈ M | 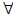g∈G: (g,m) ∈I}

D^↓= {g∈ G | 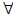m∈M: (g,m) ∈I}

These operators form a Galois connection between the power sets of sets G and M. A Galois connection induces closure operators (·)^↑↓ and realizes a one-one correspondence between all closed sets of objects and closed set of attributes. These operators are also known as concept forming operators.

Definition 3 (Formal concept): From a formal context K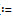(G, M, I), the concept forming operators (↓,↑) derives a pair (C,D) known as formal dyadic concept.This pair is known as extent (C) and intent (D) of the formal concept such that C^↑=D and D^↓=C.

Definition 4 (Concept lattice): The collection of all the concepts of a formal context K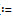(G, M, I) forms a partial ordered sub-concept and super-concept hierarchy. This hierarchical structure is known as concept lattice. These fundamentals of FCA in dyadic case are well discussed in the literature.For more details interested readers can refer to Refs. [22-23].

Definition 5 (Triadic context): A triadic context is a quadruple defined as K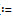(G, M, B, Y), where G, M, and B are respectively known as objects, attributes and conditions. Further Y is a ternary relation such that Y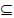G×M×B. This can be interpreted as an object g has an attribute m under the condition b, (g,m,b)∈Y .

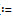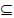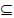Definition 6 (Triadic concept): A triadic concept of triadic context K(G, M, B, Y), is defined as a triple (A₁, A₂, A₃) where A₁ G, A₂ M, A₃ 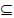B satisfying the condition that A₁×A₂×A₃ 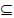Y such that none of its components can be enlarged without violating this condition. A₁, A₂, A₃ are known as extent, intent and modus of the concept (A₁, A₂, A₃). This definition can be regarded as a natural extension of the definition of a formal dyadic concept to triadic case. In the triadic context, triadic concept denotes a maximal rectangular parallelepiped of crosses i.e. a triadic concept is regarded as a maximal cuboid, full of crosses. Considering a triadic context K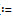(X₁, X₂, X₃, Y), we can build three dyadic formal contexts defined as

K⁽¹⁾= (X₁, X₂×X₃, Y⁽¹⁾)

K⁽²⁾= (X₂, X₁×X₃, Y⁽²⁾)

K⁽³⁾= (X₃, X₁×X₂, Y⁽³⁾)

where x₁ Y⁽¹⁾ (x₂,x₃):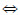 x₂ Y⁽²⁾ (x₁,x₃) : 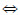x₃ Y⁽³⁾ (x₁,x₂) : 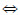(x₁,x₂,x₃) ∈Y. The concept formation operators induced by K⁽ⁱ⁾ are denoted by (-)⁽ⁱ⁾. Similar to regular dyadic formal context, each induced context would have two such derivation operators [29-33].

Definition 7 (Tri-concept forming operator–Outer derivation): For {i,j,k}={1,2,3}with and for Z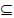X_iand W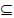X_j×X_k,the (-)⁽ⁱ⁾ derivation operators are defined by

Ψ: Z →Z⁽ⁱ⁾: {(x_j,x_k) ∈ X_j×X_k | (x_i,x_j,x_k) ∈ Y 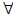x_i∈Z}

Ψ′: W →W⁽ⁱ⁾: { x_i∈ X_i | (x_i,x_j,x_k) ∈ Y 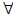( x_j,x_k) ∈W}

These operators yield the above given three dyadic formal contexts K⁽¹⁾, K⁽²⁾ , K⁽³⁾. i.e. K⁽ⁱ⁾ =(X_i, X_j× X_k, Y⁽ⁱ⁾) for {i,j,k}={1, 2, 3}. Due to the structure of triadic contexts, for obtaining triadic concepts, we require further derivation operators defined as follows.

Definition 8 (Tri-concept forming operator–Inner derivation): For {i,j,k}={1,2,3} and for Z_i 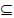X_i, Z_j 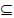X_j, Z_k 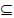X_k, the (i,j, Z_k) derivation operators are defined by

Φ: Z_i →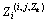:{x_j∈X_j | (x_i,x_j,x_k)∈Y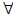( x_i,x_k)∈Z_i×X_k}

Φ′: Z_j →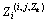: {x_i∈X_i |(x_i,x_j,x_k)∈Y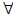(x_j,x_k)∈Z_j×X_k}

This inner operator derives the context 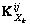=(X_i, X_j, 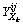) where (x_i, x_j)∈ 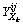iff (x_i,x_j,x_k)∈Y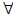x_k∈X_k. Here (x_i,x_j)∈ 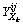can be referred as object x_i has attribute x_j under all conditions of x_k with x_k∈X_k.

The operators Ψ and Ψ′ are known as outer operators and composition of both is known as outer closure [29]. Similarly the operators Φ and Φ′ are known as inner operators and their composition is inner closure. So in order to generate a triadic concept with Z₁ in its extent, the first step would be to generate a dyadic concept in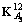. Further triadic concept would be obtained by extending 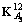using the corresponding derivation operator in K⁽³⁾.

Definition 9 (Triadic concept formation): A concept having Z₁ in its extent can be defined as

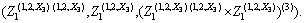
This formation process first fixes a non-empty object set Z₁. Then it finds the set of attributes which all objects of Z₁ have under all the conditions given in X₃. Then Z₁ is extended to the set of all objects having all those attributes under all conditions of X₃. At the end, X₃ is extended to the set of all conditions under which each of the derived objects has each of the derived attributes.

Definition 10 (Concept tri-lattice): For each i∈{1, 2, 3}, there is a quasiorder 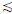_i and its corresponding equivalence relation ～_i defined by (A₁,A₂,A₃) 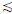_i (B₁,B₂,B₃): 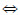A_i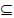B_i and (A₁,A₂,A₃) ～_i (B₁,B₂,B₃): A_i=B_i (i=1, 2, 3). The set of all triadic concepts ordered in this way forms concept tri-lattice.

However the fundamental difference with concept lattice structures of dyadic contexts is that the concept tri-lattices does not form partial order by extent inclusion as the same extent may form concepts with combinations of different other intent and modus components [29].

This triadic lattice structure is regarded as a symmetric structure where the set of objects, attributes and conditions are all treated equally [59]. Generally this structure is drawn as a triangular graph. For a better understanding, we can draw complete lattices for extents, intents and modi each. Since these are drawn along the sides of triangular graph, they are called as side lattices [29]. Recently, three-way analysis of FCA is new concept under investigation [60].

4 Proposed methodology

The main objective of our work is to apply FCA on the three dimensional access control matrix without transforming it into dyadic formal contexts. To achieve this objective, we propose the methodology that exploits the inner and outer closure operations defined above:

1) Identify the roles (R), data objects (D) and access permissions (P) from the given policy.

2) Form the three dimensional access matrix having roles (R), data objects (D) and permissions (P) as a triadic context:

K_R,D,P:=(R,D,P,I), where I is the ternary relation among R, D and P.

3) For every permission set HP, compute the dyadic context using the inner closure operators defined above i.e. Φ and Φ′ i.e. (R, D×H, Y³).

4) Use the dyadic concept generation algorithms in Ref. [20] and compute the concepts for each of these contexts obtained in Step 3).

5) Then for each dyadic concept, compute the set of conditions that contains it using outer closure operators defined above i.e. Ψ and Ψ′.

6) Form the triadic concepts as given in Definition 9.

7) Repeat Step 5), for any subset of conditions.

8) Remove the redundant tri-concepts if any.

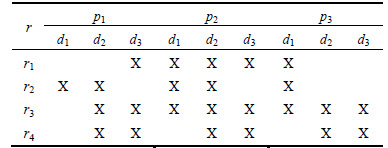
With the help of this methodology we derive triadic concepts from three-dimensional RBAC matrix. Algorithmically this process follows an exponential time. Other than this, we have algorithms such as TRIAS to find tri-concepts whose extent, intent and modus cardinalities are greater than the specified threshold values [42]. For a better understanding consider a small triadic RBAC context (R,D,P,Y) shown in the following Table 1. This context contains 4 roles, 3 documents and 3 permissions.

Now consider {i, j, k}={1, 2, 3}, X₁=R, X₂=D, X₃=P, A₃={p₁, p₂} and Z={r₃}. From this as per the definition 3.8, inner operator produces Φ(Z)={d₂, d₃} and Φ′Φ(Z)= {r₃, r₄}. Further the outer derivation operator from the definition 3.7 produces Ψ(Z)={(d₂, p₁), (d₃, p₁), (d₂, p₂),(d₃, p₂), (d₂, p₃), (d₃, p₃)}. From this we can notice that Ψ′(Ψ(Z))={r₃, r₄}. As per the triadic concept formation from definition 3.9 we get the triadic concept ({r₃, r₄}, {d₂, d₃}, {p₁, p₂, p₃}).

Table 1 RBAC triadic context

5 Experimental analysis

In order to demonstrate the proposed triadic FCA based methodology, we utilize a healthcare ad hoc network. More details of this network environment are available in the literature [17]. From this healthcare network we have identified 9 roles: Office assistant (R1), Health visitor (R2), Mother and child care unit Incharge (R3), Nurse (R4), OT Incharge (R5), Doctor (R6), Accountant (R7), Accounting manager (R8) and Internal auditor (R9). Figure 1 shows the role graph of this network. Following are the document objects in the network: Family folders (D1), Mother nutrition chart (D2), Vaccination information of child (D3), In-patient records (D4), OT-records (D5), Prescription records (D6), Health unit transaction records (D7) and Ledger reports (D8).Access permissions on these data objects include Create (P1), Delete (P2), Input/Modify (P3), Generate (P4) and Verify (P5).

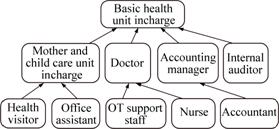
Fig. 1 Healthcare network role graph

Table 2 shows the triadic context of three dimensional access control matrix of health care network. We have applied the proposed methodology presented above. For each of the access permission, first we have applied inner closure operator and then followed by outer derivation operator. This triadic FCA has produced 17 tri-concepts listed in Table 3. As discussed, the extents, intents and modi of triadic concepts do not form a closure system unlike the dyadic case. The same we could observe from Table 3. For example tri-concept 9 indicates that the roles R7 and R8 in its extent have

Table 2 Formal triadic context of RBAC of healthcare network

Continued

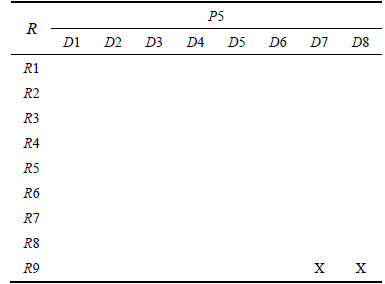
Table 3 Tri-concepts obtained from triadic context shown in Table 2

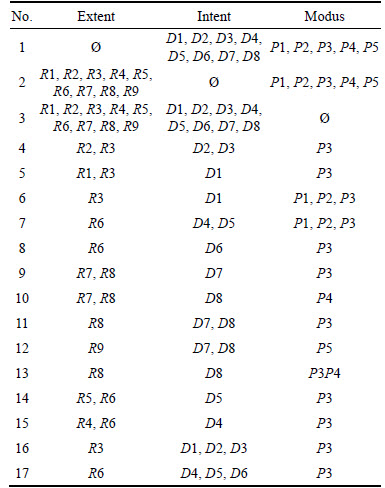
access to document D7 in intent under the permission P3 in the modus. However the same set of roles R7 and R8 are in extent of concept 10 as both these roles have access to document D8 under the permission P4.

Figure 2 shows the geometric structure of the triadic lattice obtained from the triadic concepts shown in the Table 3. Each circle shown in the diagram represents a triadic concept. This structure can be understood via the extent diagram on the right side, intent diagram on the left side and the modus diagram on the top. In RBAC applications, Roles are in the extent, data objects are in the intent and access permissions are in the modus. A circle shown on the line diagram in the right side represents the extent (roles) consisting of those objects that are attached to this circle below. i.e. extents get larger from lower left to upper right. Similarly intent gets larger from the upper left to lower right. Modus gets larger from upper right to lower left. Consider the circle that is placed at the center of the diagram and above the bottom node. This node has the extent {R2, R3} with the intent {D2, D3} at lower left and the modus {P3}.

In the classical dyadic case, concept lattice resulting from the dyadic RBAC formal context demonstrates the role and access permission hierarchy. Further dependencies among the roles, access permissions and documents can be derived such that size of the security lattice structure can be controlled [17, 25]. In the role hierarchy a role ‘r’ can inherit the role functionalities from the roles above it and connected to it.

We can observe that the side lattices shown on each side of the tri-lattice are complete lattices. Permission inheritance relation is applied on the user roles and this relation is known as role hierarchy in RBAC. The side lattice on the right side of the tri-lattice depicts the role hierarchy of the RBAC such that roles in the lower left can inherit the permissions from the roles connected above them. For example we can notice that R6 (Doctor) has the access permissions of R5 (OT incharge) and Nurse (R4). This observation is consistent with the RBAC matrix shown in Table 2.

Static SoD constraint defines a mutual exclusion among roles, permissions or users. It enforces certain conditions on the assignment of users to roles and roles to permissions based on this mutual exclusion or conflict relations. Hence same user would not be assigned conflicting roles. Similarly conflicting permissions would not be assigned to same role. As per the SoD constraints of this healthcare network, following are some of mutually exclusive roles: (R3 and R8), (R3 and R9), (R6 and R8), (R6 and R9), (R2 and R8), (R2 and R9). From the tri-lattice structure displayed in the Figure 2 we can notice such conflicting roles being separated in the hierarchy. Similarly we can observe the role precedence relationship from the role hierarchy [5].

In addition to the tri-lattice from the triadic context, we can derive triadic implications in similar to dyadic case. GANTER and OBIEDKOV [32] have described several families of implications that can be generated from the triadic context. Recently GLODEANU [35] has extended this to generate fuzzy implications. For a triadic context K(G, M, B, Y), GANTER and OBIEDKOV [32] have discussed the conditional attribute implications which are of the form S T where S, T 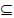M and C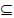B. Such expression can be read as S implies T under all conditions from C. This conditional implication holds in the triadic context (G, M, B, Y) iff for each condition c∈C it holds that if an object g ∈G has all the attributes in S then it also has all the attributes in T. From the RBAC formal context shown in the Table 2, we can obtain triadic implications that represent the dependencies among the roles, document objects and access permissions. For example considering S={D2}, T={D3} and C={P3}, we can obtain the implication D2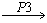D3. This can be understood as the roles that can access the mother nutrition chart (D2) under the access permission Input/Modify (P3) condition can also access the vaccination information of child (D3) with same access permission (P3). From the triadic context shown in Table 2 we can notice that Health visitor (R2) and Mother and child care unit Incharge (R3) are the two roles that hold this implication. Similarly we can obtainanother implication D4 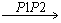D5. This implication can be read as Doctor can create and delete the IP records, OT records. Further, triadic context exhibit six fold symmetry such that the objects, attributes and conditions of the context can be interchanged [32, 35]. Hence by exchanging attributes and conditions, we can obtain attributional condition implications. From the RBAC triadic context by considering S, T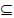B and C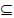M, we get attributional condition implications of the form ST. From the triadic context shown in Table 2, we can obtain P3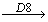P4. This implication can be understood as the roles that have access permission of Input/Modify (P3) with Ledger Report (D8) can also have the access permission of Generate (P4). From the triadic context shown in Table 2, we can notice the Accounting Manager (R8) is the role that holds this implication. Similarly, we can obtain another implicationP1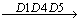P2, P3. This implication can be read as the roles that have the access permission of Create (P1) with document objects Family folders (D1) or In-patient records (D4) or OT-records (D5) can also have the access permission of Delete (P2) and Input/Modify (P3). From the triadic context shown in Table 2, we can notice that MCU Incharge (R3) and Doctor (R6) are the two roles hold this implication. Hence these conditional attribute implications and attributional condition implications derive the functional dependencies among non-mutually exclusive roles, documents and access permissions.

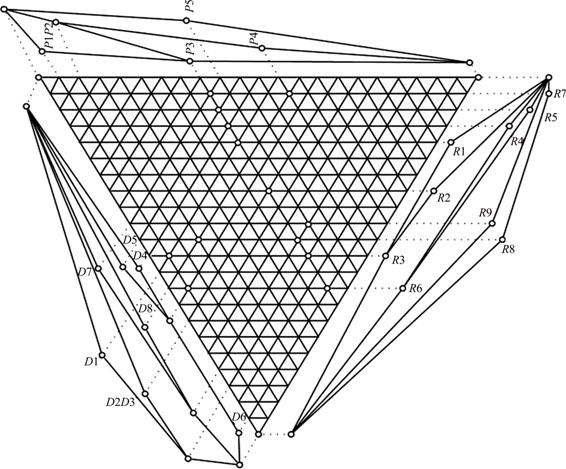
Fig. 2 Triadic lattice of RBAC

The proposed model has the following advantages. First it makes possible to directly obtain the role hierarchy and SoD constraints from the triadic contexts. The proposal therefore can avoid transforming the triadic RBAC context into different dyadic contexts for modeling the policy. Second the dependencies among the RBAC constituents (R, D, P) can be captured by the triadic concepts and conditional attribute implications derived from them. The resulting tri-lattice role hierarchy would help the security engineers to verify the effect of user role hierarchy and dependencies. In particular, the proposed methodology and its solutions help the administrative model for RBAC proposed by SANDHU [36].

6 Conclusions

1) With the proposed methodology, we have represented RBAC three-dimensional matrix as triadic lattice structure thereby achieving role hierarchy and separation of duty constraints without transforming the triadic context into dyadic formal contexts.

2) We have provided the interpretation of triadic labeled lattice hierarchy produced from the triadic RBAC matrix.

3) Conditional attribute implications derived from the triadic context demonstrate the dependencies among the RBAC elements.

4) The proposed method helps in representing RBAC policy through triadic FCA which further can be enforced in an access control system.

Acknowledgement

One of the authors, Ch. Aswani Kumar, sincerely acknowledges the financial support from Department of Science and Technology, Government of India under the grant: SR/CSRI/118/2014.

References

[1] SANDHU R S. Lattice-based access control models [J]. Computer, 1993, 26(11): 9-19.

[2] SANDHU R, FERRAIOLO D, KUHN R. The NIST model for role-based access control: Towards a unified standard [C]// ACM Workshop on Role-based Access Control. Berlin: ACM Digital Library, 2000: 47-63.

[3] FERRAIOLO D F, SANDHU R, GAVRILA S, KHUN D R, CHANDRAMOULI R. Proposed NIST standard for role-based access control [J]. ACM Transactions on Information and System Security, 2001, 4(3): 224-274.

[4] BISHOP M. Introduction to computer security [M]. Boston: Addison- Wesley, 2005: 26-64.

[5] FADHEL A B, BIANCULLI D, BRIAND L. A comprehensive modeling framework for role-based access control policies [J]. Journal of Systems and Software, 2015, 107: 110-126.

[6] C, NAVARRO-ARRIBA G, BORRELL J. Fuzzy role-based access control [J]. Information Processing Letters, 2011, 111(10): 483-487.

[7] HUANG H, SHANG F, LIU J. Handling least privilege problem and role mining in RBAC [J]. Journal of Combinatorial Optimization, 2013, 30(1): 1-24.

[8] KIM S, KIM D K, LU L, KIM S, PARK S. A feature-based approach for modeling role-based access control systems [J]. Journal of Systems and Software, 2011, 84(12): 2035-2052.

[9] ZHAO C, HEILILI N, LIU S, LIN Z. Representation and reasoning on rbac: A description logic approach [C]// Intel Colloquium on Theoretical Aspects of Computing. Hanoi: Springer Berlin Heidelberg, 2005, 3722: 381-393.

[10] CHAE J. Modeling of the role-based access control policy with constraints using description logic [C]// Intel Conference on Computational Science and its Applications. Kuala Lumpur: Springer Berlin Heidelberg, 2007, 4705: 500-511.

[11] ZHANG R, ARTALE A, GIUNCHIGLIA F, CRISPO B. Using description logics in relation based access control [R]. Italy: University of Trento, 2009.

[12] BERTINO E, FERRARI E, ATLURI V. The specification and enforcement of authorization constraints in workflow management systems [J]. ACM Transactions on Information and System Security, 1999, 2(1): 65-104.

[13] THION R, COULONDRE S. Representation and reasoning on role-based access control policies with conceptual graphs [C]// Intel Conference on Conceptual Structures. Denmark: Springer Berlin Heidelberg, 2006, 4068: 427-440.

[14] CHOI C, CHOI J, KIM P. Ontology-based access control model for security policy reasoning in cloud computing [J]. The Journal of Supercomputing, 2014, 67(3): 711-722.

[15] KNECHTEL M. Access restrictions to and with description logic web ontologies [D]. Dresden: Technische Dresden, 2011.

[16] MOULISWARAN S C, KUMAR C A, CHANDRASEKAR C. Inter-domain role based access control using ontology [C]// IEEE Intel Conference on Advances in Computing, Communications and Informatics. Kochi: IEEE Press, 2015: 2027-2032.

[17] KUMAR C. Designing role-based access control using formal concept analysis [J]. Security and Communication Networks, 2013, 6(3): 373-383.

[18] JIAO S, LIU Y, HU H, WEI D, ZHANG Y. Dynamic policy access model based on formal concept analysis [C]// IEEE Intel Conference on Wireless Communications, Networking and Mobile Computing. Dalian: IEEE Press, 2008: 1-5.

[19] SELLAMI M, GAMMOUDI M M, HACI M S. Secure data integration: A formal concept analysis based approach [C]// Intel Conference on Database and Expert Systems Applications. Munich: Springer International Publishing, 2014, 8645: 326-333.

[20] KUMAR C A, SINGH P K. Knowledge representation using formal concept analysis: A study on concept generation [M]// Global Trends in Intelligent Computing Research and Development. IGI Global, 2013: 306-336.

[21] WILLE R. Conceptual graphs and formal concept analysis [C]// Intel Conference on Conceptual Structures. Washington: Springer Berlin Heidelberg, 1997, 1257: 290-303.

[22] STUMME G. Formal concept analysis [M]// Handbook on Ontologies. Springer Science & Business Media, 2013: 177-179.

[23] POELMANS J, KUZNETSOV S O, IGNATOV D I, DEDENE G. Formal concept analysis in knowledge processing: A survey on models and techniques [J]. Expert Systems with Applications, 2013, 40(16): 6601-6623.

[24] KUMAR C A, SRINIVAS S. Concept lattice reduction using fuzzy K-Means clustering [J]. Expert Systems with Applications, 2010, 37(3): 2696-2704.

[25] OBIEDKOV S, KOURIE D G, ELOFF J H. Building access control models with attribute exploration [J]. Computers & Security, 2009, 28(1/2): 2-7.

[26] B. Modelling role hierarchy structure using the formal concept analysis [J]. Annales UMCS Sectio AI Informatica, 2010, 10(2): 143-159.

[27] HAN D J, ZHUO H K, XIA L T, LI L. Permission and role automatic assigning of user in role-based access control [J]. Journal of Central South University, 2012, 19(4): 1049-1056.

[28] KUMAR C A. Modeling access permissions in role based access control using formal concept analysis [C]// Intel Conference on Information Processing. Bangalore: Springer Berlin Heidelberg, 2012, 292: 578-583.

[29] LEHMANN F, WILLE R. A triadic approach to formal concept analysis [C]// Intel Conference on Conceptual Structures. Santa Cruz: Springer Berlin Heidelberg, 1995, 954: 32-43.

[30] WILLE R. The basic theorem of triadic concept analysis [J]. Order, 1995, 12(2): 149-158.

[31] DAU F, WILLE R. On the modal understanding of triadic contexts [C]// Annual Conference on Classification and Information Processing at the Turn of the Millennium. University of Bielefeld: Springer Berlin Heidelberg, 2000: 83-94.

[32] GANTER B, OBIEDKOV S. Implications in triadic formal contexts [C]// Intel Conference on Conceptual Structures. Huntsville, USA: Springer Berlin Heidelberg, 2004, 3127: 186-195.

[33] IGNATOV D I, GNATYSHAK D V, KUZNETSOV S O, MIRKIN B G. Triadic formal concept analysis and triclustering: searching for optimal patterns [J]. Machine Learning, 2015, 101(1): 1-32.

[34] KAYTOUE M, KUZNETSOV S O, MACK J, NAPOLI A. Biclustering meets triadic concept analysis [J]. Annals of Mathematics and Artificial Intelligence, 2014, 70(1): 55-79.

[35] GLODEANU C V. Fuzzy-valued triadic implications [C]// Intel Conference on Concept Lattices and their Applications. Nancy, France: CLA, 2011: 159-173.

[36] SANDHU R. Role hierarchies and constraints for lattice-based access controls [C]// European Symposium on Research in Computer Security. Rome: Springer Berlin Heidelberg, 1996, 1146: 65-79.

[37] KUGBLENU F M, ASIM M. Separation of duty in role based access control system: A case study [D]. Sweden: Blekinge Institute of Technology, 2007.

[38] CHEN L. Analysing and developing role-based access control models [D]. London: Department of Mathematics Royal Holloway, University of London, 2011.

[39] KUHN D R, COYNE E J, WEIL T R. Adding attributes to role-based access control [J]. Computer, 2010, 43(6): 79-81.

[40] COYNE E, WEIL T R. ABAC and RBAC: Scalable, flexible, and auditable access management [J]. IT Professional, 2013, 15(3): 14-16.

[41] UNAL D, M U. A formal role-based access control model for security policies in multi-domain mobile networks [J]. Computer Networks, 2013, 57(1): 330-350.

[42] JASCHKE R, HOTHO A, SCHMITZ C, GANTER B, STUMME G. TRIAS-An algorithm for mining iceberg tri-lattices [C]// IEEE Intel Conference on Data Mining. Hong Kong: ICDM, 2006: 907-911.

[43] KONECNY J, OSICKA P. General approach to triadic concept analysis [J]. Society for Industrial and Applied Mathematics Review, 2009, 51(3): 455-500.

[44] STUMME G. A finite state model for on-line analytical processing in triadic contexts [C]// Intel Conference on Formal Concept Analysis. Lens, France: Springer Berlin Heidelberg, 2005, 3403: 315-328.

[45] MOULISWARAN S C, KUMAR C A, CHANDRASEKAR C. Modeling Chinese wall access control using formal concept analysis [C]// IEEE Intel Conference on Contemporary Computing and Informatics. Mysore: IEEE Press, 2014: 811-816.

[46] MOULISWARAN S C, KUMAR C A, CHANDRASEKAR C. Representation of multiple domain role based access control using FCA [C]// IEEE Intel Conference on Electrical, Computer and Communication Technologies. Coimbatore: IEEE Press, 2015, 2: 797-799.

[47] SUBRAMANIAN C, CHERUKURI A K, CHELLIAH C. Modeling fuzzy role based access control using fuzzy formal concept analysis [C]// Intel Symposium on Security in Computing and Communications. Kochi: Springer International Publishing, 2015, 536: 176-185.

[48] TANG Ya-qiang, FAN Min, LI Jin-hai. An information fusion technology for triadic decision contexts [J]. Intel Journal of Machine Learning and Cybernetics, 2016, 7(1): 13-24.

[49] POELMANS J, IGNATOV D I, KUZNETSOV S O, DEDENE G. Formal concept analysis in knowledge processing: A survey on applications [J]. Expert systems with applications, 2013, 40(16): 6538-6560.

[50] CH A K, DIAS S M, VIEIRA N J. Knowledge reduction in formal contexts using non-negative matrix factorization [J]. Mathematics and Computers in Simulation, 2015, 109: 46-63.

[51] KUMAR C A, ISHWARYA M S, LOO C K. Formal concept analysis approach to cognitive functionalities of bidirectional associative memory [J]. Biologically Inspired Cognitive Architectures, 2015, 12: 20-33.

[52] KUMAR C A. Fuzzy clustering-based formal concept analysis for association rules mining [J]. Applied Artificial Intelligence, 2012, 26(3): 274-301.

[53] BELOHLAVEK R, OSICKA P. Triadic concept lattices of data with graded attributes [J]. International Journal of General Systems, 2012, 41(2): 93-108.

[54] BELOHLAVEK R, OSICKA P. Triadic concept analysis of data with fuzzy attributes [C]// IEEE Intel Conference on Granular Computing (GrC). San Jose: IEEE Press, 2010: 661-665.

[55] BELOHLAVEK R, OSICKA P. Triadic fuzzy Galois connections as ordinary connections [J]. Fuzzy Sets and Systems, 2014, 249: 83-99.

[56] ZHUK R, IGNATOV D I, KONSTANTINOVA N. Concept learning from triadic data [C]// Intel Conference on Information Technology and Quantitative Management. Moscow: Procedia Computer Science, 2014, 31: 928-938.

[57] VOUTSADAKIS G. Polyadic concept analysis [J]. Order, 2002, 19(3): 295-304.

[58] TANG Ya-qiang, FAN Min, LI Jin-hai. Cognitive system model and approach to transformation of information granules under triadic formal concept analysis [J]. Journal of Shandong University (Natural Science), 2014, 49(8): 102-106.

[59] M. MAS development and its analysis based on FCA [R]. Ostrava-Poruba: Technical University of Ostrava.

[60] SHIVHARE R, CHERUKURI A K. Three-way conceptual approach for congnitive memory functionalities [J]. International Journal of Machine Learning and Cybernetics, 2016: 1-14.

(Edited by YANG Bing)

Received date: 2015-09-17; Accepted date: 2016-02-11

Corresponding author: Ch. Aswani Kumar; Tel: +91-4162202771; E-mail: cherukuri@acm.org