L(0,2)模态导波检测弯管缺陷的数值模拟和实验研究
罗更生1, 2，谭建平1，卢超3，郑明方4
(1. 中南大学 机电工程学院，湖南 长沙，410083；
2. 湖南省特种设备检验检测研究院，湖南 长沙，410111；
3. 南昌航空大学 测试与光电工程学院，江西 南昌，330063；
4. 北京工业大学 机械工程与应用电子技术学院，北京，100124)
摘要：针对低频超声导波纵向模态L(0,2)在弯管中传播的复杂性和对弯头典型部位缺陷检测的难度，目前尚未深入研究该模态在弯管处传播的能量分布特性和弯头拱背处典型缺陷的检测。采用数值模拟法分析L(0,2)模态在5种不同曲率半径钢制弯管中的传播特性，从波场快照研究信号能量分布变化，从时域波形研究模态转换；采用实验研究8根不同弯管弯头拱背外侧和内侧环向缺陷、过弯头后直管段缺陷的检测，对比分析L(0,2)模态的缺陷检出能力和模态转换特性。研究结果表明：L(0,2)模态经过弯管时，在弯头拱背外侧发生能量聚焦，该部位缺陷容易检出；在弯头拱背内侧发生信号衰减，导致该部位缺陷易漏检；过弯头以及弯头后直管段缺陷后均发生明显波形转换。研究结论为管道超声导波检测工程应用提供理论指导。
关键词：低频超声导波；L(0,2)模态；钢制弯管；波场快照；环向缺陷；模态转换
中图分类号：TP206+.1 文献标志码：A 文章编号：1672-7207(2014)09-3029-08
Numerical simulation and testing research for defect detection in bend pipes using longitudinal mode L(0,2)
LUO Gengsheng1, 2, TAN Jianping1, LU Chao3, ZHENG Mingfang4
(1. School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China;
2. Hunan Provincial Special Equipment Inspection and Research Institute, Changsha 410111, China;
3. School of Measuring and Optical Engineering, Nanchang Hangkong University, Nanchang 330063, China;
4. College of Mechanical Engineering and Applied Electronics Technology, Beijing University of Technology,
Beijing 1000124, China)
Abstract: Further study was needed to solve the problems about the spreading complexity of low-frequency ultrasonic guided wave longitudinal mode L(0,2) along the bend pipe and the difficulty of its defect detection of typical parts of bend’s extrados. Numerical simulation method was introduced to analyse spreading characteristic of mode L(0,2) in extrados of five steel bend pipes with different curve radius, in order to research energy distribution through snapshot and mode transition through time domain waveform. Defect detection and mode transition of mode L(0,2) were studied, through experiments of eight different bend pipes with circumferential defects in lateral and medial of bend’s extrados and in the straight part after bend. The results show that the energy of mode L(0,2) was focused on lateral part of bend’s extrados where the circumferential defect could be easily detected, but the opposite situation occured in medial of bend’s extrados; and obvious waveform transformation occured when mode L(0,2) spreaded along straight pipe after bend and the defect in straight pipe. In conclusion, this research provides a theoretical guidance for engineering applications of pipe’s defect detection using low-frequency ultrasonic guided wave.
Key words: low-frequency ultrasonic guided wave; longitudinal mode L(0,2); steel bend pipe; snapshot; circumferential defect; mode transition
钢管广泛应用于输送石油、天然气、化工原料、蒸汽等各种物资，与居民百姓生活息息相关。而弯管作为管道系统中不可或缺的一部分，在长期输送过程中极易受制造缺陷、管内介质冲刷腐蚀和管外第三方力量冲压等因素破坏，使管壁减薄或开裂，从而造成危险介质泄漏、爆炸等重大事故。因此，我国法律明确要求对其进行定期检验，以发现缺陷排除安全隐患。常规超声、漏磁、涡流等检测方法只能对管道进行点对点检测，检测速度慢[1]。而超声导波技术可在一个接触点实现长距离、全方位检测和评估管道中缺陷[1-2]，是目前研究的热点。超声导波信号经过弯管时传播特性复杂且会发生模态转换[3]，因此也是研究难点。L(0,2)模态为超声导波模态中的一种[4]，适应于检测管道环向缺陷[5]。Hayashi等[3]采用半有限元法分析L(0,2)模态经过弯头后的能量衰减率，并证明弯头造成的模态转换会延迟信号反射时间。Demma等[6]采用有限元方法分析了L(0,2)模态经过弯头时发生的模态转换。Demma[7]和Salley[8]采用有限元法分析了导波在弯管中的模态转换特性。Nishino等[9]使用宽带激光超声系统在弯管中激发导波，结合小波变换技术研究导波在弯管中的传播，发现L(0,1)模态在弯管中传播时发生模态转换出现F(1,1)模态。何存富等[1]采用有限元方法对单缺陷弯管和双缺陷弯管进行了数值计算，发现弯头缺陷的存在会影响弯头后直管段缺陷反射回波的幅度，并通过实验进行验证。王秀彦等[10-11]利用L(0,2)模态对90度弯管中的缺陷进行检测，分析了缺陷周向长度变化对缺陷回波和端面回波幅值大小的影响等。但上述文献未深入研究L(0,2)模态在弯头中传播时发生的能量分布特性，以及L(0,2)模态检测弯管拱背处典型位置环向缺陷的能力。本文作者采用数值模拟法分析L(0,2)模态在5种不同曲率半径钢制弯管中的传播特性，从波场快照研究信号能量分布变化，从时域波形研究模态转换；采用实验研究8根不同弯管弯头拱背外侧和内侧环向缺陷、过弯头后直管段缺陷的检测，对比分析L(0,2)模态的缺陷检出能力和模态转换特性。为管道超声导波检测的工程应用提供理论指导。
1 基本理论
根据弹性波理论和图1所示的圆柱坐标系，可以建立超声导波在空心圆柱管中传播时的质点位移方 程[4, 12-13]：
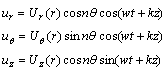(1)
式中：
，
和
分别为径向、周向和轴向位移分量；
，
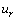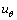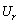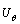和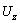
分别为由Bessel函数构成的径向、周向和轴向位移幅度；周向阶次n=0, 1, 2, 3, …；w为角频率；k为波数。
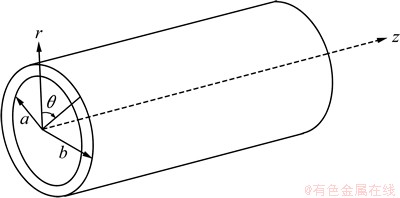
图1 圆柱坐标系
Fig. 1 Cylindrical coordinate system
超声导波在管道中传播时存在3种不同模态，即纵向(轴对称)模态L(0,m)、扭转(轴对称)模态T(0,m)和弯曲(非轴对称)模态F(n,m)，其中模数m=1, 2, 3, …。当n=0时对应于轴对称模态，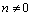
对应非轴对称模态。
根据线弹性理论，可以得到空心圆柱管中超声导波轴对称模态的频散方程[14]：
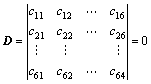(2)
式中：函数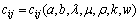
；a和b分别为管子内径和外径；
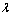和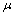
为材料的Lames常数；
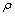为材料密度。
由频散方程可以得到轴对称模态的相速度和群速度频散曲线， 根据频散曲线可以看出各模态的频散特性，为选择检测管道缺陷的导波信号提供依据。
2 L(0,2)模态检测弯管的数值模拟
2.1 数值模型
本文用ABAQUS/Explicit瞬态动力分析模块建立弯管超声导波L(0,2)模态传播的数值模型，该模型选用六面体网格、3D实体模型和C3D8单元类型，如图2所示。钢管模型外径×壁厚×长度为159 mm×4.5 mm×1 800 mm，材质为碳钢，其弹性模量E=210 GPa、密度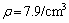
、泊松比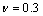
。“端A”为信号激励端；“端B”为钢管末端；“面C”为反射导波监测面，主要是验证激励信号和分析从弯管弯头处反射回来的信号；“面D”为透射导波监测面，主要是提取透射信号。
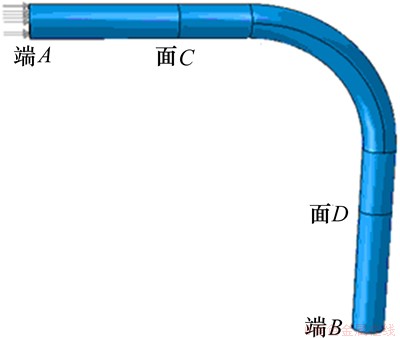
图2 弯管导波检测的数值模型
Fig. 2 Bend pipe model used in FE simulation
“端A”加载文献[15]所示的经过汉宁窗调制的余弦信号：
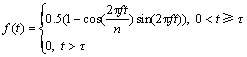(3)
式中：n为脉冲周期；f为中心频率；
为信号脉冲宽度。
根据式(2)计算得到图3所示的159 mm×4.5 mm (外径×壁厚)钢管的相速度频散曲线。从频散曲线可以发现，L(0,2)模态的相速度在40~100 kHz范围内是非频散的。仿真分析时取f=40~100 kHz，扫描步进取10 kHz；脉冲周期n=5。
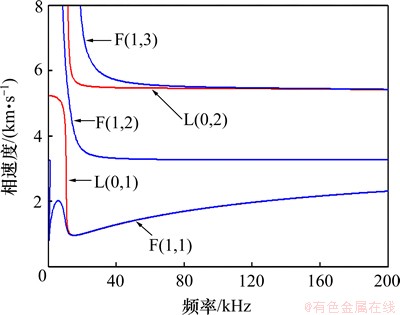
图3 159 mm×4.5 mm(外径×壁厚)钢管的相速度频散曲线
Fig. 3 Phase velocity dispersion curves for the carbon steel pipe (159 mm outer radius, 4.5 mm wall thickness)
2.2 仿真分析
根据图2所示的数学模型，分析L(0,2)模态在曲率半径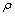=2D，4D，6D，8D，10D(D为管子外径)弯管中的传播。L(0,2)模态在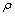=2D弯管传播过程中的波场快照如图4所示。由图4可以看出：1) 导波在弯头部位的波结构与直管部位明显不同，L(0,2)模态途经弯头部位时的导波能量聚焦在拱背外侧，在最外侧能量最强。而拱背内侧的能量大大减弱，在最内侧能量几乎消失。2) L(0,2)模态穿过弯头部位再次到达直管部位时，其模态结构又恢复与激励端的入射模态一致，但信号变长。L(0,2)模态在直管和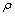=2D，4D，6D，8D，10D弯头中传播时的波场快照如图5所示，得到同样规律。
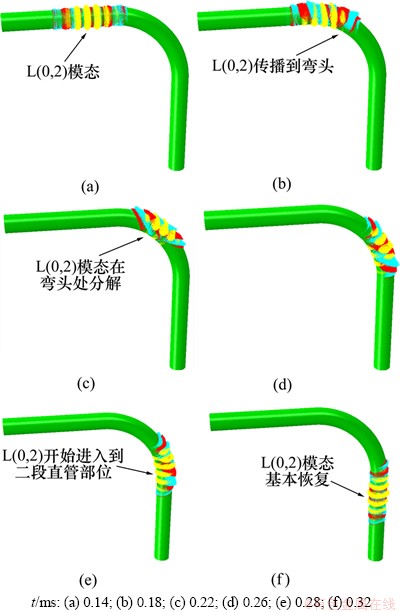
图4 L(0,2)模态在ρ=2D弯管传播过程中的波场快照
Fig. 4 Snapshots of L(0,2) mode propagation through bend pipe (ρ=2D) at different time points
此外，为了观察L(0,2)模态经过弯头后的模态转换特性，在“面C”、“面D”处分别监测激励信号、经过弯头后的透射信号的时域波形，如图6所示(弯头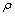=4D)。可以发现：L(0,2)模态经弯头后转换出F(1,3)和F(2,3)模态，两者均为非轴对称的弯曲模态，会对缺陷的检测产生较大干扰。
3 实验研究
为验证数值模拟结果，制作了8根含缺陷弯管试样进行超声导波检测实验，弯管试样技术参数如表1所示。其中，弯管规格和缺陷加工示意图如图7所示，缺陷为环向缺陷、半月牙形，缺陷尺寸是指缺陷横截面积与缺陷处管壁横截面积之比；直管段加工缺陷的目的为验证L(0,2)模态经过弯头后检测缺陷的能力。
实验设备采用英国Plant Integrity公司生产的Teletest Focus低频超声导波检测系统，该系统由主机、电源、卡具、气囊、多模式模块和软件等部件组成。信号采集时，通过卡具将传感器固定在弯管上2.5 m直管段的端部，如图8所示。
实验时，L(0,2)模态导波频率范围为40~100 kHz，步进为10 kHz；脉冲周期n=5，10，15，20。实验测试结果如表2所示，有效验证了数值模拟结论。测试结果中只列举了2张检测波形图进行简要分析(图9和10)，具体如下：
1) L(0,2)模态导波在特定的信号频率和脉冲周期下，能有效检测出弯头拱背外侧和过弯头直管段缺陷，但拱背外侧缺陷回波与弯头两端环焊缝回波有重叠，L(0,2)模态导波过弯头以及弯头后直管段缺陷后都发生波形转换。随着弯头上缺陷尺寸的增加，缺陷反射回波幅度逐渐增加、与环焊缝回波重叠区域逐渐减小，与此同时，过弯头后直管段缺陷反射回波和管端反射回波逐渐下降，且两回波逐渐重叠。
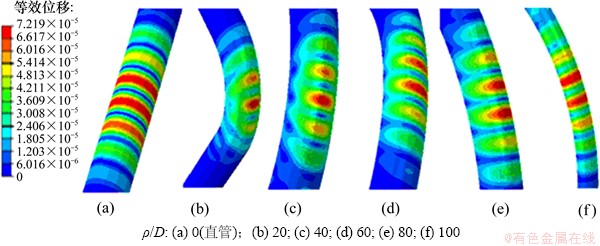
图5 L(0,2)模态在直管和不同弯曲曲率半径弯头处传播时的波场快照
Fig. 5 Snapshots of L(0,2) mode propagation through straight pipe and pipe bends with different curvature radius
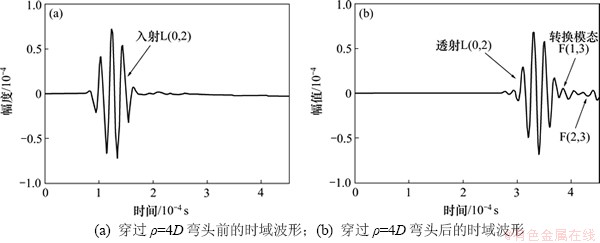
图6 L(0,2)模态在穿过ρ=4D弯头前后的时域信号
Fig. 6 Time trace of waves measured when L(0,2) mode traveling before bend (ρ=4D) and after bend respectively
表1 含缺陷弯管试样技术参数
Table 1 Technical parameters of bend pipes with defects used in experiment
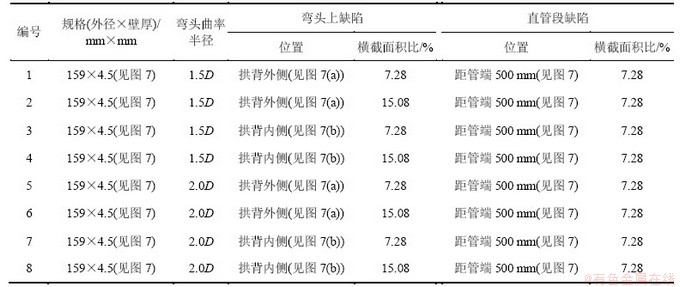
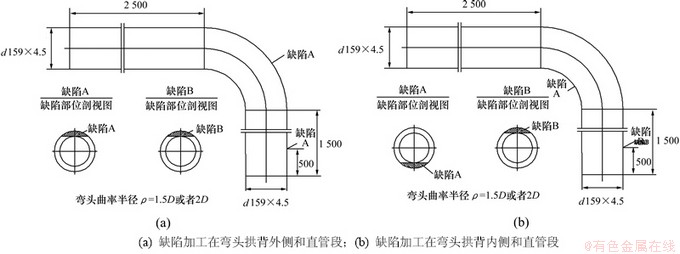
图7 弯管规格和缺陷加工示意图(单位：mm)
Fig. 7 Layout of bend pipes used in experiment
图8 实验系统及现场
Fig. 8 Experiment set-up
2) L(0,2)模态导波无法有效检出弯头拱背内侧缺陷，即使缺陷尺寸逐渐增大。但L(0,2)模态导波能检出过弯头后直管段缺陷，缺陷反射回波后面出现波形转换波。但随着拱背内侧缺陷尺寸的增大，直管段缺陷反射回波幅度没有明显变化。
3) 借助反射回波时域波形对应的能谱图能有效辨别出缺陷、焊缝、管端等各种结构变化的反射回波，并对其定位。尤其是各反射回波信号微弱或互相重叠时，能谱图的作用效果非常明显。能谱图不同颜色区域代表不同强度的反射信号，红色、黄色、绿色、蓝色代表信号强度依次由强到弱，红色和黄色一般代表缺陷、焊缝、管端等各种结构变化的反射回波。
表2 实验测试结果
Table 2 Experimental results
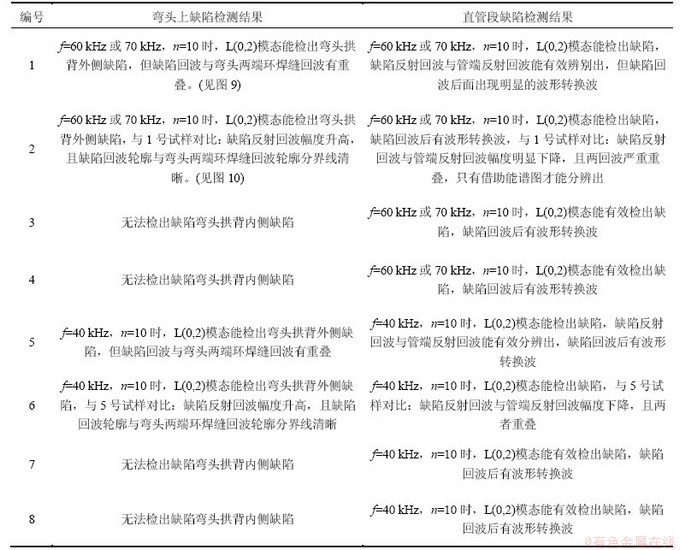
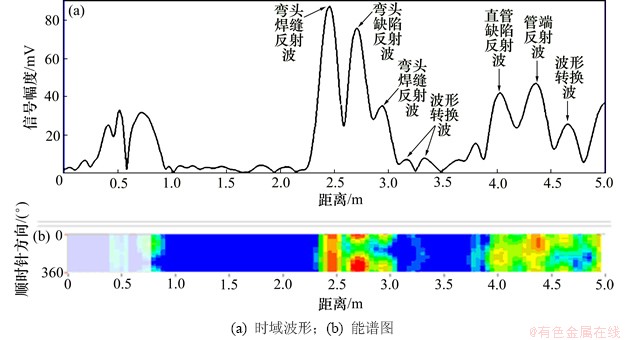
图9 f=60 kHz，n=10时，L(0,2)模态检测1号弯管结果(弯头拱背外侧缺陷横截面积比为7.28%)
Fig. 9 Experimentally measured waves when incident L(0,2) mode (at 60 kHz central frequency, 10 signal cycle) propagation through No.1 pipe with defect (cross-sectional area ratio is 7.28%) in extrados of bend
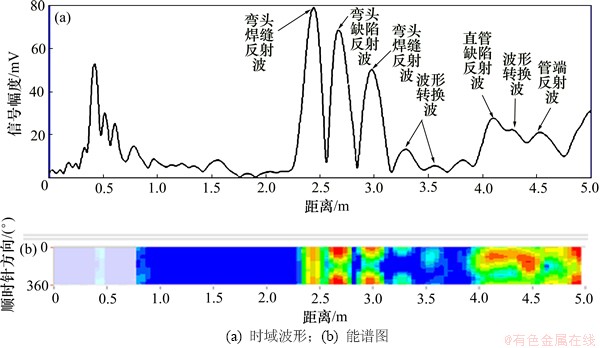
图10 f=70 kHz，n=10时，L(0,2)模态检测2号弯管结果(弯头拱背外侧缺陷横截面积比为15.08%)
Fig. 10 Experimentally measured waves when incident L(0,2) mode (at 70 kHz central frequency, 10 signal cycle) propagation through No.2 pipe with defect (cross-sectional area ratio is 15.08%) in extrados of bend
4 结论
1) L(0,2)模态经过弯头时会在拱背外侧产生能量聚焦，在拱背最外侧能量最集中；在拱背内侧能量发散，拱背最内侧信号几乎消失。因此，L(0,2)模态能检出弯头拱背外侧环向缺陷，无法检出弯头拱背内侧缺陷，而且随着弯头缺陷尺寸的增加，缺陷更易被检出，但过弯头后直管段缺陷反射回波幅度却逐渐减弱，与管端反射回波逐渐重合，借助能谱图才能有效辨别信号。
2) L(0,2)模态经过弯头以及弯头后的直管段缺陷后均发生波形转换。转换波为非轴对称的弯曲模态，对缺陷检测产生不利影响。
3) 弯头拱背外侧或内侧存在一环向缺陷时，L(0,2)模态也能有效检出经过一个弯头后的直管上环向缺陷。
4) 进行有限元分析时，波场快照能快速有效看出L(0,2)模态在弯头处的能量变化特性。进行导波检测时，反射回波时域波形对应的能谱图能有效辨别出缺陷、焊缝、管端等各种结构变化的反射回波。波场快照和能谱图是进行超声导波检测分析时非常实用的2种技术工具。
参考文献：
[1] 何存富, 孙雅欣, 刘增华, 等. 弯管缺陷超声导波检测的有限元分析[J]. 北京工业大学学报, 2006, 32(4): 290-294.
HE Cunfu, SUN Yaxin, LIU Zenghua, et al. Finite element analysis of defect detection in curved pipies using ultrasonic guided waves[J]. Journal of Beijing University of Technology, 2006, 32(4): 290-294.
[2] 李一博, 靳世久, 孙立英. 超声导波在管道中的传播特性的研究[J]. 电子测量与仪器学报, 2005, 19(5): 63-66, 89.
LI Yibo, JIN Shijiu, SUN Liying. Study on propagation characteristic of ultrasonic guided waves along the pipe[J]. Journal of Electronic Measurement and Instrument, 2005, 19(5): 63-66, 89.
[3] Hayashi T, Kawashima K, SUN Zongqi, et al. Guided wave propagation mechanics across a pipe elbow[J]. Journal of Pressure Vessel Technology, 2005, 127: 322-327.
[4] Rose J L. 固体中的超声波[M]. 何存富, 吴斌, 王秀彦, 译. 北京: 科学出版社, 2004: 128.
Rose J L. Ultrasonic waves in solid media[M]. HE Cunfu, WU Bin, WANG Xiuyan, translated. Beijing: Science Press, 2004: 128.
[5] 宋志东. 超声导波技术在管道缺陷检测中的研究[D]. 天津: 天津大学, 2006: 47-48.
SONG Zhidong. Research on defect detection in pipies using ultrasonic guided waves[D]. Tianjing: Tianjing University, 2006: 47-48.
[6] Demma A, Cawley P, Lowe M, et al. The effect of bends on the propagation of guided waves in pipes[J]. Journal of Pressure Vessel Technology, 2005, 127: 328-335.
[7] Demma A, Cawley P, Lowe M J S, et al. Mode conversion of longitudinal and torsional guided modes due to pipe bends[J]. Review of Progress in Quantitative Nondestructive Evaluation, 2001, 20: 172-179.
[8] Salley L, PAN Jie. A study of the modal characteristics of curved pipes[J]. Applied Acoustics, 2002, 63: 189-202.
[9] Nishino H, Yoshida K, Cho H, et al. Propagation phenomena of wideband guided waves in a bended pipe[J]. Ultrasonics, 2006(44): 1139-1143.
[10] 王秀彦, 刘增华, 孙雅欣, 等. 弯管中超声导波传播特性的研究[J]. 北京工业大学学报, 2006, 32(9): 773-777.
WANG Xiuyan, LIU Zenghua, SUN Yaxin, et al. Research on the propagation characteristics of ultrasonic guided waves in curved pipes[J]. Journal of Beijing University of Technology, 2006, 32(9): 773-777.
[11] 王秀彦, 王智, 焦敬品, 等. 超声导波在管中传播的理论分析与实验研究[J]. 机械工程学报, 2004, 40(1): 11-16.
WANG Xiuyan, WANG Zhi, JIAO Jingpin. Theoretical and experimental studies of ultrasonic guided waves propagation in pipes[J]. Chinese Journal of Mechanical Engineering, 2004, 40(1): 11-16.
[12] ZHENG Mingfang, LU Chao, CHEN Guozhu, et al. Modeling three-dimensional ultrasonic guided wave propagation and scattering in circular cylindrical structures using finite element approach[C]// 1st International Conference on Physics Science and Technology. Netherlands: Physics Procedia, 2011: 112-118.
[13] Achenbach J D. 弹性固体中波的传播[M]. 徐植信, 洪锦如, 译. 上海: 同济大学出版社, 1992.
Achenbach J D. Wave propagation in elastic solids[M]. XU Zhixin, HONG Jinru, trans. Shanghai: Tongji University Press, 1992.
[14] Gazis D C. Three-dimensional investigation of the propagation of waves in hollow circular cylinders. Ⅰ. Analytical foundation, Ⅱ. Numerical results[J]. J Acoust Soc Am, 1959, 31(5): 568-578.
[15] LU Chao, XIA Longyu, ZHENG Mingfang. 3-D numerical modeling of ultrasonic guided wave testing for defect in rock bolt[C]// 2nd International Conference on Materials Engineering for Advanced Technologies. Germany: Advanced Materials Research, 2013: 794-800.
(编辑 陈爱华)
收稿日期：2013-12-08；修回日期：2014-03-26
基金项目：国家自然科学基金资助项目(E051102)；湖南省科技计划项目(2013TT2028)；国家质检总局科技计划项目(2012QK162)
通信作者：谭建平(1963-)，男，湖南攸县人，教授，博士生导师，从事现代机电液控制理论与技术、机电系统状态监测故障诊断、微型流体机械设计与驱动控制研究；电话：13607311991；E-mail: jptan@163.com
