Numerical investigation of flow pattern and components of three-dimensional velocity around a submerged T-shaped spur dike in a 90° bend
来源期刊:中南大学学报(英文版)2016年第11期
论文作者:Mohammad Vaghefi Yaser Safarpoor Maryam Akbari
文章页码:2984 - 2998
Key words:T-shaped spur dike; flow pattern; submergence ratio; SSIIM model
Abstract: Spur dike is one of the river training structures. This work presented a numerical simulation of flow field and three-dimensional velocity around a T-shaped spur dike located in bend using SSIIM model. The main objective of this work is to investigate the three-dimensional velocities and streamlines at transverse and longitudinal sections and plan views around the T-shaped spur dike in different submergence ratios (0, 5%, 15%, 25% and 50%). It is concluded that by increasing the submergence ratio from 5% to 50%, the maximum of scour is reduced; the maximum of longitudinal velocity increases by 7.7% and occurs at the water surface in spur dike axis. Near the bed, the maximum of vertical velocity occurs at the end of spur wing. By analyzing the streamlines at transverse sections, the followings were deduced for different submergence ratios: different dimensions and different positions of vortices around the spur dike.
J. Cent. South Univ. (2016) 23: 2984-2998
DOI: 10.1007/s11771-016-3362-z
Mohammad Vaghefi, Yaser Safarpoor, Maryam Akbari
Department of Civil Engineering, Persian Gulf University, Shahid Mahini Street,P.O. Box: 75169-13817, Bushehr, Iran
 Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Abstract: Spur dike is one of the river training structures. This work presented a numerical simulation of flow field and three-dimensional velocity around a T-shaped spur dike located in bend using SSIIM model. The main objective of this work is to investigate the three-dimensional velocities and streamlines at transverse and longitudinal sections and plan views around the T-shaped spur dike in different submergence ratios (0, 5%, 15%, 25% and 50%). It is concluded that by increasing the submergence ratio from 5% to 50%, the maximum of scour is reduced; the maximum of longitudinal velocity increases by 7.7% and occurs at the water surface in spur dike axis. Near the bed, the maximum of vertical velocity occurs at the end of spur wing. By analyzing the streamlines at transverse sections, the followings were deduced for different submergence ratios: different dimensions and different positions of vortices around the spur dike.
Key words: T-shaped spur dike; flow pattern; submergence ratio; SSIIM model
1 Introduction
Spur dikes are hydraulic engineering structures for preserving the desired water depth, deflecting the main current in the harbor channels and rivers, and protecting river banks. Since the past, spur dikes have been used as an economical way to protect the river banks in their outer banks. For this reason, many researchers have studied the flow pattern and scours around the spur dikes located in the bend and straight routs of rivers. Blanckaert and Graf [1] did an experimental study on a bend channel and measured secondary flow and maximum velocity. Booij [2] using large eddy simulation (LES) simulated flow field in a 180° bend and measured Reynolds shear stress. Vaghefi et al [3] studied experimentally the effect of streamlines variations, the maximum velocity distribution, and the secondary flow strength on bed shear stress distribution along a 180° sharp bend. Naji et al [4] experimentally and numerically studied flow pattern in a 90° bend and concluded that stream lines in the level close to bed orient to inner wall and in the levels near water surface orient to outer wall. Also, the location of the maximum longitudinal velocity at the beginning of the bend is switched to the inner half and then toward outer wall.
Zhu and Liu [5] studied the local scour hole around a cylindrical bridge pier by a CFD model. In this numerical method, the time-averaged Reynolds- Navier-Stokes equations and the standard k-ε model were first used to simulate the three-dimensional flow field around a bridge pier fixed on river bed. The transient shear stress on river bed was treated as a crucial hydrodynamic mechanism when handling sediment incipience and transport. Then, river-bed volumetric sediment transport was calculated. Rajaratnam and Nwachukwu [6-7] studied the structure of turbulent flow near groin based on experimental observations. Giri et al [8] carried out experimental and numerical simulations of flow and turbulence in a bend channel with non-submerged spur dikes. They measured flow velocity by changing the position of spur dikes, and measured vortex field and turbulence intensity two-dimensionally. Nagata et al [9] carried out a numerical simulation of three-dimensional flow pattern around a single spur dike with live bed; they analyzed average flow and studied its relation with the way scour hole created and expanded. Fazli et al [10] did an experimental study on a 90° bend channel to study the parameters affecting scour around short and straight spur dikes. The results indicate that in developed bends, as the spur dike is moved away from the beginning of the bend, the maximum depth of scour rises. Zhang et al [11] investigated turbulent flow in the local scour hole around a single non-submerged spur dike experimentally and numerically. They measured the scour geometry and flow velocities in details with a high-resolution laser displacement meter, electro-magnetic velocimeter and PIV (particle image velocimetry). Moreover, they used a 3D non-linear k-ε model to simulate the complex local flow field around the scour area. Duan et al [12] investigated average and turbulent flow around a straight spur dike located in channel with rigid bed. They observed that in the circulation zone behind the spur dike, there is a combination of horizontal and vertical vortexes. Flow field passing through a spur dike is characterized with the separation of approaching flow in three dimensions (3D) from upstream to the horseshoe vortex downstream of the dike. The complexity of flow field increases as the scour hole develops. Duan et al [13] measured three-dimensional flow field around a dike structure using a micro ADV. They studied turbulent bursts around the spur dike for the flat and asymptotic bed surface. Gu et al [14] performed the laboratory experiments to study the characteristics of the flow and the transport of suspended sediment in an open channel with permeable dikes. They investigated the influence of the aspect ratio of the interval between dikes to the length of dikes on these characteristics. Chen et al [15] used the compressive VOF (volume of fluid) method to develop the models for water and suspended sediment in a 90° bend flume with non-submerged spur dike at different angles. They simulated local scouring, deposition and re-suspension, and analyzed the processes of adsorption and desorption of pollutants on suspended sediment. Sharma et al [16] studied experimentally the flow past a spur dike on a rigid bed meandering channel with a trapezoidal cross section. Their results showed that length of the downstream separation zone changes according to the location of the spur dike.
Fang et al [17] studied the turbulent flow past a series of groins in a shallow, open channel by large-eddy simulation (LES). Their results showed that a rectangular-headed groin generates higher turbulence intensities and larger vortices than a round-headed groin. Mccoy et al [18] investigated flow pattern around and between two spur dikes in an open channel. Gill [19] in an experiment proved that the distance between spur dikes depends much on the radius of curvature. In nearly straight routes, the distance between spur dikes is about 5 times the length of the spur dike, whereas in bends it is equal to or twice the length of the spur dike. Acharya and Duan [20] carried out a three-dimensional numerical investigation of turbulent flow pattern around series of straight spur dikes located in a straight route with live and fixed bed. They used k-ε turbulence model for modeling, and compared the results with experimental results.
Ghodsian and Vaghefi [21] carried out an experimental study on how changes in Froude Number and length of wing and web of T-shaped spur dike in a 90° bend; They proved that as the length of the spur dike increases, the length of separation zone and the formed vortex in the zone increases. Vaghefi et al [22-25] placed the T-shaped spur dike in a 90° bend, and carried out several experimental studies on the effects of the Froude Number, the length of the spur dike, the position of the spur dike, the radius of curvature, etc. They concluded that the location of the maximum scour depth is at the distance of 10% to 20 % of spur length and at its upstream. They also observed that increasing the length of the spur dike, decreasing the length of the wing of the spur dike, increasing Froude Number, and positioning the spur dike towards downstream will result in an increase in the dimensions of the scour hole. In submerged spur dike, the results indicated that in cross section around the submerged spur dike, when Froude number increases, the formed vortexes decreased by 35%. Vaghefi et al [26-28] numerically investigated effect of submergence percentage on the flow pattern around the T-shaped spur dike at a 90° bend and concluded that by increasing spur submergence near the inner wall the longitudinal velocity is reduced to half of the main velocity. To evaluate the effect of the submerged T-shaped spur dike on water surface profiles, they numerically simulated the flow around the submerged spur dike in a 90° bend. The results of their modeling showed that in different states, due to the secondary flows and centrifugal force in the mild bend, the flow leans toward the outer bank and thus the maximum increase of water level occurs in the outer bank and at the spur dike upstream. Also they showed that the SSIIM model acts good in 90° channel bend with movable bed. Vaghefi et al [29] studied the effect of support structure on flow patterns around T-shaped spur dike in 90° bend channel numerically. They concluded that by increasing support structure distance, the power of secondary flow around main spur dike decreases and the length of separation zone increases.
The spur dike structures due to variations in shape and performance have been studying over the years by different researchers. But the main argument in this research is the study of T-shaped spur dikes that due to a cross section in the tip of the spur dike (spur dike wing), it has a unique impact on the flow pattern. On the other hand, the spur dikes during its operation are submerged due to the current fluctuations or river flooding. So, it is important to analyze the spur dike in submerged mode. As it is mentioned, the study and investigation of the flow and scour around the submerged spur dike located in the bend has been very limited. The main objective of this work is to investigate the three-dimensional velocity components around the T-shaped spur dike located in the 90° bend with a mobile bed using SSIIM model (version-1), while considering different percentages of submergence. For this reason, first, the results of numerical modeling have been compared with experimental results and then three-dimensional velocity components, streamlines as various longitudinal and transverse sections and plan views have been investigated and analyzed for different states.
2 Material and methods
2.1 Experimental setup and measurements
The experiments have been carried out by Vaghefi et al [30] in Hydraulics Laboratory of Tarbiat Modares University in Iran, on a laboratory flume as shown in Fig. 1 with the width of 60 cm, and the height of 70 cm, in a compound of direct and bend routes. The straight upstream route is 710 cm in length, and is connected to straight downstream route of 520 cm length via a 90° bend with an external radius of 270 cm, and an internal radius of 210 cm. The ratio of bend radius to width of channel is 4. Uniform sediments have an average diameter of 1.28 mm and standard deviation is 1.3; also the flow discharge throughout the experiment is held constant, and equals 25 L/s. The flow depth is equal to 11.6 cm at the entrance of the bend. Accordingly, the Froude number is also equal to 0.34 in the upstream straight rout. The flow measurement is done by the Vectrino velocimeter at different radial sections and for several horizontal layers. The velocity at each point is measured by sampling rate of 50 Hz for a period of 1-3 min and time average values were calculated. The spur dike used in these experiments is a T-shaped plexiglas spur dike. The length of wing and that of web are the same and equal to 9 cm, with the height of 25 cm. This spur dike is vertical and non-submerged in a 45° position, and is located in the external bend.
2.2 Numerical modeling
SSIIM is abbreviation for sediment simulation in intakes with multiblock option. This program is made for river, environmental, hydraulic and sedimentation engineering. The main motivation for creating the program by Olsen [31], was to simulate the sediment movements in general river geometries. It has been shown to be difficult to do in physical model studies for fine sediments. The SSIIM program solves the Navier-Stokes equations with the k-ε model on a three-dimensional almost general non-orthogonal grid. A control volume method is used for the discretization, together with the power-law scheme or second order upwind scheme. The SIMPLE method is used for the pressure coupling. An implicit solver is used, producing the velocity field in the geometry. The velocities are used when solving the convience-diffusion equations for different sediment sizes. To calculate Reynolds stress term, SSIIM uses the k-ε model. Therefore, kinetic energy of the turbulent flow model is characterized based on the flow velocity. The cinematic viscosity is the fluid properties while the eddy viscosity depends on the velocity and is expressed to introduce the Reynolds stress [31-33]. The flow field for three-dimensional geometry is determined by solving the continuity equation and the Reynolds averaged Navier-Stokes equations [34-35].
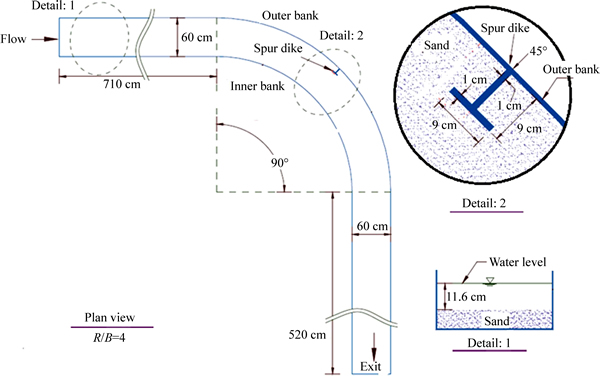
Fig. 1 Laboratory channel plan view
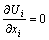 (1)
(1)
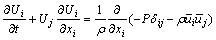 (2)
(2)
where U is the velocity averaged over the time t; x is the spatial geometrical scale; ρ is the water density; p is the pressure; δ is the Kronecker delta; and u is the velocity fluctuation over time during time step Δt. The discretization method was based on a finite volume approach. The Reynolds stress term was modeled by the k-ε turbulence model. The SSIIM model computes the turbulent stresses, using the eddy viscosity relation:
 (3)
(3)
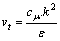 (4)
(4)
where υt is coefficient; k is the turbulent kinetic energy and ε is its dissipation rate determining the eddy viscosity υt, obtained from the following equations:
 (5)
(5)
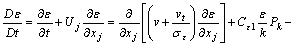
 (6)
(6)
The SIMPLE method was used to compute the pressure. A second-order upwind scheme was used for the discretization of the convective terms. The Rhie and Chow interpolation was applied to compute the velocities and the fluxes at the cell surfaces. Zero gradient boundary condition was used for all variables at the outflow boundary. The upstream velocities defined by Dirichlet boundary conditions. Wall law function for rough boundary was used for the side walls and the bed.
2.3 Model validation
In this work, different turbulence models were used for calibrating of software. These models are expected in SSIIM that will be introduced in the control file. It was observed that the k-ε model is close to the experimental results, and so all calculations were performed using the k-ε model. Various models that have been used are as follows: standard k-ε model, k-ε model with some RNG extensions and k-ω (k-omega) model. Roughness parameters are needed for SSIIM for two purposes: generation of the initial water surface elevation and computation of the shear stress at the boundaries. The bed and wall roughness is chosen as a constant Strickler value, kst=64 m1/3/s. The preparation of the optimal grid in numerical model is very important. Since SSIIM (version-1) software is not able to produce the required grid for modeling, the Matlab software has been used to generate it. In order to achieve better and more detailed results, finer grid has been used in the areas around the spur dike and coarser grid for the areas away from it. In this study, after extensive investigation, optimum grid was considered 75 in width, 33 in length, and 20 in depth (75×33×20). The grid system was defined according to the distortion ratio. The distortion ratio should not be too great. The distortion ratio is the dimension of the grid in one direction divided by the dimension in another direction. In channel upstream, the mentioned ratio is equal to 4 (because the bed’s changes is small in this area); in around spurs and channel downstream it is equal to 2 and 3, respectively. The grid system was checked using a finer mesh, where the gridlines were doubled in longitudinal lateral and directions. In this case the computation time is very long whereas the results of two models are equal with close approximation. The grid size is small enough to minimize errors from dissipation due to grid. In SSIIM-1 several sediment transport formulas are used to calculate the concentration at the bed, such as van Rij’n and Einstein’s bed load formula or Ackers/White’s formula [36-38]. In this study, the changes in the bed topography using the van Rij’n formula, agrees more with the laboratory results. The sediment transport calculation is transient; therefore, a time step should introduce. The time step chooses 20 s; this time must not be so large that the changes in bed topography cause the flow pattern change significantly [39]. Also in this work, we used the less time similar to 18, but only increased the computing time and the results did not change. In order to verify the results of the numerical modeling, they are compared with the results of experimental model under the same conditions. In Figs. 2 and 3, comparisons of the bed profiles at different cross sections (at distances of 0.7 times the length of the spur at upstream (section of 43.75°) and 0.54 times that at downstream) are shown. As can be seen, the maximum scour and main scour hole occur in the spur dike upstream.
In addition, it is evident that from the bend's external wall to the spur dike location, the numerical and experimental results are more consistent than spur dike downstream because due to sedimentation phenomena, more complex topography changes are observed at downstream. As expected, the maximum scour for both numerical and experimental models in Fig. 2 occurs in the outer bank. Vertical and longitudinal velocities at 43.75° cross-section and longitudinal-section are illustrated in Fig. 3. Figure 3(a) shows the transverse section near the spur dike upstream. It is seen that vertical velocity has been higher when reaching to the outer bank and around the spur dike, the reason of which is blocking the flow by installation of spur dike and forcing it to move along the spur dike, vertically toward the bed.
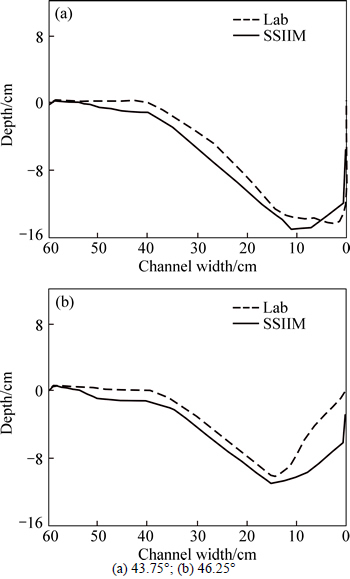
Fig. 2 Cross profile of models:
In Fig. 3(b), it is also seen that the longitudinal components of flow's velocity have been minimum both in numerical and experimental models near the bed, and on the way from the bed to water level, the velocities increase due to the loss of boundary layer. From a comparison of Figs. 2 and 3, it can be concluded that numerical and experimental results are in good agreement and the numerical model of SSIIM has high capacity to simulate the flow and sediment in curved paths with hydraulic structures such as spur dikes.
3 Results and discussion
In Fig. 4, the sample of submerged spur dike is shown and the submergence ration has been described. The order of percentage of submergence is the ratio of “h1/H” where “h1” is the distance of spur dike crest level to the water level and “H” is the water depth.
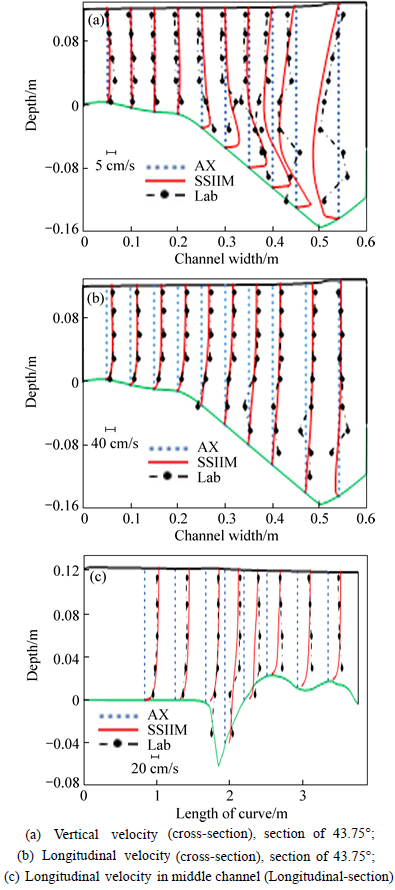
Fig. 3 Comparison of velocities:
3.1 Transverse velocity (Ur)
By spur dike submergence, the maximum transverse velocity )toward outer bank) occurs in section 47.5° at downstream of spur dike within 10% distance of the channel width from outer bank and 5% distance of flow depth from the bed. However, the maximum flow velocity toward the inner bank occurs in section 44.9° at upstream of the spur dike and outside its wing within 15% of the channel width from the outer bank and in total, it decreases by increasing the submergence ratio. In Fig. 5, three cross-sections at downstream and upstream of the spur dike namely section 43.75° at upstream of spur dike wing (section within 0.7 times the length of the spur dike from the spur dike toward upstream) and section 44.5° (section within 0.3 times the length of the spur dike from the spur dike toward upstream) and section 46.25° in downstream of spur dike wing (section within 0.6 times the length of spur dike from the spur dike toward downstream) have been shown, whose transverse velocities and the bed profile have been patched and compared with each other in different submergence ratios. The first observation relates to the bed profile that by increasing the submergence ratio, the scour is reduced but the changes of velocity are not significant, and there is no obvious change in transverse velocities quantity. We see that transverse velocities in the upstream of the spur dike are a bit more than velocities in the downstream of spur dike that somehow show greater strength of the secondary flow at upstream of the spur dike. The velocity increases from inner bank to spur location and decreases when reaching spur dike or outer bank In caused by the effect of spur dike on the flow pattern. As Figs. 5(a) and (b), it is understood that near the outer bank, due to the flow separation zone in spur upstream, the flow direction is toward the inner bank. Also in Fig. 5(c), the changes of velocity direction near the outer bank show reattachment zone and creation of vortices. By comparing the latter, the width of separation zone is greater than the reattachment zone.
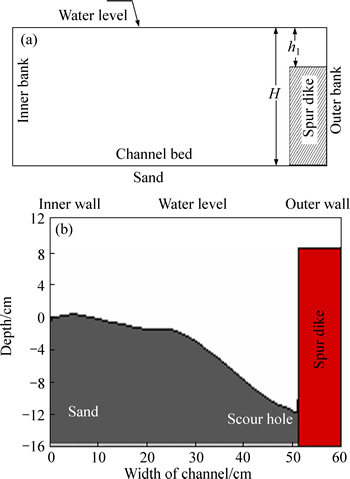
Fig. 4 Cross section of model in submerged spur dike case inner (a) and outer banks (b) scour hole
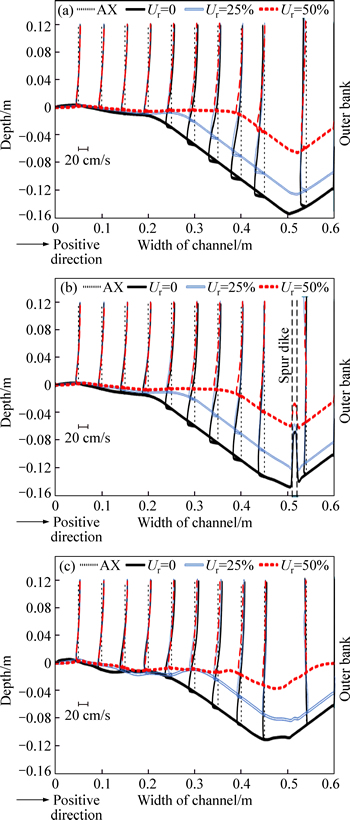
Fig. 5 Transverse velocity at cross sections of 43.75° (a), 44.5° (b) and 46.25°(c)
3.2 Longitudinal velocity (Vteta)
In the case of spur dike submergence and by increasing submergence ratio, the maximum of longitudinal velocity according to Table 1, increases slightly and its maximum occurs at the water surface in spur dike axis. On the other hand, according to Table 2, the maximum of longitudinal velocity approaches the outer bank by increasing submergence ratio. In Fig. 6, the longitudinal velocities were checked in different submergence ratios in sections of upstream and downstream of spur dike. Like the transverse velocity,quantity and changes of velocity are not so different by changing the submergence ratio. The longitudinal velocity was reduced in scour holes.
Table 1 Distance of the maximum longitudinal velocity from outer bank based on submergence ratio

Table 2 Increase of the maximum longitudinal velocity based on submergence ratio

Figure 6(a) and (b) show that within a distance of 10% of the channel width from outer bank (within 6 cm from the outer bank and in the spur upstream), the longitudinal velocity is negative at lower depths, which indicates creation of vortexes in longitudinal section of the channel. This longitudinal vortex is formed duo to installing the spur dike and the formation of the downward flow.
In Fig. 6(c), the longitudinal velocity (within 10% distance of the channel width from the outer bank) is very low in spur field, that is a part of recirculation flow area, which indicates the protected area with less changes, but by increasing the submergence ratio, due to passing of flow over the spur crest, the longitudinal velocity increases at upstream and downstream sections and even at the spur dike axis section. So, lower scour occurs at spur upstream and the changes of bed topography decrease.
In Fig. 7, the same sections of Figs. 6(b)-(c) are shown magnified (at distance of 40 to 60 cm from the inner bank) near the outer bank. In Fig. 7(a), because of the spur dike, it is seen that the longitudinal velocities are very low until to spur crest level, whereas by passing flow from the spur crest, the longitudinal velocities by increasing of the submergence ratio become greater. Also, Fig. 7(b) shows that the longitudinal velocities near the spur axis and near the bed are negative, which indicates flow movement toward upstream but in upper levels the flow movement toward downstream, showing that a longitudinal vortex is formed.
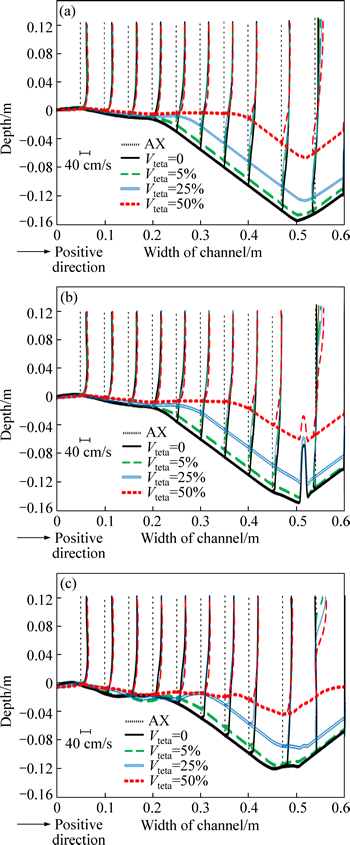
Fig. 6 Longitudinal velocity at cross section of 43.75°(a), 44.5° (b) and 46.25° (c)
3.3 Vertical velocity (Wz)
By spur submergence and in all submergence ratios, the maximum of vertical velocity (toward water surface) occurs near the upstream of spur web, within 13% distance of the channel width from outer bank. In Fig. 8, the vertical velocities in upstream and downstream of the spur dike are shown respectively. In all states, near the inner bank (within a distance of 8% of the channel width from inner bank), the vertical velocity is positive (toward water surface) because of the secondary flow and creating two-way flow in bed and water surface, which leads to movement of the flow from the bed to water surface. By increasing submergence ratio at near the bed, the range of vertical velocity near the spur dike decreases and the area of changes of velocity is more limited.

Fig. 7 Longitudinal velocity in part of channel at section of 44.5° (a) and 46.25° (b)
In all cases near the bed, the maximum of vertical velocity occurs at upstream at the end of spur wing. Since this velocity is positive (upward), an upward-moving flow is created and after reaching the downward flow (due to the collision of longitudinal flow to spur dike), it simultaneously cooperates effectively in forming longitudinal vortices. In all states of submergence and within 42%-58% of the channel width from outer bank (25-35 cm of the inner bank), vertical velocity is positive (upward), whereas within 66%-83% of the channel width from the outer bank (40-50 cm of the inner bank), the depth velocity near scour holes is positive (toward water level), and in higher levels is negative, which indicates downward flow. In Fig. 8(a), the velocity at spur field (10% of the channel width from outer bank) in total depth is negative (toward down), which is the main cause of creating vortices and scouring; but in Fig. 8(c) the velocity is very low at that place. In general by increasing submergence ratio, the vertical velocity at downstream of the spur dike is reduced.
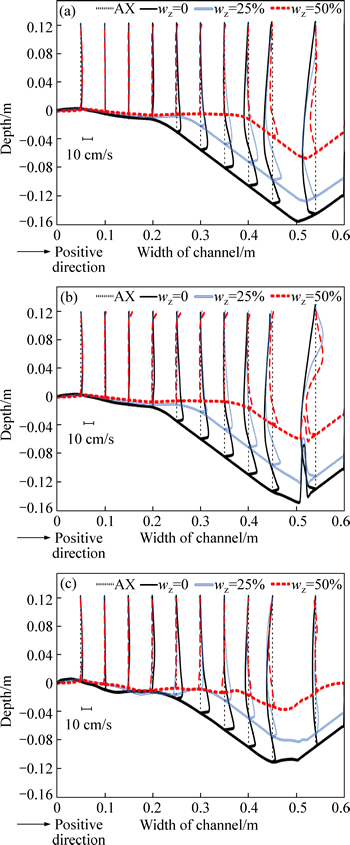
Fig. 8 Vertical velocity at cross section of 43.75° (a), 44.5° (b) and 46.25° (c)
3.4 Comparison of 3D components of flow velocity
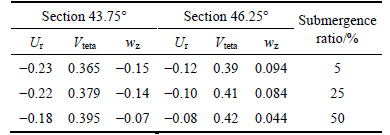
To compare the components of three-dimensional velocity, the maximum transverse, longitudinal and vertical velocities in sections 43.75° (upstream of spur dike) and section 46.25° (downstream of spur dike) as listed in Table 3 are compared together and the differences of them have been identified.
By increasing the submergence ratio of spur dike in two sections, the value of Vteta increases by about 8% and the value of wz about 53% decreases, but the Ur in section 43.75° increases by about 22% and in section 46.25° about 33% has been reduced.
Table 3 Comparison of maximum components of three- dimensional velocity
3.5 Flow pattern of cross section
In Fig. 9, the created vortices in different transverse sections are shown at different non-submerged states. From the beginning of the bend to section 40° (the distance of 2.67L from spur axis toward upstream), the center of vortices caused by secondary flow is near the inner bank. At section 42.5°, there is a new vortex in the center of section and the effect of previous vortex reduced. At section 44.95°, the vortex is only created in the center of section accompanied by downward flows caused by the effect of spur dike. Within distance of 0.6 times spur length from its axis toward upstream (section 46.25° from bend entry), the center of vortex goes toward the outer bank and continues within distance of 7.8L from its axis toward downstream (section 60°); again the vortex is reinforced near the inner bank, that in section 70° is oriented towards the center vortex.
Within distance of 1L to 5.2L from spur axis toward downstream (section 47°-55°), a third vortex is created near the outer bank because of clash of upward and secondary flows. “B” is width of channel and “ds” is scour depth. As seen in Fig. 10, the vortices of mentioned sections are examined at submergence of 5%. The vortices at 5% of submergence are like non-submerged state and follow that process. Only within distance of 1.5L to 7.8L from spur axis toward downstream (section 48°-60° from entry), in addition to the center and inner bank vortex, there is a vortex near the outer bank near the water surface due to the combined effect of upward flow and secondary flow. This vortex in the previous state was at section 48°-55°. At section 44.95°, due to moving of a part of flow from the spur wing to main flow zone, a part of flow goes downward and a part of it goes upward near the outer bank.
Then, in Fig. 11, the submergence ratio of 15% is explored: within distance of 7.8L from its axis toward downstream (section 60°) more flow passes over the spur crest compared to 5% of submergence ratio and joins the central vortex. At section 46.25° in proportion to the submergence ratio of 5%, the upward flow is reinforced. At section 60°, when compared to the previous state, the third vortex which had occurred near the inner bank of section 47°, becomes larger because of more flow passing over spur crest. When this vortex becomes larger, the central vortex is affected and becomes smaller. At section 68°, the third vortex becomes smaller again and the central vortex becomes larger.
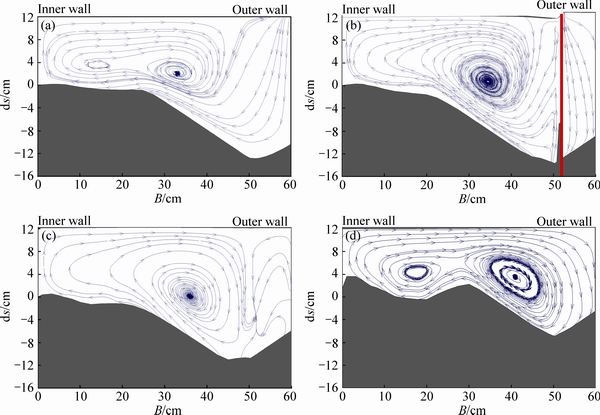
Fig. 9 Flow pattern in non-submerged spur dike at 42.5° (a), 44.95° (b), 46.25° (c) and 60° (d)
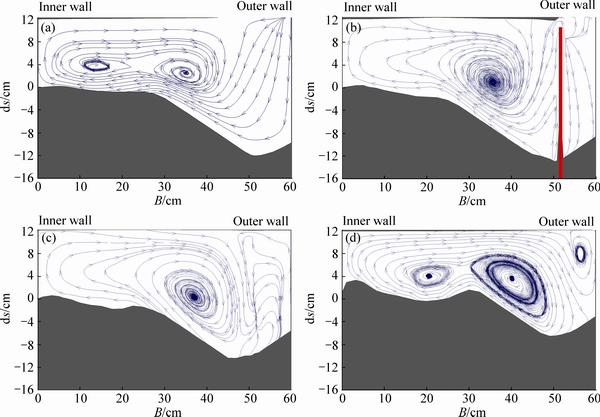
Fig. 10 Flow pattern in 5% of submergence ratio at 42.5° (a), 44.95° (b), 46.25° (c) and 60° (d)

Fig. 11 Flow pattern in 15% of submergence ratio at 42.5° (a), 44.95° (b), 46.25° (c) and 60° (d)
In Figs. 12 and 13, which relates to submergence of 25%, it is seen that within 0.08L from its axis toward upstream (section 44.95°), the secondary vortex is created because of passing more flow over the spur wing and moving the center of vortex toward the outer bank. On the other hand, at 46.25°, the secondary vortex is forming because of the little moving of the vortex toward the inner bank. At section 60°, because the third vortex is reinforced, the main and secondary vortexes fade. At section 68°, like previous, the third vortex formed at section 48°, weakens and the main vortex again dominates. In submergence of 50%, due to the little effect of the spur dike, main vortex is still located near the inner bank and the secondary vortex does not form. At section 44.95° due to the high falling flow over spur dike, the main vortex remains near the inner bank. At section 60°, because of overcoming of the secondary flow on pressure gradient, center of the main vortex, a little deviates toward middle of the channel.
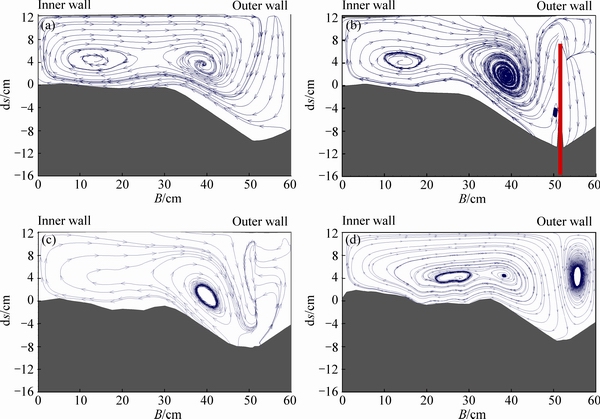
Fig. 12 Flow pattern in 25% of submergence ratio at 42.5° (a), 44.95° (b), 46.25° (c) and 60° (d)
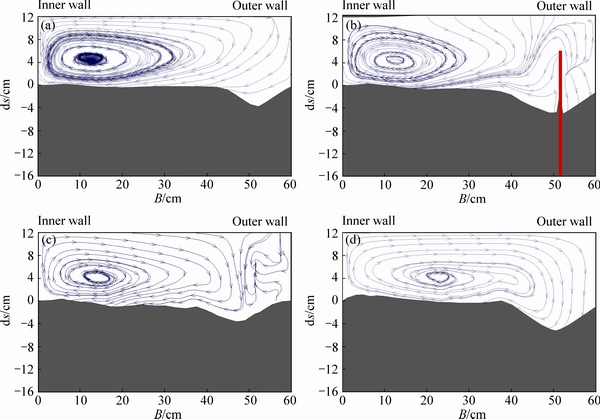
Fig. 13 Flow pattern in 50% of submergence ratio at section 42.5° (a), 44.95° (b), 46.25° (c) and 60° (d)
At section 70°, the secondary flow is created and reinforced. About the dimensions of the created vortex in the section of the spur axis, it was seen that by increasing the submergence ratio, the diameter of the central vortex decreases; therefore, by reducing the power of vortex, it is expected that the scour in the direction of the outer wing of spur dike decreases.
3.6 Flow pattern of longitudinal section
In Fig. 14, the longitudinal section near spur dike within 12% distance of channel width (7 cm from the outer bank), is shown for different submergence ratios. A vortex has been formed upstream of spur web for all submergence ratios due to downward flows after the clash of flow to spur web. After hitting the bed in its route and hitting the longitudinal flows, this flow creates vortex. In submergence of 50%, due to low state of this downward flow, a weak vortex is created. By increasing the submergence ratio, flow’s turbulence in the upper level of spur crest decreases and streamlines continue in straight direction. Within 18% of the channel width (11 cm) from the outer bank, it is seen that by increasing submergence ratio, there is no change in the flow pattern and in all cases streamlines are oriented toward the bed and the area with low pressure at the second half of bend.
3.7 Flow pattern in plan
In Figs. 15 and 16, the flow pattern is shown at the levels of 10% and 50% of flow depth. In the level of 10% of depth, in all states the streamlines approaching the spur dike location are oriented toward inner bank, but by increasing the submergence ratio this great tendency reduces so that in the submergence ratio of 50%, streamlines have also turned toward mid-channel. Also at this depth, formation of vortices caused by the reattachment zone is evident at downstream of spur dike. In 50% of depth, streamlines are less affected by spur dike, and so it has not changed so much and continues along the path. At this level also in the upstream of spur dike the vortex is created, except for the submergence ratio of 50% that has a very weak vortex.
3.8 Scour pattern
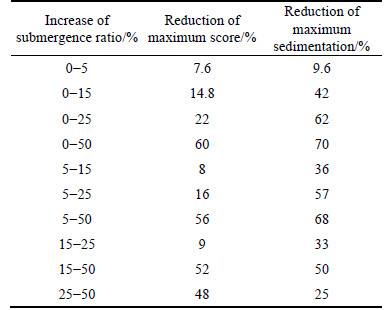
In this work, the main attention is focused on the flow pattern but a summary of the scour pattern has been investigated according to Table 4. By increasing the dike submergence ratio from 0 (non-submerged) to 50%, the maximum amount of scour and sedimentation are reduced. It is worth mentioning that the maximum amount of scour occurs always at the upstream of dike (near the edge of dike wing) and the maximum amount of sedimentation occurs at the channel downstream (near the inner bank).
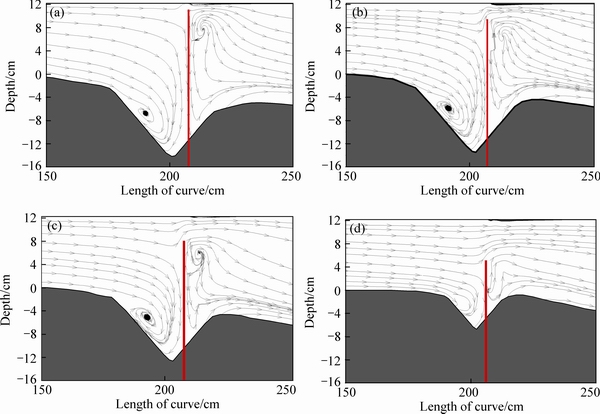
Fig. 14 Flow pattern in longitudinal section in submergence ratio of 5% (a), 15% (b), 25% (c) and 50% (d)
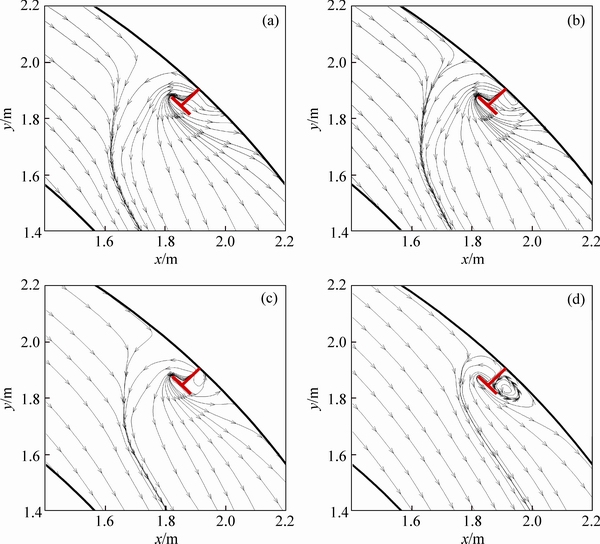
Fig. 15 Flow pattern in plan section equal to 10% of flow depth in submergence ratio of non-submerged (a), 5% (b), 25% (c) and 50% (d)
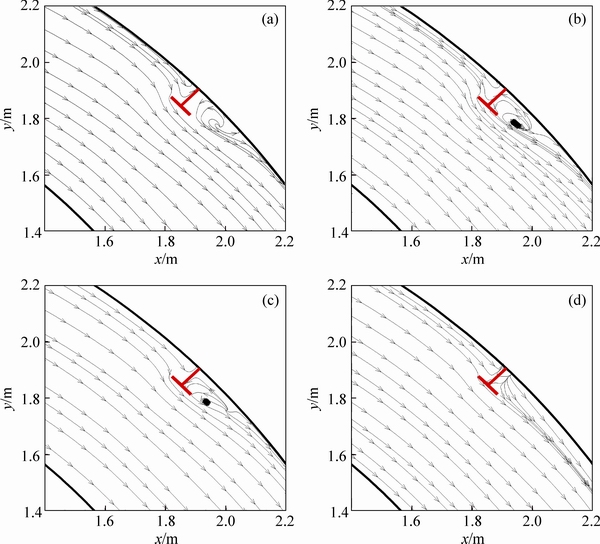
Fig. 16 Flow pattern in plan section equal to 50% of flow depth in submergence ratio of non-submerged (a), 5% (b), 25% (c) and 50% (d)
Table 4 Reduction of the maximum score and sedimentation according to submergence ratio
4 Conclusions
1) By spur dike submergence, the maximum transverse velocity )toward outer bank) occurs in section 47.5° at downstream of spur dike within 10% distance of the channel width from outer bank and 5% distance of flow depth from the bed. However, the maximum transverse velocity toward the inner bank occurs in section 44.9° at upstream of the spur dike and outside its wing within 15% of the channel width from the outer bank and in total, and decreases by increasing the submergence ratio.
2) By increasing the submergence ratio, the scour is reduced but the changes of transverse velocity are not significant, and there is no obvious change in transverse velocities quantity.
3) The transverse velocity increases from inner bank to dike location and decreases when reaching spur dike or outer bank, which is caused by the effect of spur dike on the flow pattern.
4) In submerged case and by increasing submergence ratio from 5% to 50%, the maximum of longitudinal velocity increases by 7.7% and its maximum occurs at the water surface in spur dike axis. On the other hand, the maximum of longitudinal velocity approaches the outer bank by increasing submergence ratio.
5) By increasing the submergence ratio, due to passing of flow over the spur crest, the longitudinal velocity increases at upstream, downstream and at the spur dike axis section, so lower scour occurs at spur upstream and the changes of bed topography decrease.
6) In all submergence ratios, the maximum of vertical velocity (toward water surface) occurs near the upstream of dike web, within 13% distance of the channel width from outer bank.
7) In all cases near the bed, the maximum of vertical velocity occurs at upstream at the end of dike wing. By increasing submergence ratio, the vertical velocity at downstream of the spur dike is reduced.
8) In all submergence ratios a vortex is shaped near the spur web which is due to the effect of downward flows after hitting the flow with spur web. In 50% of submergence ratio due to the weakness of this downward flow, the vortex is very small.
References
[1] Blanckaert K, GRAF W H. Mean flow and turbulence in open- channel bend [J]. Journal of Hydraulic Engineering, 2001, 127(10): 835-847.
[2] Booij R. Measurements and large eddy simulations of the flows in some curved flumes [J]. Journal of Turbulence, 2003, 4(8): 1-17.
[3] Vaghefi M, Akbari M, Fiouz A R. An experimental study of mean and turbulent flow in a 180 degree sharp open channel bend: secondary flow and bed shear stress [J]. KSCE Journal of Civil Engineering, 2016, 20(4): 1582-1593.
[4] Naji abhari M, Ghodsian M, Vaghefi M, Panahpur N. Experimental and numerical simulation of flow in a 90° bend [J]. Flow measurement and Instrumentation, 2010, 21(3): 292-298.
[5] Zhu Zhi-wen, Liu Zhen-qing. CFD prediction of local scour hole around bridge piers [J]. Journal of Central South University, 2012, 19(1): 273-281.
[6] Rajaratnam N, Nwachukwu B A. Flow near groin-like structures [J]. Journal of Hydraulic Engineering, 1983, 109(3): 463- 480.
[7] Rajaratnam N, Nwachukwu B A. Erosion near groin-like structures [J]. Journal of Hydraulic Engineering, 1983, 21(4): 277- 287.
[8] Giri S, Shimizu Y, Surajate B. Laboratory measurement and numerical simulation of flow and turbulence in a meandering-like flume with spurs [J]. Flow Measurement and Instrumentation, 2004, 15(5): 301-309.
[9] Nagata N, Hosoda H, Nakato T, Muramoto Y. Three-dimensional numerical model for flow and bed deformation around river hydraulic structures [J]. Journal of Hydraulic Engineering, 2005, 131(12): 1074-1087.
[10] Fazli M, Ghodsian M, Salehi Neyshabouri S A A. Scour and flow field around a spur dike in a 90 bend [J]. International Journal of Sediment Research, 2008, 23(1): 56-68.
[11] Zhang H, Nakagawa H, Kawaike K, Yasuyuki B. Experiment and simulation of turbulent flow in local scour around a spur dike [J]. International Journal of Sediment Research, 2009, 24(1): 33-45.
[12] Duan J G, He L, Fu X D, Wang Q Q. Mean flow and turbulence around experimental spur dike [J]. Advances in Water Resources, 2009, 32(12): 1717-1725.
[13] Duan J G, He L, Fu X D, Wang Q Q. Turbulent burst around experimental spur dike [J]. International Journal of Sediment Research, 2011, 26(4): 471-476.
[14] Gu Z P, Akahori R, Ikeda S. Study on the transport of suspended sediment in an open channel flow with permeable spur dikes [J]. International Journal of Sediment Research, 2011, 26(1): 96-111.
[15] Chen L P, Jiang J C, Deng G F, Wu H F. Three-dimensional modeling of pollutants transportation in the flow field around a spur dike [J]. International Journal of Sediment Research, 2012, 27(4): 510-520.
[16] Sharma K, Mohapatra P K. Separation zone in flow past a spur dyke on rigid bed meandering channel [J]. Journal of Hydraulic Engineering, 2012, 138 (10): 897-901.
[17] Fang H W, Bai J, He G J, Zhao H M. Calculations of non-submerged groin flow in a shallow open channel by large-eddy simulation [J]. Journal of Engineering Mechanics, 2013, 140(5): 4001-4016.
[18] McCoy A, Constantinescu G, Weber L. Coherent structures in a channel with groin fields: A numerical investigation using LES [C]// Proceedings of the Impacts of Global Climate Change Proceedings of World Water and Environmental Resources Congress. Alaska, USA: ASCE, 2005: 400-416.
[19] Gill M A. Erosion of sand beds around spur dikes [J]. Journal of the Hydraulics Division, 1972, 98(hy9): 91-98.
[20] Acharya A, Duan J G. Three dimensional simulation of flow field around series of spur dikes [C]// Proceedings of World Environmental and Water Resources Congress. California, USA: ASCE, 2011: 2085-2094.
[21] Ghodsian M, Vaghefi M. Experimental study on scour and flow field in a scour hole around a T-shaped spur dike in a 90° bend [J]. International Journal of Sediment Research, 2009, 24(2): 145-158.
[22] Vaghefi M, Ghodsian M, Salehi Neyshabouri S A A. Experimental study on the effect of a T-Shaped spur dike length on scour in a 90 degree channel bend [J]. Arabian Journal for Science and Engineering, 2009, 34(2B): 337-348.
[23] Vaghefi M, Shakerdargah M, Fiouz A R, Akbari M. Numerical investigation of the effect of Froude number on flow pattern around a single T-shaped spur dike in a bend channel [J]. International Journal of Engineering Research, 2014, 3(5): 351-355.
[24] Vaghefi M, Ghodsian M, Adib A. Experimental study on the effect of Froude Number on temporal variation of scour around a T-shaped spur dike in a 90 degree bend [J]. Applied Mechanics and Materials, 2012, 147: 75-79.
[25] Vaghefi M, Shakerdargah M, Akbari M. Numerical investigation of the effect of Froude number on flow pattern around a submerged T-shaped spur dike in a 90° bend [J]. Turkish Journal of Engineering and Environmental Sciences, 2014, 38: 266-277.
[26] Vaghefi M, Mohseni mehr V A, Akbari M. Numerical investigation of wing to web length ratios parameter of T-shaped spur dike in a 90 degree bend on scour pattern [J]. Journal of River Engineering, 2014, 2(3): 45-52.
[27] Vaghefi M, Safarpoor Y, Hashemi S S. Effect of T-shape spur dike submergence ratio on the water surface profile in 90 degree channel bend with SSIIM numerical model [J]. International Journal of Advanced Engineering Applications, 2014, 7(4): 1-6.
[28] Vaghefi M, Shakerdargah M, Akbari M. Numerical study on the effect of ratio among various amounts of submersion on three-dimensional velocity components around T-shaped spur dike located in a 90 degree bend [J]. International Journal of Scientific Engineering and Technology, 2014, 3(5): 675-679.
[29] Vaghefi M, Ahmadi A. Faraji B. The effect of support structure on flow patterns around T-shape spur dike in 90° bend channel [J]. Arabian Journal of Science and Engineering, 2015, 40(5): 1299-1307.
[30] Vaghefi M, Ghodsian M, Salehi Neyshabouri S A A. Experimental study on scour around a T-Shaped spur dike in a channel bend [J]. Journal of Hydraulic Engineering, 2012, 138(5): 471-474.
[31] Olsen N R B. Computational fluid dynamics in hydraulic and sedimentation engineering [R]. Trondheim: Department of Hydraulic and Environmental Engineering, the Norwegian University of Science and Technology, 1999.
[32] Olsen N R B. CFD algorithms for hydraulic engineering [R]. Trondheim: Department of Hydraulic and Environmental Engineering, the Norwegian University of Science and Technology, 2000.
[33] Olsen N R B. CFD modeling for hydraulic structures [R]. Trondheim: Department of Hydraulic and Environmental Engineering, the Norwegian University of Science and Technology, 2001.
[34] Rhie C M, Chow W L. Numerical study of the turbulent flow past an airfoil with trailing edge separation [J]. AIAA Journal, 1983, 21(11): 1525-1532.
[35] HERRMANN S, KLAUS G, KLAUS G. Boundary-layer theory [M]. New York: Springer, 2000.
[36] Olsen N R B, Stokseth S. Three-dimensional numerical modelling of water flow in a river with large bed roughness [J]. Journal of Hydraulic Research, 1995, 33(4): 571-581.
[37] Vaghefi M, Safarpoor Y, Hashemi S S. Effects of relative curvature on the scour pattern in a 90° bend with a T-shaped spur dike using a numerical method [J]. International Journal of River Basin Management, 2015, 13(4): 501-514.
[38] Olsen N R B. A three-dimensional numerical model for simulation of sediment movement in water intakes with multiblock option [R]. Trondheim: Department of Hydraulic and Environmental Engineering, the Norwegian University of Science and Technology, 2011.
[39] Wildhagen J. Applied computational fluid dynamics with sediment transport in a sharply curved meandering channel [D]. Karlsruhe: Institute for Hydromechanics, Karlsruhe Institute of Technology, Germany, 2004.
(Edited by YANG Hua)
Received date: 2015-09-02; Accepted date: 2015-11-01
Corresponding author: Mohammad Vaghefi, Associate Professor; Tel: +98-77-31222401; Fax: +98-77-33340376; E-mail: vaghefi@pgu.ac.ir

