文章编号:1004-0609(2014)06-1434-07
Ni-20Cr-18W高温合金近液相线熔体处理温度场模拟及参数优化
吴志刚,胡 锐,高中堂,张铁邦,李金山
(西北工业大学 凝固技术国家重点实验室,西安 710072)
摘 要:采用电磁场近液相线处理工艺对Ni-Cr-W高温合金熔体进行处理,然后浇铸,可获得整体均匀细小等轴晶铸锭。建立不同质量Ni-20Cr-18W高温合金熔体电磁场近液相线熔体处理温度场有限元模型,分析电流频率和加热功率等感应加热工艺参数及合金质量对熔体温度场分布的影响。给出了一定质量的合金熔体整体均匀保温在液相线附近时所对应的最优工艺参数,得到了熔体质量与对应的最优加热功率间的经验关系式。最优电流频率为200 Hz。研究结果可为优化高温合金近液相线熔体处理工艺参数提供依据。
关键词:Ni-Cr-W高温合金;近液相线铸造;熔体处理;有限元模拟
中图分类号:TG249.9 文献标志码:A
Temperature field simulation and process parameter optimization for near liquidus melt treatment of Ni-20Cr-18W superalloys
WU Zhi-gang, HU Rui, GAO Zhong-tang, ZHANG Tie-bang, LI Jin-shan
(State Key Laboratory of Solidification Processing, Northwestern Polytechnical University, Xi’an 710072, China)
Abstract: When the Ni-Cr-W superalloy melt was held at near liquidus under electromagnetic field and poured into ingot molds, some ingots with uniform fine equiaxed grains can be obtained. The finite element models of temperature field about different masses of Ni-20Cr-18W superalloy melts treated by induction electromagnetic field were established. The effects of the induction melting process parameters such as current frequency, heating power and the mass of the superalloy melt on the distribution of melt temperature field were investigated. The optimal parameters for holding a certain mass of superalloy melt at near liquidus were obtained. An empirical formula of relationship between the mass of superalloys and optimal heating power was established. The optimal current frequency is 200 Hz. The research results provide a useful support for optimizing the induction melting process parameters for near liquidus melt treatment.
Key words: Ni-Cr-W superalloy; near liquidus casting; melt treatment; finite element simulation
高温合金细晶铸件具有晶粒细小、宏观偏析小、拉伸性能和低周疲劳性能良好的优点[1]。晶粒细化的研究已有七八十年的历史,已产生了3种常用的晶粒细化方法:振动法、热控法及化学变质剂法[2]。在这3种方法的基础上发展起来的近液相线细晶铸造技术[3-4]将高温熔体整体均匀地保温在液相线附近后浇铸,能够很好地细化晶粒。XIA等[5]将2618铝合金熔体整体均匀保温在液相线后浇铸,结果得到整体均匀细小的等轴晶组织;而在液相线温度以上浇铸只能得到常规的枝晶组织。王平等[6]的研究表明,对A356铝合金近液相线熔体处理后进行浇铸可以获得整体均匀细小的非枝晶铸件。近液相线细晶铸造技术熔体的浇注温度低,凝固组织为细小等轴晶,充型性好,具有极大的实用意义。
熔体整体近液相线保温是近液相线细晶铸造技术的关键。为获得温度场均匀分布在液相线附近的低温熔体,需要精确控制合金的熔炼及降温过程,主要有电阻炉保温和感应炉保温两种方法。将过热熔体在电阻静置炉中保温,这种方法得到的熔体温度场分布不均匀,不能很好地满足近液相线细晶铸造的要求。在真空感应炉中保温,电磁搅拌作用使熔体温度场分布较均匀[7],熔体温度场能整体均匀分布在液相线附近。但现在并没有确定的工艺参数来对熔体温度控制进行指导。
根据合金真空感应熔炼[8]的特点,拟建立多组不同质量的Ni-20Cr-18W高温合金在电磁场下近液相线熔体处理过程中的电磁-温度场耦合模型[9-11],利用ANSYS软件模拟不同感应熔炼工艺参数下熔体温度场分布,进而研究感应加热工艺参数对熔体温度场分布的影响规律,据此给出一组高温合金近液相线熔体处理的优化参数,为近液相线细晶铸造提供指导。
1 模型建立
1.1 电磁场模型
高温合金真空感应熔炼的原理是利用电磁感应作用在导体内部产生涡流,涡流热效应加热导体,其实质是电能转化为热能的过程。要计算电磁感应对导体产生的热效应,首先要计算感应线圈中通电后在导体内产生的矢量磁位。因此,模拟合金真空感应熔炼过程首先要建立电磁场模型[12]。
电磁场模型由麦克斯韦方程组控制:
 (1)
(1)
式中:H、J、E、D、B、 和t分别表示磁场强度、电流密度、电场强度、电位移、磁通密度、电荷密度和时间,
和t分别表示磁场强度、电流密度、电场强度、电位移、磁通密度、电荷密度和时间,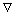 为微分算子:
为微分算子:
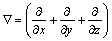 (2)
(2)
为简化电磁场计算,定义两个量来分离电场和磁场变量,分别形成一个独立的磁场和电场的偏微分方程,这样就能简化数值求解过程。定义的两个量分别为矢量磁势A和标量电势 [13]。
[13]。
矢量磁势A定义为
 (3)
(3)
标量电势 定义为
定义为
 (4)
(4)
定义的矢量磁势和标量电势可以自动满足法拉第电磁感应定律和高斯磁通定律,然后将这两个量应用于安培环路定律和高斯电通定律中,分别得到如下磁场偏微分方程和电场偏微分方程[13]:
 (5)
(5)
 (6)
(6)
式中: 和
和 分别表示介质的磁导率和介电常数;
分别表示介质的磁导率和介电常数; 为拉普拉斯算子:
为拉普拉斯算子:
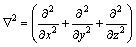 (7)
(7)
采用有限元法对磁场偏微分方程和电场偏微分方程进行数值求解,解得磁势和电势的分布值,通过后处理就能得到电磁场的各种物理量,进而求得电磁感应在导体内产生的热效应。
1.2 温度场模型
合金在真空感应熔炼过程中温度场计算要求解对流边界条件下的热传导方程:
 (8)
(8)
式中:T、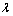 、
、 和cp分别表示合金的温度、热导率、密度和定压比热容;q表示合金的生热率[9]。感应加热过程中,合金的生热率由感应出的涡流产生,合金中任意点处的生热率表示如下:
和cp分别表示合金的温度、热导率、密度和定压比热容;q表示合金的生热率[9]。感应加热过程中,合金的生热率由感应出的涡流产生,合金中任意点处的生热率表示如下:
 (9)
(9)
式中: 和f分别为合金的电导率和加热过程的电流频率[9],而A表示电磁场模型中求解得到的任意点处的矢量磁势。
和f分别为合金的电导率和加热过程的电流频率[9],而A表示电磁场模型中求解得到的任意点处的矢量磁势。
温度场求解的边界条件:设置合金熔体初始温度为T0,熔体与真空接触的边界为辐射边界,实际物体热辐射的计算可以采用斯蒂芬-玻尔兹曼定律[13]的修正形式:
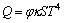 (10)
(10)
式中:Q为热量;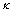 为黑体热辐射常数;S表示热辐射表面积;
为黑体热辐射常数;S表示热辐射表面积; 为实际物体的热辐射率,或称为黑度,其值一般在0~1之间;T为温度。熔体在加热过程中始终不断地向周围空间中发射电磁波,散失热辐射能量。
为实际物体的热辐射率,或称为黑度,其值一般在0~1之间;T为温度。熔体在加热过程中始终不断地向周围空间中发射电磁波,散失热辐射能量。
1.3 有限元模型
对镍基高温合金真空感应熔炼过程进行研究。建立熔炼过程的实体模型如图1(a)所示,图中区域a表示熔体,区域b表示坩埚,区域c表示线圈。感应熔炼过程中交变电流存在集肤效应,电流透入深度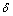 可由下式计算[14]:
可由下式计算[14]:
 (11)
(11)
式中: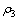 、
、 和f分别表示合金的电阻率、合金的相对磁导率和电流频率。在对实体模型进行有限元网格划分时,合金熔体表面网格单元尺寸设置为
和f分别表示合金的电阻率、合金的相对磁导率和电流频率。在对实体模型进行有限元网格划分时,合金熔体表面网格单元尺寸设置为 ,熔体中心部分网格单元尺寸设置为
,熔体中心部分网格单元尺寸设置为 。
。

图1 高温合金感应熔炼的有限元模型
Fig. 1 Finite element models of superalloy induction melting
由于工程上的需要,根据坩埚型号结合实际情况模拟了质量为10、20、30、40、50和60 kg的Ni-20Cr-18W高温合金感应熔炼过程的温度场,研究感应加热工艺参数和合金质量对温度场分布的影响。不同质量合金的体积不同,熔炼所用坩埚尺寸不同,各组质量的合金对应的熔炼坩埚及建立的有限元模型尺寸如表1所列。
表1 不同质量合金的模型尺寸
Table 1 Sizes of finite element model of different masses of superalloy

2 结果与讨论
求解高温合金真空感应熔炼有限元模型,模拟真空感应炉内熔体的宏观温度场。模拟过程中所用高温合金材料性能参数如表2所列。影响熔体温度场分布的主要工艺参数有真空感应炉的电流频率f,加热功率P以及合金熔体的质量。加热功率不能作为直接的载荷施加在有限元模型上,必须转化成电流密度载荷参与运算,真空感应熔炼炉上可控参数是加热功率P,感应熔炼过程中电源电压为U,感应线圈的截面积为A,则施加到感应线圈上的电流密度JS为
 (12)
(12)
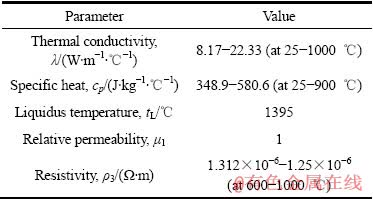
表2 Ni-20Cr-18W高温合金参数
Table 2 Parameters of Ni-20Cr-18W superalloy
2.1 电流频率对熔体温度场的影响
保持合金熔体的质量为60 kg、感应加热的电流 密度为48 MA/m2不变,熔体的温度场分布随电流频率的变化如图2所示。Ni-20Cr-18W高温合金的液相线温度为tL=1395 ℃。
由图2可知,当电流频率为50 Hz时,熔体无法保温在液相线附近;随着时间的延长,熔体温度降至固相线以下,已经凝固。当电流频率由100增大至200 Hz时,熔体内最高温度随电流频率的增大而升高,熔体内最大温差也相应增大,熔体内温度场分布越来越不均匀,如图3所示。
由图2(b)~(d)可以看出,加热电流密度为48 MA/m2时,电流频率在100~200 Hz范围内,熔体温度均高于液相线温度,且电流频率越大,熔体温度越高。由以上结果可知,在电流密度不变的情况下,电流频率越大,感应炉中熔体的涡流热效应越大,这表明要取得相同的热效应,电流频率越小,则需要的电流密度越大。如图2(a)所示,当电流频率为50 Hz时,电流密度高达48 MA/m2仍不能使熔体保温在液相线附近;在电流频率小、电流密度过大的情况下,熔体内温度场分布极不均匀。为使熔体温度均匀分布在液相线附近,需要选取较高的电流频率,同时降低电流密度。

图2 电流频率对合金熔体温度场分布的影响
Fig. 2 Effect of current frequency on temperature field of alloy melt

图3 合金熔体温度与电流频率的关系
Fig. 3 Relationship between alloy melt temperature and current frequency
2.2 电流密度对熔体温度场的影响
选取电流频率为200 Hz,60 kg合金熔体的温度场分布随电流密度的变化如图4和5所示。由图5可知,电流密度从8 MA/m2增大到24 MA/m2的过程中,熔体整体温度逐渐升高;而当电流密度太高或太低时,熔体内温度差都较大,熔体温度场分布不均匀;当电流密度适中时,熔体内温差小,温度场分布均匀。由图4可知,当电流密度为8 MA/m2时,涡流热效应不足以抵消熔体散失的热量,熔体温度降低,直接在感应熔炼炉内凝固。当电流密度为24 MA/m2时,熔体温度显著升高,熔体内最高温度达到1889 ℃,熔体内最大温差为66 ℃,即24 MA/m2过高的电流密度,导致熔体温度过高,远远超出液相线,且熔体温度场分布也不均匀。降低电流密度至16 MA/m2,熔体温度场分布得到一定程度的均匀化,但熔体最高温度高出液相线86 ℃。继续降低电流密度至14.72 MA/m2,熔体温度场均匀分布于液相线附近,低温区最低温度为1378 ℃,在液相线以下17 ℃,低温区熔体内发生形核长大,但在交变电磁场的搅拌作用和强制对流作用下,长大的晶粒会不断破碎或移动到熔体高温区熔断,高温区最高温度为1408 ℃,高于液相线13 ℃,近液相线熔体处理过程中,形核长大和破碎重熔保持动态平衡,导致熔体内弥散了大量的结晶核心[15]。高温合金近液相线熔体保温处理之后浇注,自生形核剂促使熔体内爆发式形核,晶粒细小、均匀,呈球状[16-17],因此,熔体充型过程的流动性也得到了很好的保证。

图4 电流密度对合金熔体温度场分布的影响
Fig. 4 Effect of current density on temperature field distribution of alloy melt

图5 合金熔体温度与电流密度的关系
Fig. 5 Relationship between alloy melt temperature and current density
2.3 不同质量熔体保温在液相线附近合金的温度场分布
在感应加热过程中,电流频率保持在200 Hz,不同质量的合金熔体保温在液相线附近的温度场分布如图6所示,此时不同质量的熔体保温在液相线附近对应的电流密度及加热功率如表3所列。由图6和表3可知:10 kg熔体在电流频率为200 Hz、电流密度为19.8 MA/m2的工艺条件下,能得到近液相线熔体处理的效果,熔体温度保持在液相线(tL=1395 ℃)附近 20 ℃以内;20 kg熔体对应的最优电流密度为17.6 MA/m2,熔体内低温区最低温度为1387 ℃,高温区最高温度为1406 ℃,均保持在液相线附近15 ℃以内。随着熔体质量增加,保持电流频率不变,进行近液相线熔体处理所需要的电流密度降低,如表3所列。合金熔体质量与最优加热功率之间的关系如图7所示。根据式(12)可以由电流密度计算得到真空感应炉的加热功率。合金熔体质量与最优加热功率之间的关系如图7所示。
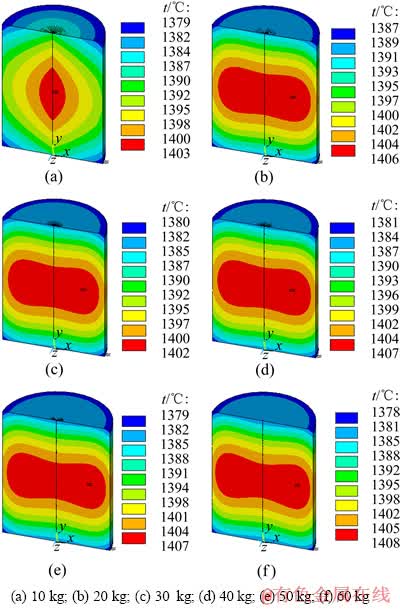
图6 保温在液相线附近不同质量合金熔体的温度场分布
Fig. 6 Temperature field distribution of different masses of alloy melt holding at near liquidus
图7中曲线的经验关系式为
 (13)
(13)
式中:P为加热功率,kW;m为熔体质量,kg。
式(13)可以对高温合金近液相线熔体处理过程中工艺参数的选取提供一定的参考。
表3 不同质量熔体保温在液相线附近时对应的电流密度和加热功率
Table 3 Current density and heating power corresponding to different masses of melt holding at near liquidus


图7 保温在液相线时不同质量熔体的加热功率
Fig. 7 Heating power for different masses of melt holding at near liquidus
2.4 近液相线铸造高温合金铸锭的微观组织
根据模拟结果,60 kg的高温合金近液相线熔体处理工艺参数为电流频率200 Hz、加热功率9.2 kW。
将60 kg的Ni-20Cr-18W高温合金熔体在液相线附近保温后进行浇注,熔体浇注温度为1395 ℃,铸型温度为1150 ℃,得到的铸锭如图8(a)所示:圆柱棒直径105 mm、高度330 mm;冒口部分直径150 mm、高度165 mm。沿图8(a)中的横截面A和B切取10 mm厚的铸锭块,图8(b)表示切取的试样的横截面。
沿图8(b)所示的铸锭横截面的径向切取4个10 mm×10 mm×10 mm的正方体铸锭块制作金相试样,观察铸锭横截面上不同部位的微观组织,结果如图9所示。
图9中(a)、(b)、(c)和(d)分别对应于图8(b)中铸锭横截面上1、2、3和4处的金相显微组织。分析图9可知,60 kg的高温合金块料经真空感应熔炼、近液相线熔体处理后浇注得到的铸锭晶粒均匀、细小,并且在整个横截面上,晶粒都是等轴晶,无传统铸锭的三晶区,铸锭组织基本不存在微观缩松,晶界间隙小,晶粒致密度高。近相线保温处理使熔体中存在大量的近程有序排列的准固态原子集团,这些原子集团在一定过冷度下,迅速长大变成稳定的结晶核心。近液相线凝固时温度场分布比较均匀,利于大量晶核的形成,形核率增大,晶粒来不及长大,所以,形成细小的等轴晶组织。由此可见,在适当的交变电磁场作用下,合金熔体近液相线保温后进行浇注可以得到整体等轴细晶铸锭。

图8 60 kg高温合金铸锭实物图及其截面图
Fig. 8 Physical map(a) and cross section view(b) of 60 kg superalloy ingot

图9 铸锭横截面不同部位处的微观组织
Fig. 9 Microstructures of ingot cross section at different parts
3 结论
1) Ni-20Cr-18W高温合金在电磁场作用下近液相线熔体处理后进行浇注可以得到均匀细小的等轴晶铸锭,这种细晶铸锭无传统铸锭的三晶区,性能优异。
2) 综合考虑电流频率和电流密度对熔体温度场的影响,为得到温度场均匀分布于液相线附近的高温合金熔体,选取200 Hz的电流频率可以有效降低电流密度,提高熔体保温于液相线附近温度场的均匀性。
3) 不同质量的合金在真空感应熔炼过程中,要在液相线附近保温需要适当的加热功率,熔体质量与加热功率之间存在指数经验关系式。
REFERENCES
[1] WANNASIIN J, CANYOOK R, WISUTMETHANGOON S, FLEMINGS M C. Grain refinement behavior of an aluminum alloy by inoculation and dynamic nucleation[J]. Acta Materialia, 2013, 61(10): 3897-3903.
[2] ROBERT T, NOGUEZ M E, SALAS G, MONTEJANO S. Influence of grain refinement on some mechanical properties of non ferrous cast alloys[J]. Acta Metallurgica et Materialia, 1992, 40(4): 771-777.
[3] ZHANG X L, LI T J, TENG H T, XIE S S, JIN J Z. Semisolid processing AZ91 magnesium alloy by electromagnetic stirring after near-liquidus isothermal heat treatment[J]. Materials Science and Engineering A, 2008, 475(1): 194-201.
[4] CZERWINSKI F. Near-liquidus molding of Mg-Al and Mg-Al-Zn alloys[J]. Acta Materialia, 2005, 53(7): 1973-1984.
[5] XIA K, TAUSING G. Liquidus casting of a wrought aluminum alloy 2618 for thixoforming[J]. Materials Science and Engineering A, 1998, 246(1): 1-10.
[6] 王 平, 崔建中. 近液相线法铸造非枝晶A356合金组织与成形性能[J]. 金属学报, 2002, 38(9): 952-955.
WANG Ping, CUI Jian-zhong. Nondendritic microstructure of A356 alloy obtained by the nearby liquidus casting and thixoformed properties[J]. Acta Metallurgica Sinica, 2002, 38(9): 952-955.
[7] 王 晶, 李培杰, 何良菊, 弥光宝, 钟约先. 电磁搅拌对A356合金熔体结构及其凝固行为的影响[J]. 中国有色金属学报, 2009, 19(12): 2090-2098.
WANG Jing, LI Pei-jie, HE Liang-ju, MI Guang-bao, ZHONG Yue-xian. Influence of electromagnetic stirring on structure of A356 melt and its solidification behavior[J]. The Chinese Journal of Nonferrous Metals, 2009, 19(12): 2090-2098.
[8] JIN Wen-zhong, LI Ting-ju, YIN Guo-mao. Research on vacuum-electromagnetic casting of IN100 superalloy ingots[J]. Science and Technology of Advanced Materials, 2007, 8(1): 1-4.
[9] WANG K F, CHANDRASEKAR S, YANG H T Y. Finite- element simulation of induction heat treatment[J]. Journal of Materials Engineering and Performance, 1992, 1(1): 97-112.
[10] KEE H C. Coupled electro-magneto-thermal model for induction heating process of a moving billet[J]. International Journal of Thermal Sciences, 2012, 60: 195-204.
[11] LI Jin-shan, HAO Qi-tang, LI Shuang-ming, KOU Hong-chao, LI Jian-guo, FU Heng-zhi. Research on the non-linear temperature field of molten metal shaped by an electromagnetic field in DS processing[J]. Journal of Materials Processing Technology, 2003, 137(1/3): 145-150.
[12] DONEA J, GIULIANL S, PHILIPPE A. Finite elements in the solution of electromagnetic induction problems[J]. International Journal for Numerical Methods in Engineering, 1974, 8(2): 359-367.
[13] 唐兴伦. ANSYS工程应用教程—热与电磁学篇[M]. 北京: 中国铁道出版社, 2002: 143.
TANG Xing-lun. ANSYS application tutorial—Electromagnetism and thermal papers[M]. Beijing: China Railway Publishing House, 2002: 143.
[14] 姜士林, 赵长汉. 感应加热原理与应用[M]. 天津: 天津科技翻译出版公司, 1993: 10-26.
JIANG Shi-lin, ZHAO Chang-han. Principle and application of induction heating[M]. Tianjin: Tianjin Science and Technology Translation and Publishing Company, 1993: 10-26.
[15] 王连登, 朱定一, 陈永禄, 魏喆良, 李秋菊, 黄利光, 宋 伟, 吴海彬. 熔体温度处理及变质对Al-20%Si合金凝固组织的影响[J]. 中国有色金属学报, 2011, 21(9): 2075-2083.
WANG Lian-deng, ZHU Ding-yi, CHEN Yong-lu, WEI Zhe-liang, LI Qiu-ju, HUANG Li-guang, SONG Wei, WU Hai-bin. Effect of melt thermal treatment and modification on solidification microstructure of Al-20%Si alloy[J]. The Chinese Journal of Nonferrous Metals, 2011, 21(9): 2075-2083.
[16] LI M J, TAMURA T, MIWA K. Controlling microstructures of AZ31 magnesium alloys by an electromagnetic vibration technique during solidification: From experimental observation to theoretical understanding[J]. Acta Materialia, 2007, 55(14): 4635-4643.
[17] LI H T, WANG Y, FAN Z. Mechanisms of enhanced heterogeneous nucleation during solidification in binary Al-Mg alloys[J]. Acta Materialia, 2012, 60(4): 1528-1537.
(编辑 陈卫萍)
基金项目:“高档数控机床与基础制造装备”科技重大专项(2009ZX04006-042);国家重点基础研究发展计划资助项目(2011CB610404)
收稿日期:2013-11-11;修订日期:2014-04-20
通信作者:胡 锐,教授,博士;电话:029-88491764;E-mail: rhu@nwpu.edu.cn