DOI: 10.11817/j.issn.1672-7207.2015.05.045

中央喷射型喷嘴颗粒分布准则关系式

艾元方¹，孙彦文¹，陈红荣¹，刘安明²

(1. 中南大学 能源科学与工程学院，湖南 长沙，410083；

2. 金隆铜业有限公司，安徽 铜陵，244021)

摘要：建立闪速炉中央喷射型精矿喷嘴实验模型，用接粒称重冷模实验方法研究喷嘴控制下的颗粒分布量纲一的准则关系式。研究结果表明：反应塔内颗粒分布受控于绕流雷诺数Re_d和修正弗劳德数Fr′综合作用，大Re_d或小Fr′使颗粒集中分布于喷嘴正下方区域；Re_d对颗粒分布的影响比Fr′的影响大；Re_d和Fr′可以将实验范围内表征各工况颗粒分布均匀性的颗粒比面密度均方差σ和塔中心区域颗粒质量分数x₁二元拟合为非线性指数函数，实验关联式分别为σ=0.001 2exp(2.916Re_d^{0.167 1}/Fr′^{0.099 3})，x₁=11.81exp(-39.15Re_d^{-0.400 9}/Fr′^{-0.242 5})，σ与x₁近似正相关；σ相同的条件是投料量增大倍数n_s和分布风流量增大倍数n_dis关系式满足n_dis=n_s^{1.341 4}。

关键词：中央喷射型精矿喷嘴；颗粒分布均匀性；准则关系式；绕流雷诺数；修正弗劳德数

中图分类号：TF811              文献标志码：A         文章编号：1672-7207(2015)05-1909-06

Criterion relation of particles distribution for CJD nozzle

AI Yuanfang¹, SUN Yanwen¹, CHEN Hongrong¹, LIU Anming²

(1. School of Energy Science and Engineering, Central South University, Changsha 410083, China;

2. Jinlong Copper Co. Ltd., Tongling 244021, China)

Abstract: An experimental model of flash furnace with CJD nozzle was built, the criterion relation of particles distribution was studied, employing cold experimental methods such as receiving particles from air flow and weighting particles. Results show that particles distribution in the reaction tower is controlled by the combined action of streaming Reynolds Number Re_d and modified Froude Number Fr′, the big Re_d or the small Fr′ makes the particles concentrated on the central zone under the nozzle. The effect of Re_d on the particle distribution uniformity is larger than that of Fr′; Re_d and Fr′ are fitted as the nonlinear exponential function with two uniformity indexes of particles distribution, i.e. the mean square error of surface density ratio σ and the central mass fraction x₁ within the scope of experimental data, and the experimental functions are σ=0.001 2exp(2.916Re_d^{0.167 1}/Fr′^{0.099 3}) and x₁=11.81exp(-39.15Re_d^{-0.400 9}/Fr′^{-0.242 5}). σ is positively related to x₁, the condition that σ is the same is that the amplification factor of concentrate loading n_s and distribution air n_dis satifies n_dis=n_s^{1.341 4}.

Key words: CJD burner; particles distribution uniformity; criterion relation; streaming Reynolds Number; modified Froude Number

中央喷射型精矿喷嘴因生产潜能大、节能环保等优势而在铜镍铅锌冶炼企业得到广泛应用，但目前人们对喷嘴性能调节规律理论研究不多，喷嘴操作水平不高，当今大投料量条件下闪速炼铜炉况优化工作效率不高。喷嘴控制的塔内颗粒分布具有影响因素多、反应慢、呈非线性而且大滞后等特点^[1]，这说明了闪速炉热工特性的复杂性和研究难度。在闪速炉热工特性研究方法中，数值模拟方法占多数，冷模实验方法较少。Solnordal等^[2]对奥林匹克坝闪速炉塔内气粒两相流动、传热和冶炼进行仿真研究，发现仿真结果对粒度变化非常敏感，塔内气流和颗粒均分布于塔中心区域。Davidson^[3]采用数值模拟方法证实塔内颗粒流动受限于气流流动。Koh等^[4]通过仿真研究了锌闪速炉中颗粒粒径对颗粒流动的影响。Varnas等^[5]模拟研究镍闪速炉塔内气粒两相流动、传热和冶炼反应规律。Sasaki^[6]仿真发现颗粒呈弥散状均匀分散于塔内。Li等^[7]借助CFX软件模拟贵溪闪速炉得到塔内流场、温度场、浓度场、燃烧释热场以及颗粒轨迹与温度，发现颗粒轨迹呈伞状均匀分布于塔内。Higgins等^[8]建立稳态轴对称模型，模拟发现颗粒粒度、风幕风入炉角度等影响塔内颗粒聚集和分布，颗粒聚集程度主要受颗粒气流质量比、粒度和反应塔入口处湍流强度等影响。Debrincat等^[9]研究了颗粒参数对塔内颗粒聚集的影响。Nagai等^[10]研究发现粒子掺混到工艺风气流更有助于冶炼反应完全。Chen等^[11-13]运用Fluent软件对金隆闪速炉进行单参数优化模拟研究，发现精矿颗粒呈伞状均匀分布于反应塔内，工艺风、分布风和中央氧影响塔内颗粒分布均匀性，分布风流量加大或旋流使颗粒分散更均匀。Ahokainen等^[14]研究了奥托昆普闪速塔内气粒两相流变化规律。Zhou等^[15]基于灰色理论研究了喷嘴外下料均匀性随其主要影响因素变化的规律。Koh等^[16]建立了镍闪速炉冷模装置，发现通过分散锥后的颗粒集中于塔中心区域流动。这些研究获得的颗粒分布规律存在差异，很少有文献解释分析这些差异，即使是单参数优化研究，也很少见到颗粒分布量纲为1的准则关系式报道。这些研究侧重点不同，且受当时研究条件限制，颗粒分布规律缺乏普遍适用价值。另外，对具有普遍适用和推广价值、包括颗粒分布影响因素在内的准则数及其准则关系式或半准则关系式的研究较少。考虑到喷嘴出口附近区域近似常温，且受反应塔中下部及沉淀池高温影响小，作者建立中央喷射式精矿喷嘴冷态模型装置，采用接粒称重冷模实验方法研究喷嘴出口附近区域颗粒分布变化规律，二元拟合归纳出颗粒分布均匀性特征指标随主要准则数变化的实验关联式，论证塔内颗粒分布调控规律，以便为增大投料量条件下现场喷嘴主控参数优化提供参考。

1  颗粒分布准则关系式

1.1  颗粒分布均匀性指标

颗粒比面密度均方差和喷嘴正下方中心区域颗粒质量分数为反应塔内颗粒分布均匀性指标。

颗粒比面密度均方差定义式为

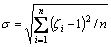              (1)

式中：ζ_i =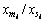，为第i接粒区比面密度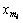；= m_i/Σm_i×100%，为第i接粒区颗粒质量分数(%)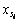；=S_i/ΣS_i×100%，第i接粒区面积分数；m_i和S_i分别为第i接粒区颗粒质量和面积；i=1为喷嘴正下方中心R≤90 mm接粒单元格；n为接粒网格总数量。式(1)中，σ=0表示颗粒质量均匀分布，σ越大，则颗粒质量分布越不均匀。

喷嘴正下方中心区域(R≤90 mm)颗粒质量分数计算式为

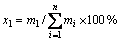           (2)

x₁反映颗粒分布均匀性状况，x₁越大，则颗粒质量分布越不均匀。

1.2  颗粒分布准则数

不同于气固流化床和除尘器气粒两相流规律^[17]，闪速炉反应塔内气粒两相流流动方向相同，且存在多股气流相互交叉和混合作用。从理论上讲，反应塔内颗粒受力有重力、浮力、气动阻力、压强梯度力、附加质量力、Basset力、Saffman力、Magnus力等。对喷嘴附近颗粒，由牛顿第二定律可知

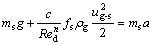          (3)

式中：Re_d为绕流雷诺数，Re_d = u_g-s·d/ν_g，反映粒子周围气流状态及其相互作用；u_g-s为气粒两相相对速度，即气体绕流速度，u_g-s = u_g-u_s；u_g为按工艺风出口面积计算的工艺风气流速度；d为塔内平均粒度；ν_g为塔内气相运动黏度，ν_g = μ_g / ρ_g；ρ_g为气相密度；f_s为迎风面粒子横截面积，f_s = πd²/4；m_s为颗粒质量，m_s = ρ_sπd³/6；a为颗粒加速度；g为重力加速度；c和n为实验常数。

将式(3)左边两项相比并整理得

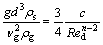               (4)

考虑到阿基米德数Ar定义，将式(4)整理为

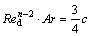                (5)

在c，n和Ar不变时，气粒两相中粒子行为取决于Re_d。反应塔内颗粒流主要受工艺风气流、分布风气流、中央氧气流和颗粒流等综合作用。分布风和颗粒流综合作用采用修正弗劳德数表示。修正弗劳德数Fr′定义为分布风动量和粒子流动量之比，即

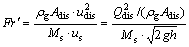        (6)

式中：u_dis为分布风离开分布风孔时的速度；A_dis为分布风孔总面积；Q_dis为分布风总流量；h为料仓底部离分布风孔中心平面的高度；M_s为颗粒质量流量。

1.3  颗粒分布准则关系式

考虑式(3)实际存在的其他作用力，能推导出更多更全面的准则数。由于冷模实验工作量和Matlab软件拟合功能限制，在影响颗粒分布均匀性的众多准则数中，只考虑绕流雷诺数和修正弗劳德数。实验研究目的是变化绕流雷诺数(变化工艺风流量)和修正弗劳德数(变化分布风流量)，拟合整理归纳σ=f(Re_d, Fr′)和x₁=g(Re_d, Fr′)。

2  实验装置

中央喷射型喷嘴及反应塔模型如图1所示。喷嘴从外向内依次为工艺风通道、下料通道、分布风通道和中氧央管。工艺风为闪速冶炼反应提供主要氧化剂，入口带有调风锥，工艺风入口面积可调节；料仓颗粒通过减速电机带动刮板给料机连续下料进入喷嘴下料通道，4个给料机周向均匀布置。为确保实验精度，4个料仓由同一开关控制，同时开启和关闭；分布风从分散锥侧壁风孔射流喷出，压力高、流量小，使颗粒径向分散；中央氧为纯氧，流量较小，以补充冶炼反应不足的氧气。颗粒在分散锥曲面和分布风综合作用下掺入工艺风气流，实现气粒均匀混合。工艺风流量用LU125涡街流量计测量，精度为±1%；分布风流量用LU40涡街流量计测量，精度为±1%；中央氧流量用LU25涡街流量计测量，精度为±1%。

闪速炉模型与原型几何比1:5，模型塔内径为1 106 mm，高为778 mm(本文主要研究喷嘴附近区域颗粒分散和分布特性，模型反应塔高度只取反应塔整个高度的1/3)，料仓出料口高出塔顶3.68 m。工艺风出口内径为100.0 mm，外径为146.4 mm。下料通道内径为36.0 mm，外径为80.0 mm。分布风孔沿圆周均匀分布，直径为1.0 mm，数量为150个。分散锥底圆直径为72.0 mm，中央氧管内径为16.0 mm。塔顶内壁面比冷却水套底面高40.0 mm，比分散锥底圆面高85.0 mm。

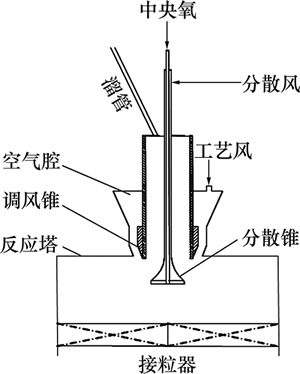
图1  实验装置示意图

Fig. 1  Schematic diagram of experiment device

接粒网格划分如图2所示。接粒器由5个半径分别为90，240，340，440和553 mm的同心圆组成，除中心圆外，其余各圆周向等分成12个扇形区。反应塔出口面与接粒器顶面密封连接，接粒器由网格架和过滤袋组成，实验颗粒不能通过过滤袋，因此，颗粒留在过滤袋中，气体经过滤袋小孔溢出。接粒器设计有过渡段，以避免分离时气流回流对塔内气粒两相流动的影响，提高实验精度，最后称量接粒袋中的颗粒质量并进行分析。接粒质量用A1-31K电子秤称量，精度为±0.2 g。

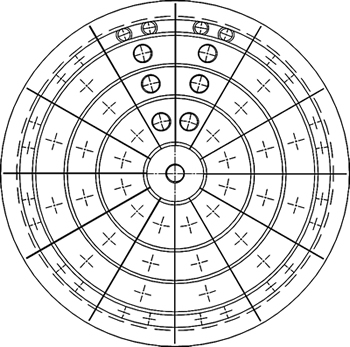
图2  接粒网格划分

Fig. 2  Division of gas-solid separation area

原型喷嘴附近区域温度低，化学反应影响小，可忽略，简化为与模型相近。因此，本文以喷嘴附近区域作为研究对象，研究喷嘴出口附近区域绕流雷诺数和修正弗劳德数对颗粒分散影响规律。

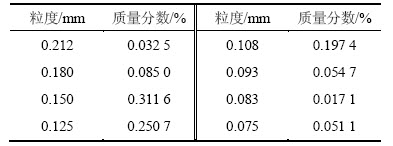
表1  颗粒粒度分布

Table 1  Distribution of particle size

3  结果和讨论

分别变化绕流雷诺数Re_d和修正弗劳德数Fr′，各接粒区颗粒质量称量后可计算出颗粒比面密度均方差σ和塔中心区域颗粒质量分数x₁变化。在等Fr′条件下，σ=f₁(Re_d)离散点集和x₁=g₁(Re_d) 离散点集分别如图3和图4所示。

从图3可以看出：Re_d和Fr′对塔内颗粒分布均匀性有直接影响；σ随Fr′增大而减小，随Re_d增大而增大；当Fr′不变时，Re_d逐渐增大，即工艺风流量逐渐增大，σ逐渐增大，即颗粒分布逐渐不均匀。由于随着Re_d增大，逐渐增大的轴向向下工艺风气流作用限制了颗粒的径向分散，更多的颗粒集中于喷嘴的正下方区域，颗粒分散和分布更加不均匀。当Fr′较小时，σ曲线斜率大，说明此时Fr′对颗粒分布影响较小，而当Fr′较大时，σ曲线斜率小，说明较大的Fr′能明显影响颗粒的分散和分布。由于当Re_d较小时，Fr′的增大在一定程度上能使σ减小，即当分布风相对颗粒流的作用力逐渐增强时，颗粒径向分散作用增大，塔内颗粒分布逐渐趋于均匀，但Fr′越大，颗粒分散所需要增加的动量越大，塔内颗粒分布趋于均匀的程度减小，见图3中左下角区域。

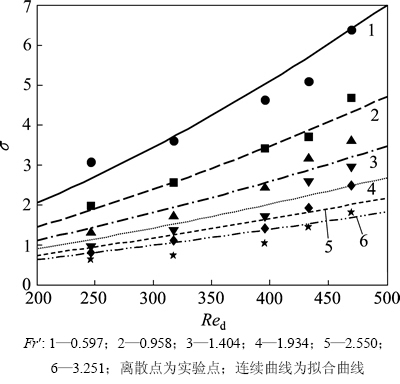
图3  不同Fr′ 时Re_d变化对σ的影响

Fig. 3  Effect of Re_d on σ at different Fr′

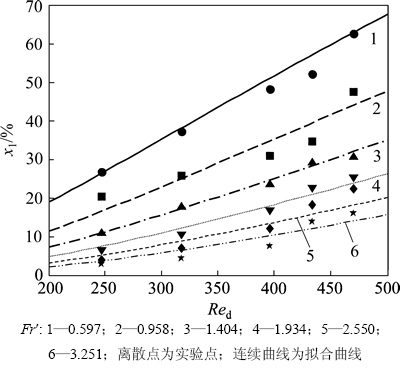
图4  不同Fr′ 时Re_d变化对 x₁的影响

Fig. 4  Effect of Re_d on x₁ at different Fr′

从图4可知：不同Fr′时x₁随Re_d变化的规律与σ随Re_d变化的规律一致；Fr′能使颗粒沿半径方向射流分散，且随其数值的增大，分散作用越强，x₁也越小；Re_d可使颗粒集中于塔中心区域，随着Re_d增大，塔下方中心区颗粒越多，颗粒分布越不均匀。可见：在实验数据范围内，x₁与σ呈正相关趋势。其原因为：当外壁区域颗粒分布没有失真(由于径向分散力较大，颗粒在未到达接粒器平面时已经碰触塔壁而留在外壁区域)时，中心区域颗粒占主要部分，颗粒质量分布不均主要表现在塔中心区域颗粒较多，即x₁较大，因此，σ较大。

Re_d和Fr′对颗粒分散起着重要作用。以Fr′=0.597为例，当Re_d由247增大到318时，增幅为28.75%，而对应的x₁则由26.76%增大到37.34%，增幅为39.54%；当Re_d =247时，Fr′由0.597增大到0.958，增幅为60.47%，而对应的x₁则由增26.76%减小到20.88%，减幅为21.97%。这说明Re_d对颗粒运动和分布的影响比Fr′的影响大。

采用Matlab软件二元非线性拟合模块寻求σ和x₁与Fr′和Re_d之间的关联式。经多次模型最小二乘法回归分析后自定义非线性回归模型如下：

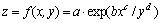          (7)

式中：x和y分别代表Re_d和Fr′；指数c和d为常数，分布代表两者相对权重。整个回归模型以指数函数为主，a和b为常数。模型有效性主要以可决系数r²接近1.000 0的程度来确定。利用Matlab软件进行多次回归分析，计算结果见表2。

表2  回归系数置信区间

Table 2  Confidence interval of regression coefficient

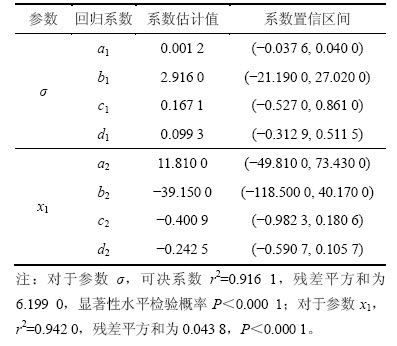
σ，x₁与Re_d和Fr′的实验关联式分别为：

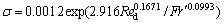 (0.597≤Fr′≤3.251，247≤Re_d≤470)      (8)

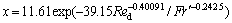 (0.597≤Fr′≤3.251，247≤Re_d≤470)      (9)

由式(8)和式(9)得出的Fr′等值线簇分别如图3和图4中拟合曲线所示。显然，经计算所得可决系数分别为0.916 1和0.942 0，说明此模型在置信区间内是可靠的，拟合曲线和实验点吻合较好。系数c绝对值大于d，说明Re_d对颗粒分布影响大于Fr′的影响。设投料量增大到原来的n_s倍，工艺风流量增大到原来的n_pro倍，分布风流量增大到原来的n_dis倍，则在相同的料仓高度、粒度、分布风孔、工艺风与颗粒配比和工艺风含氧体积分数条件下，要使σ相等，则要求Fr′μRe_d^{1.682 8}，n_pro=n_s，n_dis=n_s^{1.341 4}；要使x₁相等，则要求满足Fr′μRe_d^{1.653 2}，n_pro=n_s，n_dis=n_s^{1.326 6}。因此，在实际闪速炉生产时，并非简单的等比例放大关系，而是随着投料速度的增大，颗粒的运动和分布存在更复杂的指数关系。

4  结论

1) 中央喷射式喷嘴颗粒分布均匀性可调可控。反应塔内颗粒分布受控于绕流雷诺数和修正弗劳德数综合作用。绕流雷诺数使颗粒集中分布于喷嘴正下方区域，修正弗劳德数使颗粒远离喷嘴正下方区域分布。绕流雷诺数Re_d对颗粒分布的影响作用大于修正弗劳德数Fr′的影响。

2) 绕流雷诺数Re_d和修正弗劳德数Fr′可以将实验范围内表征各工况塔内颗粒分布均匀性的指标，即颗粒比面密度均方差σ和塔中心区域颗粒质量分数x₁，二元拟合为非线性指数函数，实验关联式分别为

σ=0.001 2exp(2.916Re_d^{0.167 1}/Fr′^{0.099 3})

x₁=11.81exp(-39.15Re_d^{-0.400 9}/Fr′^{-0.242 5})

可决系数r²分别达到0.916 1和0.942 0。颗粒比面密度均方差σ与塔中心区域颗粒质量分数x₁近似正相关。

3) 优化绕流雷诺数和修正弗劳德数，能实现颗粒分布均匀。在实验范围内，要使颗粒比面密度均方差σ相等，则要求绕流雷诺数Re_d和修正弗劳德数Fr′关系式满足Fr′μRe_d^{1.682 8}，投料量增大倍数n_s和分布风流量增大倍数n_dis关系式满足n_dis=n_s^{1.341 4}；要使塔中心区域颗粒质量分数x₁相等，则要求绕流雷诺数Re_d和修正弗劳德数Fr′关系式满足Fr′μRe_d^{1.653 2}，投料量增大倍数n_s和分布风流量增大倍数n_dis关系式满足n_dis=n_s^{1.326 6}。

参考文献：

[1] MEI Chi, ZHOU Jiemin, PENG Xiaoqi, et al. Simulation and optimization of furnaces and kilns for nonferrous metallurgical engineering[M]. Berlin: Springer, 2010: 1-50.

[2] Solnordal C B, Jorgensen F R A, Koh P T L, et al. CFD modelling of the flow and reactions in the Olympic Dam flash furnace smelter reaction shaft[J]. Applied Mathematical Modelling, 2006, 30(11): 1310-1325.

[3] Davidson M R. Comparison of two-way coupling models for confined turbulent gas–particle jets in flash smelting[J]. Applied Mathematical Modelling, 1998, 22(1/2): 39-55.

[4] Koh P T L, Nguyen T V, Jorgensen F R A. Numerical modelling of combustion in a zinc flash smelter[J]. Applied Mathematical Modelling, 1998, 22(11): 941-948.

[5] Varnas S R, Kemori N, Koh P T L. Evaluation of nickel flash smelting through piloting and simulation[J]. Metallurgical and Materials Transactions B: Process Metallurgy and Materials Processing Science, 1998, 29(6): 1329-1343.

[6] Sasaki Y. Prediction of combustion phenomena in flash smelting furnace for production enhancement using a mathematical model[C]// Sohn Int Symp Advanced Processing of Metals and Materials. San Diego, USA, 2006: 545-559.

[7] LI Xinfeng, PENG Shiheng, HAN Xiangli, et al. Influence of operation parameters on flash smelting furnace based on CFD[J]. Journal of University of Science and Technology Beijing, 2004, 11(2): 115-119.

[8] Higgins D R, Gray N B, Davidson M R. Simulating particle agglomeration in the flash smelting reaction shaft[J]. Minerals Engineering, 2009, 22(14): 1251-1265.

[9] Debrincat D P, Solnordal C B, van Deventer J S J. Influence of particle properties on the size of agglomerated metallurgical powders[J]. Int Journal Miner Process, 2008, 87(1/2): 17-27.

[10] Nagai K, Takebayashi M, Sasai S. Development of the Sumitomo type combustion accelerated concentrate burner[C]// 12th Int Flash Smelting Congress. Shanghai, China, 2008: 146-155.

[11] CHEN Zhuo, WANG Yunxiao. Simulation study of intensified flash smelting process[C]// Dipl Ing Jens Harre GDBM Copper. Hamburg: Papierflieger, 2010: 1313-1323.

[12] 陈卓, 王云霄, 宋修明, 等. 高投料量下炼铜闪速炉内熔炼过程的数值模拟[J]. 中国有色金属学报, 2011, 21(11): 2916-2921.

CHEN Zhuo, WANG Yunxiao, SONG Xiuming, et al. Numerical simulation of smelting process in copper flash smelters at high loading rate[J]. The Chinese Journal of Nonferrous Metals, 2011, 21(11): 2916-2921.

[13] 陈卓, 殷术贵, 周俊, 等. 铜闪速炉分布风旋流喷吹的数值模拟[J]. 过程工程学报, 2012, 12(1): 1-8.

CHEN Zhuo, YIN Shugui, ZHOU Jun, et al. Numerical simulation of copper flash smelting process with rotarily distributed air[J]. Chinese Journal of Process Engineering, 2012, 12(1): 1-8.

[14] Ahokainen T, Jokilaakso A. Numerical simulation of the Outokumpu flash smelting furnace reaction shaft original[J]. Canadian Metallurgical Quarterly, 1998, 37(3/4): 275-283.

[15] ZHOU Ping, YAO Yingjin, AI Yuanfang, et al. Grey correlation analysis of factors influencing maldistribution in feeding device of copper flash smelting[J]. Journal of Central South University, 2012, 19(7): 1938-1945.

[16] Koh P T L, Jorgensen F R A, Elliot B J. Solids falling in flash furnace burner concentrate chutes[J]. Int Journal Miner Process, 2007, 83(3/4): 81-88.

[17] 李之光. 相似与模化: 理论及应用[M]. 北京: 国防工业出版社, 1982: 1-35.

LI Zhiguang. Similarity and modeling: Theory and applications[M]. Beijing: National Defence Industry Press, 1982: 1-35.

(编辑  陈灿华)

收稿日期：2014-05-10；修回日期：2014-07-08

基金项目(Foundation item)：国家高技术研究发展计划(863计划)项目(2010AA065200)；中南大学中央高校基本科研业务费专项资金资助项目(2012zzts087) (Project(2010AA065200) supported by the National High Technology Research and Development Program of China(863 Program); Project(2012zzts087) supported by College Basic Scientific Research Business of Central South University)

通信作者：艾元方，博士，副教授，从事可控燃烧反应机理与技术研究；E-mail: yfai@csu.edu.cn