基于铝电解槽等效电路仿真的气泡对槽电压波动的影响
来源期刊:中国有色金属学报(英文版)2015年第1期
论文作者:王永良 铁 军 涂赣峰 孙树臣 赵仁涛 张志芳
文章页码:335 - 344
关键词:铝电解;等效电路;气泡;槽电压;阳极效应
Key words:aluminum electrolysis; equivalent circuit; gas bubble; cell voltage; anode effect
摘 要:建立一种研究气泡对槽电压波动影响的方法,该方法将整个电解槽等效为一个电阻电路,并利用Matlab/Simulink仿真软件建立等效电路的仿真模型进行动态仿真研究,从而获得不同气泡状态下槽电压和阳极电流的时间序列数据,利用频谱和统计分析方法对这些数据进行分析。结果显示,较高的气泡释放频率对槽电压波动的影响更大,当一组阳极表面气泡覆盖率超过80%时,槽电压可能超出正常的波动范围。仿真结果证实了在实际生产中计算机监测到的阳极效应主要是全槽的阳极效应。
Abstract: A method to investigate the effect of gas bubble on cell voltage oscillations was established. The whole aluminum electrolysis cell was treated as a resistance circuit, and the dynamic simulation of the cell equivalent circuit was modeled with Matlab/Simulink simulation software. The time-series signals of cell voltage and anode current were obtained under different bubble conditions, and analyzed by spectral and statistical analysis methods. The simulation results show that higher bubble release frequency has a significant effect on the cell voltage oscillations. When the bubble coverage of one anode block exceeds 80%, the cell voltage may exceed its normal fluctuation amplitude. The simulation also proves that the anode effect detected by computer in actual production is mainly the whole cell anode effect.
Trans. Nonferrous Met. Soc. China 25(2015) 335-344
Yong-liang WANG1, Jun TIE2, Gan-feng TU1, Shu-chen SUN1, Ren-tao ZHAO2, Zhi-fang ZHANG2
1. School of Materials and Metallurgy, Northeastern University, Shenyang 110819, China;
2. College of Mechanical and Materials Engineering, North China University of Technology, Beijing 100144, China
Received 21 March 2014; accepted 26 June 2014
Abstract: A method to investigate the effect of gas bubble on cell voltage oscillations was established. The whole aluminum electrolysis cell was treated as a resistance circuit, and the dynamic simulation of the cell equivalent circuit was modeled with Matlab/Simulink simulation software. The time-series signals of cell voltage and anode current were obtained under different bubble conditions, and analyzed by spectral and statistical analysis methods. The simulation results show that higher bubble release frequency has a significant effect on the cell voltage oscillations. When the bubble coverage of one anode block exceeds 80%, the cell voltage may exceed its normal fluctuation amplitude. The simulation also proves that the anode effect detected by computer in actual production is mainly the whole cell anode effect.
Key words: aluminum electrolysis; equivalent circuit; gas bubble; cell voltage; anode effect
1 Introduction
Pre-baked anode aluminum electrolysis cell is the main equipment in the production of aluminum. It is actually an electrochemical cell with multi-anode and single cathode. In the cell, alumina dissolves in the melt cryolite between anode and cathode. When anode current density is in normal conditions, the following reaction mainly occurs at the carbon block immersed in the electrolyte:
Al2O3+1.5C(s)=2Al(l)+1.5CO2(g) (1)
In this reaction, CO2 is produced. Because the producing bubbles underneath the anode block cannot be discharged in time, bubbles are partly attached to the underneath surface of the anode, and also some mix with the electrolyte. Due to the poor electrical conductivity of gas, all of these bubbles will increase the resistance of the electrolytic circuit [1,2]. The variation in the cell resistance will cause the change of current distribution and cell voltage fluctuation. The extra cell voltage drop due to gas bubbles may be in the range of 0.15-0.35 V [3], which has a significant loss of energy through Ohmic heating.
Bubble covering the surface of the anode carbon block not only increases the resistance between anode and cathode, but also reduces anode contact area with the electrolyte, which will influence the electrochemical reaction on the anode surface. At the same time, it is the main driver for alumina mixing and bath flow [4]. So, the gas bubbles play an important role in cell operation.
The aluminum reduction cell is a highly corrosive closed system with high temperature. It is difficult to directly observe and determine the gas generation and release processes, so researches on the anode gas are mainly conducted through laboratory study and physical- mathematical model [4-6]. These researches investigated the bubble creation, detachment, transport and its impact on the cell voltage based on small size electrolysis cells or room temperature hydrodynamic models. The gas bubble behavior depends on the anode current density, anode shape and inclination, and electrolysis parameters [7,8]. Lots of research results [1,9] show that the gas coverage fraction on the anode surface is 30%-60%. In addition, the bubbles release periodically from the anode surface, which will disturb the electrolyte and affect liquid aluminum fluctuation. The release frequency of the bubbles is 0.3-3 Hz [10,11]. The relation between cell voltage fluctuation and bubble noise was also investigated [3,12], showing that bubbles are subjected to the frequency and the amplitude of the voltage oscillations. From these studies, we have known about the formation, growth, and motion of gas bubbles to a certain extent.
However, most of these studies are based on a single anode electric field [1,2,4,8]. It is different to the real cell, which contains a multi-anode and a single cathode. When the gas bubbles under the anode bottom surface come to change, the anode current will redistribute. The authors have not found published studies on the numerical model of anode gas bubbles concerning the multi-anode phenomenon in aluminum cell.
The main idea of this work is to simplify the aluminum electrolytic cell as an electrical resistance circuit model, and build the simulation model with Matlab/Simulink simulation software. In this work, it is assumed that the liquid aluminum fluctuation waveform is a sine wave, and bubbles release from the anode surface periodically. Considering the change of alumina concentration and anodic overvoltage, the effect of different bubble release frequencies and coverage fraction on the current distribution and cell voltage is studied by statistical and spectral analysis methods.
2 Description of cell physical model
In the production of aluminum, constant DC current feeds the anode rod from the busbar, flows through the anode carbon block, electrolyte, liquid aluminum, cathode block, and finally outflows from the cathode bars. If the cell can be seen as a resistance circuit, wherein the anode rod, cathode block and cathode bars can be regarded as fixed resistors. Since the liquid aluminum has a very low electrical resistivity, its resistance can be neglected. Furthermore, there are some variable resistors between anode and cathode. Figure 1 shows the equivalent circuit schematic diagram of part aluminum electrolysis cell.
So, the cell voltage (U) can be represented as
U=E re+RanI+RovI+RacdI+R buI+RcaI+RotherI (2)
where Ere is the reaction electromotive force and Rother is the resistance of cathode bar.
The anode is consumed as the current flows through, so its resistance gradually decreases. Moreover, the anode is also an electric conductor. The anode resistance decreases very slowly within a short time. In order to simplify the calculation model, this study assumes that the anode is consumed uniformly. That is to say, the resistance is uniformly reduced in a pole changing period. In this work, it is assumed that the anode consumption period is 28 d according to the actual production process.

Fig. 1 Equivalent circuit schematic diagram of part aluminum electrolysis cell
In normal production the main reaction (1) occurs in the cell. According to the Nernst’s equation, the reaction electromotive force Ere can be given as
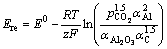 (3)
(3)
where is partial pressure of CO2; αAl,
is partial pressure of CO2; αAl,  and αC are the aluminum, alumina and carbon activity, respectively; R is mole gas constant; F is Faraday’s number; T is reaction temperature in Kelvin; E0 is the standard potential, which is a function of temperature. In the reaction (1), E0 is [13]
and αC are the aluminum, alumina and carbon activity, respectively; R is mole gas constant; F is Faraday’s number; T is reaction temperature in Kelvin; E0 is the standard potential, which is a function of temperature. In the reaction (1), E0 is [13]
E0=-1.8984+5.725×10-4T (4)
z is number of electrons involved in a reaction, here z=12.
Assuming that  =1, αAl =1, αC=1, then,
=1, αAl =1, αC=1, then,
 (5)
(5)
In the bath, the activity of Al2O3 can be expressed as [14]
 (6)
(6)
where  is concentration of Al2O3 and
is concentration of Al2O3 and  is concentration of saturated alumina.
is concentration of saturated alumina.
In the cell, overvoltage is also produced on the carbon surface. Because the cathode overvoltage and concentration overvoltage have a little effect on cell voltage [15], it is assumed that the cell overvoltage is only due to the anode overvoltage. According to Tafel equation, anode overvoltage is dependent on the anode current density [16]:
η=a+blg J (7)
where J is anode current density; a=0.5 is Tafel constant; b=0.25 is Tafel slope.
According to the Ohm’s law, Rre and Rov can be calculated.
In the cell, electrolyte is used as solvent, where the alumina dissolves. In general, the distance between the anode bottom surface and liquid aluminum surface is called as anode cathode distance (ACD). Due to the influence of the electromagnetic force and gravity, the liquid aluminum surface is continuous fluctuation, which will cause the variation of the ACD electrolyte resistance [17-19]. In this work, it is assumed that the distance of ACD electrolyte varies with the liquid aluminum fluctuation. The conductivity (κ) of electrolyte can be calculated by the Choudhary’s empirical formula [20]:
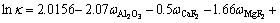
 (8)
(8)
where 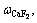

 ,
, are the concentrations of CaF2, MgF2, LiF and NaCl, respectively, n is cryolite ratio (CR).
are the concentrations of CaF2, MgF2, LiF and NaCl, respectively, n is cryolite ratio (CR).
So, the Ohm resistance of the ACD electrolyte can be obtained [13]:
 (9)
(9)
where L is anode-cathode distance; bb is bubble thickness; S is cross sectional area of one anode block group; db is single layer bubble thickness.
The produced bubbles partly attach to the underneath surface of the anode, and partly mix with the electrolyte. All of these bubbles will increase the resistance of the electrolytic circuit. This additional resistance (R_bu) can be calculated as [13]
 (10)
(10)
where fc is the fraction of anode covered by bubbles.
3 Design of mathematical model
The Matlab/Simulink simulation software has been chosen for constructing and simulating the equivalent circuit of the cell. Simulink is a visual simulation tool of the MATLAB, which is the software package used for dynamic system modeling, simulation and analysis, supporting linear and nonlinear systems which are continuous, discrete, and both at the same time, and a variety of sampling frequency systems. It can be used to continuously simulate the cell current based on this equivalent circuit simulation model. As the aluminum electrolysis cell is a coupling system of electric field, magnetic field, thermal field and melt flow field, this simulation is based on the following assumptions: 1) Cell temperature is maintained at 950 °C; 2) Current flowing through the cell is mainly vertical, and the horizontal current is negligible; 3) Liquid aluminum fluctuation will produce sine wave, and cause the change of ACD thickness; 4) Bubbles are produced uniformly on the anode surface.
A 400 kA electrolysis cell was chosen for this study. This type cell has 24 double anode carbon blocks. The simulation model of the equivalent circuit with 24 anode branches has been built with Matlab/Simulink simulation software. Figure 2 shows a three-branch model, which is a part of the 24-branch model. In this model, simulation system includes several software modules, such as control current source, RLC branch and scope. Moreover, it also contains some self-designed modules, such as reaction resistance module (Rr), overvoltage resistance module (Ro), electrolyte resistance module (RACD), bubble resistance module (Rb), and anode resistance module (Ra). According to the Eqs. (3)-(10), the output resistance of these self-designed modules changes with ACD, bubble coverage fraction, concentration of alumina, current, and so on. In addition, the fixed resistance module (r) represents the resistance of anode rod and steel stub, other resistance modules simulate cathode and cathode bar resistance, T is the electrolysis temperature, Al2O3% module shows the concentration of alumina, fc module is the fraction of bubble coverage, and ACD module represents the change of ACD caused by liquid aluminum fluctuation.
Aluminum electrolytic process is a very complex dynamic process. In order to investigate the influence of bubbles on anode current distribution and cell voltage, the cell condition is seen as stable in a short time. It is assumed that the single-layer bubble thickness is 0.5 cm [21], and two layers of bubbles are generated covering on the anode surface.
In industrial production, alumina dissolves in the bath and is continuously consumed. So, the alumina powder needs to be added to the electrolyte. Alumina has a solution-consumption process in the bath. It is assumed that the alumina dissolves quickly in the bath, and the consumption rate is uniformity. The concentration varies between 2%-3%, and the consumption period is 89 [22].

Fig. 2 Schematic diagram of three-branch simulation circuit
According to literature [23], the liquid aluminum fluctuation cycle is about 50 s, and the waveform is in an arc-shaped form. So, it is assumed that liquid aluminum waveform is the standard sine wave and satisfies the following formula:
y=Asin(2πft+θ)+h (11)
where A is the variation amplitude of ACD caused by the liquid aluminum fluctuation; f is the frequency of the liquid aluminum fluctuation; t is time; θ is the initial phase; h is the average height of the ACD.
According to JENSEN et al [24], average ACD is assumed as 4.1 cm in this study. WANG et al [23] pointed out that the fluctuation range of liquid aluminum is 0.9-1.5 cm in traditional cells. The anode size is very large in actual cells, and the liquid aluminum surface is fluctuant, so the ACDs under anode bottom are not the same at different positions. In our model, we see the whole anode as a resistance, the ACD under each anode should be the average ACD of each point at anode bottom. Therefore, the variation amplitude of ACD was supposed at 0.2 cm after lots of calculations. The fluctuation frequencies under different anode blocks were different, and it is assumed that the fluctuation frequencies of 24 branches are around 0.02 Hz [23].
There are many researches about the bubble formation, growth and its movement on the anode surface. Most of these researches [10,11] found that bubble release frequency was 0.3-3 Hz, the fraction of anode surface covered by bubbles was 30%-60%, and the bubbles release was periodic behavior. So, it is assumed that the bubble coverage changes uniformly on the anode surface, the coverage fraction increases evenly within a certain range and the periodic line makes a zigzag [25]. The bubble coverage fraction and release frequency are different under different anode blocks, and the assumption values are given in Table 1.
According to the sampling theorem, the simulation discrete time of 0.1 s was chosen to study all hypothesis frequencies, namely sampling frequency is 10 Hz. And the simulation time was set at 500 s.
4 Results and discussion
4.1 Cell voltage fluctuation and current distribution
In the aluminum electrolysis cell, the anode bubble is an important reason for the oscillation of cell voltage and current distribution. In order to further study the effect of bubble behavior on the cell voltage and current distribution a comparison simulation was studied. In this comparison simulation, it is assumed that the bubble coverage fraction on anode surface remains at 45%. The cell voltage and current simulation data were obtained after running these two comparison models. Figure 3 shows the cell voltage and current going through No. 7 anode carbon block. The black dot curve in Fig. 3 represents the bubble coverage fraction stable model, while the blue curve represents the bubble coverage fraction changing model. The simulation results have a good agreement with the actual situation.
Table 1 Statistical values of 24 anodes current with fraction of bubble coverage varying


Fig. 3 Cell voltage (a) and current going through No. 7 anode carbon block (b) obtained by two comparison models
These simulation data were statistically analyzed. Table 2 provides the statistical results of cell voltage. It is known from Fig. 3 (superior) and Table 2 that, when the bubble coverage fraction is varied, the average cell voltage ( ) decreases by about 11.5 mV, but the fluctuation amplitude (ΔU) increases by about 38 mV. In Fig. 3, the blue curve is more volatile than the black curve, indicating that this curve contains more noise. It can also be seen from the standard deviation (Ud) and the maximum value (UMax is the maximum value and the UMin is the minimum value) that the gas bubble variety will increase cell voltage fluctuation amplitude.
) decreases by about 11.5 mV, but the fluctuation amplitude (ΔU) increases by about 38 mV. In Fig. 3, the blue curve is more volatile than the black curve, indicating that this curve contains more noise. It can also be seen from the standard deviation (Ud) and the maximum value (UMax is the maximum value and the UMin is the minimum value) that the gas bubble variety will increase cell voltage fluctuation amplitude.
Table 2 Statistical values of cell voltage

When the bubble coverage is fixed, the average current through each anode has little difference due to the liquid aluminum fluctuation. Simulation results show that the average currents of different anodes range between 16646.47 and 16681.63 A, and the difference is only 45.16 A, which is very small compared with 16.6 kA current. In addition, all the current statistical parameters of different anodes vary in a very small range.
When the bubble coverage varies, the average currents of different anodes are quite different from each other, all of which are between 16208.86 and 17177.47 A, and the difference is 968.61 A. Table 1 offers the statistical values of 24 anode currents when bubble coverage changes. Figure 3 (inferior) illustrates clearly that the current fluctuation is greater, which is caused by the bubble changing. In Table 1, the standard deviations (Id) and current fluctuation amplitude (ΔI) change more greatly, which shows that gas bubble has a significant effect on anode current distribution.
Figure 4(a) shows comparison of the average current of each anode ( ) and the average fraction of bubble coverage (
) and the average fraction of bubble coverage ( ). It can be intuitively seen that the values of average current are different. The average current probably has an inversely proportional relationship with the bubble coverage fraction. That is, the average bubble coverage fraction increases and the current decreases. With regard to the No. 4 and No. 19 anode current, the bubble coverage is the same, but the current statistical parameters are different, as given in Table 1. This is because bubble release frequency and liquid fluctuation frequency are not the same, which may induce the change of current. Figure 4(b) shows the average current of each anode with the bubble release cycle. The regularity shown in this figure is not so obvious. This may be because the effect of release frequency on current is very little.
). It can be intuitively seen that the values of average current are different. The average current probably has an inversely proportional relationship with the bubble coverage fraction. That is, the average bubble coverage fraction increases and the current decreases. With regard to the No. 4 and No. 19 anode current, the bubble coverage is the same, but the current statistical parameters are different, as given in Table 1. This is because bubble release frequency and liquid fluctuation frequency are not the same, which may induce the change of current. Figure 4(b) shows the average current of each anode with the bubble release cycle. The regularity shown in this figure is not so obvious. This may be because the effect of release frequency on current is very little.

Fig. 4 Comparison between average current ( ) of each anode and average fraction of bubble coverage (
) of each anode and average fraction of bubble coverage ( ) (a) and comparison between average current of each anode and bubble release cycle (b)
) (a) and comparison between average current of each anode and bubble release cycle (b)

Fig. 5 Power spectra of cell voltage (a) and No. 7 current (b) with bubble coverage fraction changing
The frequency spectral analysis method was also used to analyze the simulation signals, as shown in Fig. 5. Figure 5 shows the power spectra of the cell voltage and No. 7 branch current when the bubble coverage changes. In Fig. 5(a), there is one peak at 0.02 Hz, and its power exceeds 200 W, which is consistent with the liquid aluminum fluctuation frequency. Bubble release frequencies all appear between 0-5 Hz, and the maximum power almost reaches 200 W. This illustrates that the bubble has a great influence on the cell voltage. It is also found that all the assumed frequencies can present in this figure. Figure 5(b) shows the power spectrum of No. 7 anode current. In the power spectrum, there are two higher peaks at 0.0176 Hz and 0.288 Hz, which are respectively consistent with the liquid aluminum fluctuation frequency and bubble release frequency. Because the liquid aluminum and bubble release are both regular variation, there is a little noise in Fig. 5(b).
According to the above analyses, both the bubble coverage and bubble release frequency may have some effects on the cell voltage and current distribution. Therefore, this work will further investigate their influence on the cell voltage and current distribution with this simulation model. In the above design model, bubble release frequency and coverage fraction of different anodes are different. In order to facilitate the research, No. 7 anode was chosen as the study object.
4.2 Effect of bubble release frequency
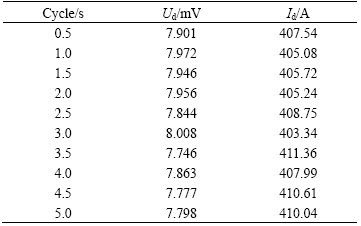
Changing the bubble release frequency of the No. 7 anode branch, meanwhile keeping the bubble coverage at 39%-47%, 10 times simulations were conducted. The release cycles are 0.5, 1.0, 1.5, 2.0, 2.5, 3.0, 3.5, 4.0, 4.5 and 5.0 s, respectively. Ten groups of simulation results were obtained. The average values of the cell voltage and No. 7 anode current were calculated, plotting its graph corresponding to the release cycle, as it is shown in Fig. 6.

Fig. 6 Average values of cell voltage and No. 7 current under different bubble release cycles
Figure 6 shows that cell voltage gradually increases with the increase of bubble release cycle. Namely, when the release frequency increases, the cell voltage decreases. But the increasing trend gradually slows down. It can be seen that the cell voltage increases rapidly from 4.06124 to 4.06154 V with the cycle increasing from 0.5 s (2 Hz) to 2.5 s (0.4 Hz), the voltage increases by about 0.3 mV. When the cycle increases from 2.5 s (0.4 Hz) to 5.0 s (0.2 Hz), the cell voltage increases by only 0.03 mV. As a whole, the maximum difference of the 10 times simulation results is not more than 0.33 mV. The current through No.7 anode gradually decreases, the decreasing trend is also slowing, and the maximum difference of the 10 times simulation results is about 62 A. In addition, according to the fluctuation amplitude in Table 3, the standard deviation of cell voltage mainly decreases with the bubble release cycle increasing. This simulation result is consistent with the research of EINARSRUD and SANDNES [2], which is noted that high frequencies appear to be related to small amplitudes in voltage oscillations. This conclusion was also discussed by KISS et al [7]. In Table 3, the amplitude of No. 7 anode current mainly increases with the decrease of bubble cycle.
Table 3 Standard deviations of cell voltage and No. 7 anode current under different bubble release cycles
4.3 Effect of bubble coverage range
Keeping the No. 7 anode bubble release frequency fixed, increasing the range of bubble coverage, but keeping the average coverage fraction at 45%, six times simulations were carried out. The fluctuation ranges of bubble coverage are 44%-46%, 42%-48%, 40%-50%, 38%-52%, 36%-54% and 34%-56%, respectively. And the variation amplitudes (ΔC) are 2%, 6%, 10%, 14%, 18% and 22%, respectively. Figure 7 shows the changes of cell voltage and No. 7 anode current corresponding to the change of variation amplitude of bubble coverage.
In Fig. 7, when the bubble release frequency is fixed, cell voltage increases with the increase of bubble coverage variation amplitude. When the bubble coverage range is 44%-46%, the average cell voltage is 4.0625 V, and when the coverage range is 34%-56%, the average cell voltage is 4.0628 V, and the value is increased by about 0.3 mV. Meanwhile, the average current of No. 7 anode is reduced from 16582.38 to 16529.35 A, and the value reduces by approximately 53 A. Table 4 shows that standard deviations of cell voltage and No. 7 anode current are both increased as the bubble coverage fluctuation enlarges. This result is also fitted well with the results of KISS et al [10,26] and EINARSRUD and SANDNES [2].

Fig. 7 Average values of cell voltage and No. 7 anode current corresponding to increasing of variation amplitude of bubble coverage (△C)
Table 4 Standard deviations of cell voltage and No. 7 anode current under different bubble coverages

4.4 Effect of bubble thickness
Changing the bubble thickness of No. 7 anode branch, the simulation model was run again. Ten times simulation bubble thicknesses are 0.2, 0.4, 0.6, 0.8, 1.0, 1.2, 1.4, 1.6, 1.8 and 2.0 cm, respectively. The simulation values of average cell voltage and No. 7 anode current are shown in Fig. 8. It is seen that the cell voltage linearly increases with the increase of bubble thickness, while the current decreases. In Table 5, with the increase of bubble thickness, the standard deviation of cell voltage increases, while that of No. 7 anode current increases. This explains that the bubble thickness will increase the fluctuations of the cell voltage and anode current.
4.5 Anode effect
In the aluminum electrolysis production, anode effect (AE) is a common phenomenon. The reduction of alumina concentration will inhibit the electrolysis reaction and gas escaping, so the fraction of bubble coverage on anode surface increases, which will cause the increase in cell voltage and arc discharge. Anode effect will reduce the current efficiency, and have an adverse effect on the production, which is an undesirable phenomenon. With the increase of cell volume, the distribution of alumina concentration in the cell is more difficult to be completely consistent. When alumina concentration decreases somewhere, anode effect may occur locally, resulting in a local effect. The local effect would gradually spread as the time goes, and then the whole cell anode effect occurs. Although several methods based on cell voltage have been developed to predict the anode effect [27,28], they are still difficult to determine whether the anode effect is local anode effect or not. By this simulation model, this study hopes to preliminarily investigate the regulation of cell voltage when local anode effect occurs.

Fig. 8 Average values of cell voltage and No. 7 anode current corresponding to variation of bubble thickness
Table 5 Standard deviations of cell voltage and No. 7 anode current under different bubble thicknesses

Assuming that the No. 7 anode bubble coverage gradually increases, and no energetic chemical change is caused during this process. The simulations were conducted by this model with different bubble coverages. When the anode surface is completely covered by gas bubbles (i.e., bubble coverage is 100%), it is assumed that there is no current going through this anode. The obtained data were processed by linear regression method, and the average values of cell voltage and current were obtained, as shown in Fig. 9.

Fig. 9 Average values of cell voltage and No. 7 current with bubble coverage increasing
In Fig. 9, cell voltage increases with the bubble coverage increasing, and the increasing trend is strengthened. When the coverage reaches 60%, the cell voltage is 4.0750 V, and when it is 75%, the voltage is 4.0968 V. The cell voltage is still in normal fluctuation range. But when the coverage increases to 80%, the cell voltage is 4.1067 V, which exceeds the normal fluctuation range. When the coverage is 100%, the cell voltage is 4.15 V. Meanwhile, the current change is more obvious. The current is 14202 A when the coverage is 60% and the current reduces to 8447 A when the coverage reaches 80%. Therefore, the influence of the bubble coverage on the cell voltage and anode current is very great, especially when the fraction is more than 80%.
The anode effect may begin from one anode surface, and spread to the whole cell. So, we assume that any number of anodes can produce local AE, while the other anodes are still in normal. Of course this is not possible in actual production due to the great redistribution of anode current. The anode is completely covered by the gas bubbles when AE phenomenon appears. Figure 10 shows the plot of average cell voltage when AE phenomenon appears. In Fig. 10, the cell voltage increases as the AE anode number increases. When the AE anode number is less than 16, the cell voltage is less than 8.0 V, which is difficult to determine in normal computer detection. When the AE anode number is more than 16, the cell voltage increases quickly. So if this happened, the whole cell AE is inevitable. It can be inferred that the anode effect detected by computer in the actual production is mainly the whole cell anode effect.

Fig. 10 Relationship between average cell voltage and number of anode appearing AE
5 Conclusions
1) The equivalent circuit model of aluminum electrolysis cell was simulated with the Matlab/Simulink simulation software. The input data were obtained on the basis of actual production process and data suggested in published literature. The simulation result shows that this method is simple and easy to implement.
2) With the simulation model, the gas bubbles influence on the cell voltage and anode current distribution was investigated. The cell voltage will decrease with the bubble release frequency increasing. Higher frequency has a greater effect on the cell voltage oscillation, especially when the frequency is more than 0.4 Hz.
3) When the bubble coverage and bubble thickness increase, the cell voltage increases, and the anode current decreases. When the bubble coverage of one anode block exceeds 80%, the cell voltage may exceed normal fluctuation range.
4) Normal computer detection is difficult to predict the local anode effect, so the detected AE by computer in actual production is mainly the whole cell anode effect, which is further proved by the simulation.
References
[1] ZORIC J, SOLHEIM A. On gas bubbles in industrial aluminium cells with prebaked anodes and their influence on the current distribution [J]. Journal of Applied Electrochemistry, 2000, 30: 787-794.
[2] EINARSRUD K E, SANDNES E. Anodic voltage oscillations in Hall-Heroult cells [C]//Light Metals. San Diego, CA: TMS, 2011: 555-560.
[3] HAUPIN W E. A scanning reference electrode for voltage contours in aluminum smelting cells [J]. Journal of Metals, 1971, 23(1): 46-49.
[4] DOHEIM M A, EL-KERSH A M, ALI M M. Computational modeling of flow in aluminum reduction cells due to gas bubbles and electromagnetic forces [J]. Metallurgical and Materials Transactions B, 2007, 38(2): 113-119.
[5] KUANG Z, THONSTAD J. Current distribution in aluminum electrolysis cells with Soderberg anodes. Part 1: Experimental study and estimate of anode consumption [J]. Journal of Applied Electrochemistry, 1996, 26: 481-486.
[6] ZORIC J, ROUSAR I, KUANG Z. Current distribution in aluminum electrolysis cells with Soderberg anodes. Part 1: Mathematical modeling [J]. Journal of Applied Electrochemistry, 1996, 26: 795-802.
[7] KISS, L I, PONCSAK, S, ANTILLE J. Simulation of the bubble layer in aluminum electrolysis cells [C]//Light Metals. San Francisco, CA: TMS, 2005: 559-564.
[8] PONCSAK S, KISS L, TOULOUSE D, PERRON A, PERRON S. Size distribution of the bubbles in the  cells [C]//Light Metals. San Antonio, TX: TMS, 2006: 457-461.
cells [C]//Light Metals. San Antonio, TX: TMS, 2006: 457-461.
[9] RICHARDS N, GUDBRANDSEN H, ROLSETH S, THONSTAD J. Characterisation in the fluctuation in anode current density and bubble events in industrial reduction cells [C]//Light Metals. San Diego, CA: TMS, 2003: 315-322.
[10] KISS L I, PONCSAK S. Effect of the bubble growth mechanism on the spectrum of voltage fluctuations in the reduction cell [C]//Light Metals. Seattle, WA: TMS, 2002: 217-223.
[11] CHENUNG C, MENICTAS C, BAO J, SKYLLAS-KAZACOS M, WELCH B J. Frequency response analysis of anode current signals as a diagnostic aid for detecting approaching anode effects in aluminum smelting cells [C]//Light Metals. San Antonio, TX: TMS, 2013: 887-892.
[12] XUE J, OYE H A. Bubble behaviour-cell voltage oscillation during aluminium electrolysis and the effects of sound and ultrasound [C]//Light Metals. San Francisco, CA: TMS, 1995: 265-271.
[13] FENG Nai-xiang. Aluminum electrolysis [M]. Beijing: Beijing Chemical Industry Press, 2006: 57-60. (in Chinese)
[14] HAUPIN W. Interpreting the components of cell voltage [C]//Light Metals. San Antonio, TX: TMS, 1998: 531-537.
[15] DRENGSTIG T, KOLAS S, STORE T. The impact of varying conductivity on the control of aluminum electrolysis cells [C]//Light Metals. Seattle, WA: TMS, 2002: 205-216.
[16] ZORIC J, ROUSAR I, THONSTAD J. Mathematical modelling of industrial aluminium cells with prebaked anodes, Part I: Current distribution and anode shape [J]. Journal of Applied Electrochemistry, 1997, 27: 916-927.
[17] FREDERIC J, LELIEVRE T, LE C. Metal pad roll instabilities [C]//Light Metals. Seattle, WA: TMS, 2002: 483-487.
[18] ANTILLE J, KAENEL R V. Using a magnetohydrodynamic model to analyze pot stability in order to identify an abnormal operation condition [C]//Light Metals. Seattle, WA: TMS, 2002: 477-482.
[19] WANG Y, ZHANG L, ZUO X. Fluid flow and bubble behavior in the aluminum electrolysis cell [C]//Light Metals. San Francisco, CA: TMS, 2009: 581-586.
[20] CHOUDHARY G. Electrical conductivity for aluminum cell electrolyte between 950-1025 °C by regression equation [J]. Journal of the Electrochemical Society, 1973, 120(3): 381-383.
[21] COOKSEY M A, TAYLOR M P, CHEN J J J. Resistance due to gas bubbles in aluminum reduction cells [J]. JOM, 2008, 60(2): 51-57.
[22] LI Xian, LIU Min-zhang. Effect of adjusting feeding interval on technical parameters of aluminium electrolysis [J]. Light Metals, 2011: s228-s230. (in Chinese)
[23] WANG Z, FENG N, PENG J. Study of surface oscillation of liquid aluminum in 168 kA aluminum reduction cells with a new type of cathode design [C]//Light Metals. Seattle, WA: TMS, 2010: 485-488.
[24] JENSEN M, KALGRAF K, NORDBO T. ACD measurement and theory[C]//Light Metals. San Francisco, CA: TMS, 2009: 455-459.
[25] WANG X, TABEREAUS T A. Anodic phenomena-observations of anode overvoltage and gas bubbling during aluminum electrolysis [C]//Light Metals. Nashville, TE: TMS, 2000: 239-247.
[26] KISS L I. Transport processes and bubble driven flow in the Hall-Heroult cell [C]//Proceedings of the Fifth International Conference on CFD in the Process Industries. Melbourne, Australia: CSIRO, 2006: 13-15.
[27] SULMONT B, FARDEAU S, BARRIOZ E, MARCELLIN P. The new development of the ALPSYS system related to the management of anode effect impact [C]//Light Metals. San Antonio, TE: TMS, 2006: 325-329.
[28] COSTA F D, PAULINO L, BRAGA C, RAMADA R, SOUSA I. Computer algorithm to predict anode effects events [C]//Light Metals. Orlando, FL: TMS, 2012: 655-656.
王永良1,铁 军2,涂赣峰1,孙树臣1,赵仁涛2,张志芳2
1. 东北大学 材料与冶金学院,沈阳 110819;
2. 北方工业大学 机械与材料工程学院,北京 100144
摘 要:建立一种研究气泡对槽电压波动影响的方法,该方法将整个电解槽等效为一个电阻电路,并利用Matlab/Simulink仿真软件建立等效电路的仿真模型进行动态仿真研究,从而获得不同气泡状态下槽电压和阳极电流的时间序列数据,利用频谱和统计分析方法对这些数据进行分析。结果显示,较高的气泡释放频率对槽电压波动的影响更大,当一组阳极表面气泡覆盖率超过80%时,槽电压可能超出正常的波动范围。仿真结果证实了在实际生产中计算机监测到的阳极效应主要是全槽的阳极效应。
关键词:铝电解;等效电路;气泡;槽电压;阳极效应
(Edited by Xiang-qun LI)
Foundation item: Project (2012BAE08B09) supported by the National Key Technology R&D Program of China
Corresponding author: Jun TIE; Tel: +86-10-88803297; E-mail: tiejun67@263.net
DOI: 10.1016/S1003-6326(15)63609-3

