
Filling and solidification of TiAl melt in centrifugal field
SHENG Wen-bin(盛文斌) Department of Mechanical Engineering, Shandong University of Technology, Zibo 255049, China
Received 10 April 2006; accepted 25 April 2006
Abstract: A model was established based on the combination of the equation of continuity, the equation of conservation of momentum and the equation of general energy to describe the filling and solidification of TiAl melt by permanent mold centrifugal casting. The model was solved numerically and the filling and solidification processes in the centrifugal field were discussed. The results indicate that the centrifugal field essentially influences the filling and solidification processes of TiAl melt. The melt will first fill the cavity along the back boundary until it reaches the end. After the end is fully filled, the whole cavity will be filled gradually by the way that free surface of the melt moves towards the entrance, hence the entrance is the last part to be filled. Furthermore, the mechanism by which internal defects can be formed in centrifugally cast TiAl components were interpreted.
Key words: TiAl melt; filling and solidification; model; centrifugal field; defects
1 Introduction
TiAl-based alloys have been considered an excellent candidate materials for automotive valve applications due to their low density and high-strength at high temperatures [1, 2]. Based on the demand for a high volume and low cost manufacturing method, permanent mold casting exhibits the most potential for TiAl valves [3-5]. However, the combination of the low density (about 3.9 g/cm3) of TiAl-based alloys and the powerful heat conduction of the permanent mold imply the difficulty in fully filling and enough feeding during the solidification.
Generally, feeding of the castings depends on the mass of the molten metal in a static (or gravity) casting system. For light metals, an assistant force field is sometimes employed to improve the feeding, such as a magnetic field for aluminum alloys and a centrifugal field for titanium alloys [4, 6]. In the past decades, a centrifugal field has been extensively applied to the manufacture of cast tubes, in which the tube axis always coincides with the rotation axis. Recently, the centrifugal field has been also applied to some advanced materials, such as nonferrous alloys [6, 7], ceramics [8] and composites [9]. However, for centrifugal casting TiAl valves, the horizontal cavity is a certain distance away from the vertical axis and rotates round it, which leads to an entirely different filling and solidification process compared with that in the static system. Some characteristics, such as off-center shrinkage pores, were reported in centrifugally cast TiAl valves [5, 10].
This work models the centrifugal casting of TiAl alloy to reveal the filling and solidification in a centrifugal field, as well as the formation of internal defects that can exist in the castings.
2 Modeling of centrifugal casting process
For the permanent mold centrifugal casting of TiAl valves[3], the metallic mold, whose material was niobium alloy or steel, was fixed in a vacuum chamber containing an induction skull melting (ISM) furnace. The mould consisted of several layers, each with some cavities assembled radially. Molten metal is poured under gravity from the tilting crucible, subsequently impacts the mold bottom and enters the pre-heated mold at a rotation speed of ω0 (r/min), as shown in Fig.1. The melt will fill the cavity with an increasing velocity along the axial (x-axis) direction due to the effect of the centrifugal force. At the same time, the Coriolis force that horizontally points to the back wall of the cavity makes the melt move towards the opposite direction of the y-axis. The z-axis points upwards in the coordinate system.

Fig.1 Schematic diagram of centrifugal cast TiAl valve
The melt will fully fill the valve head owing to its mushroom configuration. So, the flow influenced by the centrifugal field is only restricted in the cavity of the valve stem, which is similar to that in a horizontal tube. As soon as the melt enters the stem cavity, its cross sectional area will keep decreasing to maintain a continuous filling due to the increasing axial velocity. The entrance length L0 denotes the distance from the rotating axis to the valve head/stem region where the filling velocity is the entrance velocity v0. The stem cavity is treated as a cylinder whose radius and length are R and L (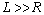 ), respectively.
), respectively.
Furthermore, it was assumed that: 1) the incompressible molten metal (ρm is constant) is in a fully developed steady flow state and fills the stem cavity continuously; 2) the kinematic viscosity vm of the melt is a constant; 3) the loss by friction during the filling process is neglected. Therefore, the centrifugal filling and solidification process of molten TiAl is modeled by the combination of the equation of continuity, the equation of conservation of momentum (N-S) and the equation of general energy, corresponding to Eqns.(1), (2) and (3), respectively.
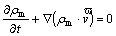 (1)
(1)
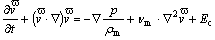 (2)
(2)
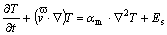 (3)
(3)
where t, 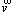 , T and p represent time, velocity, temperature and pressure, respectively; vm and αm are respectively the kinematic viscosity and the thermal diffusivity of molten TiAl; Ec denotes the composition of accelerations and consists of three terms: the gravitational acceleration, the centrifugal acceleration and the Coriolis acceleration. The gravitational force is a constant, while the centrifugal force and Coriolis force are in direct proportion to the distance from the selected location to the rotation axis and the filling velocity, respectively; Es is an energy term, such as the latent heat released during the solidification.
, T and p represent time, velocity, temperature and pressure, respectively; vm and αm are respectively the kinematic viscosity and the thermal diffusivity of molten TiAl; Ec denotes the composition of accelerations and consists of three terms: the gravitational acceleration, the centrifugal acceleration and the Coriolis acceleration. The gravitational force is a constant, while the centrifugal force and Coriolis force are in direct proportion to the distance from the selected location to the rotation axis and the filling velocity, respectively; Es is an energy term, such as the latent heat released during the solidification.
In the selected horizontal axial section, difference format of the description equations can be established by resorting to the finite-difference technique. Here, u and v are the velocities in the x and y directions respectively. At the melt/cavity interface, the combined effect of the centrifugal field and the incomplete filling near the entrance results in uncertain boundary conditions for the pressure term p. It is obviously different from that in the gravitational casting system, in which the boundary conditions for p can be considered as a constant determined by the mass or the height of molten melt. Therefore, the stream function ψ(x, y) and the eddy function ξ(x, y) were utilized as a substitution for the pressure term p and hence Eqns.(1) and (2) become
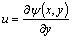 (4)
(4)
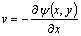 (5)
(5)
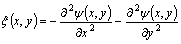 (6)
(6)
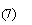
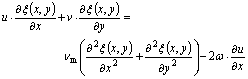
The rectangular section was meshed with uniform step Δx in the -direction and variational steps Δy in the y-direction, and then the difference equations on the control volume (i, j) are
-direction and variational steps Δy in the y-direction, and then the difference equations on the control volume (i, j) are
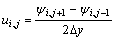 (8)
(8)
 (9)
(9)
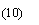
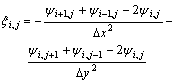
 (11)
(11)
The general energy equation on unit (i, j) becomes
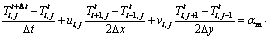
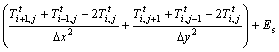 (12)
(12)
Before the cavity is fully filled, heat is transported by convection in steady state. In this case, Eqn.(12) becomes
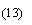
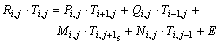
Otherwise, heat is transported by conduction in unsteady state. Equation (12) becomes
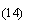

In Eqns.(13) and (14):
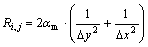
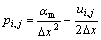
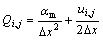
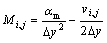
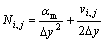
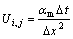
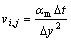
3 Results and discussion
The model was numerically solved using the finite-difference technique. Fig.2 shows the variations of velocity versus filling length in different cross sections (L0+10, L0+35, L0+65, L0+90 mm away from the rotation axis, respectively) at a rotation speed of 300 r/min. At the entrance, the melt near the axis shows the maximum filling velocity, where the shear stress tends to be zero. The maximum shear stress appears in the melt bordering
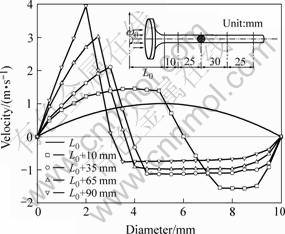
Fig.2 Distribution of velocities in different cross sections at rotation speed of 300 r/min
upon the front boundary. The stress is equal to that existing in the melt next to the back boundary and points in the reverse direction (one is positive and the other is negative).
It is concluded that the variations of velocity and shear stress at the cavity entrance are similar to those in steady-state flow in a fully-filled tube. According to the velocity distribution, the cross section farther away from the rotation axis exhibits a higher maximum velocity in the x-axis direction, but a lower one in the negative direction. The location with the higher maximum velocity tends to approach the back boundary due to the effect of the Coriolis force. Therefore, the centrifugal filling process can be summarized as the melt filling the cavity with a higher and higher axial velocity that is closely related to some factors, such as L0, v0 and ω0. Simultaneously, the Coriolis force impels it towards the back wall of the tube. Due to the increasing axial filling velocity, the cross sectional area keeps decreasing to ensure the continuity of the filling process. As a result, the cavity will not be filled completely before the melt reaches the cavity end. As soon as the cavity end has been fully filled, the free surface begins to move from the end to the entrance so that the whole cavity is fully filled.
In general, solidification models assume that casting system is in a uniform field, such as the gravitational field, and thus the starting temperature distributions of the melt and the mold are treated as the melting temperature and the environmental temperature, respectively [11, 12]. In this research, the model for TiAl valve was established with emphasis on the centrifugal field. Once the cavity has been fully filled, the temperature distribution is regarded as the initial temperature field for the following solidification process. At a rotation speed of 300 r/min, the temperature distributes in the chosen horizontal section at times of 19.445 and 1 412.300 s, respectively, shown in Fig.3. The results show that a sharp decrease in temperature occurs in the regions bordering upon the front, back and end boundaries due to the powerful heat conduction to the metallic mold at the beginning of solidification. In addition, the melt solidifies in a short time about 3.475 s, which leads to an easy understanding on that the centrifugal field is necessary for an enough feeding.
It is confirmed that the centrifugal field shows an obvious effect on the final location of micro shrinkage porosities in the valve stem characterized by the off-center distribution instead of the central distribution in the gravitational field [3]. The formation of off-center porosity must be closely related to the temperature variation during centrifugal filling process. As shown in Fig.4, upside and downside curves respectively represent the temperature variation in melt bordering upon the front
Fig.3 Temperature fields in selected section at different times at rotation speed of 300 r/min: (a) 19.455 s; (b) 1 412.300 s
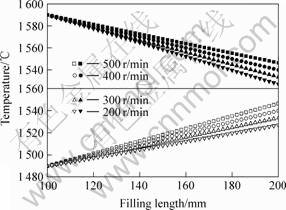
Fig.4 Temperature distribution at cavity frontal and back boundaries in initial temperature fields
and back boundaries when the cavity fully fills at rotation speeds of 200, 300, 400 and 500 r/min. It can be seen that the unsymmetrical feature of the initial temperature distribution in the selected horizontal section leads to continuous unsymmetrical temperature variations during the following solidification.
4 Conclusions
A mathematical model with an emphasis on the effect of the centrifugal field is established to describe the process of casting TiAl valve in a metallic mold. Furthermore, the centrifugal filling and solidification processes in a horizontal tube are summarized to interpret the mechanism by which internal defects are formed in centrifugal castings.
References
[1] DIMIDUK D M, MIRACLE D B, WARD C H. Development of intermetallic materials for aerospace systems [J]. Mater Sci Tech, 1992, 8(3): 367-375.
[2] SUN J, HE Y H, WU J S. Characterization of low-temperature superplasticity in a thermomechanically processed TiAl based alloy [J]. Materials Science and Engineering A, 2002, 329-331: 885-890.
[3] BLUM M, CHOUDHURY A, SCHOLZ H, JARCZYK G. Properties of low cost TiAl automotive valves produced by cold wall induction melting and permanent mold centrifugal casting [A]. Gamma Titanium Aluminides [C]. The Minerals, Metals & Materials Society, 1999. 35-39.
[4] WANG Y, WANG J N, YANG J, ZHANG B. Control of a fine-grained microstructure for cast high-Cr TiAl alloys [J]. Materials Science and Engineering A, 2005, 392: 235-239.
[5] XIE C M. Development and application of titanium alloy investment casting technology [A]. Proceedings of the China-Japan Investment Conference on Foundry Engineering [C]. Beijing, 1994. 37-44.
[6] ZHANG J, FAN Z, WANG Y, ZHOU B, Hypereutectic aluminium alloy tubes with graded distribution of Mg Si particles prepared by centrifugal casting [J]. Materials and Design, 2000, 21: 149-154.
[7] WU X H, HU D. Microstructural refinement in cast TiAl alloys by solid state transformations [J]. Scripta Materialia, 2005, 52: 731-734.
[8] Steenkamp G C, Neomagus H W, Krieg H M, Keizer K. Centrifugal casting of ceramic membrane tubes and the coating with chitosan [J]. Separation and Purification Technology, 2001, 25: 407-412.
[9] Yoshimi W, Akihiro K, Koichi M. Particle size distributions in functionally graded materials fabricated by the centrifugal solid-particle method [J]. Composites Sci Tech, 2002, 62: 881-885.
[10] Jones P E, Eylon D. Effects of casting conditions on microstructure of permanent mold and investment cast Ti-47Al-2Nb-2Cr [A]. The Eighth World Conference on Titanium [C]. UK, 1995. 225-232.
[11] AGHAL S, THOMAS M, COURET A. Structural transformations activated during the formation of the lamellar microstructure of TiAl alloys [J]. Intermetallics, 2005, 13: 1008-1013.
[12] Choi J K, Hong C P. Computer simulation of solidification in casting process-state of art in Korea [A]. Modeling of Casting and Solidification Process-I [C]. 1991. 337-343.
(Edited by LI Xiang-qun)
Foundation item: Project(4040-304019) supported by Shandong University of Technology of China
Corresponding author: SHENG Wen-bin; Tel: +86-533-2786801; Fax:+86-533-2786910; E-mail: wbsheng@sdut.edu.cn