改进GTDM-NE模型对我国能源需求规律分析
于凤玲1, 2,陈建宏1,周扬1,周汉陵1
(1. 中南大学 资源与安全工程学院,湖南 长沙,410083;
2. 五邑大学 经济管理学院,广东 江门,529020)
摘要:为了探求能源需求与各主要影响因素之间的关系及规律,通过对近年来我国能源需求量以及各影响因素指标的数据统计分析,建立基于改进灰靶决策及非等距(GTDM-NE)预测模型的能源需求规律模型体系。首先对能源需求的各影响因素进行预测,然后根据预测结果,对历年的各影响因素的灰色测度进行计算;其次,根据计算结果对影响因素进行改进灰靶决策分析,并将分析结果与能源需求量对应;最后,利用改进的GTDM-NE模型建立能源需求量与影响因素之间的规律关系式,并且利用这关系式对能源需求量进行预测与分析。研究结果表明:用GTDM-NE模型对能源需求量进行短期预测结果较精确。
关键词:能源;灰靶决策;非等距
中图分类号:TK9 文献标志码:A 文章编号:1672-7207(2014)09-3288-07
Energy demand law analysis of China based on improved GTDM-NE model
YU Fengling1, 2, CHEN Jianhong1, ZHOU Yang1, ZHOU Hanling1
(1. School of Resources and Safety Engineering, Central South University, Changsha 410083, China;
2. School of Economics & Management, Wu Yi University, Jiangmen 529020, China)
Abstract: In order to explore the relationship and law between the energy demand and the major influencing factors, through the analysis of the recent years statistics data of Chinese energy demand and impact indicators, the energy demand system model was established based on the improved grey target decision-making (GTDM) theory and non-equidistant (NE) model. Firstly, the influencing factors on the energy demand were forecasted. Secondly, according to the predicted results, the influencing factors of every year were considered in grey measure calculation. The improved grey target decision was analyzed, and the results were corresponded to the energy demand. The law between the energy demand and the impact of factors was revealed using the non-equidistant forecast model and the amount of energy demand was forecasted and analyzed. The results show that the GTDM-NE model used to predict the energy demand in short time is more accurate than other ways.
Keywords: energy; demand; grey target decision-making; non-equidistant
能源是人类生存、社会进步与经济发展不可或缺的基础性物质,它对社会发展与人民生活水平提高起重要作用。然而,由于经济快速发展,人口增加,对能源的需求量越来越大,能源的供需矛盾日益突出:因此,对能源需求内在规律进行分析,对能源需求量的预测以及能源进行合理配置都具有重要的现实意义。对能源需求预测常见的模型有灰色预测模型[1]、神经网络预测模型[2]、群智能优化预测模型[3]以及趋势外推[4]等模型。由于能源需求系统的复杂性,影响能源需求量的因素很多,各影响因素之间在量纲、物理意义及对能源需求的影响都不一致,且目前还没有成熟的、完全量化的理论计算公式。针对以上问题,本文作者利用改进灰靶决策理论[5-7]与非等距预测模型[8-9]相结合的方法(GTDM-NE)来预测我国能源需求规律。利用改进灰靶决策将各影响因素指标趋势一致与去量纲化,并由此计算历年来各影响因素指标与理论靶心的靶心距,构建符合数据特征规律的非等距预测模型,得到各影响因素与能源需求量之间的规律。改进后的灰靶决策理论通过灰色测度计算生成效果向量,完全摆脱了人为主观因素的干扰,使计算过程更加科学;而非等距预测模型则突破了以往趋势化判定以及智能预测等模型以等距年份为单一自变量的不足。
1 能源需求规律分析系统建模
1.1 影响因素分析
能源需求系统是一个复杂系统,受到多种因素的影响和制约。根据相关研究,对能源需求量产生影响的因素主要有如下几种[10-11]。
1) 人口数量。人口是社会系统中最基本的因素, 能源是人类赖以生存的基础, 人口数量直接影响着能源的总需求量。但城镇居民与农村居民在生产生活过程中对能源的需求能力不同,在进行能源需求分析时,需要区别对待城镇人口数量X1和农村人口数量X2。
2) 国内生产总值(GDP)。国内生产总值对能源需求的影响归根结底是经济发展对能源需求的影响。随着国内生产总值的增加、经济的发展、大量新工业新企业的建立,能源需求量也会随之增加。国内生产总值也是影响能源需求的一个非常重要的因素。国内生产总值包括第一产业生产总值X3、第二产业生产总值X4、第三产业生产总值X5。对于各产业而言,能源消耗指数相差较大,因此,在能源需求量的建模与分析过程中也应将三大产业进行区分对待。
3) 能源加工及转换效率X6。随着科学技术的进步,尤其是能源领域的科技进步,会导致能源加工及转换效率提高,这样也将会对能源的需求总量产生影响。
1.2 改进灰靶决策分析
影响能源需求的因素很多,但各个因素的影响程度不尽相同,有些因此指标越大,所反映的能源需求量也就越大,这些指标有X1,X2,X3,X4和X5;而X6越大,所反映的能源需求量反而越小。为将各影响因素指标对能源需求量的影响趋势归一化,采用灰色效果测度进行测算,对于指标X1,X2,X3,X4和X5采用灰色上限效果测度进行处理:
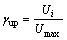 (1)
(1)
而对于指标X6采用灰色下限效果进行测度处理:
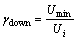 (2)
(2)
其中:Umax,Umin和Ui分别为能源需求量各同类影响因素指标集合{Ui}中最大值、最小值以及一般值。经过灰色效果测度处理后,各因素指标测度越大,所反映的能源需求也就越大。将各因素指标去量纲化与归一化。在计算灰色效果测度时,为确保得到的能源需求规律在一定年份内的适用性,必须推断确定未来若干年内各因素指标的取值范围,预测推断的方法可采用灰色单变量预测模型GM(1,1)和Verhulst模型(包括微分Verhulst模型与差分Verhulst模型)等进行预测。
对于能源需求影响因素,各指标因素历年的数据经过灰色效果测度后的值就是局势sij在指标k下的具体效果值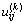 ,由此得到历年能源需求影响因素在局势sij下的效果向量:
,由此得到历年能源需求影响因素在局势sij下的效果向量:
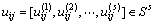 (3)
(3)
其中:Ss为s维超平面区域的决策灰靶,
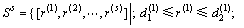
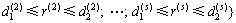 (4)
(4)
决策灰靶在一般情况下都为S维空间内的类似于球形的灰靶,球形灰靶的一般模型为
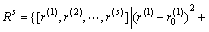
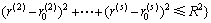 (5)
(5)
靶心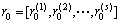 即为历年能源需求量影响因素测度中所反映的理想状态下的极限(最小或最大)能源需求量灰色效果测度向量。年份i的能源需求影响因素灰色效果测度向量
即为历年能源需求量影响因素测度中所反映的理想状态下的极限(最小或最大)能源需求量灰色效果测度向量。年份i的能源需求影响因素灰色效果测度向量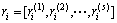 距离靶心r0的靶心距
距离靶心r0的靶心距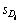 为:
为:
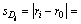
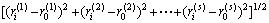 (6)
(6)
计算式(6)中的靶心距时,实际上是将各影响因素对能源需求的影响同等对待,但是,实际上,不同因素对能源需求的影响必然存在差异,因此,在计算靶心距时,将各影响因素对能源需求影响的差异也考虑在内才是合理的。改进后的靶心距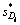 的计算公式如下:
的计算公式如下:
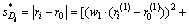
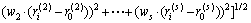 (7)
(7)
式(7)由于添加了权重,实际上已经不再是距离计算公式,但是,式(7)很好地考虑了各影响因素对能源需求影响的差异性,而且其计算公式与距离计算公式极为相似,因此,本改进模型将式(7)视为改进后的靶心距计算公式。靶心距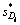 反映了年份i的能源需求量影响因素灰色效果测度向量ri与理想最优灰色效果测度向量r0的偏离程度,
反映了年份i的能源需求量影响因素灰色效果测度向量ri与理想最优灰色效果测度向量r0的偏离程度,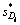 越大,反映的对能源的需求量也就越大。
越大,反映的对能源的需求量也就越大。

图1 改进灰靶决策球形模型
Fig. 1 Improved spherical model of grey target decision-making
1.3 非等距预测分析
对历年能源需求量的影响因素指标进行灰色效果测度,从而建立灰色效果测度向量。再以这些测度向量的改进灰靶决策的靶心距作为自变量,以相应的历年能源需求量作为因变量建立非等距预测模型,对能源需求量规律进行分析。非等距预测模型的最大特点在于由于自变量的非等距特征,导致无法直接进行预测分析,需要构造背景值,将非等距的自变量转换为等距的自变量,然后建模进行预测。
本模型采用最小二乘法进行非等距自变量的等距关系转换。单位时段差系数修正法利用插值法将非等距的自变量转换为等距的自变量的过程中,只考虑了代数意义上的差值最小的方式,而最小二乘法考虑了在空间中的自变量向量的代数拟合。除考虑差值最小外,还考虑到残差平方和最小,考虑更加合理,精度更高。非等距原始序列为

其中:X(0)(Pi)为因变量;Pi为靶心距即自变量。设定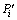 为等距序列,则有
为等距序列,则有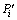 =m0+m1i(其中i∈N,m0与m1为待定系数),且要求
=m0+m1i(其中i∈N,m0与m1为待定系数),且要求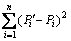 最小,这样,就可以利用最小二乘法的线性拟合模型进行求解,得到m0和m1,进而得到
最小,这样,就可以利用最小二乘法的线性拟合模型进行求解,得到m0和m1,进而得到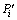 ,而X(0)(
,而X(0)(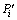 )值则可根据X(0)(Pi)进行插值计算求得。得到转换后的等距原始序列为
)值则可根据X(0)(Pi)进行插值计算求得。得到转换后的等距原始序列为

根据等距的原始数据序列,即可参照各类单阶单变量灰色预测模型进行预测求解。选择最合理精度最高的预测模型为能源需求量的规律公式。对于任意一年的能源需求量影响因素灰色效果测度向量的改进灰靶决策的靶心距Pi,将其代入规律公式即可求得相应年份的能源需求量。常用的单阶单变量灰色预测模型如下。
1) GM(1,1)模型[12-13]。等时间间距统计出前期非负序列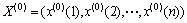 和
和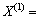
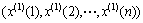 为
为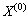 的1-AGO序列。而
的1-AGO序列。而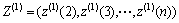 为
为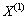 的紧邻均值生成序列。其中:
的紧邻均值生成序列。其中:
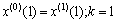 (8)
(8)
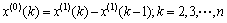 (9)
(9)
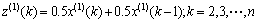 (10)
(10)
若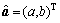 为GM(1,1)模型的参数列,且有
为GM(1,1)模型的参数列,且有
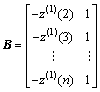 ,
, (11)
(11)
则GM(1,1)模型的最小二乘估计参数列为
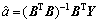 (12)
(12)
则有
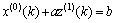 (13)
(13)
为GM(1,1)模型。
2) 微分Verhulst模型[14-15]。设原始数据序列为: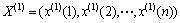 ,则有X(1)的1-IAGO序列
,则有X(1)的1-IAGO序列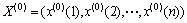 为:
为:
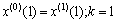 (14)
(14)
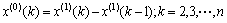 (15)
(15)
紧邻均值生成序列如式(10)所示。若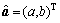 为微分Verhulst模型的参数列,且有
为微分Verhulst模型的参数列,且有
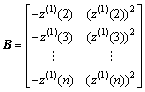 ,
,
则
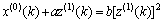 (16)
(16)
为微分Verhulst模型。
3) 差分Verhulst模型[16-17]。设原始数据序列为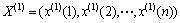 ,则有X(1)的1-IAGO序列
,则有X(1)的1-IAGO序列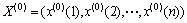 ,紧邻均值生成序列如式(10)所示。若
,紧邻均值生成序列如式(10)所示。若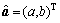 为差分Verhulst模型的参数列,且有
为差分Verhulst模型的参数列,且有
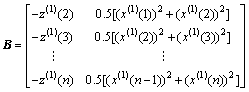

则
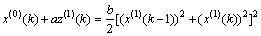 (17)
(17)
为差分Verhulst模型。
对以上3种模型的计算精度进行比较,选取精度最高的模型进行最终预测。精度比较包括平均相对误差比较、残差平方和比较和后验差检验比较。系统建模流程见图2。
2 能源需求规律分析与计算
2.1 灰色效果测度分析
将2000—2011年我国能源需求量E及其影响指标的统计数据收集归纳整理(数据来源于2001—2012年《中国统计年鉴》和《中国能源统计年鉴》)。由整理的数据可以看出:X1,X3,X4和X5都是随着年份推移而稳步增加;X6随着时间呈波动上升;而X2则是随着年份推移而逐渐减少,能源需求量则随着年份推移而稳步增加。
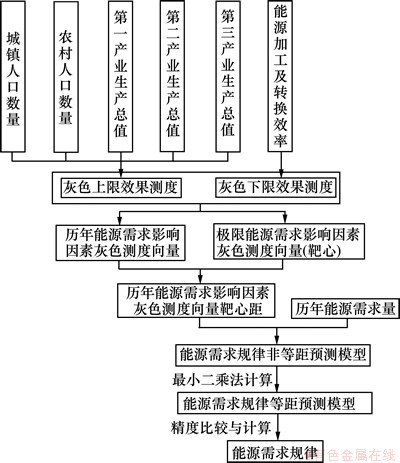
图2 系统建模流程
Fig. 2 System modeling process
在能源需求的各影响因素中,采用灰色上、下限效果测度进行处理后,为使本模型得到的能源需求模型在未来一段时间仍能适用,对于进行灰色上限效果测度的上限值Umax以及进行灰色下限效果测度的下限值Umin的确定要考虑各指标数据在未来一段时间数值变化。为此,对各指标采用单阶单变量的灰色预测模型GM(1,1)模型进行预测。预测得到2000—2015年的各指标。根据历年的能源需求量影响因素值及其范围,得到能源需求影响因素统计数据的灰色效果测度见表1。
通过灰色效果测度,将原本量纲不同的各影响因素数据去量纲化,而且使其趋势一致,更加便于加成运算。灰色效果测度越大,则表明对能源的需求也就越大。本文运用2000—2010年的相关数据研究能源需求规律,然后,根据规律预测2011—2015年的能源需求量。由表1可知:在2000—2010年,理想中的能源需求量最小时的灰色效果测度向量为(0.571 1,0.830 2,0.212 8,0.112 1,0.090 0,0.947 6)。
2.2 改进灰靶决策分析
根据式(7),在计算改进的靶心距时,需要首先根据各影响因素对能源需求影响的重要程度确定权重。本文尝试以灰色关联度[18-19]对客观权重进行确定,以避免主观因素的干扰。灰色关联度的具体计算步骤参考文献[19],归一化权重公式为: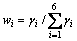 。计算得到6个影响因素Xi (i=1, 2,…,6)分别与能源需求量之间的灰色关联度γi(i=1, 2, …, 6)以及将灰色关联度进行归一化处理,得到各影响指标的权重wi(i=1, 2, …, 6)如表2所示。
。计算得到6个影响因素Xi (i=1, 2,…,6)分别与能源需求量之间的灰色关联度γi(i=1, 2, …, 6)以及将灰色关联度进行归一化处理,得到各影响指标的权重wi(i=1, 2, …, 6)如表2所示。
表1 灰色效果测度
Table 1 Grey effect measurements
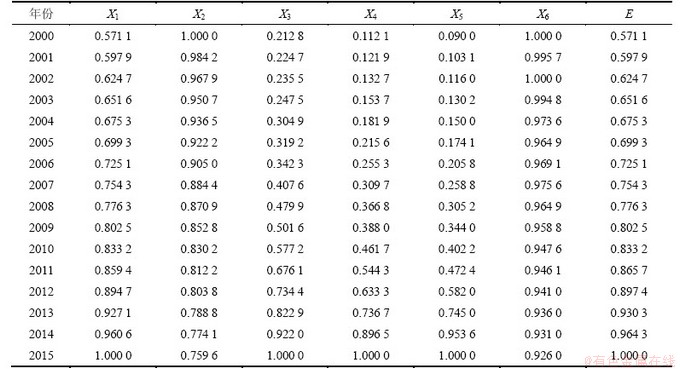
表2 关联度和指标权重
Table 2 Correlation coefficients and weights of indicators
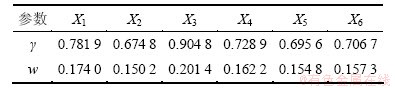
根据灰色关联度的比较结果,可知γ3>γ1>γ4>γ6>γ5>γ2。可见:第一产业对能源需求量的影响最大,城镇人口数量对能源需求的影响次之,而农村人口对能源需求的影响最小。
2.3 非等距预测模型分析
根据表1及表2所示结果并结合式(7),得到各年份能源需求影响因素灰色效果测度向量靶心距。进一步根据靶心距及其对应的能源需求量,统计得到能源需求规律非等距预测模型分析的基础数据,见表3。
根据表3,得到非等距预测的数据非等距步长序列P以及原始数据序列X(P)。对P序列利用最小二乘法进行拟合,拟合得到线性拟合的公式为
表3 非等距预测基础数据
Table 3 Basic data of non-equidistant forecast

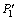 =-0.000 4+0.008 9i
=-0.000 4+0.008 9i
即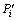 的序列为:
的序列为: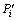 =(0.008 5, 0.017 4, 0.026 3, 0.035 2, 0.044 1, 0.053 0, 0.061 9, 0.070 8, 0.079 7, 0.088 6, 0.097 5)。根据P序列与
=(0.008 5, 0.017 4, 0.026 3, 0.035 2, 0.044 1, 0.053 0, 0.061 9, 0.070 8, 0.079 7, 0.088 6, 0.097 5)。根据P序列与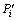 的距离,以X(P)为基础,进行线性插值计算得到:
的距离,以X(P)为基础,进行线性插值计算得到: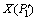 =(-1 338 719, -535 494, 177 701.8, 217 890.3, 246 189.8, 263 812.9, 275 242.6, 283 458.1, 288 928.1, 299 738.4, 310 815.9)。由于现行插值得到的
=(-1 338 719, -535 494, 177 701.8, 217 890.3, 246 189.8, 263 812.9, 275 242.6, 283 458.1, 288 928.1, 299 738.4, 310 815.9)。由于现行插值得到的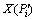 有负值,将负值去掉后得到用来进行灰色预测的原始数据序列为:X(Pi*)= (177 702, 217 890, 246 190, 263 813, 275 243, 283 458, 288 928, 299 738, 310 816)。根据X(Pi*),建立GM(1,1)模型、微分Verhulst模型以及差分Verhulst模型。得到其GM(1,1)模型的参数列
有负值,将负值去掉后得到用来进行灰色预测的原始数据序列为:X(Pi*)= (177 702, 217 890, 246 190, 263 813, 275 243, 283 458, 288 928, 299 738, 310 816)。根据X(Pi*),建立GM(1,1)模型、微分Verhulst模型以及差分Verhulst模型。得到其GM(1,1)模型的参数列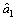 、微分Verhulst模型的参数列
、微分Verhulst模型的参数列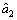 以及差分Verhulst模型的参数列
以及差分Verhulst模型的参数列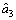 ,分别为:
,分别为: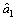 =(0.042 8, 221 543)T;
=(0.042 8, 221 543)T;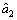 =(-0.011 9, 0.000 6)T;
=(-0.011 9, 0.000 6)T;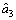 =(-0.011 7, -0.000 6)T。
=(-0.011 7, -0.000 6)T。
根据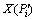 ,建立GM(1,1)模型、微分Verhulst模型以及差分Verhulst模型。得到其GM(1,1)模型的参数列
,建立GM(1,1)模型、微分Verhulst模型以及差分Verhulst模型。得到其GM(1,1)模型的参数列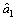 、微分Verhulst模型的参数列
、微分Verhulst模型的参数列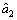 以及差分Verhulst模型的参数列
以及差分Verhulst模型的参数列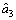 分别为
分别为
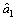 =(-0.022 2, 17.636 9)T;
=(-0.022 2, 17.636 9)T;
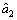 =(-0.470 1, -0.000 001 515)T;
=(-0.470 1, -0.000 001 515)T;
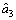 =(-0.475 7 -0.000 001 533)T
=(-0.475 7 -0.000 001 533)T
将参数列代入各自模型后求解得到各模型对于各测点的理论预测值,并进行误差比较及精度检验,结果如表4所示。
表4 各模型误差检验结果
Table 4 Error test results of each model
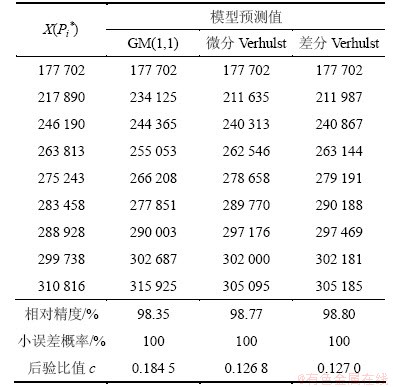
由表4可知:对于基于X(Pi’)的预测模型,差分Verhulst模型误差最小,精度也最高,因此,用差分Verhulst模型来生成能源需求的规律。得到基于X(Pi’)的差分Verhulst预测模型为
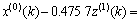

求解差分Verhulst预测模型,得到时间响应序列为

由于在整个数据序列中,第1个数据与第2个数据被排除在外,因此,实际上时间响应序列为
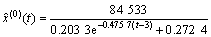
式中:t=1, 2, 3, …。
根据P序列,利用最小二乘法进行拟合得到线性拟合公式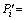 -0.000 4+0.008 9i,求得i=112.36
-0.000 4+0.008 9i,求得i=112.36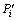 +0.04。此处i即为t,而r为历年能源需求影响因素灰色效果测度向量靶心距即
+0.04。此处i即为t,而r为历年能源需求影响因素灰色效果测度向量靶心距即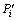 ,得到t=112.36r+0.04,代入上式得到能源需求量f(r)与影响因素灰色效果测度向量的靶心距r的规律公式为
,得到t=112.36r+0.04,代入上式得到能源需求量f(r)与影响因素灰色效果测度向量的靶心距r的规律公式为
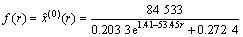 (18)
(18)
2.4 结果验证
2000—2010年能源需求影响因素灰色效果测度向量靶心距序列r为
r=(0.026 8, 0.025 0, 0.025 1, 0.026 7, 0.034 0, 0.040 1, 0.049 0, 0.066 0, 0.083 8, 0.092 6, 0.114 1)
2000—2010年能源需求量序列为
X(r)=(145 531, 150 406, 159 431, 183 792, 213 456, 235 997, 258 676, 280 508, 29 1448, 306 647, 324 938)。
将r序列代入式(18),得到相应的规律公式为
f(r)=(179 405, 172 074, 172 483, 179 001, 207 349, 228 440, 253 791, 284 758, 299 926, 303 746, 308 211)。
对X(r)与f(r)进行误差检验,得到其平均相对误差为6.09%,最小相对误差为0.946%。因此,采用式(18)分析2000—2015年的能源需求量规律时,结果比较可靠,可作为2000—2015年间我国能源需求规律表达式。运用这个表达式预测2011—2015年的能源需求量E=(347 613, 359 976, 374 807, 386 066,400 021)。
3 结论与建议
1) 利用改进灰靶决策理论与非等距预测模型对我国能源需求的规律进行分析,可以从内在本质上揭示能源需求量与主要影响因素的关系,而且可以通过各因素的指标值对能源需求量进行分析与预测。虽然很多理论模型都能通过分析历年的能源需求量的发展趋势而对能源需求量进行预测,但是通过能源需求的影响因素指标值的变化作为依据的能源需求量预测更加科学,且能将能源需求影响因素对能源需求量的影响加以量化分析。
2) 利用改进灰靶决策理论与非等距预测模型对我国能源需求的规律进行分析,能源需求各影响指标的灰色上限效果值与灰色下限效果值的准确确定与选择是关键。在改进灰靶决策分析时,权重确定的方式有很多种,本研究采用灰色关联度作为参照确定权重仅仅是一种参考,在相似研究中,可选取切实可靠的权重确定方式。在将非等距的预测模型转化为等距的预测模型时,对于因变量值X(Pi’)生成采用的是线性插值法,但拉格朗日法等可能会生成更加理想的X(Pi’),在进行类似研究时可以进行对比分析。
3) 利用改进灰靶决策理论与非等距预测模型对我国能源需求的规律进行分析,得到的规律比较可靠,可以在相似研究中进行应用。
4) 在实际应用时,应当注意改进灰靶决策的靶心距计算的方式和意义与传统的灰靶决策的靶心距计算方式和意义的差异。
参考文献:
[1] Akay D, Atak M. Grey prediction with rolling mechanism for electricity demand forecasting of Turkey[J]. Energy, 2007, 32(9): 1670-1675.
[2] 王珏, 鲍勤. 基于小波神经网络的中国能源需求预测模型[J]. 系统科学与数学, 2009, 29(11): 1542-1551.
WANG Jue, BAO Qin. Energy demand forecasting model in China based on wavelet-neural network[J]. Journal of System Science and Mathematical Sciences, 2009, 29(11): 1542-1551.
[3] Ceylan H, Ozturk H K. Estimating energy demand of Turkey based on economic indicators using genetic algorithm approach[J]. Energy Convers Manage, 2004, 45(15/16): 2525-2537.
[4] 邓志茹. 我国能源供求预测研究[D]. 哈尔滨: 哈尔滨工程大学经济管理学院, 2011: 35-45.
DENG Zhiru. Research on the forecast of energy supplying and demanding in China[D]. Harbin: Harbin Engineering University. School of Economics and Management, 2011: 35-45.
[5] CHEN Shiwei, LI Zhuguo, XU Qisheng. Grey target theory based equipment condition monitoring and wear mode recognition[J]. Wear, 2006, 260: 438-449.
[6] 王正新, 党耀国, 杨虎. 改进的多目标灰靶决策方法[J]. 系统工程与电子技术, 2009, 31(11): 2634-2636.
WANG Zhengxin, DANG Yaoguo, YANG Hu. Improvements on decision method of grey target[J]. Systems Engineering and Electronics, 2009, 31(11): 2634-2636.
[7] DANG Luo, XIA Wang. The multi-attribute grey target decision method for attribute value within three-parameter interval grey number[J]. Applied Mathematical Modelling, 2012, 37: 1957-1963.
[8] 郭丽萍, 孙伟, 郑克仁, 等. 非等时距GM(1,1)直接模型及其在材料试验数据处理中的应用[J]. 东南大学学报(自然科学版), 2004, 34(6): 39-41.
GUO Liping, SUN Wei, ZHENG Keren, et al. Non-equal interval GM(1,1) direct model and its application in processing of materials experimental data[J]. Journal of Southeast University (Natural Science Edition), 2004, 34(6): 39-41.
[9] Boche H, M nich U. Convergence behavior of non-equidistant sampling series[J]. Signal Processing, 2010, 90: 145-156.
nich U. Convergence behavior of non-equidistant sampling series[J]. Signal Processing, 2010, 90: 145-156.
[10] 张宏, 李仲学. 煤炭需求影响因素及情景分析[J]. 煤炭学报, 2007, 32(5): 557-560.
ZHANG Hong, LI Zhongxue. Affecting factors and projected scenarios for coal demand in China[J]. Journal of China Coal Society, 2007, 32(5): 557-560.
[11] YU Shiwei, ZHU Kejun, ZHANG Xian. Energy demand projection of China using a path-coefficient analysis and PSO-GA approach[J]. Energy Conversion and Management, 2012, 53(1): 142-153.
[12] Kayacan E, Ulutas B, Kaynak O. Grey system theory-based models in time series prediction[J]. Expert Systems with Applications, 2010, 37(2): 1784-1789.
[13] WANG Yuhong, DANG Yaoguo, LI Yueqing, et al. An approach to increase prediction precision of GM(1,1) model based on optimization of the initial condition[J]. Expert Systems with Applications, 2010, 37(8): 5640-5644.
[14] 刘思峰, 郭天榜, 党耀国, 等. 灰色系统理论及其应用[M]. 北京: 科学出版社, 1999: 80-144.
LIU Sifeng, GUO Tianbang, DANG Yaoguo, et al. The grey system theory and its application[M]. Beijing: Science Press, 1999: 80-144.
[15] WANG Zhengxin, DANG Yaoguo, LIU Sifeng. Unbiased grey Verhulst model and its application[J]. Systems Engineering (Theory & Practice), 2009, 29(10): 138-144.
[16] 单珂. 高速公路路基沉降影响因素的研究[J]. 内蒙古民族大学学报(自然科学版), 2012, 27(1): 37-40.
SHAN Ke. Highway embankment settlement influencing factors[J]. Journal of Inner Mongolia University for Nationalities (Natural Science Edition), 2012, 27(1): 37-40.
[17] XU Jin, TAN Tao, TU Mao, et al. Improvement of grey models by least squares[J]. Expert Systems with Applications, 2011, 38(11): 13961-13966.
[18] 刘洋, 陈传波, 王国霞, 等. 基于灰色系统理论的湖南省电力需求分析与预测[J]. 湖南大学学报(自然科学版), 2005, 32(5): 71-74.
LIU Yang, CHEN Chuanbo, WANG Guoxia, et al. Analysis and forecast of Hunan Province’s demand for electric power based on fuzzy theory[J]. Journal of Hunan University (Natural Sciences), 2005, 32(5): 71-74.
[19] 于凤玲, 陈建宏. 基于灰色关联与优势分析的能源消费与工业环境污染的实证研究[J]. 环境污染与防治, 2012, 34(11): 93-97.
YU Fengling, CHEN Jianhong. Empirical research of the relationship between energy consumption and industrial environment pollution based on grey relevance superior method[J]. Environmental Pollution & Control, 2012, 34(11): 93-97.
(编辑 陈灿华)
收稿日期:2013-09-12;修回日期:2013-11-25
基金项目:国家自然科学基金资助项目(51374242)
通信作者:于凤玲(1977-),女,湖南新宁人,博士,讲师,从事经济与金融研究;电话:1399078595;E-mail: flingyu77@163.com