Numerical investigation of laminar heat transfer and nanofluid flow between two porous horizontal concentric cylinders
来源期刊:中南大学学报(英文版)2019年第7期
论文作者:Mehdi MIRZAEYAN Davood TOGHRAIE
文章页码:1976 - 1999
Key words:porous horizontal concentric cylinders; nanofluid flow; permeability; heat transfer
Abstract: In this study, the laminar heat transfer and nanofluid flow between two porous horizontal concentric cylinders was investigated. The problem is investigated in two different geometries and the Re=10, 25, 50, 75, 100 and volume fraction 0, 0.2%, 0.5%, 2% and 5% that related to copper nanoparticles, and porous medium porosity of 0.5 and 0.9. Compared to the first geometry, the convective coefficient in the second geometry increases by 8.3%, 7% and 5.5% at Reynolds numbers of 100, 75 and 50, respectively. Comparison of the outlet temperatures for two heat fluxes of 300 and 1200 W/m2 indicates a 2.5% temperature growth by a fourfold increase in the heat fluxes. Also, the higher Nusselt number is associated with the second geometry occurring at porosities of 0.9 and 0.5, respectively. In both geometries, the Nusselt number values at the porosity of 0.9 are higher, which is due to the increased nanofluid convection at higher porosities. The velocity of the nanofluid experiences a two-fold increase at the outlet compared to its inlet velocity in the first geometry and for both porosities. Similarly, a three-fold increase was achieved in the second geometry and for both porosities.
Cite this article as: Mehdi MIRZAEYAN, Davood TOGHRAIE. Numerical investigation of laminar heat transfer and nanofluid flow between two porous horizontal concentric cylinders [J]. Journal of Central South University, 2019, 26(7): 1976-1999. DOI: https://doi.org/10.1007/s11771-019-4146-z.

J. Cent. South Univ. (2019) 26: 1976-1999
DOI: https://doi.org/10.1007/s11771-019-4146-z
Mehdi MIRZAEYAN, Davood TOGHRAIE
Department of Mechanical Engineering, Khomeinishahr Branch, Islamic Azad University,Khomeinishahr, Iran
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019
Abstract: In this study, the laminar heat transfer and nanofluid flow between two porous horizontal concentric cylinders was investigated. The problem is investigated in two different geometries and the Re=10, 25, 50, 75, 100 and volume fraction 0, 0.2%, 0.5%, 2% and 5% that related to copper nanoparticles, and porous medium porosity of 0.5 and 0.9. Compared to the first geometry, the convective coefficient in the second geometry increases by 8.3%, 7% and 5.5% at Reynolds numbers of 100, 75 and 50, respectively. Comparison of the outlet temperatures for two heat fluxes of 300 and 1200 W/m2 indicates a 2.5% temperature growth by a fourfold increase in the heat fluxes. Also, the higher Nusselt number is associated with the second geometry occurring at porosities of 0.9 and 0.5, respectively. In both geometries, the Nusselt number values at the porosity of 0.9 are higher, which is due to the increased nanofluid convection at higher porosities. The velocity of the nanofluid experiences a two-fold increase at the outlet compared to its inlet velocity in the first geometry and for both porosities. Similarly, a three-fold increase was achieved in the second geometry and for both porosities.
Key words: porous horizontal concentric cylinders; nanofluid flow; permeability; heat transfer
Cite this article as: Mehdi MIRZAEYAN, Davood TOGHRAIE. Numerical investigation of laminar heat transfer and nanofluid flow between two porous horizontal concentric cylinders [J]. Journal of Central South University, 2019, 26(7): 1976-1999. DOI: https://doi.org/10.1007/s11771-019-4146-z.
1 Introduction
Nanofluids are suspensions of nanoparticles in convectional base fluids. These mixtures have enhanced thermal properties [1-16]. The study of heat transfer in porous media has many important applications in many technologies. Porous media increase the contact surface area between liquid and solid surface and nanoparticles enhance the thermal conductivity. Therefore, using porous media and nanofluid can augment the efficiency of thermal systems. Some researchers have carried out studies to observe the behavior of the flow and heat transfer of the nanofluids in porous media.
MAGHREBI et al [17] investigated forced convection heat transfer of nanofluids in a porous channel. They observed that as the Schmidt number is increased, the local Nusselt number decreased. SHEIKHOLESLAMI et al [18] investigated nanofluid flow in a semi-porous channel in the presence of uniform magnetic field. They found that that the velocity boundary layer thickness decreases with increasing Reynolds number and nanoparticle volume friction, and it increases while Hartmann number increases. SALEH [19] studied laminar free convection of nanofluid flow in horizontal porous annulus. They found that as volume fraction of nanoparticles increases, difference for average Nusselt number becomes larger due to the increase of domination of convection mode of heat transfer. MAHDI et al [20] reviewed improvement of convection heat transfer by using porous media and nanofluid. The effects of several parameters in porous media geometry and nanofluid properties, thermal boundary conditions, and types of fluids were investigated. ARMAGHANI et al [21] analyzed nanofluid forced convection in a porous channel. Their results showed that the heat flux at the wall absorbed by the fluid phase is increased by increasing the Nield number. PAL et al [22] investigated mixed convection stagnation-point flow of nanofluids in a porous medium with internal heat generation/absorption. SHEIKHOLESLAMI et al [23] investigated nanofluid flow and heat transfer over a stretching porous cylinder. Their results show that skin friction coefficient increases with increase of Reynolds number but it decreases with increase of nanoparticle volume fraction. ZEHFOROOSH et al [24] investigated the Brownian motion of CuO-water nanofluid in a porous cavity with internal heat generation. Their results show that Brownian term reduces nanofluid velocity and makes smoother streamlines, and increasing the thermal conductivity leads to cooling of porous material and achieving more Nusselt. NOJOOMIZADEH et al [25] investigated the effects of porosity and permeability on fluid flow and heat transfer of nanofluid in a microchannel filled with a porous medium. They concluded that a decrease in porosity has greater impact on Nusselt numbers; hence for high Reynolds numbers and low porosity and Darcy, the amount of increase in the local Nusselt number would be greater. TU et al [26] studied thermal characteristic of a tube fitted with porous media inserts in the single phase flow. They found that the best performance evaluation criterion (PEC) value is 1.26-1.71. KASAEIAN et al [27] reviewed nanofluid flow and heat transfer in porous media. They found that Tiwari and Das, and Buongiorno models were the most popular models used to simulate the nanofluid flow in porous media.MOJUMDER et al [28] studied mixed convection heat transfer in a porous L-shaped cavity. They concluded that higher Darcy and Grashof numbers result in lower average fluid temperatures at low Reynolds number, whereas low Grashof and Darcy numbers are desirable when the Reynolds number is high to lower the average fluid temperature inside the cavity.
In this study, the laminar heat transfer and nanofluid flow between two porous horizontal concentric cylinders was investigated. The problem is investigated in two different geometries and the Re=10, 25, 50, 75,100 and volume fraction 0, 0.2%, 0.5%, 2% and 5% that were related to copper nanoparticles, and porous medium porosity of 0.5, 0.9.
2 Problem statement
2.1 Governing equations for an incompressible, steady-state nanofluid flow in a porous medium
Continuity equation [29]:
 (1)
(1)
Momentum equation [29]:
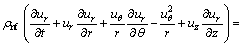
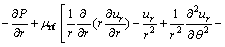
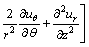 (2)
(2)
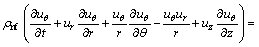

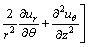 (3)
(3)
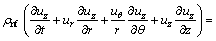
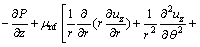
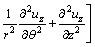 (4)
(4)
Energy equation:

 (5)
(5)
where E is the total energy, ρ is the density, ε is the porosity, h is the enthalpy, J is the permeation flux, subscripts nf and s represent the nanofluid and solid phases, respectively, keff is the effective thermal conductivity, and τ is the stress tensor. Also,
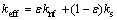 (6)
(6)
 (7)
(7)
where I denotes the identity tensor, and the second term on the right side of the equation relates to the effects of volume expansion.
2.2 Nanofluid equations
Thermal conductivity [29],
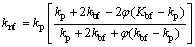 (8)
(8)
Specific heat [29],
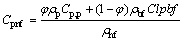 (9)
(9)
Density [29],
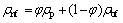 (10)
(10)
Dynamic viscosity [29],
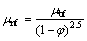 (11)
(11)
Coefficient of thermal expansion [29],
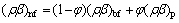 (12)
(12)
Thermophysical properties of the base fluid and the copper nanoparticles are given in Table 1.
Permeability coefficient:
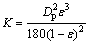 (13)
(13)
2.3 Problem assumptions
The following assumption were made in this investigation:
1. Laminar flow.
2. Incompressible flow.
3. Newtonian fluid.
4. Negligible viscous dissipation.
5. Homogenous porous medium fully saturated by and in thermal equilibrium with the nanofluid.
6. Negligible nanoparticles size compared to the porous solid’s pores.
2.4 Geometry descriptions
Two concentric cylinders form the geometry. The inner cylinder is solid and the porous grid is implemented between the two cylinders on the inner and outer walls. The sector-shaped porous medium on the cylinder wall covers a larger cross-sectional area of the geometry as the grid grows radially. The cross-sectional areas for the first and second geometries are depicted in Figure 1. The two solid porous grids on the cylinder walls in the second geometry approach one another in the radial direction, roughly occluding the fluid passage cross-section between the two solid grids. The porous media in both figures are marked by shaded areas. Except for the 30° angles, all dimensions in both figures are in millimeter. Both geometries are 1 m long along the z direction. Constant heat fluxes of 300 W are applied as the boundary condition on both cylinder walls. This boundary condition remains constant in all cases, since the objective is to investigate parametric changes such as fluid inlet velocity, the porosity of the porous solid, the positioning of the porous medium inside the pipe, and volumetric fraction of the nanofluid. Therefore, the effects of these parameters on the problem are compared at a constant heat flux boundary condition. Considering the symmetry, the problem is solved for one-fourth of the geometry so that the number of generated cells and the solution runtime are reduced, and the meshing process is facilitated. Since the permeability of the nanofluid is considered similar along the three principal axes, the viscous and inertial resistances are also assumed equal along all directions for this medium.
2.5 Grid independency
As mentioned earlier, one-fourth of the geometry was meshed. Considering the different grids selected for each geometry, the velocity profiles and the solutions for each grid were plotted. The velocity profile for the second geometry is presented in Figure 2. According to the percentage of difference between the velocity profiles in each grid in consecutive grids, it can be observed that by increasing cell number to more than 278775, the obtained numerical results do not change; therefore, in order to reduce the time of calculations, this cell number has been used for all studied conditions.
Table 1 Thermophysical properties of base fluid (water) and copper nanoparticles [29]


Figure 1 Cross-sectional area of geometries (Unit: mm):
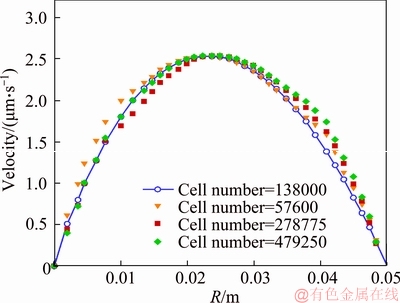
Figure 2 Velocity profiles in different grids (second geometry)
2.6 Validation
The results were validated with the work of ZHAO et al [30] (see Figure 3). Hence, the present study also plotted the diagram of Nusselt number variations on the inner wall of the cylinder for the second geometry at the same Reynolds number and volumetric fraction and a porosity of 0.5. The diagrams were then compared and a mean difference of 6% was obtained that can be attributed to the difference in geometry as well as the presence of a porous medium in the present problem.
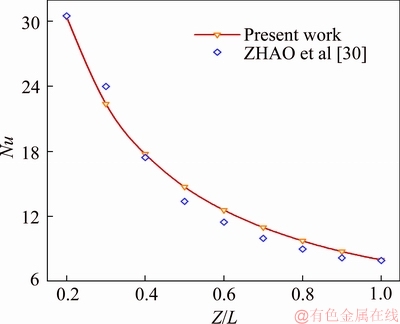
Figure 3 Problem validation using results reported by ZHAO et al [30]
3 Results and discussion
3.1 Convective heat transfer coefficient
The local temperature of the wall is the only parameter contributing to the convective heat transfer rate in case a constant heat flux boundary condition is applied and a constant inlet temperature is assumed for the nanofluid. The variation of convective heat transfer coefficient at different volumetric fractions and Reynolds numbers in the first and second geometries for porosity of 0.5 is shown in Figure 4. According to the diagrams, the convective heat transfer coefficient values are higher in the second geometry compared to the first one, which is an advantage more evidently seen at higher Reynolds numbers. These values are close in the two geometries at low Reynolds numbers. Compared to the first geometry, the convective coefficient in the second geometry increases by 8.3%, 7% and 5.5% at Reynolds numbers of 100, 75, and 50, respectively. Convective heat transfer coefficient in convection mechanism is a function of fluid movements, type, and geometry. Given a similar fluid type, the other two parameters, i.e., fluid geometry and movement influence the variations in the convective coefficient. In the second geometry, the fluid velocity increases due to the reduction in the equivalent diameter of the pipe cross-section, consequently increasing the convective coefficient. The higher variability of the convective coefficient at higher Reynolds numbers is due to its dependency on the fluid velocity. The convective coefficient decreases at higher volumetric fractions, where the static mechanism of the nanofluid is dominant and its velocity is reduced due to the presence of nanoparticles. The decrease in this coefficient in both geometries ranged from 13% to 16% for Reynolds numbers ranging from 50 to 100. Moreover, at Reynolds numbers of 25 and 10, the reductions were 20% and 25%. The convective coefficient sees a greater reduction at the Reynolds number of 10 due to decreased velocity.
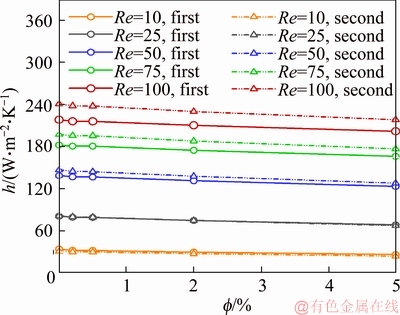
Figure 4 Variation of convective heat transfer coefficient with respect to volumetric fraction on wall of inner cylinder in first and second geometries for different Reynolds numbers and a porosity of 0.5
Variation of convective coefficient with respect to different volumetric fractions and Reynolds numbers in the first and second geometries for porosity of 0.9 is demonstrated in Figure 5. As shown, higher convective coefficient values are achieved in the second geometry compared to the first one. The convective coefficients of the first geometry at Reynolds numbers of 100, 75, 50, and 25 increased by 11.3%, 10%, 8% and 4.5% compared to the second geometry, respectively. The diagrams of convective coefficient for both geometries overlap at a Reynolds number of 10. Due to the high nanofluid velocity, the difference between the connective coefficient values is larger at higher Reynolds numbers. Increasing porosity and decreasing the equivalent diameter in the second geometry lead to increased penetration of the nanofluid into the porous medium and, consequently, to an increased heat transfer rate resulting from an increase in the absorbed heat from the medium. In the first geometry, the larger portion of the nanofluid passes through the free region, i.e., the non-porous medium, and a smaller portion penetrates into the porous medium. Comparison between the diagrams provided in this figure with those of Figure 4 reveals that, compared to the porosity of 0.5, a 3% increase is observed in the convective coefficient values at the porosity of 0.9, which can be attributed to the increased permeability of the porous medium. The convective coefficient increases by 5% and 10% at Reynolds numbers of 25 and 10 by changing the porosity from 0.5 to 0.9, respectively. At higher volumetric fractions and for different Reynolds numbers, the convective coefficient experiences a decrease ranging from 4.5% to 6% and 2.5% to 5% in the first and second geometries, respectively. This decrease is 11% at a Reynolds number of 10.
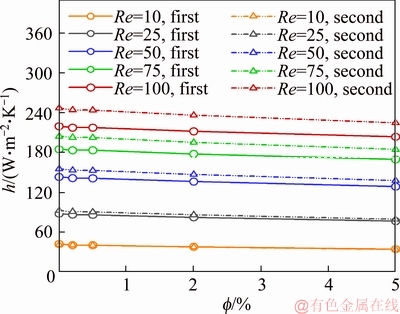
Figure 5 Variation of convective heat transfer coefficient with respect to volumetric fraction on wall of inner cylinder in first and second geometries for different Reynolds numbers and a porosity of 0.9
Variation of convective coefficient at different volumetric fractions and Reynolds numbers in the first and second geometries for porosities of 0.5 and 0.9 is shown in Figure 6. The diagrams of convective coefficient at both porosities overlap. At lower Reynolds numbers, the convective coefficient is higher for the porosity of 0.9 compared to that of 0.5. These increases are 1%, 3%, 9% and 19% at Reynolds numbers of 75, 50, 25, and 10. Compared to the porosity of 0.5, a larger portion of the nanofluid passes through the porous medium at the porosity of 0.9, leading to a greater heat transfer rate. At lower Reynolds numbers, a greater heat transfer rate is achieved as the porosity conditions approach towards higher values and, ultimately, towards a non-porous medium. At lower Reynolds numbers and higher porosities, the nanofluid penetrates into the porous medium to a greater degree, as it can more easily penetrate into the porous medium at lower velocities, which subsequently increases the heat transfer rate by absorbing more heat from the porous solids.

Figure 6 Convective heat transfer coefficient with respect to volumetric fraction on wall of inner cylinder at different volumetric fractions and porosities of 0.5 and 0.9 in first geometry
Variation of convective coefficient at different volumetric fractions and Reynolds numbers for porosities of 0.5 and 0.9 is shown in Figure 7 for the first geometry. Similar to Figure 6, the convective coefficient assumes larger values at the porosity of 0.9 compared to that of 0.5, which is due to the greater volume of nanofluid passing through the porous medium and increasing the heat transfer rate. By increasing the porosity from 0.5 to 0.9, the convective heat transfer increases by 2.5%, 6.5%, 13% and 25% at Reynolds numbers of 100, 75, 25, and 10, respectively. Lower Reynolds numbers correspond to lower nanofluid velocities. As the porosity of the porous medium increases, the nanofluid penetrates into the medium to a greater degree, increasing the convective coefficient and the heat transfer rate. For a given geometry, the porosity of the porous medium plays a less significant role in increasing or decreasing the heat transfer rate and convective coefficient.
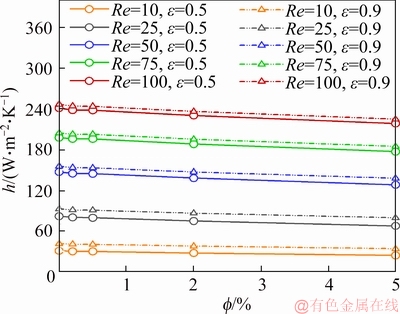
Figure 7 Variation of convective heat transfer coefficient with respect to volumetric fraction on wall of inner cylinder at different volumetric fractions and porosities of 0.5 and 0.9 in second geometry
3.2 Assessment of heat transfer at a Reynolds number of 100 and different heat fluxes
The problem was studied and analyzed for a heat flux of 300 W/m2 and the results were reported. Considering the variables involved in the problem and their effects on the heat transfer rate, the heat flux applied on the wall of the inner and outer cylinders was considered as another variable. The effects of heat flux values of 600 and 1200 W/m2 on the heat transfer rate at a Reynolds number of 100 and volumetric fractions of 0%, 0.2% and 0.5% were investigated. Moreover, the variations of the temperature along the axis as well as the Nusselt number over the surface of the inner cylinder with respect to the volumetric fraction of nanoparticles were presented in diagrams. The results were compared for the first and second geometries at porosities of 0.5 and 0.9. The diagrams of temperature at the pipe outlet with respect to the volumetric fraction of nanoparticles were plotted for heat fluxes of 300, 600, and 1200 W/m2 and porosities of 0.5 and 0.9 in Figures 8 and 9 for the first and second geometries.
The outlet temperature at a heat flux of 1200 W/m2 is shown in Figure 8. As shown, the higher outlet temperatures correspond to porosities of 0.5 and 0.9 in the first geometry, suggesting the better heat transfer condition of the first geometry compared with the second one. In addition, the outlet temperature increases by increasing the volumetric fraction of nanoparticles, so that in both geometries and porosities, the outlet temperature increases by 0.1% by increasing the volumetric fraction from 0 to 0.5%. Compared to the second geometry, the temperature grows by 0.15% for both porosities of 0.5 and 0.9 in the first geometry. In addition, for each geometry, comparison of the outlet temperature indicates a growth of roughly 0.03% by increasing the porosity from 0.5 to 0.9. These comparisons suggest that changing the geometry and increasing the volumetric fraction have the highest influence on the heat transfer rate, respectively. The first geometry provides a larger free space in its porous solids across the pipe cross-section, through which a larger volume of the nanofluid can pass to facilitate the heat transfer process by absorbing a larger amount of heat from the porous blocks and pipe wall. In these conditions, the nanofluid absorbs more heat from the surface of the porous medium due to the reduced penetrability of the nanofluid. However, at higher porosities, the increased penetration of the nanofluid into the porous medium decreases the nanofluid velocity and, consequently, the heat transfer rate. The diagrams of outlet temperature at heat fluxes of 300 and 600 W/m2 are plotted and compared in Figure 9. Similar to Figure 8, the first and second geometries were considered in this comparison at porosities of 0.5 and 0.9 and, in addition, the outlet temperature was investigated with respect to the volumetric fraction of nanoparticles. As the diagrams suggest, a two-fold increase in the heat flux results in a 0.7% growth in the outlet temperature of both geometries and porosities. Comparison between the outlet temperatures in Figures 8 and 9 for heat fluxes of 600 and 1200 W/m2 shows a 2% growth in both geometries and porosities as the heat fluxes experience a two-fold increase. Furthermore, comparison of the outlet temperatures for two heat fluxes of 300 and 1200 W/m2 indicates a 2.5% temperature growth by a four-fold increase in the heat fluxes. At higher heat fluxes, the nanofluid temperature experiences a faster increase as it approaches the surface temperature. A decreased temperature difference between the nanofluid and the pipe wall reduces the exchanged heat between the surface and the nanofluid and, therefore, prevents the proportional increase of the nanofluid temperature at the outlet to the increased heat flux.

Figure 8 Outlet temperature diagrams for first and second geometries at porosities of 0.5 and 0.9 and a heat flux of 1200 W/m2
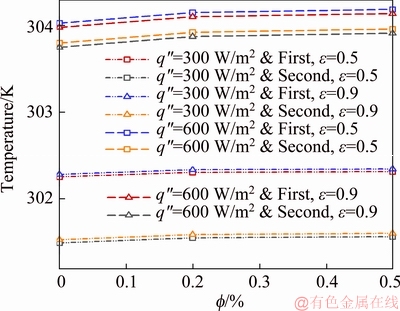
Figure 9 Outlet temperature diagrams for first and second geometries at porosities of 0.5 and 0.9 and heat fluxes of 300 and 600 W/m2
3.3 Effect of variations of heat flux on mean Nusselt number at a Reynolds number of 10
Variation of the Nusselt number with respect to volumetric fraction of nanoparticles for both geometries and porosities at a heat flux of 600 W/m2 is demonstrated in Figure 10. Based on the relation of convective heat transfer coefficient and assuming a constant inlet temperature, the temperature changes of the cylinder walls are dependent on changes in the heat flux. At different heat fluxes and given roughly similar geometry, porosity, and volumetric fraction conditions, increasing the temperature and heat flux results in almost similar convective heat transfer coefficient values with insignificant differences. Considering that at constant geometry, porosity, and volumetric fraction conditions the convective coefficient remains unchanged as the heat flux changes, it may be concluded that the Nusselt number is also independent of the heat flux. As shown, the diagrams of Nusselt number at different heat fluxes for both geometries and porosities almost overlap. The dependency of the Nusselt number on the geometry and porosity is demonstrated in Figure 10. As shown, the higher Nusselt number is associated with the second geometry occurring at porosities of 0.9 and 0.5, respectively. In both geometries, the Nusselt number values at the porosity of 0.9 are higher, which is due to the increased nanofluid convection at higher porosities. Variations of the Nusselt number in both geometries and porosities are slight, so that in the first geometry, a 0.5% growth is achieved by changing the porosity from 0.9 to 0.5. This growth is 2.3% in the second geometry. Comparison of variations in the Nusselt number between the two geometries at the same porosity reveals that a 9% increase is obtained in the Nusselt number in the second geometry compared to the first geometry at a porosity of 0.5. This increase reaches up to 11% at a porosity of 0.9, indicating the dominant effect of convection over conduction mechanism due to the increased nanofluid velocity in the second geometry filled with the porous solid.
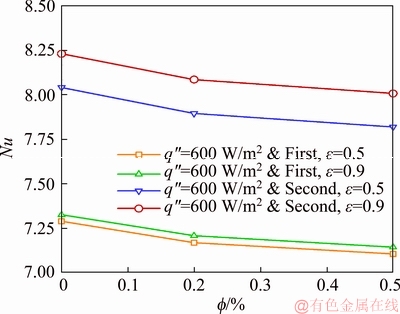
Figure 10 Variation of Nusselt number for first and second geometries at porosities of 0.5 and 0.9 and a heat flux of 600 W/m2
3.4 Temperature, velocity, and pressure contours
The temperature contours for the first and second geometries at porosities of 0.5 and 0.9, volumetric fractions of 0 and 2%, and Reynolds numbers of 10, 50, and 100 are shown in Figures 11-14. Compared to the inlet temperature, the nanofluid temperature at the outlet increases by 10%, 2.5% and 1.5% at Reynolds numbers of 10, 50, and 100 in both geometries and porosities, respectively. By increasing the volumetric fraction from 0 to 2%, the outlet temperature at Reynolds numbers of 10, 50, and 100 increases by 1.5%, 0.3%, and 0.2%, respectively. The results demonstrate that the Reynolds number has a higher effect on the nanofluid temperature at the outlet compared to such factors as geometry, porosity, and volumetric fraction. This effect is more evident at low Reynolds numbers, where the nanofluid further penetrates the porous medium and transfers heat from the pipe surface to the porous medium through conduction. This is confirmed through the regular pattern and uniform distribution of heat shown in temperature contours at a Reynolds number of 10. At Reynolds numbers of 50 and 100, the nanofluid penetrates the porous medium to a lower extent, absorbing and transferring less amount of heat from the surface of the pipe wall. In this condition, heat is not diffused in regular and distinct layers, and the temperature layers experience a larger growth along the pipe axis within the non-porous medium. The velocity contours for the first and second geometries at porosities of 0.5 and 0.9, volumetric fractions of 0 and 2%, and Reynolds numbers of 10, 50, and 100 are shown in Figures 15-18. As shown, the velocity of the nanofluid experiences a two-fold increase at the outlet compared to its inlet velocity in the first geometry and for both porosities. Similarly, a three-fold increase was achieved in the second geometry and for both porosities. The nanofluid velocity sees a greater increase in the second geometry due to the decrease in pipe cross-sectional area along the free space (non-porous medium). Compared to its inlet velocity, the nanofluid experiences a drastic decrease in its velocity at the outlet as it passes through the porous solids. In both geometries, this decrease in the outlet velocity is larger for the porosity of 0.9 compared to the porosity of 0.5. Considering that the velocity increases along the pipe axis, the heat is expected to be a function of velocity and propagated along the same direction. However, the diffusion of heat along all directions indicates the significant role of the porous medium. The porous medium diffuses heat along all direction through conduction and further mixing of the nanofluid flow.
The pressure contours for the first and second geometries at porosities of 0.5 and 0.9, volumetric fractions of 0 and 2%, and Reynolds numbers of 10, 50, and 100 are shown in Figures 19-21. Based on the Ergun relation [31] for the overall pressure drop in a laminar flow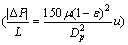 and considering the pressure contours, it can be observed that the pressure drop is directly proportional to the fluid velocity, such that the pressure drop experiences a 10- and 2-fold increase by reducing the Reynolds number from 100 to 10 and 50, respectively. The pressure drop increases by 5-fold by changing the Reynolds number from 50 to 10. By increasing the volumetric fraction, the overall pressure drop decreases at high volumetric fractions due to the decreased nanofluid velocity. By investigating the effect of geometry and porosity on pressure drop in these contours, it is revealed that the pressure drop is increased by 1.2 and 1.5 in the first and second geometries, respectively, by increasing the porosity from 0.5 to 0.9. Comparison of the pressure drops in the two geometries and porosities shows that the highest pressure drop is associated with the second geometry at a porosity of 0.5, while the lowest is associated with the first geometry at a porosity of 0.9. The pressure experiences a larger drop in the second geometry compared to the first one for both porosities, since a larger cross-sectional area of the pipe is filled with porous materials that resist the nanofluid flow and cause a pressure drop in the pipe. Comparison of the pressure drop in the nanofluid and porous materials suggests that in the first geometry and for porosities of 0.5 and 0.9, the pressure drop experiences a 15- and 1.2-fold increase with respect to the nanofluid. Compared to the nanofluid, the pressure in the porous material experiences a 3-fold drop at a porosity of 0.5. In the second geometry, the pressure drops in both regions are similar at a porosity of 0.9. Compared to the nanofluid, the highest increase in the pressure drop in the porous material occurs in the first geometry for the porosity of 0.5, the reason for which can be attributed to the larger free cross-sectional area of the pipe (with no porous medium) and the low porosity of the porous material, which in turn causes a reduced resistance against the nanofluid flow. In the second geometry and for a porosity of 0.9, the space through which the nanofluid passes is filled with the porous material and, therefore, a larger volume of the nanofluid passes through these porous medium, causing the pressure drop value to be equal in these two regions.
and considering the pressure contours, it can be observed that the pressure drop is directly proportional to the fluid velocity, such that the pressure drop experiences a 10- and 2-fold increase by reducing the Reynolds number from 100 to 10 and 50, respectively. The pressure drop increases by 5-fold by changing the Reynolds number from 50 to 10. By increasing the volumetric fraction, the overall pressure drop decreases at high volumetric fractions due to the decreased nanofluid velocity. By investigating the effect of geometry and porosity on pressure drop in these contours, it is revealed that the pressure drop is increased by 1.2 and 1.5 in the first and second geometries, respectively, by increasing the porosity from 0.5 to 0.9. Comparison of the pressure drops in the two geometries and porosities shows that the highest pressure drop is associated with the second geometry at a porosity of 0.5, while the lowest is associated with the first geometry at a porosity of 0.9. The pressure experiences a larger drop in the second geometry compared to the first one for both porosities, since a larger cross-sectional area of the pipe is filled with porous materials that resist the nanofluid flow and cause a pressure drop in the pipe. Comparison of the pressure drop in the nanofluid and porous materials suggests that in the first geometry and for porosities of 0.5 and 0.9, the pressure drop experiences a 15- and 1.2-fold increase with respect to the nanofluid. Compared to the nanofluid, the pressure in the porous material experiences a 3-fold drop at a porosity of 0.5. In the second geometry, the pressure drops in both regions are similar at a porosity of 0.9. Compared to the nanofluid, the highest increase in the pressure drop in the porous material occurs in the first geometry for the porosity of 0.5, the reason for which can be attributed to the larger free cross-sectional area of the pipe (with no porous medium) and the low porosity of the porous material, which in turn causes a reduced resistance against the nanofluid flow. In the second geometry and for a porosity of 0.9, the space through which the nanofluid passes is filled with the porous material and, therefore, a larger volume of the nanofluid passes through these porous medium, causing the pressure drop value to be equal in these two regions.
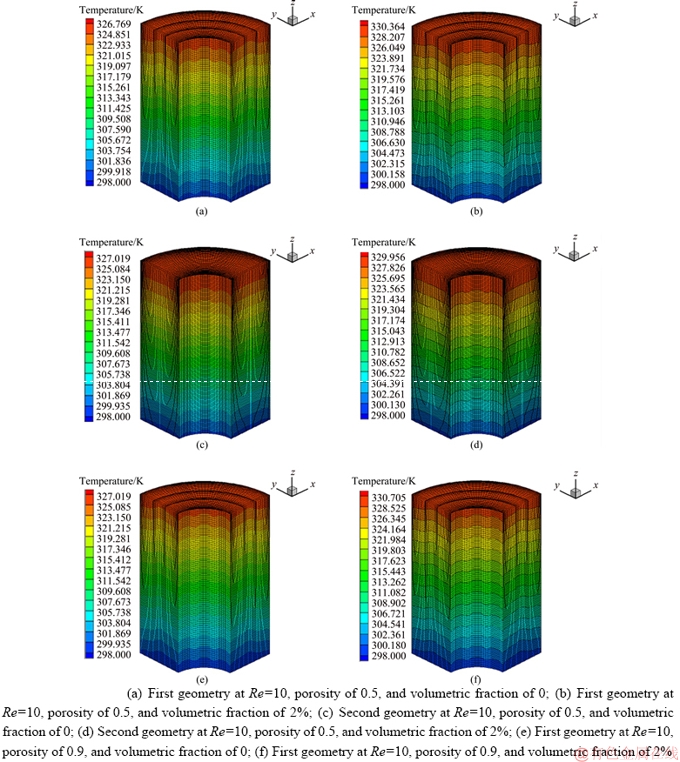
Figure 11 Temperature contour for first and second geometries at different Reynolds numbers, porosities and volumetric fractions:
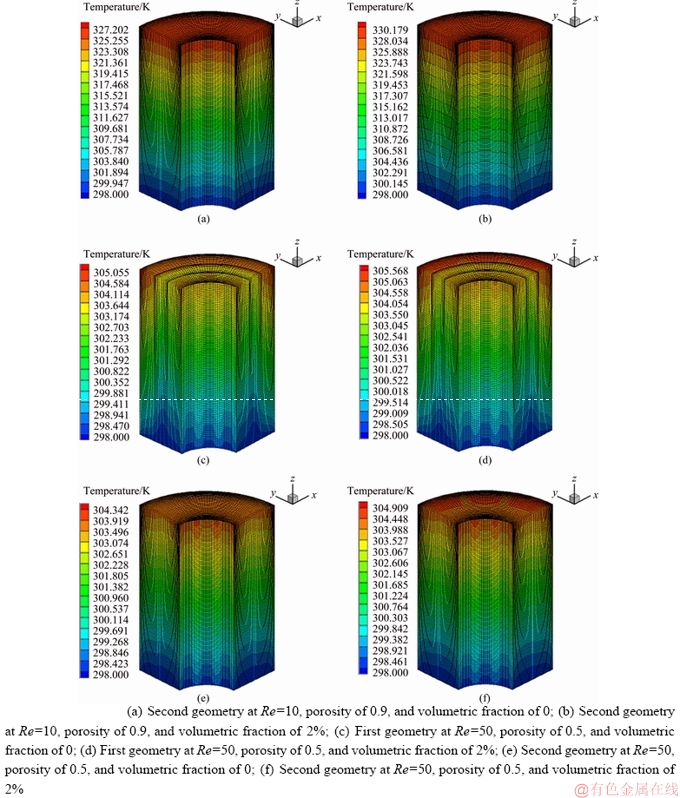
Figure 12 Temperature contour for first and second geometries at different Reynolds numbers, porosities and volumetric fractions:
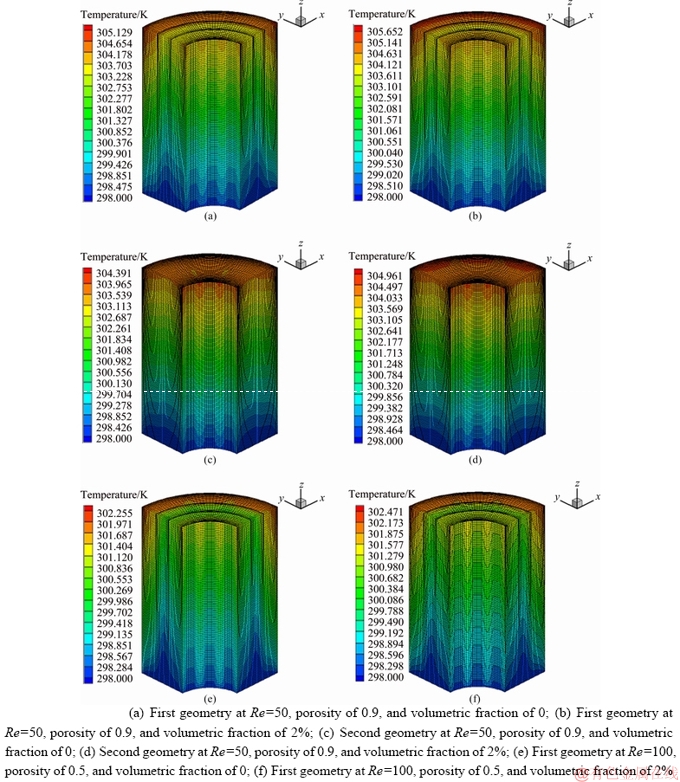
Figure 13 Temperature contour for first and second geometries at different Reynolds numbers, porosities and volumetric fractions:
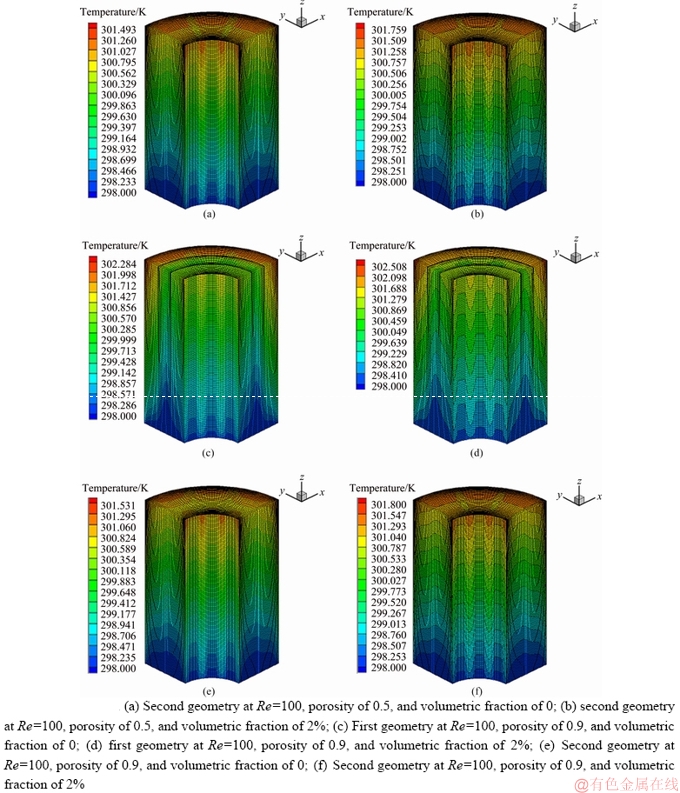
Figure 14 Temperature contour for first and second geometries at different Reynolds numbers, porosities and volumetric fractions:

Figure 15 Velocity contour for first and second geometries at different Reynolds numbers, porosities and volumetric fractions:

Figure 16 Velocity contour for first and second geometries at different Reynolds numbers, porosities and volumetric fractions:

Figure 17 Velocity contour for first and second geometries at different Reynolds numbers, porosities and volumetric fractions:
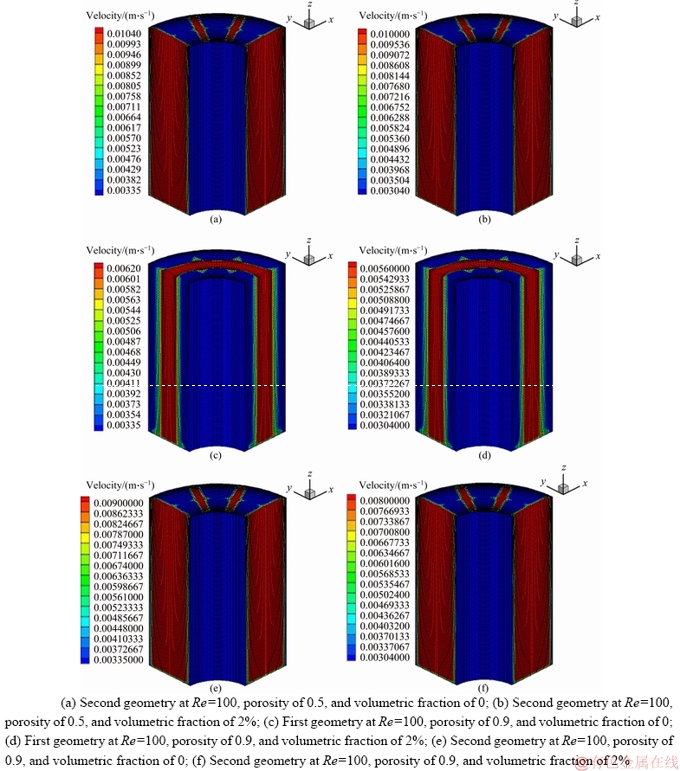
Figure 18 Velocity contour for first and second geometries at different Reynolds numbers, porosities and volumetric fractions:
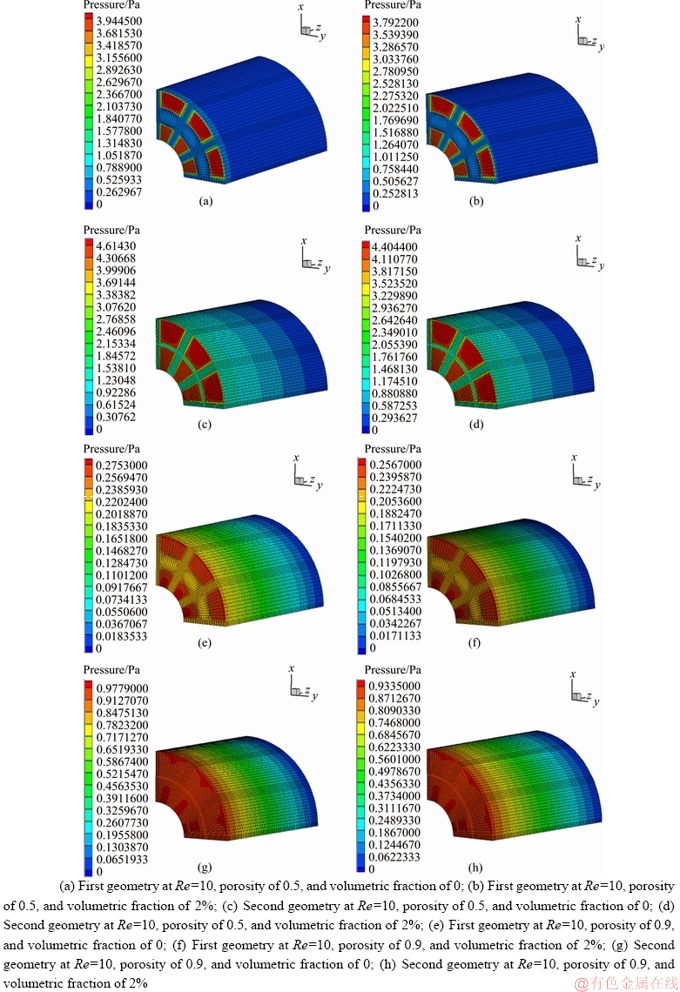
Figure 19 Pressure contour for first and second geometries at different Reynolds numbers, porosities and volumetric fractions:
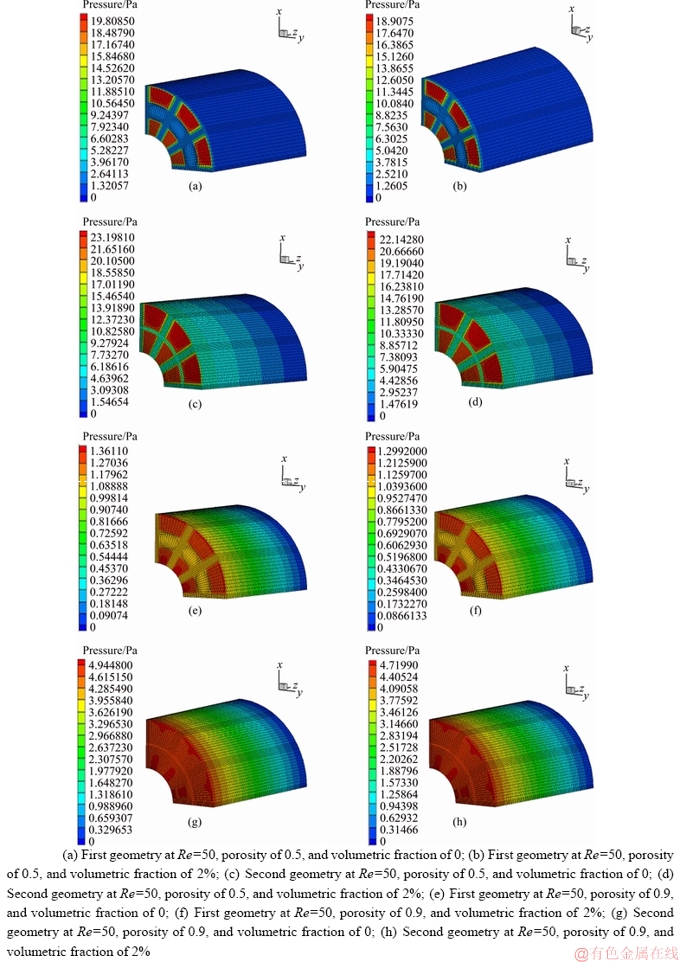
Figure 20 Pressure contour for first and second geometries at different Reynolds numbers, porosities and volumetric fractions:
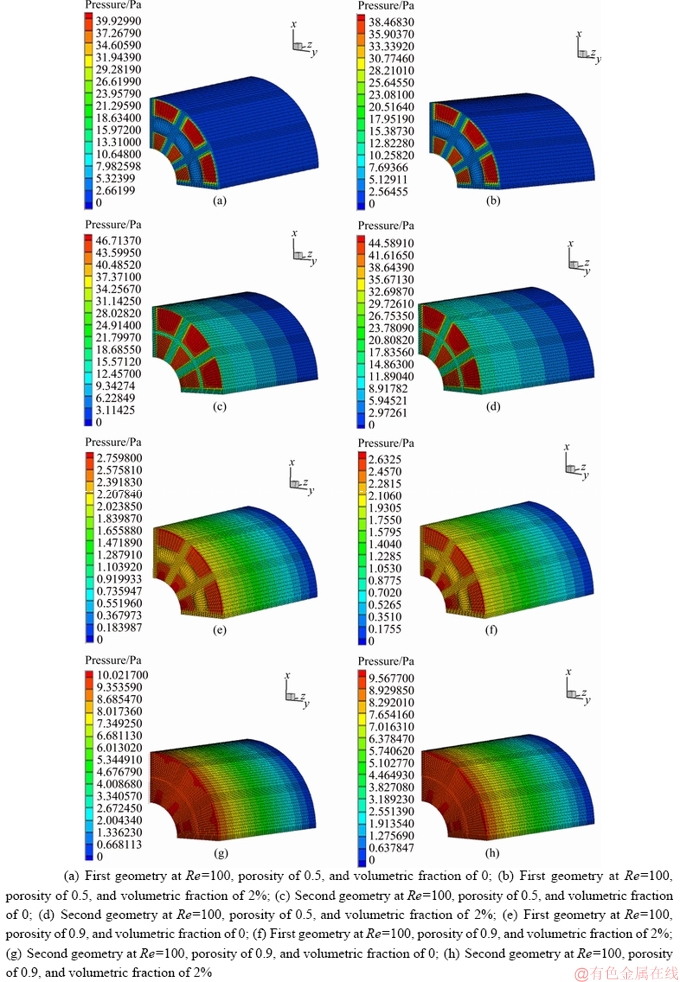
Figure 21 Pressure contour for first and second geometries at different Reynolds numbers, porosities and volumetric fractions:
3.5 Performance evaluation criterion (PEC) for nanofluid
The diagram of performance evaluation criterion (PEC) with respect to volumetric fraction at a porosity of 0.5 for the first geometry is demonstrated in Figure 22. Based on Eq. (14), this criterion is defined as the ratio of transferred heat to the required pumping power,
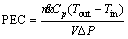 (14)
(14)
According to the figure, the PEC assumes higher values at lower Reynolds numbers, where more heat is transferred with respect to the required pumping power. Moreover, at lower Reynolds numbers, the exchange of heat between the pipe surface and the nanofluid takes longer durations, which in turn allows more heat to be absorbed and transferred from the pipe surface. Comparison between the mean PEC values at volumetric fractions ranging from 0 to 5% shows that, by decreasing the Reynolds number from 25, 50, 75, and 100 to 10, the PEC values increase by 3.6, 13.6, 27.5, and 45.6 times, respectively. As demonstrated in the pressure contours, the pressure difference between the pipe inlet and outlet is multiplied at high Reynolds numbers, indicating that the PEC is directly proportional to the temperature difference and inversely related to the pressure difference. The diagram of PEC with respect to the Reynolds number at different volumetric fractions and a porosity of 0.5 for the first geometry are shown in Figure 23. The PEC assumes higher values at higher volumetric fractions, indicating that increasing the volumetric fraction of nanoparticles in the base fluid results in an increased heat transfer rate. This increase is higher than that of the pumping power at these volumetric fractions. Considering that a lower pumping power is required at a volumetric fraction of zero, the heat transfer rate at this volumetric fraction is lower than that of higher volumetric fractions and, as a result, the PEC is reduced at this volumetric fraction. Comparison of the PEC values for volumetric fractions ranging from 0 to 5% at Reynolds numbers of 10 to 100 suggests that compared to a volumetric fraction of zero, the PEC values increase from 4% to 20% by increasing the volumetric fraction from 0.2% to 5%.
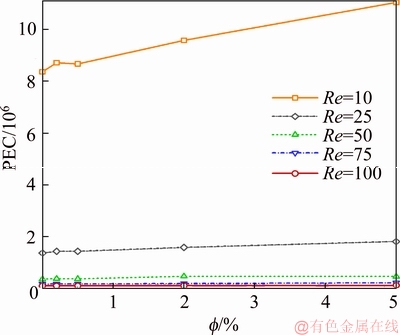
Figure 22 PEC with respect to volumetric fraction at different Reynolds numbers and a porosity of 0.5 for first geometry
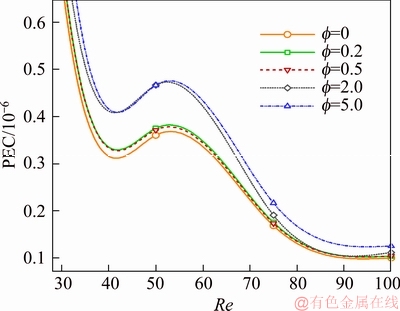
Figure 23 PEC with respect to Reynolds number at different volumetric fractions and a porosity of 0.5 for first geometry
Diagram of PEC with respect to volumetric fraction at different Reynolds numbers and porosity of 0.5 for the second geometry is shown in Figure 24. The PEC values increase by 6, 23, 50, and 86 times by increasing the Reynolds number from 10 to 25, 50, 75, and 100, respectively.

Figure 24 PEC with respect to volumetric fraction at different Reynolds numbers and a porosity of 0.5 for second geometry
Comparison of the mean PEC values in the first and second geometries at a porosity of 0.5 suggests that the values of this criterion in the first geometry are roughly twice those of the second geometry at all Reynolds numbers. Since PEC is inversely related to pressure difference, this criterion is decreased as the pressure difference between the pipe inlet and outlet is increased. Therefore, in the second geometry, where the temperature difference between the inlet and outlet is almost twice that of the first geometry, the PEC is decreased by the same ratio compared to the first geometry.
Diagram of PEC with respect to Reynolds number at different volumetric fractions and porosity of 0.5 for the second geometry is shown in Figure 25. Comparison of the PEC values at volumetric fractions ranging from 0 to 5% and Reynolds numbers of 10 to 100 shows that this criterion is increased from 4% to 23% by increasing the volumetric fraction from 0.2 to 5 compared to the volumetric fraction of zero. The results reveal that the increase in the PEC values at volumetric fractions of 0.2% to 5% is almost constant compared to the volumetric fraction of zero.
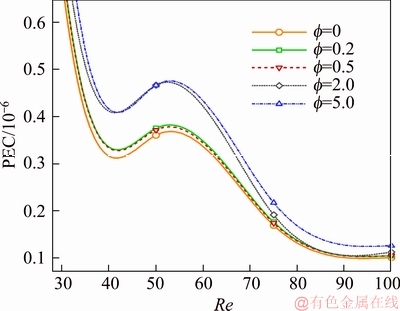
Figure 25 PEC with respect to Reynolds number at different volumetric fractions and a porosity of 0.5 for second geometry
3.6 Performance evaluation criterion (PEC) in porous medium
Employing a porous medium increases the heat transfer rate as well as the pressure drop and pumping power. The thermal performance evaluation criterion expresses the relation between the increase in the heat transfer rate with respect to the simultaneous increase in the pressure drop and pumping power in a porous medium and is defined as follows (Eq. (15)):
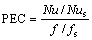 (15)
(15)
where the parameters (Nusselt number and pressure drop coefficient) with and without the index s are, respectively, associated with the channels without and with porous media. Diagram of thermal performance evaluation criterion with respect to Reynolds number at porosities of 0.5 and 0.9 and volumetric fraction of zero is demonstrated in Figure 26 for the first and second geometries. PEC values lower than one (PEC<1) indicate that the increase in pressure drop is larger than the increase in the heat transfer rate when a porous medium is used. PEC values larger than 1 (PEC>1) show that use of the porous medium in the heat transfer process is desirable, since the increase in heat transfer is greater than that of the pressure drop in this medium. According to the figure, compared to porosity of 0.5, a porosity of 0.9 is more desirable in the heat transfer process for both geometries, since a lower pressure drop is achieved in porous media with higher porosities. The highest PEC values are associated with the second geometry at a porosity of 0.9. In the second geometry, where a larger cross-sectional area of the pipe is filled with porous medium, the increase in the heat transfer rate is higher than the pressure drop in the porous medium. At the same porosity and in the first geometry where a larger free area is available for the fluid to pass (with no porous medium), the heat transfer rate is decreased due to the reduction in the area covered by the porous medium across the pipe cross-section. The fluid flow is more resisted by the porosity of 0.5 compared to the porosity of 0.9. Therefore, compared to the second geometry, the first geometry has a better condition since it comprises a larger free surface (with no porous medium) available for the fluid to pass. According to the diagrams, the PEC assumes larger values at higher Reynolds numbers. Comparison of the PEC values at Reynolds numbers of 10, 50, and 100 shows that the values of this coefficient in both geometries and at both porosities increase by 10% and 60% by increasing the Reynolds number from 50 and 10 to 100, respectively. The diagram of thermal PEC with respect to Reynolds number at porosities of 0.5 and 0.9 and a volumetric fraction of 2% are shown in Figure 27 for the first and second geometries. The aforementioned explanations on Figure 26 also apply to this figure. Comparison of Figures 26 and 27 shows that, the volumetric fraction of nanoparticles does not significantly affect the thermal PEC of the porous medium. The slight reduction (about 2.5%) in the thermal PEC of the porous medium at volumetric fraction of 2% compared to volumetric fraction of zero is due to the passage of nanoparticles through the porous medium, which consequently increases the pressure drop and pumping power.
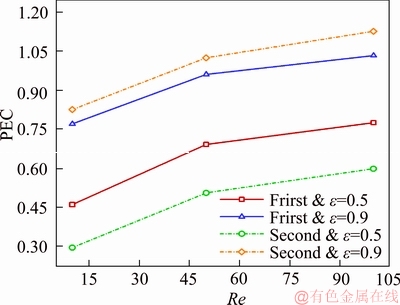
Figure 26 PEC at different Reynolds numbers at porosities of 0.5 and 0.9 for first and second geometries
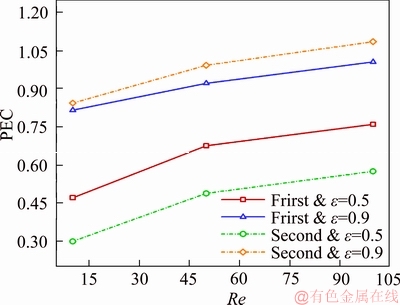
Figure 27 PEC at different Reynolds numbers at porosities of 0.5 and 0.9 for first and second geometries
4 Conclusions
In this paper, we investigated the laminar heat transfer and nanofluid flow between two porous horizontal concentric cylinders. The following results can be deduced from our numerical investigation:
1) Compared to the first geometry, the convective coefficient in the second geometry increases by 8.3%, 7% and 5.5 % at Reynolds numbers of 100, 75, and 50, respectively.
2) The convective coefficients of the first geometry at Reynolds numbers of 100, 75, 50, and 25 increased by 11.3%, 10%, 8% and 4.5% compared to the second geometry, respectively.
3) Comparison of the outlet temperatures for two heat fluxes of 300 and 1200 W/m2 indicates a 2.5% temperature growth by a fourfold increase in the heat fluxes.
4) The higher Nusselt number is associated with the second geometry occurring at porosities of 0.9 and 0.5, respectively. In both geometries, the Nusselt number values at the porosity of 0.9 are higher, which is due to the increased nanofluid convection at higher porosities.
5) The velocity of the nanofluid experiences a two-fold increase at the outlet compared to its inlet velocity in the first geometry and for both porosities. Similarly, a three-fold increase was achieved in the second geometry and for both porosities.
References
[1] HEMMAT ESFE M, HASSANI AHANGAR M R, REJVANI M, TOGHRAIE D, HAJMOHAMMAD M H. Designing an artificial neural network to predict dynamic viscosity of aqueous nanofluid of TiO2 using experimental data [J]. Int Commun Heat Mass Transf, 2016, 75: 192–196.
[2] AFRAND M, TOGHRAIE D, SINA N. Experimental study on thermal conductivity of water-based Fe3O4 nanofluid: Development of a new correlation and modeled by artificial neural network [J]. Int Commun Heat Mass Transf, 2016, 75: 262-269.
[3] ZARRINGHALAM M, KARIMIPOUR A, TOGHRAIE D. Experimental study of the effect of solid volume fraction and Reynolds number on heat transfer coefficient and pressure drop of CuO–water nanofluid [J]. Exp Therm Fluid Sci, 2016, 76: 342-351.
[4] SAJADIFAR S A, KARIMIPOUR A, TOGHRAIE D. Fluid flow and heat transfer of non-Newtonian nanofluid in a microtube considering slip velocity and temperature jump boundary conditions [J]. European Journal of Mechanics- B/Fluids, 2017, 61: 25-32.
[5] NAZARI S, TOGHRAIE D. Numerical simulation of heat transfer and fluid flow of water-CuO nanofluid in a sinusoidal channel with a porous medium [J]. Physica E: Low-dimensional Systems and Nanostructures, 2017, 87: 134-140.
[6] FARIDZADEH M R, SEMIROMI D T, NIROOMAND A. Analysis of laminar mixed convection in an inclined square lid-driven cavity with a nanofluid by using an artificial neural network [J]. Heat Transfer Research, 2013, 45(4): 361-390.
[7] ESFAHANI M A, TOGHRAIE D. Experimental investigation for developing a new model for the thermal conductivity of Silica/Water-Ethylene glycol (40%-60%) nanofluid at different temperatures and solid volume fractions [J]. Journal of Molecular Liquids, 2017, 232: 105-112.
[8] AGHANAJAFI A, TOGHRAIE D, MEHMANDOUST B. Numerical simulation of laminar forced convection of Water-CuO nanofluid inside a triangular duct [J]. Physica E: Low-dimensional Systems and Nanostructures, 2017, 85: 103-108.
[9] ZADKHAST M, TOGHRAIE D, KARIMIPOUR A. Developing a new correlation to estimate the thermal conductivity of MWCNT-CuO/water hybrid nanofluid via an experimental investigation [J]. Journal of Thermal Analysis and Calorimetry, 2017, 129(2): 859-867. DOI: 10.1007/s10973-017-6213-8.
[10] HEMMAT ESFE M, AFRAND M, YAN W M, YARMAND H, TOGHRAIE D, DAHARI M. Effects of temperature and concentration on rheological behavior of MWCNTs/SiO2 (20–80)-SAE40 hybrid nano-lubricant [J]. Int Commun Heat Mass Transf, 2016, 76: 133-138.
[11] AFRAND M, TOGHRAIE D, RUHANI B. Effects of temperature and nanoparticles concentration on rheological behavior of Fe3O4–Ag/EG hybrid nanofluid: An experimental study [J]. Exp Therm Fluid Sci, 2016, 77: 38-44.
[12] HEMMAT ESFE M, YAN W M, AFRAND M, SARRAF M, TOGHRAIE D, DAHARI M. Estimation of thermal conductivity of Al2O3 /water(40%)–Ethylene-glycol (60%) by artificial neural network and correlation using experimental data [J]. Int Commun Heat Mass Transf, 2016, 74: 125-128.
[13] TOGHRAIE D, CHAHARSOGHI V A, AFRAND M. Measurement of thermal conductivity of ZnO–TiO2/EG hybrid nanofluid [J]. J Therm Anal Calorim, 2016, 125(1): 527-535. http://dx.doi.org/10.1007/s10973-016-5436-4.
[14] TOGHRAIE D, ALEMPOUR S M B, AFRAND M. Experimental determination of viscosity of Water based magnetite nanofluid for application in heating and cooling systems [J]. Journal Magnetism and Magnetic Materials, 2016, 417: 243-248.
[15] HEMMAT ESFE M, SAEDODIN S, WONGWISES S, TOGHRAIE D. An experimental study on the effect of diameter on thermal conductivity and dynamic viscosity of Fe/water nanofluids [J]. Therm Anal, 2015, 119(3): 1817-1824. DOI: 10.1007/s10973- 014-4328-8
[16] HEMMAT ESFE M, AFRAND M, GHAREHKHANI S, ROSTAMIAND H, TOGHRAIE D, DAHARI M. An experimental study on viscosity of alumina-engine oil: Effects of temperature and nanoparticles concentration [J]. Int Commun Heat Mass Transf, 2016, 76: 202-208.
[17] MAGHREBI M J, NAZARI M, ARMAGHANI T. Forced convection heat transfer of nanofluids in a porous channel [J]. Transp Porous Med, 2012, 93: 401-413.
[18] SHEIKHOLESLAMI M, GANJI D D, ROKNI H B. Nanofluid flow in a semi-porous channel in the presence of uniform magnetic field [J]. IJE TRANSACTIONS C: Aspects, 2013, 26(6): 653-662.
[19] SALEH M H. Laminar free convection of nanofluid flow in horizontal porous annulus [J]. World Academy of Science, Engineering and Technology, International Journal of Mechanical and Mechatronics Engineering, 2013, 7(6): 1306-1313.
[20] MAHDI R A, MOHAMMED H A, MUNISAMY K M. Improvement of convection heat transfer by using porous media and nanofluid: Review [J]. International Journal of Science and Research, 2013, 2(8): 34-48.
[21] ARMAGHANI T, ALI J. CHAMKHA, MAGHREBI M J, NAZARI M. Numerical analysis of a nanofluid forced convection in a porous channel: A new heat flux model in LTNE condition [J]. Journal of Porous Media, 2014, 17(7): 637-646.
[22] PAL D, MANDAL G, VAJRAVALU K. Mixed convection stagnation-point flow of nanofluids over a stretching/ shrinking sheet in a porous medium with internal heat generation/absorption [J]. Communications in Numerical Analysis, 2015(1): 30-50.
[23] SHEIKHOLESLAMI M, MUSTAFA M T, GANJI D D. Nanofluid flow and heat transfer over a stretching porous cylinder considering thermal radiation [J]. Iranian Journal of Science & Technology, 2015, 39A3 (Special issue): 433-440.
[24] ZEHFOROOSH A, HOSSAINPOUR S. Investigation of Brownian motion of CuO-water nanofluid in a porous cavity with internal heat generation by using of LTNE model [J]. J Nano Struct, 2015, 5(3): 237-250.
[25] NOJOOMIZADEH M, KARIMIPOUR A. The effects of porosity and permeability on fluid flow and heat transfer of multiwalled carbon nano-tubes suspended in oil (MWCNT/Oil nano-fluid) in a microchannel filled with a porous medium, Physica E, 2016, 84: 423-433.
[26] TU Wen-bin, WANG Yun, TANG Yong. Thermal characteristic of a tube fitted with porous media inserts in the single phase flow [J]. International Journal of Thermal Sciences, 2016, 110: 137-145.
[27] KASAEIAN A, AZARIAN R D, MAHIAN O, KOLSI L, ALI J. Chamkha, Somchai Wongwises, Ioan Pop. Nanofluid flow and heat transfer in porous media: A review of the latest developments [J]. International Journal of Heat and Mass Transfer, 2017, 107: 778-791.
[28] MOJUMDER S, SAHA S, RAHMAN M R, RAHMAN M M, RABBI K M, IBRAHIM T A. Numerical study on mixed convection heat transfer in a porous L-shaped cavity [J]. Engineering Science and Technology, an International Journal, 2017, 20: 272-282.
[29] BIANCO V, MANCA O, NARDINI S, VAFAI K. Heat transfer enhancement with nano fluids [M]. Boca Raton: CRC Press, 2015.
[30] ZHAO Ning-bo, YANG Jia-long, LI Hui, ZHANG Zhi-ying, LI Shu-ying. Numerical investigation of laminar heat transfer and flow performance of Al2O3-water nanofluids in a flat tube [J]. Int J of Heat and Mass Transfer, 2016, 92: 268-272.
[31] ERGUN S. Fluid flow through packed columns [J]. Chem Eng Prog, 1952, 48: 89-94.
(Edited by HE Yun-bin)
中文导读
两个多孔水平同心圆柱间的层流传热和纳米流体流动的数值研究
摘要:研究了在Re=10,25,50,75,100和铜纳米粒子体积分数分别为0, 0.2%,0.5%,2%和5%,多孔介质孔隙率分别为0.5和0.9条件下多孔水平同心圆柱间的层流传热和纳米流体流动。在雷诺数分别为100、75和50时,与第一种几何形式相比,第二种几何形式的对流系数分别增加了8.3%、7%和5.5%。对300和1200 W/m2两种热通量的出口温度进行比较,发现热通量增加4倍,温度增加了2.5%。此外,较高的Nusselt数与第二种几何形状相关,分别出现在0.9和0.5的孔隙度。在这两种几何结构中,孔隙度为0.9时的Nusselt数值较高,这是由于孔隙度较高时纳米流体对流增加所致。在第一几何形状和孔隙度下,纳米流体的出口的速度比进口速度增加2倍。同样,在第二个几何图形和两个孔隙度上都实现3倍的增长。
关键词:多空水平同心圆柱体;纳米流体;磁导率;传热
Received date: 2018-03-17; Accepted date: 2018-11-11
Corresponding author: Davood TOGHRAIE, PhD; Tel: +98-3133660011; E-mail: toghraee@iaukhsh.ac.ir; ORCID: 0000-0003-3344-8920

