J. Cent. South Univ. Technol. (2008) 15(s1): 550-554

DOI: 10.1007/s11771-008-419-7

Equilibrium position of misfit dislocation dipole and critical parameters of buried strained nanoscale inhomogeneity in system of viscoelastic matrix

LIU You-wen(刘又文), XIE Chao(谢 超), FANG Qi-hong(方棋洪)

(College of Mechanics and Aerospace, Hunan University, Changsha 410082, China)

Abstract: A theoretical model was suggested which describes the generation of the misfit dislocation dipole in the system of the viscoelastic matrix containing a circular stiff nanoscale inhomogeneity. The critical condition of misfit dislocation dipole and the solution of equilibrium position were given. The influence of the ratio of shear modulus, the misfit strain and viscosity on the equilibrium of the dislocation and critical parameter of inhomogeneity was investigated. The result shows that the equilibrium position d_e increases with the increase of the ratio of original shear modulus and the effect decreases with the increase of viscosity of matrix. Along with the increase of viscosity of matrix, d_e first increases and then decreases and possesses maximum value when t=0.3τ and tends to a stable value when t≥1.0τ. Along with the increase of viscosity of matrix, R_c first decreases and then increases and possesses minimum value when t=0.3τ and tends to a stable value when t≥1.0τ.

Key words: nanoscale inhomogeneity; viscoelastic; misfit strain; misfit dislocation dipole; critical condition

1 Introduction

Recently, much attention has been paid to the investigation of nanocomposites which contain more than one solid phase and where at least one of the phases has a dimension of less than 100 nm. Because of their unique properties, the nanocomposites become important both in theoretical and applied research^[1].

The influence of misfit stresses arising due to a misfit between the crystal lattices of the adjacent component phases on structure and properties of nanocomposites is very strong. A partial relaxation of misfit stresses often leads to the generation of misfit dislocations at interfaces in thin-film and bulk nanocomposites^[2-3] .

Generally speaking, the generation of misfit dislocations have deleterious influence on material properties, controlling the generation of misfit dislocations in manufacturing can minimize the defects of product^[4]. Therefore, researching the discipline of the generation of misfit dislocations is very important.

The investigation of the critical conditions is an important method which can control the generation of misfit dislocations. Recently, the study of it has become very popular. The formation of misfit dislocations (MDs) parallel to axis of nanowires has been studied in triangular cross sections^[5], circular cross sections^[6], and rectangular cross  sections^[7]. The mechanism for the nucleation of dislocation dipoles at nanoparticles in nanocomposite solids is suggested by OVID’KO and SHEINERMAN^[8]. A number of experimental observations of MDs demonstrate that the core of the dislocation is not always located at the interface, but is displaced some distance into the elastically softer phase^[9]. The solutions of critical conditions of the generation for misfit dislocation dipoles and critical parameters of buried strained nanoscale inhomogeneity have been obtained by FANG et al^[10]. The previous researches are unrelated with the influence of material viscosity on the equilibrium position of misfit dislocation dipole and critical parameters of buried strained nanoscale inhomogeneity in the system of matrix. However, most materials have viscosity, especially in manufacturing nanocomposites.

The equilibrium position of misfit dislocation dipole and critical parameters of buried strained nanoscale inhomogeneity in the system of the viscoelastic matrix is investigated in this work. The critical condition of misfit dislocation dipole and the solution of equilibrium position are given. The influence of the ratio of shear modulus, the misfit strain and the solution of equilibriumposition are given. The influence of the ratio of shear modulus, the misfit strain and viscosity on the equlibrium of the dislocation and critical parameter of inhomogeneity is investigated.

2 Elasticity-viscoelasticity correspondence principle

As shown in Fig.1, the viscoelastic properties of materials can be simulated by a group containing springs and damping. In this paper, we adopt the standard linear model to simulate the mechanical behavior of viscoelastic materials^[11].

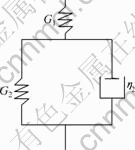
Fig.1 Standard linear model of viscoelaticity

Stress—strain relationship

(a₁D+1)s_ij=(b₁D+b₀)e_ij                         (1)

where

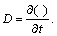
Equivalent shear modulus

                 (2)

Shear relaxation modulus

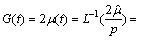
            (3)

Shear creep compliance

       (4)

where  L^-1 denotes inverse Laplace transformation; μ₀=G₁, μ_∞=G₁G₂/(G₁+G₂). The relaxation time of shear relaxation modulus is shown as τ_ε=η₂/(G₁+G₂), and the delaytime of shear creep compliance is shown as τ=η₂/G₂. It can be also shown as τ=(μ₀/μ_∞)τ_ε. We define that, all stresses and strains are zero before t=0 and  is the shear modulus of elastic problem in the field of Laplace transformation.

3 Problem description

As shown in Fig.2, the system of the viscoelastic matrix contains a cylindrical stiff nanoscale inhomogeneity whose radius is R. Let inhomogeneity with shear modulus μ_i occupy region S⁺, while matrix with shear modulus μ_m(t) occupy region S^-. The misfit dislocation dipole consists of a positive screw dislocation with Burgers vector b₃ at x₁(=R+d) and a negative screw dislocation with Burgers vector -b₃ at x₂(=-R-d). Their lines are parallel with the axis of cylindrical inhomogeneity. The lattice mismatch strain can be treated as eigenstrain ε_m.

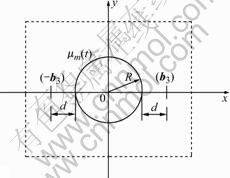
Fig.2 MD dipole in composite containing nanoscale inhomogeneity

4 Equilibrium position of MDs dipole and critical parameters of nanoscale inhomogeneity

We define that, when materials in the raw are in the initial stage, namely t=0, all stresses and strains are zero.

Let analytical function F(z)=f′(z). In the field of Laplace transformation, the field of displacement and stress in regions S⁺ and S^- can be expressed as

                                (5)

                           (6)

where  and  denote displacement and stresses of elastic problem in the field of Laplace transformation, respectively.

Following the work of GUTKIN et al^[12], the generation of the MD dipole is allowed if the total-energy variation is calculated from the inclusion and matrix configuration free of dislocations is negative

≤0                           (7)

where   denotes the elastic energy of the MD dipole in the inclusion and matrix system and  is the elastic energy associated with the elastic interaction between the MD dipole and the misfit stress.

Following the work of HIRTH and LOTHE^[13], can be expressed as

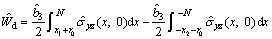  (8)

where  N is the distance corresponding to the material size and r₀ is the core radius of the dislocation. One may take N→∞ for all terms in the integral. Following the work of FANG et al^[10], the stress component can be easily derived.

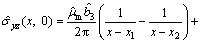
        (9)

where 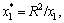  x₁=R+d, x₂=-R-d.

Substituting Eqn.(9) into Eqn.(8), can be expressed as

                                          (10)

Taking inverse Laplace transformation of Eqns.(9) and (10), the viscoelastic stress and energy can be obtained.

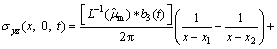
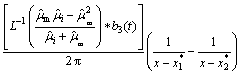 (11)

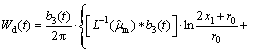
 (12)

where  “*” denotes convolution.

The elastic energy of the interaction between the MD dipole and the misfit stress field is given by

(13)

where 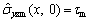 denotes to be misfit stress. Following the work of FANG et al^[10], the stress is expressed as

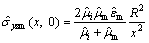                    (14)

Substituting Eqn.(14) into Eqn.(13), the elastic energy can be obtained.

                    (15)

Taking inverse Laplace transformation of Eqs.(14) and (15), the viscoelastic stress and energy can be obtained.

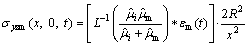     (16)

   (17)

Substituting Eqs.(10) and (15) into Eq.(7), the total energy can be obtained.

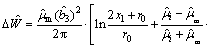
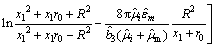≤0  (18)

Taking inverse Laplace transformation of Eqn.(18), the total energy can be obtained.

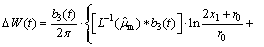
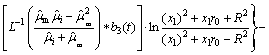
≤0    (19)

The total force acting on the positive screw dislocation component arises from three factors: 1) the interaction between the positive screw dislocation and interface (f_i), 2) the interaction between two screw dislocations (f_d), 3) the interaction between dislocation and the misfit stress in the matrix (f_m). The total force f_x=f_i+f_d+f_m can be calculated by using elasticity method and is given as follows:

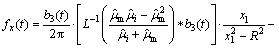
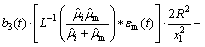
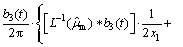
      (20)

where Let b₃(t)=b₃?H(t), ε_m(t)=ε_m?H(t) (H(t) denotes unit step function).

When the dislocation locates at the critical equilibrium position, the total force acting on dislocation is zero.

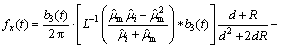
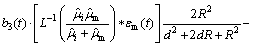
=0 (21)

In view of R＞＞ d, the critical parameters of inhomogeneity R_c and equilibrium position d_e of MDs can be obtained from Eqns.(19) and (21).

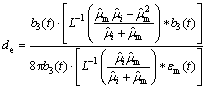           (22)

If the matrix is elastic, namely t=0, Eqn.(22) can be reduced to

                           (23)

which matches the result of FANG et al^[10].

The critical parameters of nanoscale inhomogeneity can be calculated from ?W(t)=0 in Eqn.(19).

Assume the material of matrix is epoxy resin, with t=0, E₀=3.4 GPa, v₀=0.3, μ₀=E₀/[2(1+v₀)].

The equilibrium position of misfit dislocation is normalized as d₀=d_e/b₃. The variation of normalized equilibrium position d₀ with normalized time t/τ for different eigenstrain ε_m is shown in Fig.3, when α=μ₀/μ_m0=10 and μ_i/μ_m0=β=1 (μ_m0 is shear modulus of matrix at t=0). The value of equilibrium position d₀ decreases with the increase of eigenstrain. Along with the increase of viscosity of matrix, d₀ first increases and then decreases and possesses the maxium value when t=0.3τ and tends to be a stable value when t≥1.0τ.

The variation of normalized equilibrium position d₀ with the ratio of shear modulus μ_i/μ_m0=β for different moment t/τ is shown in Fig.4, when α=μ₀/μ_m=10 and ε_m=0.006. The equilibrium position d₀ increases with the increase of β and the effect decreases with the increase of viscosity of matrix.

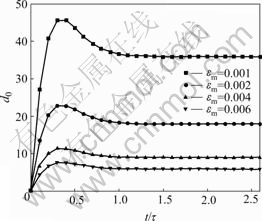
Fig.3 Variation of normalized equilibrium position d₀ with normalized time t/τ

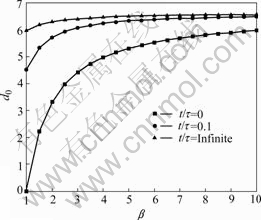
Fig.4 Variation of normalized equilibrium position d₀ with ratio of shear modulus β

The parameter of inhomogeneity is normalized as R₀=R/b₃ and the elastic energy is normalized as

                      (24)

The variation of normalized elastic energy ΔW₀ with R₀ for different viscosity of matrix is shown in Fig.5, when α=μ₀/μ_m=10, r=0.5b₃, μ_i/μ_m0=β=1 and ε_m=0.004. When ΔW₀=0, R₀ possesses the critical value R_c. Along with the increase of viscosity of matrix, the critical parameter of inhomogeneitiy R_c first decreases and then increases and possesses the minium value when t/τ=0.3 and tends to a stable value when t/τ≥1.0.

The equilibrium position of misfit dislocation dipole and critical parameters of buried strained nanoscale inhomogeneity in the system of viscoelastic matrix is investigated. The critical condition of misfit dislocation dipole and the solution of equilibrium position are given.

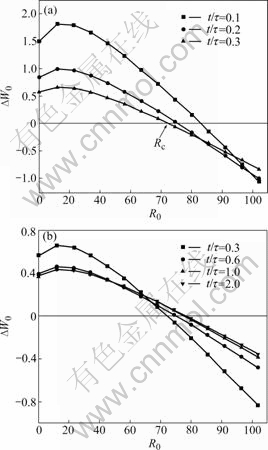
Fig.5 Variation of normalized elastic energy ΔW₀ with R₀

The influence of the ratio of shear modulus, misfit strain and viscosity on the equilibrium of the dislocation and critical parameter of inhomogeneity is investigated. The result shows that the equilibrium position d_e increases with the increase of the ratio of original shear modulus and the effect decreases with the increase of viscosity of matrix. Along with the increase of viscosity of matrix, d_e first increases and then decreases, and possesses maximum value when t=0.3τ and tends to a stable value when t≥1.0τ. Along with the increase of viscosity of matrix, R_c first decreases and then increases and possesses minimum value when t=0.3τ and tends to a stable value when t≥1.0τ.

[1] LINK S, EI-SAYED M A. Optical properties and ultrafast dynamics of metallic nanocrystals [J]. Annu Rev Phys Chem, 2003, 54: 331-336.

[2] ZHANG T Y, SU Y J. The critical thickness of an epilayer deposited on a semiconductor-on-insulator compliant substrate [J]. Appl Phys Lett, 1999, 74: 1689.

[3] AIFANTIS K E, KOLESNIKOVA A L, ROMANOV A E. Nucleation of misfit dislocations and plastic deformation in core/shell nanowires [J]. Philos Mag, 2007, 87(30): 4731-4757.

[4] KASSNER M E, NEMAT-NASSER S, SUO Z, BAO G. New directions in mechanics [J]. Mech Mater, 2005, 37: 231-259.

[5] FREUND L B, GOSLING T J. Critical thickness condition for growth of strained quantum wires in substrate V-grooves [J]. Appl Phys Lett, 1995, 66: 2822.

[6] COLIN J, GRIHLE J. Dipole of misfit dislocations in axially symmetric structures [J]. Philos Mag Lett, 2002, 82(3): 125-132.

[7] GUTKIN M Y, OVID’KO I A, SHEINERMAN A G. Misfit dislocations in composites with nanowires [J]. J Phys: Condens Matter, 2003, 15: 3539-3554.

[8] OVID’KO I A, SHEINERMAN A G. Nanoparticles as dislocation sources in nanocomposites [J]. J Phys: Condens Matter, 2006, 18: L225.

[9] WU X, WEATHERLY G C. The first stage of stress relaxation in tensile strained In_1-xGa_xAs_1-yP_y films [J]. Philos Mag A, 2001, 81(6): 1489-1506.

[10] FANG Q H, LIU Y W, CHEN J H. Misfit dislocation dipoles and critical parameters of buried strained nanoscale inhomogeneity [J]. Appl Phys Lett, 2008, 92: 1.

[11] ZHANG Chun-yuan. Viscoelastic fracture mechanics [M]. Wuhan: Huazhong University of Science and Technology Press, 1994. (in Chinese)

[12] GUTKIN M Y, OVID’KO I A, SHEINERMAN A G. Misfit dislocations in composites with nanowires [J]. J Phys: Condens Matter, 2000, 12: 5391.

[13] HIRTH J P, LOTHE J. Theory of dislocations[M]. New York: Wiley, 1982.

(Edited by YUAN Sai-qian)

Foundation item: Project(10472030) supported by the National Natural Science Foundation of China

Received date: 2008-06-25; Accepted date: 2008-08-05

Corresponding author: LIU You-wen, Professor; Tel: +86-731-8822330; E-mail: Liuyouwen4810@sina.com