一种新的水平电偶极子电磁波场区划分方法

程辉¹，李帝铨²

(1. 湖南科技大学 先进矿山装备教育部工程研究中心，湖南 湘潭，411201；

2. 中南大学 地球科学与信息物理学院，有色金属成矿预测教育部重点实验室，湖南 长沙，410083)

摘要：为了推动有源电磁法的场区划分由定性向定量发展，提出一种新的可控源电磁法场区划分方法。定义电场强度E_x、磁场强度H_y和阻抗Z_xy的衰减率，计算分析均匀半空间和2层模型的轴向和赤道模式E_x、H_y和Z_xy的衰减率，揭示水平电偶极子源电磁波衰减率随收发距(感应数)的变化规律；基于均匀半空间E_x，H_y和Z_xy的衰减率进行场区划分，讨论E_x，H_y和Z_xy衰减率在不同场区的衰减特性。研究结果表明：轴向和赤道模式下的E_x，H_y和Z_xy衰减特征有较大区别；当衰减率容许误差为1‰时，轴向模式下E_x，H_y和Z_xy进入远区的感应数分别为11.450，6.994和12.294，进入远区的顺序为H_y，E_x，Z_xy；在赤道模式下，E_x，H_y和Z_xy进入远区的感应数分别为9.198，9.924和10.915，进入远区的顺序为E_x，H_y，Z_xy。

关键词：水平电偶极子；衰减系数；场区划分；电磁勘探；可控源电磁法

中图分类号：P631           文献标志码：A         文章编号：1672-7207(2014)07-2250-09

A new electromagnetic field division method for horizontal electric dipole

CHENG Hui¹, LI Diquan²

(1. Engineering Research Center for Advanced Mining Equipment, Ministry of Education,

Hunan University of Science and Technology, Xiangtan 411201, China;

2. School of Geosciences and Info-Physics, Key Laboratory of Metallogenic Prediction of Nonferrous Metals,

Ministry of Education, Central South University, Changsha 410083, China)

Abstract In order to promote the development of EM fields’ division method from qualitative to quantitative, a novel method for CSEM (control source electromagnetic method) fields’ division was proposed. A new attenuation rate was defined for electric field strength E_x, magnetic field strength H_y, and impedance Z_xy. Based on the new attenuation rate, the propagation characteristics of E_x, H_y and Z_xy were studied, and the attenuation rate change of the HED (horizontal electric dipole) source electromagnetic wave with the change of the offset (induction number) was revealed. Based on the attenuation rate of E_x, H_y and Z_xy which was calculated by homogeneous half space model, the EM fields’ division was proposed. The attenuation characteristic in near field, transition field and far field was studied. The results show that there is difference between equatorial and axial mode in EM fields’ attenuation. The induction numbers of E_x, H_y and Z_xy are 11.450, 6.994, 12.294 when they change into far field in axial direction. The induction numbers of E_x, H_y and Z_xy are 9.198, 9.924 and 10.915, respectively, when they change into far field in equator direction.

Key words: horizontal electric dipole; attenuation coefficient; field zones division; electromagnetic exploration; CSEM

据CSEM(controlled source electromagnetic method)理论，按传播途径，电磁波可分为天波、地面波和地层波三种。电磁波在传播过程中，依据接收点与发射源的距离可划分为3个区域：近区、过渡区和远区。远区场的物理含义是地面波占主导地位的场区；近区场的物理含义是地层波占主导地位的场区；过渡场是电磁波中的地面波和地层波成分相当的场区。实际上，地面波和地层波均与地质体发生电磁作用，但是否都影响到地面观测值或哪种波占主导，这3个场区之间的边界位置与大地电阻率、发射信号的频率等参数有关^[1-13]。在CSEM的研究中，有很多关于近区场、过渡区场和远区场特征的探讨和研究，对各种激励的各个电磁场分量探测能力进行了分析，并形成了多种有源电磁法，如可控源音频大地电磁法^[14-18]、磁偶源频率测深法^[19]、极低频电磁法^[20-23]、广域电磁法^[24-25]、瞬变电磁法^[26-28]等。但众多涉及到近区、过渡区和远区划分的探讨也只是处于定性阶段，大部分都是通过电磁场的特征分析和总结得到的结论，没有形成统一的划分标准。在CSAMT (controlled source audio- frequency magnetotelluric method)的研究中，主要存在2种场区划分方法：一种是以感应数划分，感应数p是收发距r相对趋肤深度的比值，p ＜＜ 1时为近区，p ＞＞ 1时为远区，时为过渡区^[2-3]；一种是以收发距与勘探深度的比值划分，以收发距r与波长或与频率f的关系来划分波区和S区，并在考虑勘探深度后，划分近区和远区，在实际生产中具有一定的指导意义^{[4, 6]}。此外，还有以定义近区和远区，当＜＜ 1为近区，当＞＞ 1为远区，这与感应数方法划分结果是互通的，可看作感应数方法的变种。上述方法均缺乏精确的定义，存在模糊的界限，划分结果往往因人而异，在理论研究和实际施工中存在较多问题^{[4, 6]}。除以上场区划分方法外，尚未见精确的划分方法。针对以上问题，本文作者对水平电偶极源电磁波的传播特性进行研究，计算电磁波的衰减率，以提出更合理的近区、过渡区和远区的区划方法，以便完善现有的有源电磁法理论。

1  均匀大地表面上交变电偶极子的电磁场

如图1所示，在均匀大地表面上敷设长为dL的发送电偶极源，通过它向地下发送电流为I的谐变电流。取x轴沿偶极矩的正向，z轴垂直向下的直角坐标系和1个原点，θ角从0x轴算起的圆柱坐标系，这一场源在观测点处产生的电磁场E_x和H_y分量为^[1-6]：

式中：E_x为与源同向的电场水平分量；H_y为与源布设方向垂直的磁场水平分量；P_E为偶极源的电偶极矩，P_E=IdL；I为供电电流；dL为电偶极源的长度；i为纯虚数；为电偶极源方向和源的中点到接收点矢径之间的夹角；r为收发距，即观测点距偶极子中心的距离；为均匀大地电阻率；，为均匀大地的波数；η为均匀大地导磁率；ε均匀大地介电常数；I₀，I₁，K₀和K₁分别为以为变量的0阶、1阶，第1类、第2类修正贝塞尔函数。

图1  均匀大地表面上水平偶极及坐标示意图

Fig. 1  Sketch map of homogeneous half-space and HED

当＜＜ 1时，电磁场处于近区，式和的渐进表达式为^[2]：

当＞＞ 1时，电磁场处于远区，式和的渐进表达式为^[2]：

从式~可知：在CSAMT方法中，若采用水平电偶极源作为发射源，则近区时，电场水平分量E_x与电阻率成正比，与频率无关，H_y与电阻率无关；E_x按衰减，H_y按衰减，阻抗Z_xy()则按衰减；远区时，E_x与频率无关，与电阻率成正比；H_y与频率有关，与电阻率的平方根成正比；远区时，E_x按衰减，H_y也按衰减。阻抗Z_xy的衰减率与r无关。因此，在远区时，阻抗与收发距无关，与大地电阻率的平方根成正比；近区时，阻抗与几何因素有关；远区时，阻抗与几何因素无关。

2  衰减率的定义

式中：r₂和r₁为收发距；E_x1(H_y1)是收发距为r₁时的场强，E_x2(H_y2)是收发距为r₂时的场强；n_E为E_x的衰减率；n_H为H_y的衰减率；n_Z为阻抗Z的衰减率。若定义n_E，n_H和n_Z分别为水平电场E_x、水平磁场H_y和阻抗Z的衰减系数，则可以求出响应曲线的在双对数坐标系统中的斜率，而这个斜率与场的衰减率对应，如当n_E=-3时，则E_x按r^-3衰减。

3  CSAMT的衰减规律分析及场区划分

3.1  均匀半空间

当电阻率为5 kΩ·m，发射偶极矩为1×10⁷ A·m时，CSAMT的均匀半空间模型轴向装置不同频率的E_x和H_y响应曲线分别如图2和图3所示。图2和图3采用的都是双对数坐标，图2的横坐标为收发距r，图3的横坐标为感应数p。感应数p的计算公式为

图2  轴向模式下均匀半空间E_x和H_y的不同频率场强曲线

Fig. 2  E_x and H_y response curves with different frequencies for axial array

图3  轴向模式下均匀半空间E_x，H_y和阻抗Z_xy的不同频率场强曲线

Fig. 3  E_x, H_y and impedance Z_xy response curves with different frequencies for axial array

从图2可见：当均匀半空间的E_x响应曲线在收发距非常小或非常大时，不同频率的曲线吻合，只是在中等收发距时出现细微差异；当均匀半空间的H_y响应曲线在收发距非常小时，不同频率的曲线吻合，但随着收发距的增大，曲线不再吻合，且场强随着频率的增高而降低。

在双对数坐标系统中，无论是E_x还是H_y，在收发距非常小或非常大(或者可以说是近区或远区)时的响应曲线斜率是固定的，只是在中等收发距(或过渡区)的斜率发生变化。若用感应数来分析(图3)，则无论E_x还是H_y在相同感应数时，响应曲线的斜率一样，不同的是场强的幅值，不同频率的场值只是上下平移，阻抗Z_xy具有同样的规律。

图4所示为计算得到的轴向模式的n_E，n_H和n_Z，其中图4(a)按收发距r成图，图4(b)按“感应数”p成图。从图4(a)可以看出：在小收发距时，E_x以衰减，H_y以衰减，Z_xy以衰减；大收发距时，E_x和H_y均以衰减，但规律较乱，Z_xy的衰减与r无关。若用感应数分析，发现不同频率的n_E，n_H或n_Z曲线完全重合，E_x的衰减率在小感应数为时，随着感应数的增大，衰减率先是增大后减小，再增大、再减小至稳定值，出现3个极值，类似于波浪前进；H_y的衰减率在小感应数为时，随着感应数的增大，衰减率先增大后减小至稳定值，出现1个极值，与E_x相比相对简单；Z_xy的衰减率在小感应数为时，随着感应数的增大，衰减率先是增大后减小，再增大、再减小至稳定值r⁰，这时的Z_xy与r无关，出现3个极值，类似于波浪前进，与E_x的变化规律类似。从场强表达式中可看出Z_xy与E_x衰减规律的相似性，说明E_x相对于H_y对Z_xy的贡献更大。

假设小感应数时，n_E=-3时电场强度E_x进入近区，n_H=-2，n_Z=-1时磁场强度H_y、阻抗Z_xy进入近区，并假定衰减率计算误差为1‰，也就是，，，则E_x的近区范围为0≤p≤0.158，H_y的近区范围为0≤p≤0.073，Z_xy的近区范围为0≤p≤0.055。同理，假设大感应数n_E=-3时电场强度E_x远区，n_H=-3，n_Z=0时磁场强度H_y、阻抗Z_xy进入远区，并假定衰减率计算误差为1‰，也就是，则E_x的远区范围为p≥11.450，H_y的远区范围为p≥6.994，Z_xy的远区范围为p≥12.294。由此可知：E_x的近区范围相对H_y大，即H_y进入过渡区更快；H_y进入远区也更快，Z_xy进入远区最慢。

基于上述分析，在衰减率容许误差为1‰且为轴向模式时， E_x在11.450倍趋肤深度时进入远区，H_y在6.994倍趋肤深度时进入远区，Z_xy在12.294倍趋肤深度时进入远区，H_y较E_x在更小的收发距上进入过渡区，也更早进入远区。

近区时阻抗与几何因素有关，远区时阻抗与几何因素无关。由于电磁波的水平分量处于远区时的衰减率一致，所以，由相互正交的电磁场水平分量定义的阻抗与收发距无关，与大地电阻率的平方根成正比。当电磁波处于近区和远区间的过渡区时，E_x和H_y的衰减率不一致，说明过渡区的阻抗是包含地电信息的。

同理求得赤道模式时的衰减系数，如图5和图6所示。赤道模式的衰减规律与轴向模式有较大区别，E_x的衰减率在小感应数为时，随着感应数的增大， 衰减率先变小后增大，再变小至稳定值，出现3个极值，类似于波浪前进，但不同于轴向模式。H_y的衰减率在小感应数为时，随着感应数的增大，衰减率先变小后增大，后再减小至稳定值，出现2个极值；Z_xy的衰减率在小感应数为时，随着感应数的增大，衰减率先减小再增大至稳定值r⁰，这时Z_xy与r无关，出现1个极值，类似于波浪前进，与E_x和H_y都不同。

图4  轴向模式下均匀半空间E_x，H_y和阻抗Z_xy的衰减曲线

Fig. 4  Attenuate rate of E_x, H_y and impedance Z_xy with different frequencies for axial array

图5  赤道模式下均匀半空间E_x, H_y和阻抗Z_xy(即|E_x/H_y|)的不同频率场强曲线

Fig. 5  E_x, H_y and impedance Z_xy response curve with different frequencies for equatorial array

图6  赤道模式下均匀半空间E_x, H_y 和 阻抗Z_xy(即|E_x/H_y|)的衰减曲线

Fig. 6  Attenuate rate of E_x, H_y and impedance Z_xy with different frequencies for equatorial array

假设小感应数时，n_E=-3时电场强度E_x进入近区，n_H=-2，n_Z=-1时磁场强度H_y、阻抗Z_xy进入近区，并假定衰减率计算误差为1‰，也就是，，，则E_x的近区范围为0≤p≤0.117，H_y的近区范围为0≤p≤0.073，Z_xy的近区范围为0≤p≤0.062。同理，假设大感应数n_E=-3时电场强度E_x进入远区，n_H=-3，n_Z=0时磁场强度H_y、阻抗Z_xy进入远区，并假定衰减率计算误差为1‰，也就是，则E_x的远区范围为p≥9.198，H_y的远区范围为p≥9.924，Z_xy的远区范围为p≥10.915。由此可知：E_x的近区范围比H_y的大，即H_y进入过渡区更快；H_y进入远区也更快，Z_xy进入远区最慢。

基于上述分析，在衰减率容许误差为1‰，轴向模式时， E_x在9.198倍趋肤深度时进入远区，H_y在9.924倍趋肤深度时进入远区，Z_xy在10.915倍趋肤深度时进入远区，H_y较E_x在更大的收发距上进入过渡区，也更早进入远区。

衰减率容许误差为1‰，1%和5%时的区划结果如表1所示。从表1可见：随着衰减率容许误差的增大，区划结果变化较大，如轴向模式中，当衰减率容许误差为1%时，区划结果与1‰的类似，Z_xy在最近的收发距上进入了过渡区，H_y的次之，E_x则在最远的收发距上才进入过渡区；H_y在最小的收发距上进入远区，E_x的次之，Z_xy的远区条件最难满足；当衰减率容许误差为5%时，H_y在最小的感应数上进入远区，E_x的次之，Z_xy的最远。赤道模式中，当衰减率容许误差为1%时，近区的区划结果与衰减率容许误差为1‰，但远区区划结果类似，均是E_x在最小的收发距进入远区，H_y的次之，Z_xy在最大的收发距上进入远区。

轴向模式和赤道模式的远区区划结果有较大差异，衰减率在1‰，1%和5%的误差条件下，轴向模式进入远区的顺序为H_y，E和Z_xy；而赤道模式为E_x，H_y和Z_xy。

3.2  2层模型

为认识地球介质2层断面电磁场的衰减特征，计算2层D和G模型不同频率的E_x和H_y响应曲线。对G型断面，r₁=100Ω·m，r₂=1 kΩ·m，h₁=1 km；对D型断面，r₁=1 kΩ·m，r₂=100Ω·m，h₁=1 km。发射偶极矩为1×10⁴ A·m。

图7和图8所示为2层D型轴线和赤道装置不同频率的E_x和H_y响应曲线，图9和图10所示为2层G型轴线和赤道装置不同频率的E_x和H_y响应曲线。其

中，横坐标均为感应数p₁。感应数p₁的计算公式如下：

分析图7~10可知：无论是D型还是G型地电断面，E_x的响应曲线随着频率的变化，不但数量级不同，曲线形态亦有很大区别，表现在不同收发距(感应数)曲线的斜率不同，差异明显；H_y的响应曲线随着频率的变化表现更明显的是场值数量级的差异，曲线形态高度相似；Z_xy的响应曲线随着频率的改变变化明显，特别是在小感应数处(亦即是近区和过渡区)变化更剧烈。若用衰减率来表示，则E_x，H_y和Z_xy的变化特征更明显，无论是用收发距还是感应数来分析，E_x和Z_xy的衰减率变化最剧烈，也高度相似，H_y的变化幅度小。

表1  均匀半空间E_x,H_y和Z_xy在不同误差条件下进入近区和远区的感应数

Table 1  EM fields division with difference permissible error

图7  轴向模式下D型地电模型E_x, H_y和Z_xy(即|E_x/H_y|)的不同频率场强曲线

Fig. 7  E_x, H_y and Z_xy response curve with different frequencies for axial array

图8  赤道模式下D型地电模型E_x, H_y和Z_xy(即|E_x/H_y|)的不同频率场强曲线

Fig. 8  E_x, H_y and Z_xy response curve with different frequencies for equatorial array

图9  轴向模式下G型地电模型E_x, H_y和阻抗Z_xy(即|E_x/H_y|)的不同频率场强曲线

Fig. 9  E_x, H_y and impedance Z_xy response curve with different frequencies for axial array

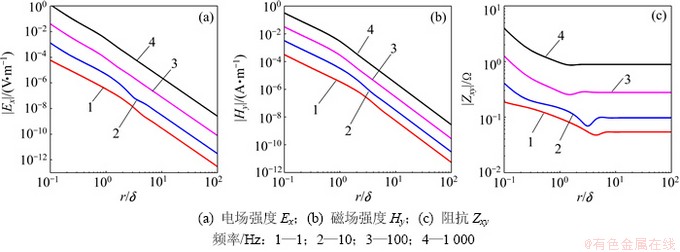
图10  赤道模式下G型地电模型E_x, H_y和阻抗Z_xy(即|E_x/H_y|)的不同频率场强曲线

Fig. 10  E_x, H_y and impedance Z_xy response curve with different frequencies for equatorial array

D型地电断面的E_x在赤道模式时的衰减率变化幅度比轴向模式的大，无论是极小值还是极大值，赤道模式都比轴向模式的大，而H_y反之，Z_xy的情况与E_x一样。这种现象在G型地电模型中也一样。

电磁地球物理探测的目的是基于地下介质的电磁响应，反算地下介质的电性特征、分布情况等。对于同等条件下的同一个目标体，响应越强烈，变化幅度越大，就越有利于探测。就衰减率而言，电场较磁场更强，阻抗Z_xy的响应与电场E_x关系更密切。过渡区的衰减率变化剧烈，包含丰富的地电信息；磁场的变化量变化幅度小，不同模型的变化趋势类似，这也从一个侧面说明磁场的敏感性或分辨率或响应比电场的弱；电场E_x的变化剧烈，且与阻抗Z_xy的变化类似，说明电场E_x与阻抗Z_xy的分辨能力或响应类似。由于H_y的分辨能力较弱，导致电场E_x的分辨能力较阻抗Z_xy更强。

由于2层模型中找不到统一的趋肤深度计算公式，导致基于感应数分析E_x，H_y和Z_xy的衰减率时，情况相对于均匀半空间有很大差异，无法用统一的感应数来进行场区划分。

4  结论

(1) 采用衰减率进行水平电偶极子源的电磁波场区划分，计算分析了均匀半空间和两层模型的轴向和赤道模式E_x，H_y和Z_xy的衰减率，揭示了水平电偶极子源电磁波衰减率随收发距(感应数)的变化规律，并基于均匀半空间E_x，H_y和Z_xy的衰减率进行场区划分，讨论了E_x，H_y和Z_xy衰减率在不同场区的衰减特性。

(2) 轴向模式时，E_x的衰减率在小感应数为时，随着感应数的增大，衰减率先增大后减小、再增大、再减小至稳定值，出现3个极值，类似于波浪前进。H_y的衰减率在小感应数为时，随着感应数的增大，衰减率先是增大后减小至稳定值，出现1个极值，与E_x相比相对简单。

(3) 赤道模式的衰减规律与轴向模式有较大区别。E_x的衰减率在小感应数为时，随着感应数的增大，衰减率先是变小、后增大、再变小，再减小至稳定值，出现3个极值，类似于波浪前进，但不同于轴向模式。H_y的衰减率在小感应数为时，随着感应数的增大，衰减率先变小然后增大，后再减小至稳定值，出现3个极值。

(4) 无论是轴向模式还是赤道模式，过渡区的衰减率变化剧烈，包含有丰富的地电信息；磁场强度的变化幅度小，不同模型的变化趋势类似，说明磁场的分辨率比电场的分辨率小；电场E_x的变化剧烈，且与阻抗Z_xy的类似，说明电场E_x与阻抗Z_xy的分辨能力或响应类似。由于H_y的分辨能力较弱，导致电场E_x的分辨能力较阻抗Z_xy更强。无论是赤道模式还是轴向模式，H_y相对于E_x在更小的距离进入过渡区和远区。

(5) 根据电磁波场的衰减率变化规律，提出了一种新的近区、过渡区和远区的区划方法，丰富了有源电磁法的场区划分方法。

(6) 本文有关场区划分的研究是基于均匀半空间得到的，下一步的工作重点是开展二维和三维数值模拟，以揭示二维和三维条件下的场区划分规律。

参考文献：

[1] 何继善. 广域电磁法和伪随机信号电法[M]. 北京: 高等教育出版社, 2010: 34-88.

HE Jishan. Wide field electromagnetic sounding methods and pseudo-random signal coding electrical method[M]. Beijing: Higher Education Press, 2010: 34-88.

[2] 何继善. 可控源音频大地电磁法[M]. 长沙: 中南工业大学出版社, 1990: 5-30.

HE Jishan. Control source audio-frequency magnetotellurics[M]. Changsha: Central South University of Technology Press, 1990: 5-30.

[3] 汤井田, 何继善. 可控源音频大地电磁法及其应用[M]. 长沙: 中南大学出版社, 2005: 15-60.

TANG Jingtian, HE Jishan. Theory and application of CSAMT method[M]. Changsha: Central South University Press, 2005: 15-60.

[4] 底青云, 王若. 可控源音频大地电磁数据正反演及方法应用[M]. 北京: 科学出版社, 2008: 15-18.

DI Qingyun, WANG Ruo. CSAMT forward modeling and inversion and its application[M]. Beijing: Science Press, 2008: 15-18.

[5] 朴化荣. 电磁测深法原理[M]. 北京: 地质出版社, 1990: 75-100.

PIAO Huarong. The principle of electromagnetic sounding[M]. Beijing: Geological Press, 1990: 75-100.

[6] 石昆法. 可控源音频大地电磁法理论与应用[M]. 北京: 科学出版社, 1999: 16-35.

SHI Kunfang. Theory and application of CSAMT method[M]. Beijing: Science Press, 1999: 16-35.

[7] Zonge K, Hughes L. Controlled source audio-frequency magnetotellurics[J]. Electromagnetic Methods in Applied Geophysics, 1991, 2(Part B): 713-809.

[8] Zonge K L, Ostrander A G, Emer D F. Controlled-source audiofrequency magnetotelluric measurements[C]// Vozoff K. Magnetotelluric Methods. Society of Exploration Geophysicists, 1986: 749-763.

[9] Goldstein M A, Strangway D W. Audio-frequency magnetotellurics with a grounded electric dipole source[J]. Geophysics, 1975, 40(4): 669-683.

[10] Li X, Pedersen L B. Controlled source tensor magnetotellurics[J]. Geophysics, 1991, 56(9): 1456-1461.

[11] Li X, Pedersen L B. Controlled-source tensor magnetotelluric responses of a layered earth with azimuthal anisotropy[J]. Geophysical Journal International, 1992, 111(1): 91-103.

[12] Routh P, Oldenburg D W. Inversion of controlled source audio-frequency magnetotelluric data for a horizontally layered Earth[J]. Geophysics, 1999, 64(6): 1689-1697.

[13] Li X, Oskooi B, Pedersen L B. Inversion of controlled-source tensor magnetotelluric data for a layered earth with azimuthal anisotropy[J]. Geophysics, 2000, 65(2): 452-464.

[14] 刘颖, 柳建新, 何展翔, 等. 频率域双极源全区视电阻率的计算及分析[J]. 地球物理学进展, 2011, 26(2): 675-686.

LIU Ying, LIU Jianxin, HE Zhanxiang, et al. The calculation and analyzing of the bipolar source all time apparent resistivity in frequency domain[J]. Progress in Geophys, 2011, 26(2): 675-686.

[15] 席振铢, 徐培渊, 龙霞, 等. 正交水平磁偶源的电磁场分布规律[J]. 地球物理学报, 2011, 54(6): 1642-1648.

XI Zhenzhu, XU Peiyuan, LONG Xia, et al. The electromagnetic field distribution generated from the orthogonal horizontal magnetic dipole source[J]. Chinese J Geophys, 2011, 54(6): 1642-1648.

[16] 安志国, 底青云, 郭韶华. 隐伏煤矿区 CSAMT 法煤系地层勘查研究[J]. 中国矿业大学学报, 2008, 37(1): 118-124.

AN Zhiguo, DI Qingyun, GUO Shaohua. Study of exploration for coal stratum with CSAMT method in concealed mine area[J]. Journal of China University of Mining & Technology, 2008, 37(1): 118-124.

[17] 王艳, 林君, 周逢道, 等. CSAMT法深部低阻分辨能力及方法研究[J]. 中国矿业大学学报, 2009, 38(1): 86-90.

WANG Yan, LIN Jun, ZHOU Fengdao, et al. Study of resolution and method of CSAMT for the deep low-resistivity[J]. Journal of China University of Mining & Technology, 2009, 38(1): 86-90.

[18] 汤井田, 张林成, 公劲喆, 等. 三维频率域可控源电磁法有限元-无限元结合数值模拟[J]. 中南大学学报(自然科学版), 2014, 45(4): 1252-1260.

TANG Jingtian, ZHANG Lincheng, GONG Jinzhe, et al. 3D frequency domain controlled source electromagnetic numerical modeling with coupled finite-infinite element method[J]. Journal of Central South University (Science and Technology), 2014, 45(4): 1252-1260.

[19] 刘振铎, 刘宝利, 王树青, 等, 磁偶源频率测深法[M]. 北京: 地质出版社, 1985: 3-24.

LIU Zhenduo, LIU Baoli, WANG Shuqing, et al. Frequency sounding with a magnetic dipole[M]. Beijing: Geological Press, 1985: 3-24.

[20] 李帝铨, 底青云, 王妙月. 电离层—空气层—地球介质耦合下大尺度大功率可控源电磁波响应特征研究[J]. 地球物理学报, 2010, 53(2): 411-420.

LI Diquan, DI Qingyun, WANG Miaoyue. Study of large scale large power control source electromagnetic with “earth- ionosphere” mode[J]. Chinese J Geophys, 2010, 53(2): 411-420.

[21] 底青云, 王光杰, 王妙月, 等. 长偶极大功率可控源激励下目标体电性参数的频率响应[J]. 地球物理学报, 2009, 52(1): 275-280.

DI Qingyun, WANG Guangjie, WANG Miaoyue, et al. Frequency response characteristics of target electric property with long bipole large power control source[J]. Chinese J Geophys, 2009, 52(1): 275-280.

[22] 陈小斌, 赵国泽. 关于人工源极低频电磁波发射源的讨论—均匀空间交流点电流源的解[J]. 地球物理学报, 2009, 52(8): 2158-2164.

CHEN Xiaobin, ZHAO Guoze. Study on the transmitting mechanism of CSELF waves: response of the alternating current point source in the uniform space[J]. Chinese J Geophys, 2009, 52(8): 2158-2164.

[23] 底青云, 王妙月, 王若, 等. 长偶极大功率可控源电磁波响应特征研究[J]. 地球物理学报, 2008, 51(6): 1917-1928.

DI Qingyun, WANG Miaoyue, WANG Ruo, et al. Study of the long bipole and large power electromagnetic field[J]. Chinese J Geophy, 2008, 51(6): 1917-1928.

[24] 汤井田, 周聪, 张林成. CSAMT电场y方向视电阻率的定义及研究[J]. 吉林大学学报(地球科学版), 2011, 41(2): 552-558.

TANG Jintian, ZHOU Cong, ZHANG Lincheng. A new apparent resistivity of CSAMT defined by electric field y-direction[J]. Journal of Jilin University (Earth Science Edition), 2011, 41(2): 552-558.

[25] 谢维, 王京彬, 朱谷昌, 等. 线圈中心测量垂直磁场虚分量频域电磁法数值模拟[J]. 中南大学学报(自然科学版), 2013, 44(4): 1444-1452.

XIE Wei, WANG Jingbin, ZHU Gucang, et al. Numerical simulation on frequency domain electromagnetic sounding method of measuring magnetic field vertical imaginary component in center of loop[J]. Journal of Central South University (Science and Technology), 2013, 44(4): 1444-1452

[26] 胡博, 岳建华, 于润桥. 巷道对全空间瞬变电磁场影响的边界元数值模拟[J]. 中国矿业大学学报, 2013, 42(5): 12-19.

HU Bo, YUE Jianhua, YU Runqian. Numerical simulation of the roadway effect on whole-space transient electromagnetic fields by boundary element method[J]. Journal of China University of Mining & Technology, 2013, 42(5): 12-19.

[27] 杨海燕, 岳建华. 吸收边界条件在全空间瞬变电磁计算中的应用[J]. 中国矿业大学学报, 2009, 38(2): 263-268.

YANG Haiyan, YUE Jianhua. Application of absorbing boundary condition in whole-space computation of transient electromagnetic response[J]. Journal of China University of Mining & Technology, 2009, 38(2): 263-268.

[28] 岳建华, 杨海燕. 巷道边界条件下矿井瞬变电磁响应研究[J]. 中国矿业大学学报, 2008, 37(2): 152-156.

YUE Jianhua, YANG Haiyan. Research on response of transient electromagnetic field in underground mine with boundary condition of laneway[J]. Journal of China University of Mining & Technology, 2008, 37(2): 152-156.

(编辑  陈灿华)

收稿日期：2013-10-05；修回日期：2013-12-20

基金项目：国家自然科学基金资助项目(41204054)；中国博士后科学基金资助项目(20110490149)；湖南科技大学页岩气资源利用省重点实验室开发基金资助项目(E21423)

通信作者：李帝铨(1982-)，男，广西玉林人，博士，从事电磁法研究；电话：15802637512；E-mail: lidiquan@csu.edu.cn