航空铝合金薄壁件铣削加工变形的预测模型
王光宇,吴运新,闫鹏飞,胡永会
(中南大学 机电工程学院,湖南 长沙,410083)
摘要:为预测航空铝合金薄壁件的铣削加工变形,建立三维有限元模型。通过有限元软件MSC.MARC,向有限元模型添加初始应力场、对节点施加铣削力、控制铣刀路径和对模型的网格进行自适应网格细化。使用该模型进行薄壁零件的铣削仿真。仿真结果表明:铣削之后,薄壁零件呈中间凹陷、四周翘起的盆形。同时,零件的薄壁向内部凹陷。为检验仿真结果的正确性,设计验证实验以测量加工后零件的变形。实验的结果与仿真结果相吻合,证明本文提出的有限元模型可有效预测航空铝合金薄壁件的加工变形。该有限元模型可用来选择合适的加工策略以减小航空铝合金薄壁件的加工变形。
关键词:铝合金;薄壁零件;子程序;铣削加工;有限元模型
中图分类号:TG501;V261 文献标志码:A 文章编号:1672-7207(2012)05-1696-07
Prediction model for machining deformation of aeronautical aluminum alloy thin-walled workpiece
WANG Guang-yu, WU Yun-xin, YAN Peng-fei, HU Yong-hui
(School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China)
Abstract: In order to predict machining deformation of aeronautical thin-walled workpiece, a three-dimensional finite element model was built. By use of finite element software MSC.MARC, the initial stress to the model was added, milling force on nodes was imposed, tool path was controlled and adaptive mesh refinement (AMR) method to the model was developed for the model. Milling simulation of aeronautical thin-walled workpiece was conducted by use of the model. Simulation result shows that after machining, the workpiece presents the shape of basin, which means that the central region of the workpiece is concave and lower than the peripheral region around. In addition, the thin walls are dented toward inside of the workpiece. To test the validity of the simulation results, a verification experiment to measure the deformation of machined workpiece was conducted. The experimental result coincides with simulation result. It is proved that the proposed finite element model can effectively predict machining deformation of aeronautical aluminum alloy thin-walled workpiece. The proposed finite element model can be applied to select appropriate machining strategies to reduce machining deformation of aeronautical aluminum alloy thin-walled workpiece.
Key words: aluminum alloy; thin-walled workpiece; subroutine; milling; finite element model
随着现代航空工业的发展,在飞机零部件中广泛使用具有复杂结构的薄壁件,如整体框﹑整体梁和整体壁板等。这类零件的共同特点是尺寸大﹑结构复杂、薄壁和精度要求高。由于这类零件的薄壁特性,极易在加工过程中产生翘曲变形。翘曲变形主要由初始残余应力的释放﹑零件结构的不对称和加工工艺的缺陷引起。有时,零件的翘曲变形甚至超过装配许可的误差范围。为此,有时不得不在零件加工完成之后增加校正程序。这不仅降低生产率,而且增加零件的废品率,给制造商和零件的使用者带来巨大的经济损 失[1-3]。为分析加工变形的机理并提出合适的策略以控制加工变形,研究人员进行了相关的仿真和实验。He等[4]将有限元方法用于分析和选择薄壁件加工变形的控制策略。Ratchev等[5]研究薄壁件铣削加工时的误差补偿策略。Weinert等[6-8]将有限元方法用于铝合金结构加工过程的计算分析和薄壁件周铣过程中静态误差的预测。Li等[9]建立端铣仿真模型。Rai等[10]提出加工仿真包以分析加工变形的根本原因和选择合适的加工策略。虽然这些有限元模型考虑铣削力的作用,但该有限元模型在仿真过程中不能进行网格自适应细化,因此该模型不适合大尺寸薄壁件的铣削仿真。Liu等[11-14]研究夹具—工件的完整模型以补偿变形误差和进行夹具的优化设计。Zaghbani等[15]研究铝合金高速干铣过程的力—温度模型以及相关的本构模型。但是它只是一个数学模型,不适合用于预测加工变形。Guo等[16]建立用于预测航空铝合金薄壁件铣削变形的有限元模型,但在仿真过程中,该有限元模型的网格无法进行自适应细化,因此,为获得高精度的仿真结果,必须把网格细分,这导致在进行大尺寸薄壁件的铣削仿真时计算成本较高。本文的目的在于建立同时考虑仿真结果的精度和计算成本的三维铣削加工模型,应用自适应网格细化(AMR)技术,并考虑铣削力对薄壁件的加工变形的影响。AMR技术同时保证加工变形的有效预测和较低的计算成本。在仿真过程中,位于铣刀附近的有限元网格将被细化。考虑铣削力影响的模型,与未考虑铣削力影响的模型相比,其仿真结果更加准确。
1 铣削加工的有限元模型
1.1 有限元模型的网格划分
用于铣削的7075铝合金厚板的尺寸为(长×宽×厚)155 mm×155 mm×40 mm。通过铣削,在该厚板上挖去尺寸为145 mm×145 mm×20 mm的方形块,留下四周壁厚为5 mm、底部厚度20 mm的薄壁零件。
选用六面体单元对模型进行网格划分,使用刚性面模拟夹具。为模拟真实的零件铣削过程,在划分网格之前,通过铣刀直径、铣削宽度、铣削深度和进给速度等多个参数确定六面体单元的尺寸。图1给出铣削前和铣削后的零件有限元模型。
仿真过程中,零件由刚性面固定。通过静态应变仪测得夹具的夹持应力约为20 MPa。将夹持力作为边界条件加入有限元模型中。

图1 铣削前和铣削后的零件的有限元模型
Fig.1 Comparison of finite element models before and after milling
1.2 材料模型
由于铣削过程中使用冷却油,因此,切削热对7075铝合金材料属性的影响未被考虑。另外,考虑到铣削过程中产生的大应变、高应变率等现象集中在刀具切削刃附近的局部区域,不会对零件的整体变形产生影响,因此,大应变和高应变率对7075铝合金的本构关系的影响未被考虑。本文中的有限元模型采用的材料模型为弹塑性材料模型。
1.3 初始残余应力场的施加
文献[17-18]显示,在多种影响薄壁件的最终变形的因素中,零件内部的初始非均匀应力场的影响是最大的。随着铣削的进行,工件的材料被不断去除,从而导致初始应力场在剩余的工件材料内不断地重新分布,从而导致工件发生翘曲和弯扭。这就是初始残余应力场引起零件加工变形的机理。
层削法是一种目前常用的用于测量铝合金厚板内应力的方法[19]。本文使用层削法测量尺寸(长×宽×厚)为155 mm×155 mm×40 mm的7075铝合金厚板的内应力分布。
当没有任何外在载荷作用时,零件的内应力场应该是自平衡的,即工件内任意截面内的合力和合力矩应满足:
 (1)
(1)
 (2)
(2)
其中: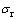 为残余应力;M为力矩;A为截面积。
为残余应力;M为力矩;A为截面积。
为满足式(1)和(2),将测得的厚板轧向和横向沿厚度方向分布的残余应力曲线进行了离散和自平衡处理,得到用于有限元模型的残余应力曲线。图2所示为经离散和自平衡处理后的残余应力曲线。为将离散和自平衡之后的残余应力数据添加到有限元模型中,编制了MARC子程序。该子程序的功能是根据每个单元的空间位置将初始残余应力数据添加到模型的所有单元中。
1.4 铣削力的施加
对薄壁件进行铣削加工时,铣削力对零件变形的影响不可忽略。在铣削过程中,由于铣削力的挤压作用,切削刃附近的局部区域将产生大应变﹑高应变率等现象。由于大应变﹑高应变率等现象的产生过程十分复杂,因此,在仿真中完全模拟这些现象的产生几乎是不可能的。基于此,本文对铣削力的产生和施加过程进行了一定程度的简化。
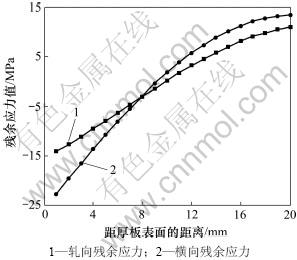
图2 离散和自平衡处理后的厚板内应力曲线
Fig.2 Discretized and self-balanced curve of internal stress of thick plate
真实铣削过程中铣刀的运动是由2种运动合成的:一种是铣刀绕自身的轴线旋转,另一种是铣刀的进给运动。这2种运动的叠加使得铣刀铣削刃的运动轨迹成为1条摆线。铣削刃的这种运动方式导致铣削层的厚度是非均匀变化的。在真实铣削过程中,铣削力的大小与铣削层的厚度有关。因此,以铣刀旋转1周所需的时间为周期,在这个周期内,铣刀的铣削刃微段产生的铣削力是非均匀变化的,即铣削力将随着铣削刃微段的位置的变化而变化。而铣刀产生的总体铣削力则呈周期变化。
直接模拟铣削刃绕自身轴线的旋转和铣刀的进给运动是困难的。为此,将铣刀的运动进行简化。图3显示真实的铣削刃运动轨迹与简化后的铣削刃运动轨迹的对比。简化后,认为铣削刃在1个分析步中的运动是1条直线。但是同时,在仿真中,不同位置的铣削刃微段产生不同大小的铣削力。
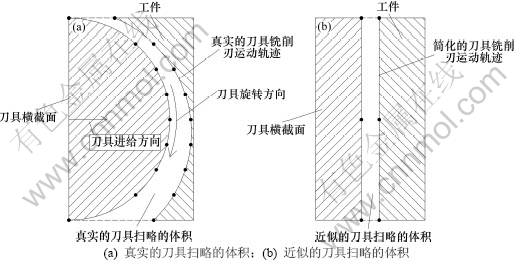
图3 真实的与简化后的铣削力模型的对比
Fig.3 Comparison of real and simplified model of milling force
通过MSC.MARC的子程序接口,按照上述方法向位于模型铣削层的节点施加3个方向(X,Y和Z方向)的铣削力。根据静力等效原则,使铣削层上所有节点的铣削力之和等于铣刀产生的总体铣削力,同时,根据节点的位置对节点施加不同大小的铣削力,如图4所示。通过这种方法,近似地模拟了铣削层厚度的变化对铣削力的影响。
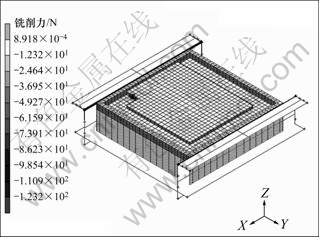
图4 铣削层中各节点的X向铣削力
Fig.4 X-direction milling force applied to nodes
1.5 材料去除和自适应网格细化方法
通过使用生死单元技术,可方便地模拟铣削加工中材料的去除过程。生死单元技术是一种数值方法,它是指在有限元程序中,将有限元方程的刚度矩阵乘以一个非常小的减缩因数(约为10-6),使某个单元失效,从而模拟该单元的“死亡”[3]。
为模拟真实铣削过程中零件材料被逐步去除的过程,编写控制铣刀路径的子程序。在铣削仿真过程中,位于铣刀轴半径范围之内的单元将随着铣刀的运动被杀死。
对大尺寸薄壁件来说,模拟它们的铣削过程是困难的,因为高精度的仿真结果往往需要精细的网格。但是,精细的网格将增加计算成本。为解决这一问题,刘东等[20]利用零件结构的对称性,建立一个大尺寸航空铝合金件的四分之一模型。然而,这种方法对结构不对称的零件来说是不可行的。为同时获得较高的仿真精度和较低的计算成本,本文通过编制相应的子程序,在有限元模型中实现了网格自适应细化。通过使用该子程序,位于铣刀周围的1个方盒内的网格将被细化。该方盒的位置由铣刀的位置决定。图5所示为细化后的模型的局部网格。

图5 细化后的模型的网格(局部图)
Fig.5 Refined mesh of finite element model (local)
2 铣削仿真与实验
2.1 厚板的制备
用于铣削加工实验的厚板是从尺寸(长×宽×厚)为1 200 mm×220 mm×40 mm的7075铝合金厚板上用线切割机切下来的。铝合金厚板的热处理工艺为:在480 ℃保温2 h,于20 ℃水浴淬火。室温为20 ℃。水浴淬火后,将该铝合金厚板进行预拉伸处理,拉伸量为2%。然后,从预拉伸之后的铝合金厚板上切割出相邻2块尺寸(长×宽×厚)为155 mm×155 mm×40 mm的方形厚板。其中一块用于测量原铝合金厚板的内应力分布,另一块用于铣削实验。
2.2 铣削实验及仿真
本文采用d 20三刃螺旋铣刀进行铣削实验。其他铣削参数如下:主轴转速为1 000 r/min,铣削宽度为10 mm,铣削深度为4 mm,总铣削深度为20 mm,进给速度380 mm/min。铣削总共分6步进行,前5步为粗铣,最后1步精铣,精铣余量为0.5 mm。
根据文献[21]的研究,在其他加工条件不变的情况下,走刀路径的选择对零件的加工变形量有较大的影响。其中,外环铣削与并行铣削、“之”字形铣削、内环铣削相比产生的加工变形量较小。图6中的第3种铣削方式即为外环铣削。本文即采用外环铣削方法进行实验和仿真。
3 仿真结果及验证实验
按铣削实验进行时的条件进行仿真计算。铣削仿真完成之后,松开夹具,释放工件。
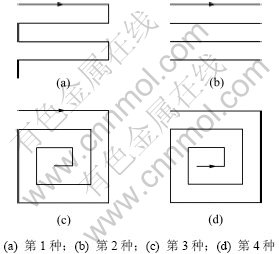
图6 4种铣削路径
Fig.6 Four types of tool paths
图7显示铣削加工之后的零件的变形情况,图中零件的变形放大了400倍。从图7可见:加工后,工件总体呈中间凹陷,四周翘起的形状,同时,工件四周的薄壁向内凹陷。
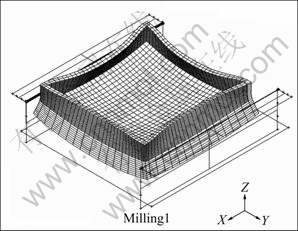
图7 放大之后的零件变形情况
Fig.7 Amplified final deformation of workpiece
3.1 验证实验的测量位置的选择
为验证仿真结果的正确性,需要设计验证实验以测量加工后的零件的变形。
由于零件的下表面相对粗糙,而工件的变形量很小,因此加工后的零件底面的变形量很难直接测量。然而,零件的已加工表面很光滑,适合进行精密的测量。基于上述分析,决定对沿着零件的薄壁的线的垂直方向上的变形量进行测量。图8显示4条线的位置,图中X代表轧向,Y代表横向。
这4条线的变形的仿真结果对比如图9所示。由图9可见:线2和线4在垂直方向(即Z方向)上的变形量相对线1和线3较大,因此,线2和线4更适合用来测量零件的变形量。基于上述分析,使用3坐标测量机GLOBAL STATUS对线4在垂直方向(即Z向)上的变形量进行测量。

图8 4条线的位置
Fig.8 Locations of four lines

图9 4条线的变形量的对比
Fig.9 Comparison of deformation of four lines
3.2 验证实验的结果与仿真结果的对比
为便于比较,对验证实验得到的数据和相应的仿真数据进行了坐标变换处理,以便它们能在同一坐标系下进行对比。图10所示为实验结果与仿真结果的对比。从图10可以看出:尽管仿真结果与实验结果相比还存在着一定的误差,但二者的变化趋势较吻合,都呈开口向上的抛物线形状。
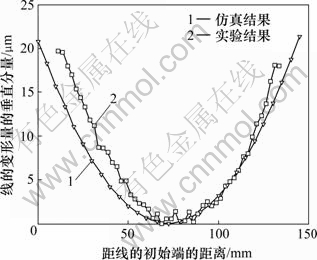
图10 仿真结果与实验结果的对比
Fig.10 Comparison of simulation and experimental result
4 结论
(1) 通过进行铣削仿真与验证实验,证明有限元方法可以有效地预测铝合金薄壁零件的加工变形。有限元仿真结果的可靠性被实验结果所证实,证明有限元模型的预测结果正确。
(2) 本文所提出的有限元模型可以用于选择合适的加工策略以减小航空铝合金薄壁件的加工变形。
参考文献:
[1] 毕运波, 柯映林, 董辉跃. 航空铝合金薄壁件加工变形的有限元仿真与分析[J]. 浙江大学学报: 工学版, 2008, 42(3): 397-402.
BI Yun-bo, KE Ying-lin, DONG Hui-yue. Finite element simulation and analysis of deformation in machining of aeronautical aluminum alloy thin-walled workpiece[J]. Journal of Zhejiang University: Engineering Science, 2008, 42(3): 397-402.
[2] 成群林, 柯映林, 董辉跃. 航空铝合金高速铣削加工的有限元模拟[J]. 浙江大学学报: 工学版, 2006, 40(1): 113-117.
CHENG Qun-lin, KE Ying-lin, DONG Hui-yue. Simulation of high-speed milling process of aerospace aluminum alloy[J]. Journal of Zhejiang University: Engineering Science, 2006, 40(1): 113-117.
[3] 成群林, 柯映林, 董辉跃, 等. 航空整体结构件铣削加工变形预测研究[J]. 浙江大学学报: 工学版, 2007, 41(5): 799-803.
CHENG Qun-lin, KE Ying-lin, DONG Hui-yue, et al. Distortion prediction for milling process of aerospace monolithic components[J]. Journal of Zhejiang University: Engineering Science, 2007, 41(5): 799-803.
[4] HE Ning, WANG Zhi-gang, JIANG Cheng-yu, et al. Finite element method analysis and control stratagem for machining deformation of thin-walled components[J]. Journal of Materials Processing Technology, 2003, 139: 332-336.
[5] Ratchev S, Liu S, Becker A A. Error compensation strategy in milling flexible thin-wall parts [J]. Journal of Material Processing Technology, 2005, 162/163: 673-681.
[6] Weinert K, Biermann D, Kersting M, et al. Experimental and computational analysis of machining processes for light-weight aluminum structures[J]. Advanced Materials Research, 2008, 43: 97-104.
[7] Weinert K, Grunert S, Kersting M. Analysis of cutting technologies for lightweight frame components in flexible manufacture of lightweight frame structures[J]. Advanced Materials Research, 2006, 10: 121-132.
[8] Wan M, Zhang W H, Qiu K P, et al. Numerical prediction of static for errors in peripheral milling of thin-walled workpieces with irregular meshes[J]. Journal of Manufacturing Science and Engineering, 2005, 127(1): 13-22.
[9] LI Hong-qi, SHIN Y C. A comprehensive dynamic end milling simulation model[J]. Journal of Manufacturing Science and Engineering, 2006, 128(1): 86-95.
[10] Rai J K, Xirouchakis P. Finite element method based machining simulation environment for analyzing part errors induced during milling of thin-walled components[J]. Internal Journal of Machine Tools & Manufacture, 2008, 48(6): 629-643.
[11] Liu S, Zheng L, Zhang Z H, et al. Optimal fixture design in peripheral milling of thin walled workpieces[J]. International Journal of Advanced Manufacturing Technology, 2006, 28(7): 653-658.
[12] Satyanarayana S, Melkote S N. Finite element modeling of fixture–workpiece contacts: single contact modeling and experimental verification[J]. International Journal of Machine Tool and Manufacture, 2004, 44(9): 903-913.
[13] Sanchez H T, Estrems M, Faura F. Analysis and compensation of positional and deformation errors using integrated fixturing analysis in flexible machining parts[J]. International Journal of Advanced Manufacturing Technology, 2006, 29(3): 239-252.
[14] Liao Y G, Hu S J. An integrated model of a fixture–workpiece system for surface quality prediction[J]. International Journal of Advanced Manufacturing Technology, 2001, 17(11): 810-818.
[15] Zaghbani I, Songmene V. A force-temperature model including a constitutive law for dry high speed milling of aluminum alloys[J]. Journal of Materials Processing Technology, 2009, 209(5): 2532-2544.
[16] Guo H, Zuo D W, Wu H B, et al. Prediction on milling distortion for aero-multi-frame parts[J]. Materials Science and Engineering A, 2009, 499(1): 230-233.
[17] 孙杰, 柯映林, 吴群, 等. 大型整体结构件数控加工变形校正的关键技术研究[J]. 机械工程学报, 2003, 39(8): 120-124.
SUN Jie, KE Ying-lin, WU Qun, et al. Study on key technologies of straightening large-scale integrated part distortion due to machining[J]. Chinese Journal of Mechanical Engineering, 2003, 39(8): 120-124.
[18] Denkena B, Leon L D. Milling induced residual stresses in structural parts out of forged aluminum alloys[J]. International Journal of Machining and Machinability of Materials, 2008, 4(4): 335-344.
[19] LIAO Kai, WUW Yun-xin, GONG Hai. Pre-stretching simulation and residual stresses measurement in aluminum alloy thick plates[C]//2009 International Conference on Measuring Technology and Measurement Automation, 2009: 287-291.
[20] 刘东, 陈五一. 大型薄壁整体结构件加工变形仿真, 2008, 20(6): 1589-1593.
LIU Dong, CHEN Wu-yi. Simulation of thin wall integral structure distortion during machining[J]. Journal of System Simulation, 2008, 20(6): 1589-1593.
[21] GUO Hun, ZUO Dun-wen, WANG Shu-hong, et al. Effect of tool-path on milling accuracy under clamp-ping[J]. Transactions of NUAA, 2005, 22(3): 234-239.
(编辑 邓履翔)
收稿日期:2011-05-03;修回日期:2011-08-26
基金项目:国家重点基础研究发展计划(“973”计划)项目(2010CB731703)
通信作者:吴运新(1963-),男,广东兴宁人,教授,博士生导师,从事有限元仿真,铝合金机加工研究;电话: 0731-88830813;E-mail: wuyunxin@csu.edu.cn