文章编号：1004-0609(2010)07-1424-09

喷淋液流速率与气流速率对次生硫化铜矿

生物堆浸过程温度分布的影响

李宏煦¹，李  安¹，吴爱祥²，邱冠周³

(1. 北京科技大学 冶金与生态工程学院，北京 100083；

2. 北京科技大学 土木与环境工程学院，北京 100083；

3. 中南大学 资源加工与生物工程学院，长沙 410083)

摘  要：在假定辉铜矿、黄铁矿生物氧化反应步骤和反应产热一定的情况下，基于反应热的计算及热力学基本理论，建立生物堆浸过程热平衡方程，研究堆浸过程反应产热、喷淋液流速率和充气气流速率对堆中温度变化及分布的影响。仿真结果显示；堆中温度的分布及变化与喷淋液流速率(G_l)、气流速率(G_a)直接相关，且与G_a/G_l有密切关系；若喷淋液流速率G_l过大，堆中热量积聚于堆的底部；若气流速度过大，则热量通过对流上升到堆的顶部；若两种流速过大均会使热量通过底部和顶部的蒸发而损失，确定合理的G_a/G_l是实现堆中温度理想分布的途径；当G_a/G_l为2/3时，堆中温度分布较好。

关键词：次生硫化铜矿；生物浸出；生物堆浸；热平衡；温度场

中图分类号：TF111.31；TF803.21　　     文献标志码：A

Effect of irrigation rate and air flow rate on temperature distribution of secondary copper sulfide during bio-heap leaching process

LI Hong-xu¹, LI An¹, WU Ai-xiang², QIU Guan-zhou³

 (1. School of Metallurgical and Ecological Engineering, University of Science and Technology, Beijing 100083, China;

2. School of Civil and Environment, University of Science and Technology, Beijing 100083, China;

3. School of Minerals Processing and Bioengineering, Central South University, Changsha 410083, China)

Abstract: By assuming that the step and heat of the bio-oxidation reaction of chalcocite and pyrite are definite, based on the calculation of the heat of reaction, the heat balance equation of the bio-heap leaching process was established. The effects of the heat produced, the irrigation rate and air flow rate on the temperature variation and distribution were investigated. The simulation results show that the heat distribution and variation in the heap are determined by the irrigation rate and air flow rate, especially of their ratio value. When the irrigation rate over increases, the major heat would be brought to and accumulated at the bottom of the heap, conversely if the air flow rate over increases, the major heat would be accumulated at the top of the heap, both of the overlarge rate will cause heat loss from bottom or top of the heap. The determined reasonable ratio of the air flow rate to irrigation rate is an effective way to implement the ideal heat distribution in the heap. The optimized G_a/G_l is 2/3 for better temperature distribution.

Key words: secondary copper sulfide; bioleaching; bio-heap leaching; heat balance; temperature field

堆浸是实现生物提铜冶金的主要方法，尽管次生硫化铜矿生物堆浸已经工业化，从国内外应用情况来看，仍然存在后期浸出速率过慢、浸出率往往低于预期值等问题，其原因在于对生物堆浸过程的许多问题尚不清楚^[1-4]。目前，国内外关于生物冶金研究主要集中在浸矿微生物的选育与培养、微生物生长动力学、生物与矿物相互作用机理等方面，但对实际堆浸过程的研究相对较少，关于堆浸过程动力学的研究鲜有报道。生物堆浸过程影响因素很多，包括微生物的生长代谢，生物与矿物的相互作用，堆中矿物的氧化分解，堆中气体、液体的流动与分布，堆中热平衡和热分布等生物、化学、物理因素，情况复杂。要提高堆浸速率与效率，必须掌握堆浸过程诸多因素影响的规律^[5-12]。本文作者在冶金热力学基础上对次生硫化铜矿生物堆浸过程堆中温度的分布进行仿真，考查堆中浸出液流速和气体流速对堆浸过程堆中温度的影响，讨论堆中温度的主要控制因素，定量认识堆浸过程的机理，以期优化堆浸过程。

1  堆浸过程热平衡模型及边界条件的确立

1.1  反应的离子热

假定微生物在堆中仅产生间接作用，堆中生物氧化浸出反应为稳态过程；堆中包括三相，由固体矿物和静态溶液组成的停滞相；液相由上向下流动，气相由下向上流动。堆内任一深度上三相均达到热平衡；堆中任一点的气相均渗透在水蒸气相中；堆中任意点的物理和热力学参数性质一致； 氧化物溶解过程既没有热产生也没有热消耗；硫酸盐的沉淀过程亦既没有热产生也没有热消耗；每摩尔电子转移均产生100 kJ的热量；所有的亚铁离子均被氧化为高铁^[12-14]。在假定特定条件下的反应产热为一恒定值，根据堆中硫化矿反应热焓的计算结果，计算出等摩尔反应离子的产热，结果列于表1中。

表1  反应的离子热

Table 1  Produced heat value of reactive ion

1.2  堆中热平衡模型

可以认为堆中基本的热平衡为^[15-22]堆中热积聚速度是传导热净输入速率、对流热净输入速率、反应净产热速率之和。

假设在堆中任一深x处的所有相的热保持平衡，那么通过厚度(h)和面积A单元的热平衡可表示为

   (1)

式中：ρ为堆平均密度； q为传导热；h为表面热传递系数；mh为对流热；下标l，a 和v分别表示液流、干空气和水蒸气；S为堆中单位体积中化学反应的放出热；x为单位长度。将式(1)对AΔx微分，可认为Δx趋向于零，第一步微分导出热平衡式：

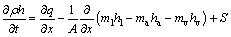        (2)

根据Fourier传导定律

                                  (3)

式中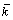：为堆平均热传导率；T为温度。将式(3)代入式(2)可得：

            (4)

假定在堆中没有水的净累积，渗流过程气体饱和湿度为水蒸气对干空气物质比，则有：

                      (5)

式中：ψ为饱和湿度；p_v(T)为蒸汽压力。于是水的稳态平衡可表示为

                          (6)

对式(6)积分，可得液体水的物质传递速率为

            (7)

将式(7)代入式(4)可得：

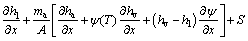      (8)

根据各个比热容，则各热焓为

式中：d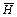为平均热；dH_l为液体热；dH_a为气体热；dH_v为蒸发热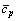；为平均定压比热容；c_pl为液体的定压比热容；c_pa为干空气的定压比热容；c_pv为水蒸气的定压比热容。蒸发潜热为

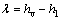                                  (9)

在考虑堆表面蒸发水的损失量下，喷淋液体和空气的物质流量如下：

       (10)

式中：G_l为液体流量，即堆喷淋流流速率；G_a为气流速率，即堆中气体流速；k_g为气体热传导率；ρ_g为气体密度；ω_∞为大气环境湿度。

综上所述，在考虑液体、气体流动和蒸发时堆的热分布变化可表示为

        (11)

式中：λψ′为与温度相关的初始湿度的初步微分。 式(11)的边界及初始条件如下。

边界条件BC1：

            (12)

边界条件BC2：

                 (13)

初始条件IC：

                               (14)

式中：ω_a为进入堆中的气体湿度；X为堆高。

边界条件BC1和BC2分别代表通过堆顶部和底部表面热平衡。式(12)左边项代表边界传导热，右边第一项代表堆上部表面和环境接触时的净收入，第二项则代表喷淋液的热贡献。BC2则代表空气和水蒸气蒸发热的净损失。BC1与环境相关的边界热流动由如下几部分组成：

                          (15)

其中：

                           (16)

               (17)

           (18)

式中：α_s为堆表面阳光吸收率；为堆表面灰体辐射率；F_1-2为堆相对天空表观因子。

传导和蒸发热传递可用通过牛顿定律确定，当作为堆表面流体与风速函数的热传递系数h已知时，则物质传递系数k_g可通过Chilton–Colburn近似方程确定：

                (19)

式中：Le为Lewis数。

辐射热包括太阳辐射和灰体与大气的热交换。灰体与大气的热交换在晚上时为净损失；而太阳辐射强度是与辐射角有关的函数：

                (20)

其中，

              (21)

式中：G(Z)为太阳辐射强度；G₀是太阳辐射常数，为1 390 W/m²；t_a为空气衰减因子；l、d、a分别为纬度、倾斜度、太阳光吸收率(太阳随时间变化角度)。

周围大气温度T_∞和有效天空黑体温度T_sky均是与辐射角有关的函数，且在太阳落下时为保持最小值的常数。周围大气温度可表示如下：

(22)

对于天空有效黑体，其温度表示为

  (23)

式中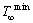：为最小环境温度；为最大环境温度。

以时间形式整理微分热平衡系数，将主要的变量、定义为

令热传导、液相对流、气相对流分别为

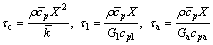
则总热平衡可为

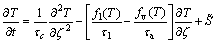          (24)

式中：

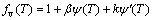
边界条件BC1：

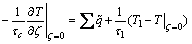             (25)

边界条件BC2：

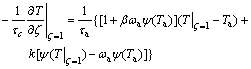     (26)

初始条件IC：

                               (27)

式中：f_l(T)代表堆表面蒸发热损失和堆内与液流方向相反的水蒸气产生的液体薄膜所带热；f_v(T)则代表水蒸气存在下气相热净收入。

热平衡方程可应用有限差分公式进行数学求解，采用专业软件CFD计算。包括传导与对流两中间项和前累积差分项。只要热传导的值足够高，数值解的结果可认为是可靠和严格的。边界条件采用表2中经典热力学数据和现场实际数据确定^[18-22]。

1.3  边界条件的选择

各热力学参数按照标准态和紫金山生物堆浸过程而确定，在整个仿真过程中，假设堆中反应产热S为一恒定常数，并可用初始值S₀替代。随着硫化矿物的氧化，在浸出后期反应放热速率逐步下降，故上述假设认为该变化相对其它因素影响较小，且在浸出的前两个月内，反应基本保持稳态放热，且在随后的时间内，反应放热的下降趋势亦不十分明显。因严格得出硫化矿氧化放热与温度的函数关系较为困难，故在一定精度下假设其不会影响彷真结果。

表2  生物堆浸的热平衡与温度场彷真所选用的参数

Table 2  Practical termal balance data and other selected thermal parameter values for bio-heap leaching

由于相对空气的气压较低和表面环境的复杂性，确定表面导热系数h较为困难，一般取经验值为20 W/(m²?h)。考虑到h的微小变化对堆表面蒸发和热损失产生较大影响，堆的操作过程中，尽量可能采用有效措施来降低表面蒸发。其措施主要有：以滴淋代替喷淋，将滴淋管的一部分埋在堆表面矿石下，甚至在堆表面采用加盖。

2  气体与液体流速对堆中温度分布影响的仿真结果

2.1  堆内平均温度随时间的变化

堆中溶液流速、气流和反应产热速率对堆平均温度变化有较大影响。堆中平均温度可认为是如下式的积分：

               (28)

计算堆内平均温度时，假设1a的浸出率达到80%，硫化矿中硫全部转化为硫酸盐，氧化放热率S₀=20 W/m³。在所取的空气流速G_a一定时，计算相应不同喷淋速率下的堆内平均温度的变化。需要说明的是，尽管所取的空气流速较小，但仍较实际操作中堆中气体流速大，此时氧气的利用率仅约为20%。

图1所示为喷淋速率在G_l=4 kg/(m²?h)时堆平均温度与时间的关系。由图1可知：在该喷淋速率下，在浸出初期，温度上升缓慢，在20 d以后，堆中温度开始加速上升，之后再过10 d后，即浸出时间大约30 d后，温度基本不再上升，这是由于在浸出20~30 d时，大量硫化矿尤其是黄铁矿氧化放出热量。此时可以看出，气流速度越慢，则堆中温度上升越快，当G_a=0.5 kg/(m²?h)时，温度上升最快，达到近90 ℃，但由于供氧速率较慢，温度上升速率较G_a=1.0 kg/(m²?h)、1.5 kg/(m²?h)时的慢；当G_a在2.0 kg/(m²?h)以上时，堆中平均气温最高点较低，在G_a=3.0 kg/(m²?h) 时，堆内最高平均温度仅比初始温度高10 ℃左右，可见，在喷淋液流速率较低情况下，气流速率是决定堆中温度的主要因素之一，气流速度上升会通过对流作用带走堆中热量。

图1  喷淋液流速率G_l=4 kg/(m²?h)时堆平均温度随时间的变化

Fig.1  Variations of heap average temperature with bio- leaching time at irrigation rate of 4 kg/(m²?h)

图2所示为G_l=6 kg/(m²?h)时堆内平均温度随时间的变化关系。由图2可知，在该喷淋速率下，堆中平均温度随时间变化趋势及堆中温度随堆高分布特点与G_l=4 kg/(m²?h)时基本相同，堆中平均气温在20~30 d时上升加快，且自顶部0~6 m处，温度分布趋于平缓。其区别在于，在相同气流速率下堆中的平均温度及堆中最高温度较G_l=4 kg/(m²?h)时的高。这说明在较小的喷淋液流速率范围内，喷淋液流速率的增加会使堆中的平均温度有所上升，这是由于气流速度不变时，喷淋液流速率略微上升使更多的反应剂到达目的矿物，因而反应速率有所提升，单位时间内放出的热量增加，从而堆内温度上升。可见，在喷淋液流速率绝对值较小情况下，适当提高喷淋速率有利于加快反应速率和提高堆中温度。

图3所示为G_l=8 kg/(m²?h)时堆内平均温度随时间的变化关系。与喷淋速率G_l为4、6 kg/(m²?h)时相比，气体流速为2.0和3.0 kg/(m²?h)时，温度均较前二者高，说明在该气流速率下，提高喷淋速率会提高堆中平均温度。与G_l为4和6 kg/(m²?h)不同的是，当G_l一定时，堆中平均温度不再完全随G_a的提高而降低，G_a=1.0 kg/(m²?h)时平均温度最高时仅40 ℃，比G_a=5.0 kg/(m²?h)时还低。说明在该喷淋速率下，气流速率已相对过低，即堆中气体供给不足，反应速率下降。

图4所示为G_l=10 kg/(m²?h)时，堆内平均温度随时间的变化关系。与G_l=8 kg/(m²?h)时表现出的趋势相同，堆中平均温度变化并不随气体流速的增加而一概下降，而是当气体流速在一定范围内变化时，即G_a在6.0、5.0、4.0、3.0 kg/(m²?h)时堆内温度随气流速率的增加呈下降趋势，同样出现G_a=2.0 kg/(m²?h)时堆平均温度比G_a=6.0 kg/(m²?h)时还要低的情况，说明在G_l=10 kg/(m²?h)时气体流速过低也会使堆中的平均温度下降。

图2  喷淋液体速率G_l=6 kg/(m²?h)时堆平均温度随时间的变化

Fig.2  Variations of heap average temperature with bio- leaching time at irrigation rate of 6 kg/(m²?h)

图3 喷淋液体速率G_l=8 kg/(m²?h)时堆平均温度随时间的 变化

Fig.3  Variations of heap average temperature with bio- leaching time at irrigation rate of 8 kg/(m²?h)

图4  喷淋液体速率G_l=10 kg/(m²?h)时堆平均温度随时间的变化

Fig.4  Variations of heap average temperature with bio- leaching time at irrigation rate of 10 kg/(m²?h)

2.2  堆内平均温度与堆高的关系

图5所示为G_l=4 kg/(m²?h)时，堆内平均温度与堆高的关系。图5中曲线代表在该喷淋液流速率下堆的平均温度沿堆高的分布状况，在堆的顶部平均温度较

图5  喷淋液体速率G_l=4 kg/(m²?h)时堆平均温度随堆高的变化

Fig.5  Variations of average temperature with heap height at irrigation rate of 4 kg/(m²?h)

高，且对不同的气流速率，堆中同一高度温度相差较大；当气流速率在G_a=0.5和1.0 kg/(m²?h)时，从顶部到堆中6 m深处，温度虽呈下降趋势，但下降趋势缓慢，上下温差较小；而当G_a在2.5 kg/(m²?h)以上时，温度随高度下降明显，高温区主要集中在顶部0~1 m处，且平均温度总体较低，最高温度处较G_a=0.5 kg/(m²?h)时低20~30 ℃。这是由于在喷淋速率较小时，热量被气流带至堆的顶部积聚造成。

图6和7所示分别为堆内平均温度分布与堆高的关系。从图6和7看出，在该喷淋速率分别为6、8、1.0 kg/(m²?h)时，温度随堆高的分布发生较大变化，温度最高点已不在堆的顶部，而在堆高6 m以下区域，说明此时，热量主要由液体带到堆下部而积聚。而G_a在5.0、4.0、3.0、2.0 kg/(m²?h)时的堆内温度变化与分

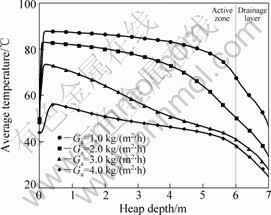
图6  喷淋液体速率G_l=6 kg/(m²?h)时堆平均温度随堆高的变化

Fig.6  Variations of average temperature with heap height at irrigation rate of 6 kg/(m²?h)

图7  喷淋液体速率G_l=8 kg/(m²?h)时堆平均温度随堆高的变化

Fig.7  Variations of average temperature with heap height at irrigation rate of 8 kg/(m²?h)

布趋势则与前二者相同，即随气流速率的上升，堆内平均温度反而下降，且在5.0 kg/(m²?h)时堆内温度最低。

图8所示为G_l=10 kg/(m²?h)时，堆内平均温度分布与堆高的关系。与图7相比可知，由于喷淋速率的加大，在堆顶和堆底部保持相同温度分布时，可适当加大气体的流速，如保持顶部平均温度在55~80 ℃范围时，相应气体流速可为3.0 kg/(m²?h)，而喷淋速率G_l=8 kg/(m²?h)时相应气体流速可为1.0 kg/(m²?h)。与前者相同的是，当喷淋速率较大时，若气体流速过小，则堆中整个平均温度较低，不利于生物浸出。

图8  喷淋液体速率G_l=10 kg/(m²?h)时堆平均温度随堆高的变化

Fig.8  Variations of average temperature with heap height at irrigation rate of 10 kg/(m²?h)

2.3  最大平均堆温与喷淋速率的关系

从图1~8可知，一般情况下，堆中平均温度在浸出20~30 d时会有明显上升，30 d以后，温度不再上升，达到最大值；在不同的G_l下，当G_a在一定范围内减小时，平均堆温均呈上升趋势，但G_a相对于G_l有一定限度；当G_a过小时，堆平均温度不再上升，反而下降，同时，温度沿堆高变化的趋势也会不同，且不同G_l相对的边界G_a值也不同。

在不同的G_l下，最大堆温与G_a的关系如图9所示。由图9可见，G_l=4、6 kg/(m²?h)时，最高温度可达到85 ℃，当G_a分别在0.5与1.0 kg/(m²?h)以上时，温度逐步下降；而对于G_l=8、10 kg/(m²?h)，当G_a分别在2.0与1.0 kg/(m²?h)时，堆中平均温度最高，G_a过小，则气体在液体压力下难以在堆中扩散，反应受阻；同时，大量热被液体带走，堆中温度急剧下降，同样，当G_a过大时，由于气体对流影响，热量随蒸发气体散失。可见堆中平均温度的变化与堆中温度沿高度的分布不仅仅与G_l、G_a有关，更重要的是与G_a/G_l的比值有很大关系。

图9  最大平均堆温与喷淋速率的关系

Fig.9  Relationship between maximum average temperature and air flow rate at different irrigation rates

2.4  不同气流速率与液流速率之比时堆平均温度的分布

图10所示在反应产热率S₀=20 W/m³、G_l=5 kg/(m²?h)、浸出75 d、不同G_a/G_l条件下，堆中温度的分布曲线。由图10可知，当G_a/G_l为1/6时，堆中最大温度仅38 ℃左右，且堆的底部底流区域温度较高，而顶部温度较低，大量热量积聚在堆的底部。而当G_a/G_l= 2/3时，最高温度可达到45 ℃， 且温度较高区域主要分布在堆顶部1 m范围，而堆底部温度较低，且下降较快。可见，除确定合理的喷淋液流速率G_l

图10  不同G_a/G_l下堆中平均温度随堆高的变化 (G_l=5 kg/(m²?h))

Fig.10  Variations of average temperature with heap height at different G_a/G_l values

和气体流速G_a外，它们的比例关系G_a/G_l对于堆内温度的大小及分布十分重要。如当G_a/G_l在1/6时，相对于液流速率，气流速率偏小，大约为0.83 kg/(m²?h)，此时，热量积聚在底部，大量热量被溶液带走，而堆表面由于蒸发又损失大量热量，使顶部过冷，从而在堆的表面会形成一低温层，与G_a/G_l=1/3相比较，气流速率加大，尽管相对于喷啉液流速率上仍较小，温度分布总体趋势仍和G_a/G_l=1/6时相同，由顶部到底部温度呈上升趋势，但堆平均温度较高，反应放热量增加。当气体流速继续增加，G_a/G_l为1/2、2/3、5/6和1时，由于气体的对流作用，气体将更多的热量带到堆的上部，并在上部区域逐渐产生热的净积聚，此时堆内温度的分布趋势较G_a/G_l=1/3和G_a/G_l=1/6时发生了变化，高温区分布在堆的顶部区域，且温度由顶部到底部呈下降趋势。但是过大的气体流速会使热量损失，所以在实际堆浸中，气体速率有一最佳值，在G_l一定时其值取决于G_a/G_l。如图10所示，G_a/G_l大于1/3时，堆中温度上升，高温区域向堆上部转移，但当G_a/G_l从1/2增加到1时，尽管温度分布的趋势没变，但堆中温度呈下降趋势。

3  结论

1) 堆浸过程中反应速率、细菌的生长代谢等许多因素与堆中的温度大小和分布相关。若要实现次生硫化铜矿的高效浸出，则必须掌握堆中温度变化及分布规律。

2) 基于生物冶金与冶金热力学、动力学基础，可建立堆中温度热平衡方程，方程包含热传导、热对流和热辐射三项。掌握堆中温度的变化与分布规律可通过热平衡方程和数学彷真的方法来说明。

3)堆中温度变化与分布规律与喷淋液流速率G_l、气流速率G_a均有很大关系；不仅与各自大小直接相关，且与G_a/G_l大小关系密切。若喷淋液流速率G_l过大，堆中热量积聚于堆的底部；若气流速率过大，则热通过对流上升到堆的顶部，过大的液流速率和气流速率均会导致热量通过底部和顶部蒸发损失，合理的G_a/G_l取值是实现堆中温度理想分布的途径。

REFERENCES

[1] MOOIMAN M B, SOLE K C, KINNEBERG D J. Challenging the traditional hydrometallurgy curriculum an industry perspective[J]. Hydrometallurgy, 2005, 79: 80-88.

[2] BRIERLEY J A, BRIERLEY C L. Present and future commercial applications of biohydrometallurgy[J]. Hydrometallurgy, 2001, 59: 233-239.

[3] EHRLICH H L. Past, present and future of biohydrometallurgy[J]. Hydrometallurgy, 2001, 59: 127-134.

[4] AKCIL A. Potential bioleaching developments towards commercial reality[J]. Minerals Engineering, 2004, 17: 477-480.

[5] BRIERLEY C L. Bacterial succession in bioheap leaching[J]. Hydrometallurgy, 2001, 59: 249-255.

[6] LIZAMA H M. A kinetic description of percolation bioleaching[J]. Minerals Engineering, 2004, 17: 23-32.

[7] PADILLA G A, CISTERNAS L A, CUETO J Y. On the optimization of heap leaching[J]. Minerals Engineering, 2008, 21(9): 673-678.

[8] 李宏煦, 苍大强, 邱冠周, 吴爱祥. 溶液电位及堆结构影响次生硫化铜矿生物堆浸的动力学[J]. 中南大学学报: 自然科学版, 2006, 37(6): 1087-1093.
LI Hong-xu, CANG Da-qiang, QIU Guan-zhou, WU Ai-xiang. Kinetics of secondary copper sulf ide heap bioleaching concerning potential and heap constitution[J]. Journal of Central South University: Science and Technology, 2006, 37(6): 1087-1093.

[9] 李宏煦, 苍大强, 陈景河, 邱冠周. 生物因素对次生硫化铜矿堆浸过程动力学的影响[J]. 中国有色金属学报, 2007, 17(2): 331-335.
LI Hong-xu, CANG Da-qiang, CHEN Jing-he, QIU Guan-zhou. Effect of biological factors on heap bioleaching kinetics of secondary copper sulfide[J]. The Chinese Journal of Nonferrous Metals, 2007, 17(2): 331-335.

[10] 李宏煦, 王淀佐, 陈景河. 细菌浸矿作用分析[J]. 有色金属, 2003, 55(3): 68-71.
LI Hong-xu, WANG Dian-zuo, CHEN Jing-he. Description of microbe effects on sulfide mineral bioleaching[J]. Nonferrous Metals, 2003, 55(3): 68-71.

[11] 李宏煦, 王淀佐. 生物冶金中的微生物及其作用[J]. 有色金属, 2003, 55(2): 60-63.
LI Hong-xu, WANG Dian-zuo. Review of investigation on microorganism behavior in ore bioleaching[J]. Nonferrous Metals, 2003, 55(2): 60-63.

[12] 李宏煦, 董清海, 苍大强, 王淀佐. 高温浸矿菌sulfolobus的生长及浸矿性能[J]. 北京科技大学学报, 2007, 29(1): 20-24.
LI Hong-xu, DONG Qing-hai, CANG Da-qiang, WANG Dian-zuo. Thermophilic microorganism sulfolobus growth and leaching chalcopyrite properties[J]. Journal of University of Science and Technology Beijing, 2007, 29(1): 20-24.

[13] 李宏煦, 王淀佐, 陈景河. 细菌浸矿的间接作用分析[J]. 有色金属, 2003, 55(4): 98-100.
LI Hong-xu, WANG Dian-zuo, CHEN Jing-he. Discussion on indirect mechanism of bioleaching[J]. Nonferrous Metals, 2003, 55(4): 98-100.

[14] SIDBORN M, CASAS J, MART?NEZ J. Two-dimensional dynamic model of a copper sulphide ore bed[J]. Hydrometallurgy, 2003, 71(1/2): 67-74.

[15] 李宏煦, 陈景河, 王淀佐. 福建紫金矿业股份有限公司硫化铜矿生物堆浸过程[J]. 有色金属, 2004, 56(4): 66-69.
LI Hong-xu, CHEN Jing-he, WANG Dian-zuo. Copper sulfide dump bioleaching in Fujian Zijin Mining Industry Corporation[J]. Nonferrous Metals, 2004, 56(4): 66-69.

[16] LI Hong-xu, WANG Dian-zuo, QIU Guan-zhou, HU Yue-hua. Growth kinetics of Thiobacillus ferrooxidans in bioelectrochemical cell[J]. Journal of Central South University of Technology, 2004, 11(1): 36-40.

[17] GATTI M N, MILOCCO R H, GIAVENO A. Modeling the bacterial oxidation of ferrous iron with Acidithiobacillus ferrooxidans using kriging interpolation[J]. Hydrometallurgy, 2003, 71: 89-96.

[18] 李宏煦. 硫化铜矿生物堆浸过程的动力学仿真与优化研究 [D]. 北京: 有色金属研究总院, 2004.
LI Hong-xu. The kinetics and simulation studies of copper sulfide bio heap leaching process (Postdoctoral thesis)[D]. Beiing: General Research Institute of Nonferrous Metallurgy, 2004.

[19] MELLADO M E, CISTERNAS L A, G?LVEZ E D. An analytical model approach to heap leaching[J]. Hydrometallurgy, 2009, 95(1/2): 33-38.

[20] CARIAGA E, CONCHA F, SEP?LVEDA M. Convergence of a MFE-FV method for two phase flow with applications to heap leaching of copper ores[J]. Computer Methods in Applied Mechanics and Engineering, 2007, 196(25/28): 2541-2554.

[21] DAVID G. Dixon analysis of heat conservation during copper sulphide heap leaching[J]. Hydrometallurgy, 2000, 58: 27-41.

[22] MOUSAVI S M, JAFARI A, YAGHMAEI S, VOSSOUGHI M, SARKOMAA P. Computer simulation of fluid motion in a porous bed using a volume of fluid method: Application in heap leaching[J]. Minerals Engineering, 2006, 19(10): 1077-1083.

(编辑 龙怀中)

基金项目：国家重点基础研究发展计划资助项目(2010CB630905)；国家自然科学基金资助项目(20876014)

收稿日期：2009-07-15；修订日期：2010-01-08

通信作者：李宏煦，副教授，博士；电话：010-62332786；E-mail：lihongxu2001@126.com；lihongxu2001@sina.com