Calculation of maximum surface settlement induced by EPB shield tunnelling and introducing most effective parameter
来源期刊:中南大学学报(英文版)2016年第12期
论文作者:Sayed Rahim Moeinossadat Kaveh Ahangari Kourosh Shahriar
文章页码:3273 - 3283
Key words:surface settlement; shallow tunnel; tunnel boring machine (TBM); multiple regression (MR); adaptive neuro-fuzzy inference system (ANFIS); cosine amplitude method (CAM)
Abstract: This study aims to predict ground surface settlement due to shallow tunneling and introduce the most affecting parameters on this phenomenon. Based on data collected from Shanghai LRT Line 2 project undertaken by TBM-EPB method, this research has considered the tunnel’s geometric, strength, and operational factors as the dependent variables. At first, multiple regression (MR) method was used to propose equations based on various parameters. The results indicated the dependency of surface settlement on many parameters so that the interactions among different parameters make it impossible to use MR method as it leads to equations of poor accuracy. As such, adaptive neuro-fuzzy inference system (ANFIS), was used to evaluate its capabilities in terms of predicting surface settlement. Among generated ANFIS models, the model with all input parameters considered produced the best prediction, so as its associated R2 in the test phase was obtained to be 0.957. The equations and models in which operational factors were taken into consideration gave better prediction results indicating larger relative effect of such factors. For sensitivity analysis of ANFIS model, cosine amplitude method (CAM) was employed; among other dependent variables, fill factor of grouting (n) and grouting pressure (P) were identified as the most affecting parameters.
J. Cent. South Univ. (2016) 23: 3273-3283
DOI: 10.1007/s11771-016-3393-5

Sayed Rahim Moeinossadat1, Kaveh Ahangari1, Kourosh Shahriar2
1. Department of Mining Engineering, Science and Research Branch, Islamic Azad University, Tehran, Iran;
2. Department of Mining and Metallurgical Engineering, Amirkabir University of Technology, Tehran, Iran
 Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Abstract: This study aims to predict ground surface settlement due to shallow tunneling and introduce the most affecting parameters on this phenomenon. Based on data collected from Shanghai LRT Line 2 project undertaken by TBM-EPB method, this research has considered the tunnel’s geometric, strength, and operational factors as the dependent variables. At first, multiple regression (MR) method was used to propose equations based on various parameters. The results indicated the dependency of surface settlement on many parameters so that the interactions among different parameters make it impossible to use MR method as it leads to equations of poor accuracy. As such, adaptive neuro-fuzzy inference system (ANFIS), was used to evaluate its capabilities in terms of predicting surface settlement. Among generated ANFIS models, the model with all input parameters considered produced the best prediction, so as its associated R2 in the test phase was obtained to be 0.957. The equations and models in which operational factors were taken into consideration gave better prediction results indicating larger relative effect of such factors. For sensitivity analysis of ANFIS model, cosine amplitude method (CAM) was employed; among other dependent variables, fill factor of grouting (n) and grouting pressure (P) were identified as the most affecting parameters.
Key words: surface settlement; shallow tunnel; tunnel boring machine (TBM); multiple regression (MR); adaptive neuro-fuzzy inference system (ANFIS); cosine amplitude method (CAM)
1 Introduction
Tunnel construction in urban areas is not as easy as it is in non-residential areas. Most of tunnels built along railways, roads, and particularly subways are constructed in shallow depths of soft grounds found within urban areas (subsurface structures’ foundations or beside important urban facilities). Deformations (specially the settlement) are a common phenomenon in the course of tunneling process [1]. On the other hand, in most of such projects, it is not possible to make a change in the tunnel’s path to reach a reliable ground. Therefore, it is necessary to protect underground structures and facilities against possible damages resulted from tunneling process. As such, the tunnel should be constructed in such a way to induce minimum deformation on the ground surface, so as to minimize the damages experienced by surface structures. The mentioned points reveal the importance of proper analysis, support, compatibility of construction method and instrumentation [2].
In order to be able to control the settlement, one should be able to predict it, based on which one may consider required preventions and protections. Settlement prevention and control methods are completely dependent on the settlement prediction method, further indicating the importance of settlement prediction. Accordingly, a tunnel engineer needs to be able to make reliable prediction of ground deformations induced by tunneling.
The selection of appropriate method depends on the complexity of the problems [3]. To predict settlement and other tunnel deformations, many methods were proposed (such as analytical, empirical, numerical, etc.) each with its strengths, contributing to the problem expression in one way or another, and weaknesses as well. The most important weakness of the proposed methods is that they fail to consider all parameters contributing to the settlement. Although some advancements have been realized in the ability to propose ground movement during recent years, but the most advanced method has several pitfalls. PECK [4] addressed the issues associated with soft ground tunneling, and proposed an empirical relation based on field observations of several tunneling projects. The empirical relation has become a classical framework widely used for predicting tunneling-induced ground movement. However, at the time of PECK’s work, tunneling was mainly accomplished using either hand mining methods or open faced shield methods, including several under compressed air. As a result, ground movements caused by the tunneling methods used at that time depended more on geological conditions than on the tunneling operational parameters. Empirical methods relating geological conditions to surface settlements were developed on this basis. However, at present, EPB (earth pressure balance) shield has been used in most of recent soft ground tunneling projects around the world. In this tunneling method, there are many factors including ground condition, operational parameters, and tunnel geometry affecting the magnitude of surface settlement. Therefore, it is difficult to predict the settlement only by the classical method. Although analytical relations exist between shield tunnel characteristics and surface settlements; also numerical methods (FEM and …) have been applied to tunneling problems but all affecting parameters still cannot be included in the solutions [5].
To overcome these limitations, intelligent methods can be used to develop a more accurate and reliable predictive method. In the recent decade, intelligent approaches have found a special position within the efforts toward estimating the settlement as well as other tunnel deformations. Various researchers have used such methods as artificial neural network (ANN), fuzzy logic (FL), support vector machine (SVM), gene expression programming (GEP) to present models to predict settlement and other tunnel deformations; the results indicate high relative accuracy of these methods [3, 6-12]. In this investigation, first, MR method was used to present a set of equations to predict the maximum surface settlement. Then, as an intelligent method, ANFIS was used to enhance the accuracy of the results. ANFIS enjoys the advantages of both neural and fuzzy systems. It is particularly the alternative of choice in cases where the number of available datasets to be used for modeling is low. Most geoscience-related problems do not come with a large deal of available data; the present research, as well, suffers from such issue. For example, this method is selected to be used to predict surface settlement in this research.
In spite of numerous advantages provided by intelligent methods, a large deal of researches conducted on such methods have referred to their pitfalls. The main disadvantage associated with these methods is that they model the settlement without considering the main affecting factors. As an example, many researches have ignored tunnel support parameter. It is clear that a tunnel with no support will induce as large deformations as the tunnel is likely to be unstable. Therefore, such main factors as operational factors should be considered when modeling and predicting surface settlement.
Made up of numerous inputs, yet intelligent methods provide enhanced accuracy, they can be used for upcoming sections of the corresponding tunnel or similar tunnels only when all inputs are available, namely, lack of even a single input parameter makes it impossible to employ the generated model. In the present investigation, we have tried to build different models based on different sets of input parameters, so as to not only evaluate their efficiency, but also to study the effect of their presence or absence on the surface settlement prediction. Accordingly, several intelligent models and equations were generated based on different sets of input parameters (in terms of type and number), so as the engineers working within this field can employ the model in which all input parameters required are taken into consideration.
Among few studies already dealt with settlement prediction using ANFIS method one may refer to the works by HOU et al [13] and AHANGARI et al [12]. HOU et al [13] used such dependent parameters as surface settlement (at 5 points) behind the tunnel face and one operational parameter (working cycles per day) to predict surface settlement 5 m ahead of the shield face. As such, no geometric, strength, or alike factors was considered in their investigations. AHANGARI et al [12] paid particular attention to geometric and strength factors; however, they ignored operational factors such as tunnel support parameters. Furthermore, the settlement parameter used in their investigation was not the actual settlement (measured), but the one resulted from numerical modeling (FLAC2D).
The novelty of the employed intelligent method, elimination of existing pitfalls within previous researches, and higher accuracy of the models developed in the present study compared to those in Ref. [14] indicate higher reliability of the results obtained in the present research. Finally, for sensitivity analysis of ANFIS model and determination of the effect amount of input parameters, CAM method was undertaken. Various researchers have already proved the performance of CAM method which is related to the dot product for the cosine function [15].
2 Case study
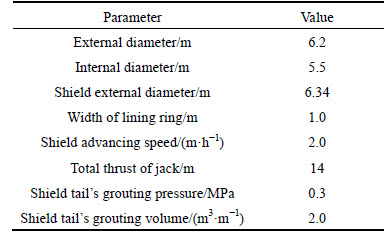
The study scope of this research is Shanghai LRT Line 2 project. All required information was gathered from a specific research [14]. The tunneling project between Pudong South Road Station and Nanpu Bridge Station was an important component of this project as well as a major project in Shanghai. The tunnel was started from the end well west to Pudong South Road Station to the end well east to Nanpu Bridge Station, with the full length of up line 1997.148 m and down line 1981.960 m. Also, the soil type of the project area was mainly silty clay and the tunnel was constructed using TBM-EPB approach. The other properties of this project are summarized in Table 1.
Table 1 Some of technical characteristics of shield in project of Shanghai LRT Line 2
3 Factors affecting surface settlement
Based upon case history reviews [8, 11], the factors causing settlements can be grouped into three major categories. These parameters summarized in Table 2 are used as input data for predicting the maximum surface settlement. Figure 1 shows the maximum surface settlement versus nine affecting parameters in Shanghai LRT Line 2 Project. It is clear that there are further parameters contributing into the tunnel settlement; however, they are ignored as many of them (such as segment thickness and length, TBM length) were constant in the course of tunneling project.
Table 2 Summary of factors affecting maximum surface settlement (Smax)

3.1 Tunnel geometry factors
Factors addressed in this section are two geometric factors, namely the tunnel depth (H) and diameter (D). Here, tunnel diameter is the same as drilling diameter which is determined by the shield’s outer diameter. This parameter plays a major role in the development of ground settlement. As the diameter increases, the roof length is immediately increased and so is the area of the surface to be self-supported. As the maximum convergence rate occurs within a region around the face covering an area of a diameter equal to that of the tunnel, by increasing the tunnel diameter, the affected region around the face extends makes it more difficult to control the convergence. Furthermore, by increasing the tunnel diameter, effective incorporation of temporary support system is reduced, so that tunneling in such loose grounds will require extended provisions and particular considerations. Tunnel depth is another effective parameter on the settlement development within the ground above the tunnel. Obviously, the tunnel provided is deep enough, roof falls resulted effects will be petered out before reaching the surface [16]. Nevertheless, the effect of tunnel depth on the settlement should always be considered along with those of tunnel diameter. Accordingly, one may use depth to diameter ratio (H/D) to simultaneously investigate their effects. Referring to Figs. 1(a) and (b), an approximately suitable relation exists between the tunnel depth (H) and surface settlement (Smax). This is why tunnel diameter changes within a limited range with the corresponding figure not showing any significant trend.
3.2 Soil strength factors
Tunneling into soft ground requires a greater deal of safety provisions compared to those provided under hard rock conditions. Shallow tunnels are usually drilled into soft grounds necessitating particular considerations in terms of tunnel’s temporary support system. Failure to incorporate an effective supporting system of high efficiency, poor ground properties will boost tunnel roof fall probability. Therefore, it will be very useful to incorporate TBM-EPB drilling approach under such conditions. According to the mentioned issues, the higher the strength of the tunnel encompassing mass is, the easier the tunneling process leading to lower settlement will be. In order to predict the maximum surface settlement in this research, three parameters were considered: cohesion force (C), internal friction angle (f), and modulus of elasticity (Es). Figures 1(c) to (e) illustrate the value of these parameters versus the resulted settlement. According to these figures, the three parameters have similar effect on the settlement. Denoted part of the figures demonstrates a situation where similar parameters have produced different settlement values. This is an indication of other parameters (either geometric or operational) affecting the settlement. Therefore, it seems clear that other affecting factors than strength ones should be considered.
3.3 Shield operational factors
Four operational factors are considered. The penetration rate measures how fast the shield can move forward. In practice, to achieve an EPB mode, shield operators should control the rate of spoil extraction to correspond to the penetration rate. If the extraction rate is too high compared to the penetration rate, it means that the shield excavates too much volume of soil relative to the volume replaced by the advancing shield. As a result, the excavated volume of the soil becomes unbalanced with the volume of soil that is occupied by the shield advance so that ground loss would be expected. On the other hand, if the extraction rate is too low compared to the penetration rate, it means that the volume of excavation is less than the volume replaced by the shield advance. As a result, the shield may generate too high a face pressure. The most important factor affecting the penetration rate is the capacity or speed of the soil removal system [8]. As shown Fig. 1(f), it is still difficult to establish a clear relationship between the penetration rate and the maximum surface settlement. Relatively similar issues are seen for the relation between the thrust force and surface settlement. The thrust force is the force which drives the shield forward against frictional forces as well as required supporting pressure (if any). This operational parameter is largely related to the penetration rate. The penetration rate increases as the thrust force is raised up to an optimum level beyond which an inverse effect is resulted, so that the discs will be likely to stuck and reduce the penetration rate. Accordingly, just like what was expressed regarding the relation between the penetration rate and settlement, generally it can say that a rise in thrust force causes an increase in the tunnel face pressure, while a decrease in the thrust force makes the ground subside resulting in surface settlement. Although, according to Fig. 1(g), a relatively clear relationship exists between the thrust force and the maximum surface settlement, but it is not yet possible to make an accurate judgment on this case.
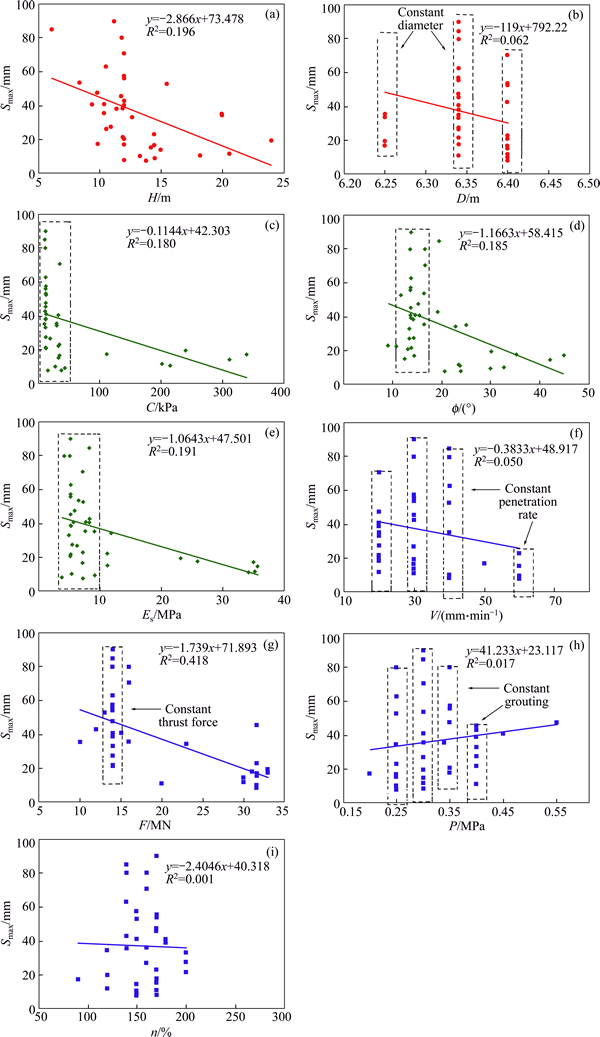
Fig. 1 Effective parameters versus maximum surface settlement
Quality of tail void grouting also contributes to the extent of the ground settlement. As the shield is jacked forward, a tail void around the outside of the lining is built as shown in Fig. 2(a). Tail void grouting is necessary in order to prevent ground from moving towards the void. In general practice, grouting pressure (P) should be high enough to guarantee the flow of grout material and to resist the ground moving into the void as shown in Fig. 2(b). Another criterion to check the grouting performance is percent grout filling (n) that has to be maintained at a level higher than the theoretical void as also shown in Fig. 2(b). Tunneling operations with high P and n can considerably reduce settlements developed after the shield passing [8]. As can be seen from Figs. 1(h), (i), both of the grouting pressure and grouting fill factor approximately are constant, but the maximum surface settlements were found to vary significantly. A clear relationship cannot be established from the plot. This may be caused by the fact that surface settlements can be also affected by other parameters.
According to Fig. 1, there are no strong trends in the relationship between each parameter and the maximum surface settlement. Only in the plots of the tunnel depth versus the maximum surface settlements, small trends were observed. This indicates that more than one parameter influences the magnitude of surface settlements. In practice, it is impossible to hold the other parameters constant while varying a parameter for investigating the effect of the parameter on surface settlements. Furthermore, even though large amounts of data were recorded, sensitivity analysis can provide only limited results due to the complex behavior of EPB shield tunneling.
4 Multiple regression (MR) method
Multiple regression (MR) method is used to study or determine the relationships between different variables, including independent and dependent ones and might be used to analyze data or to generate a model. Many researchers have applied this particular method in various fields of geotechnical science [17-18]. Aimed at presenting an applied relation to predict the maximum surface settlement and investigate the effect of dependent variables, in this research SPSS software (Ver. 16.0) is used to propose several of multiple linear regression equations. According to Table 3, firstly, effects of geometric parameters of the tunnel were investigated and based on Eq. (1), the tunnel depth (H) and diameter (D) were selected as the dependent variables. As can be seen, the equation’s significance level is equal to zero, indicating the reliability of the model.
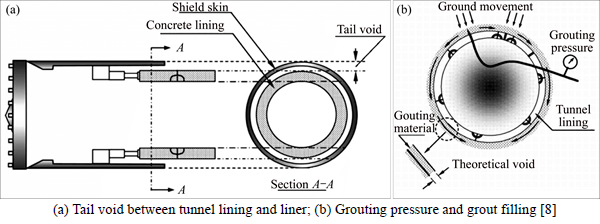
Fig. 2 Schematic diagram:
Table 3 Proposed MR equations for prediction of maximum surface settlement
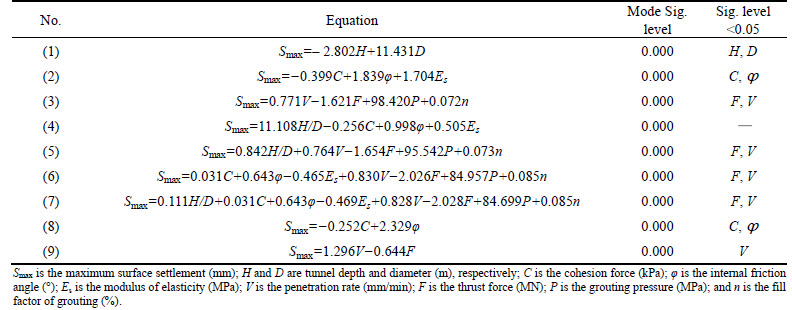
The general levels of significance are 10% (0.1), 5% (0.05), 1% (0.01), 0.5% (0.005), and 0.1% (0.001). The choice of significance level is somewhat arbitrary, but for many applications a level of 5% is chosen conventionally [18]. The significance level in Table 3 is zero; therefore, the presented MR model is valid since the maximum significance level is 0.05.
It is worth mentioning that the significance levels of both dependent variables within Eq. (1) are below 0.05, confirming their effective role within the respective equation. What investigated in Eq. (2) is the effect of strength parameters associated with the environment within which the tunnel is encompassed. According to Table 3, in spite of the fact that the significance level of the model is generally confirmed, the significance level for the parameter Es is above 0.05, indicating the this parameter possesses the lower significance. Similarly, Eq. (3) was proposed to address the third class of effective parameters (operational factors) on the settlement; among 4 dependent parameters in this class, only F and V were of significance levels below 5%.
Continuing with the application of MR, effective parameters were combined to compose new equations. Accordingly, Eq. (4) is composed of geometric and strength parameters; Eq. (5) is composed of geometric and operational parameters; Eq. (6) is composed of strength and operational parameters; and Eq. (7) includes all parameters. Considering limited variation range of tunnel diameter data in this research, one can enhance the model accuracy by reducing the number of dependent parameters. Therefore, tunnel depth to diameter ratio (H/D) was used in the combined equations to somehow reduce the problem complexity by quantitatively reducing the number of dependent parameters. None of dependent parameters incorporated into Eq. (4) satisfied the significance constraint. Similarly in Eqs. (5) to (7), parameters F and V enjoyed significance levels below 5% while other parameters were associated significance.
Knowing that the significance value of ES in Eq. (2) and also those of P and n in Eq. (3) were above 5%, it was tried to propose new equations with these parameters eliminated so as to promote the accuracy. Accordingly, Eq. (8) was modeled with only two strength parameters and Eq. (9) was modeled with the two remaining operational parameters. The model and the two dependent variables in Eq. (8) satisfied the significance level criteria; however, in Eq. (9), the only parameter with a significance level below 5% was the parameter V.
In this work, several statistical evaluation criteria were used to assess the performance of the applied methods. These criteria are mean absolute error (MAE), root mean square error (RMSE) and coefficient of determination (R2) respectively, given by Eqs. (10)-(12) [19].
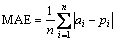 (10)
(10)
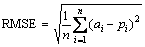 (11)
(11)
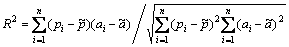 (12)
(12)
where a is the actual value of the maximum surface settlement; p is the predicted value of the maximum surface settlement; 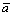 and
and 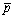 are the means of actual and predicted values of the maximum surface settlement respectively; n is the number of data sets.
are the means of actual and predicted values of the maximum surface settlement respectively; n is the number of data sets.
In order to compare and evaluate the accuracy of the predictions provided by the presented equations, R2, RMSE, and MAE criteria were employed, as shown in Fig. 3. According to this figure, completely similar variations were seen for RMSE and MAE criteria. That was why Eqs. (7), (6), (5), and (3) were associated with the least errors, respectively, and Eqs. (6), (7), (3), and (5) produced the highest determination coefficients, respectively.
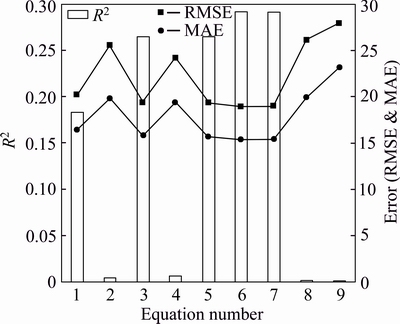
Fig. 3 Comparing values of R2, RMSE and MAE for predicting maximum surface settlement using MR equations
The priority of error and correlation criteria to select an equation to be used is a discussion which needs further deliberations. Since the values of R2 do not change by changing the model values equally and the function, ie RMSE, or MAE and etc., only shows the error and no correlation. The multi-objective error (MOE) function that is a combination of these metrics is most suitable criterion for evaluation of the performance of the models, given by Eq. 14 [20]. In this equation, RRMSE and R are calculated by Eqs. (14) and (15).
In Fig. 4, all MR equations are compared using MOE criterion. As indicted, Eqs. (5), (3), (7), and (6) were associated with the lowest MOEs with their predicting performance far superior over other equations. The common aspect of these four equations was the presence of operational factors. As such, one may suggest higher relative effect of operational factors compared to that of other factors. Furthermore, the accuracy provided by Eq. (1) was greater than that of Eq. (2), indicating larger effect of geometric factors compared to strength factors.
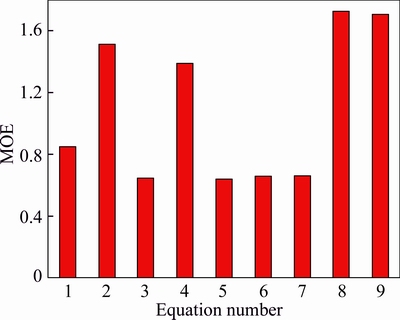
Fig. 4 Comparing MOE value for predicting maximum surface settlement using MR equations
Another notable point is the poor performance of Eqs. (8) and (9) when compared to Eqs. (2) and (3). Elimination of those parameters failing to satisfy the significance constraint, not only had not improved the results, but also had boosted the value of relative error. Therefore, although the significance level criteria extracted from the MR model had found the parameters Es, P, and n as being insignificant, but their presence had contributed into higher accuracy of the equations.
 (13)
(13)
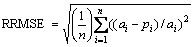 (14)
(14)
 (15)
(15)
5 Adaptive neuro-fuzzy inference system (ANFIS)
As observed in the previous section, surface settlement depends on many parameters with their interactions making the accuracy of the MR models very low. Under such circumstances, intelligent methods can be useful tools among which ANFIS method was used to predict the maximum surface settlement in the present investigations.
ANFIS is the integration of fuzzy logic (FL) and artificial neural network (ANN) introduced [21]. Fuzzy systems and ANNs include various advantages and disadvantages. A fuzzy system can model the qualitative aspects of human knowledge and reasoning processes, whereas it does not feature any earning capabilities. In other words, a fuzzy system cannot be trained. Nevertheless, neural networks are able to do self-training using datasets. Meanwhile, neural networks are implicit and they are unable to use human language [22]. To overcome these deficiencies, ANFIS has been proposed. ANFIS has the advantages of both fuzzy and neural systems [23]. According to Fig. 5, ANFIS process acts in five steps: Layer 1 is an input layer; Layer 2 is an input member functions layer (for fuzzification of inputs); Layer 3 is a rule layer; Layer 4 is an output member functions layer (for defuzzification of outputs) and layer 5 is an output layer [12]. In this system, training means that with the use of training dataset, the non-linear parameters related to the fuzzy membership functions at the first level and the linear parameters of the forth layer are determined in a way by which for each desired input, a favorable output is obtained. During this neuro-fuzzy process, membership function parameters are regulated through the back propagation (BP) algorithm or in combination with the least squares (LS) method [24-25].
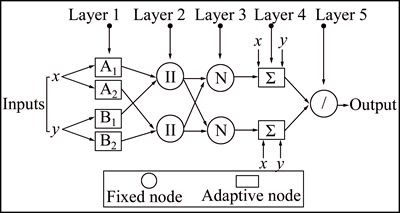
Fig. 5 ANFIS structure [25]
Using various methods of identification, different techniques to construct ANFIS model are available such as grid partitioning (GP), subtractive clustering method (SCM), fuzzy C-means clustering (FCM) [26]. In this study, to identify premise membership functions, all three aforementioned methods were used and the FCM generated the best result. So, this method is briefly described in the following.
5.1 Fuzzy C-means clustering (FCM)
The FCM is the most common method of fuzzy clustering. This method will place the data in related groups, based on their degree of membership. This method was introduced by BEZDEK [27] and, in fact, it is an optimized method of clustering such as the K-means method [12].
In this method, the numbers of clusters are divided as c numbers. Firstly, the cluster centers ci (i=1, 2, …, c) randomly from the n points {x1, x2, x3, …, xn} are selected. Second, the membership matrix u, using the following equation, is computed [26]:
 (16)
(16)
where dij is the Euclidean distance between the ith cluster center and the jth data point; u and m are the fuzziness index. Third, compute the cost function according to the next equation shown below.
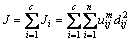 (17)
(17)
With the following condition:
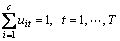 (18)
(18)
final step, compute new fuzzy cluster centers ci (i=1, 2, …, c) using the following equation:
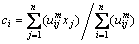 (19)
(19)
5.2 Estimation of maximum surface settlement by ANFIS
In this research, MATLAB software (Ver.: R2014a (8.3.0.532)) has been used for ANFIS modeling. As indicated in Table 4, to predict maximum surface settlement seven ANFIS models were proposed with their input parameters similar to MR Eqs. (1) to (7) (see Table 3). In order to build these models, it began with normalizing all data into [-1 1] interval, so as to get the variation ranges of the parameters closer to each other boosting the model ability to generalize and learn the relations among the parameters. Next, among total 41 available datasets, 12 datasets (about 30%) were considered for testing the models, while the remaining 29 datasets (about 70%) were utilized to build ANFIS models. Dataset division was performed in a random fashion and it was unchanged for all 7 models, so as to make their comparisons significant.
The best ANFIS structure was selected by using trial-and-error method. The type and number of membership functions, optimization algorithm, epochs, etc. were all optimized via trial-and-error approach. The built models were evaluated and compared based on RMSE values obtained for training and testing phases.
Table 4 Different models types and their parameters used for prediction of maximum surface settlement by ANFIS model
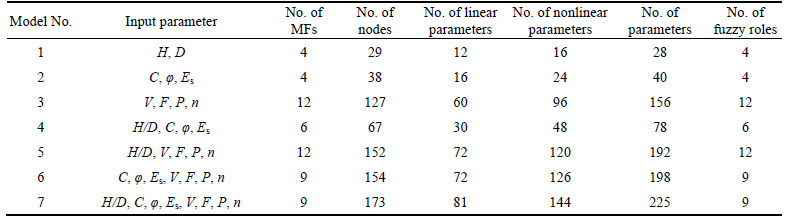
The membership function and optimization method for all models were Gaussian and hybrid, respectively. Other features of the built models are demonstrated in Table 4. Figure 6 depicts the structure of the 7th built ANFIS model (M7) including all input parameters. The model contains 5 layers with nine IF-THEN rules connected to each other via “and” operators.
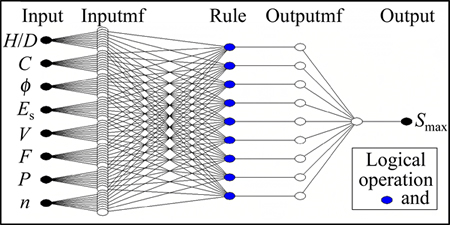
Fig. 6 ANFIS structure built to predict maximum surface settlement based on eight input parameters (M7)
The predicting results of the models in the training and testing phases based on R2, RMSE, and MAE criteria are listed in Table 5. As indicated in Fig. 7, in order to better compare the results, one may express that M7 and M4 provided the best and the worst prediction, respectively. It is worth mentioning that like what suggested with regards to MR equations, the models containing operational factors (M5-M7) were of higher relative accuracy. Low value of MOE in the training and testing phases was in an indication of the adequacy of the corresponding model, so that it can be generalized. Such model enjoys a good level of accuracy respect to raw data (test data).
Table 5 ANFIS models results to predict maximum surface settlement
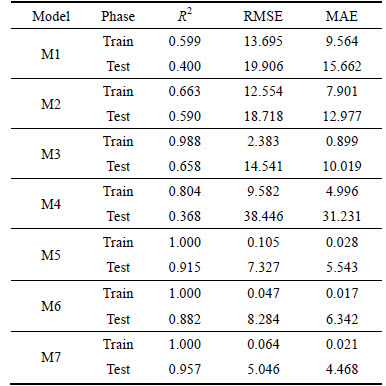

Fig. 7 Comparing MOE value for predicting maximum surface settlement using ANFIS models
5.3 Sensitivity analysis by cosine amplitude method (CAM)
In this work, the cosine amplitude method (CAM) is used to analyze sensitivity of the ANFIS model. By all the following methods, this similarity metric makes use of a collection of data samples, n data samples in particular. If these data samples are collected, they will form a data array, X [28],
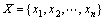 (20)
(20)
Each of the elements, xi, in the data array X is itself a vector of length m, that is,
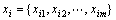 (21)
(21)
Hence, each of the data samples can be thought as a point in m-dimensional space, where each point needs m coordinates for a complete description. Each element of a relation, rij, results from a pairwise comparison of two data samples, xi and xj, where the strength of the relationship between data sample xi and data sample xj is given by the below membership strength:
 i, j=1, 2, …, n(22)
i, j=1, 2, …, n(22)
Close inspection of Eq. (22) reveals that this method is related to the dot product for the cosine function. When two vectors are collinear, their dot product is unity; when the two vectors are at right angles to one another, their dot product is zero [28].
In order to express the relation between the maximum surface settlement and the input parameters (in test phase), [1×12] sized matrices were obtained. The matrices obtained were correlated by means of the Eqs. (20) to (22), and the relation strengths (rij values) are shown in Fig. 8. According to this figure, the operational parameters n and P were associated with the largest effective, while strength parameters of C and Es provided the smallest effective into the maximum surface settlement. The figure is illustrating the effect of other parameters as well, larger effective of geometric factor (H/D) rather than strength parameters.
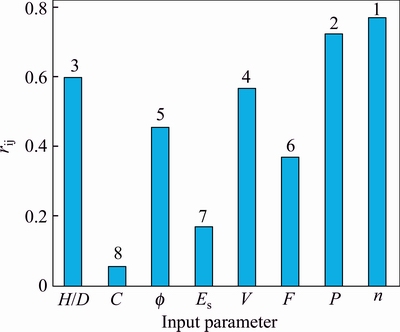
Fig. 8 Strength of relation (rij) between maximum surface settlement and input parameters
6 Comparing performance of methods
This research investigated the ability of two methods, namely MR and ANFIS, to predict the maximum surface settlement. As observed in Figs. 4 and 7, ANFIS was associated with much more accurate and reliable results compared to those of MR. For example, the value of MOE criterion for ANFIS model (M7) was much lower than the 7th MR equation (Eq. (7)) [0.126 versus 0.656], indicating considerable superiority of ANFIS model. As in contrast to MR method, ANFIS models the problem in two phases, they are of somehow different conditions when a comparison is concerned. As such, in order to perform a significant comparison, Eq. (23) was proposed, based on 29 datasets used in the training phase of ANFIS, to evaluate the performance of the two methods in terms of predicting 12 raw datasets. The significance level of newly proposed equation (Eq. (23)) was zero and the only dependent variable of less than 5% significance level being F.
Figure 9 demonstrates the predicted values by Eq. (23) and M7 along with the actual maximum surface settlement values. According to the figure, the predicted values by ANFIS model, in contrast to those of MR method, are close to actual values of the maximum surface settlement. The adjacency or overlapping of the two curves demonstrates that the predictions obtained by this intelligent method are in good agreement with the actual values, so that ANFIS has produced acceptable predicts across all settlement ranges.
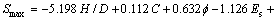
 (23)
(23)
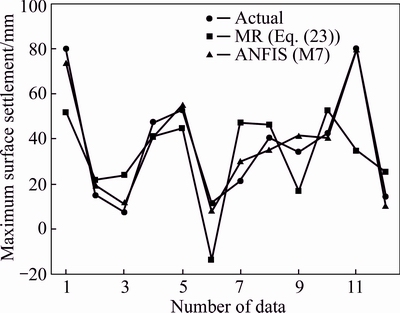
Fig. 9 Comparing actual of maximum surface settlement and predicted MR equation (Eq. (23)) and ANFIS model (M7)
7 Conclusions
Based on the results obtained in this research, it was clear that, due to the limited number of variables to be considered, MR method cannot be a suitable tool to predict the maximum surface settlement, whereas ANFIS model, in this context, was not limited in any sense. This intelligent method could reveal the relation between input parameters and their effects on output, and have the ability to intelligently generalize the new data.
In order to predict the maximum surface settlement based on various parameters, a total of nine MR equations and seven ANFIS models were proposed. Among other MR equations, Eqs. (8) and (9) were of lower accuracy when compared to similar equations (Eqs. (2) and (3)). Eliminating those parameters failing to satisfy the significance criteria, not only did not improve the results, but also gave rise to relative error value. Therefore, although the significance level criterion extracted from the MR model had found the parameters Es, P, and n as insignificant, their presence had contributed into higher accuracy of the equations. Regarding the ANFIS models, the one with all inputs considered (M7) was of the highest level of accuracy.
Those models and equations including operational factors (models M5, M6, and M7; Eqs. (7), (6), (5), and (3)) were of relatively results indicating larger effect of these factors on the settlement. Scrutinizing the effects of dependent variables, M7 (including all input parameters) was subjected to analyze sensitivity via CAM method. The results indicated that the largest effect on settlement variations come from operational factors followed by geometric and then strength factors. Among other variables, P and n were associated with the most intense effect, so that the settlement could be largely controlled via a proper high quality grouting operation. It is worth mentioning that these were introduced as the most effective variables whilst they were once recognized as the least affecting parameters via simple mathematical analysis shown in Fig. 1; this demonstrates the complexity involved in settlement predicting problems; no simple mathematical method is effective in this regard. CAM method recognized strength parameters of C and Es as the least affecting parameters; this shows the advantage of TBM-EPB tunneling method into loose grounds. High flexibility of this method within loose grounds clearly contributes to stability of the environment around the digging space largely reducing the settlement.
In order to control surface settlement, designing deeper tunnels may largely reduce the effects of roof falls before they reach ground surface. In most projects, however, due to various reasons, it is impossible to either change the tunnel path or increase its depth. Under such circumstances, the only relatively controllable factors are operational ones. As fill factor of grouting and grouting pressure were introduced as the most effective parameters in this research, one may largely reduce the settlement, particularly in shallow tunnels, by undertaking the grouting operation in as optimum fashion as possible.
References
[1] ATTEWELL P B, YEATES J, SELBY A R. Soil movements induced by tunnelling and their effects on pipelines and structures [M]. London: Blackies and Sons, Ltd, 1986.
[2] PALMSTROM A, STILLE H. Ground behaviour and rock engineering tools for underground excavations [J]. Tunnelling and Underground Space Technology, 2006, 22: 363-376.
[3] NEAUPANE K M, ADHIKARI N. Prediction of tunneling-induced ground movement with the multi-layer perceptron [J]. Tunnelling and Underground Space Technology, 2006, 21(2): 151-159.
[4] PECK R B. Deep excavation sand tunneling in soft ground [C]// Proceedings of the 7th International Conference on Soil Mechanics and Foundation Engineering. Mexico City, 1969: 225-290.
[5] SUWANSAWAT S. Using artificial neural networks for predicting surface settlements over twin tunnels [C]// International Symposium on Underground Excavation and Tunnelling. Bangkok, Thailand, 2006: 309-318.
[6] SHI J, ORTIGAO J, BAI J. Modular neural networks for predicting settlements during tunneling [J]. Journal of Geotechnical and Geoenvironmental Engineering, 1998, 124(5): 389-395.
[7] KIM C Y, BAE G, HONG S, PARK C, MOON H, SHIN H. Neural network based prediction of ground surface settlements due to tunnelling [J]. Computers and Geotechnics, 2001, 28(6): 517-547.
[8] SUWANSAWAT S, EINSTEIN H. Artificial neural networks for predicting the maximum surface settlement caused by EPB shield tunneling [J]. Tunnelling and Underground Space Technology, 2006, 21(2): 133-150.
[9] BOUBOU R, EMERIAULT F, KASTNER R. Artificial neural network application for the prediction of ground surface movements induced by shield tunnelling [J]. Canadian Geotechnical Journal, 2010, 47(11): 1214-1233.
[10] DARABI A, AHANGARI K, NOORZAD A, ARAB A. Subsidence estimation utilizing various approaches—A case study: Tehran No. 3 subway line [J]. Tunnelling and Underground Space Technology, 2012, 31: 117-127.
[11] OCAK I, SEKER S E. Calculation of surface settlements caused by EPBM tunneling using artificial neural network, SVM, and Gaussian processes [J]. Environmental Earth Sciences, 2013, 70(3): 1263- 1276.
[12] AHANGARI K, MOEINOSSADAT S R, BEHNIA D. Estimation of tunnelling-induced settlement by modern intelligent methods [J]. Soils and Foundations, 2015, 55: 737-748.
[13] HOU J, ZHANG M, TU M. Prediction of surface settlements induced by shield tunneling: An ANFIS model [M]. London: Taylor & Francis Group, 2009: 551-554.
[14] QIAO J, LIU J, GUO W, ZHANG Y. Artificial neural network to predict the surface maximum settlement by shield tunneling [C]// ICIRA’10 Proceedings of the Third International Conference on Intelligent Robotics and Applications. 2010: 257-265.
[15] JONG Y H, LEE C I. Influence of geological conditions on the powder factor for tunnel blasting [J]. International Journal of Rock Mechanics and Mining Sciences, 2004, 41(1): 533-538.
[16] WHITTAKER B, REDDISH D. Subsidence: Occurrence, prediction and control (Developments in geotechnical engineering, 56) [M]. Amsterdam: Elsevier, 1989.
[17] KHANDELWAL M, SINGH TN. Prediction of blast induced ground vibrations and frequency in opencast mine: a neural network approach [J]. Journal of Sound and Vibration, 2006, 289(4): 711-725.
[18] HAGHNEJAD A, AHANGARI K, NOORZAD A. Investigation on various relations between uniaxial compressive strength, elasticity and deformation modulus of asmari formation in Iran [J]. Arabian Journal for Science and Engineering, 2014, 39: 2677–2682.
[19] BEHNIA D, AHANGARI K, NOORZAD A, MOEINOSSADAT S R. Predicting crest settlement in concrete face rockfill dams using adaptive neuro-fuzzy inference system and gene expression programming intelligent methods [J]. Journal of Zhejiang University: Science A (Applied Physics & Engineering), 2013, 14(8): 589– 602.
[20] GARG A, TAI K, VIJAYARAGHAVAN V, SINGRU P M. Mathematical modelling of burr height of the drilling process using a statistical-based multi-gene genetic programming approach [J]. The International Journal of Advanced Manufacturing Technology, 2014, 73: 113–126.
[21] JANG J S R. ANFIS: Adaptive-network-based fuzzy inference systems [J]. IEEE Transactions on Systems, Man, and Cybernetics, 1993, 23(3): 665–685.
[22] KARTALOPOULOS S V. Understanding neural networks and fuzzy logic [M]// Basic Concepts and Applications. IEEE Press, 1996.
[23] JANG J S R, SUN C T. Neuro-fuzzy modeling and control [J]. Proceedings IEEE, 1997, 83(3): 378–406.
[24] JANG J S R, SUN C T, MIZUTANI E. Neuro-fuzzy and soft computing a computational approach to learning and machine intelligence [M]. New Jersey: Prentice Hall, 1997.
[25] BEHNIA D, MOEINOSSADAT S R, BEHNIA B, BEHNIA M, SAFARI-GORGI A, ZAKERIAN P. Prediction of settlement in sloping core rockfill dams using soft-computing [J]. Research in Civil and Environmental Engineering (RCEE), 2014, 2(2): 55–65.
[26] JALALIFAR H, MOJEDIFAR S, SAHEBI A A, NEZAMABADI- POUR H. Application of the adaptive neuro-fuzzy inference system for prediction of a rock engineering classification system [J]. Computers and Geotechnics, 2011, 38: 783–790.
[27] BEZDEK J. Fuzzy mathematics in pattern classification [D]. Ithaca: Cornell University, 1973.
[28] ROSE T J. Fuzzy logic with engineering applications [M]. 3rd ed. New Mexico: John Wiley & Sons, Ltd, 2010.
(Edited by YANG Hua)
Received date: 2015-10-26; Accepted date: 2016-01-30
Corresponding author: Kaveh Ahangari, Associate Professor, PhD; Tel: +982144868404; E-mail: kaveh.ahangari@gmail.com

