密排六方钛中基面堆垛层错导致的孪晶界滑移、孪生台阶及孪晶生长:第一性原理研究
来源期刊:中国有色金属学报(英文版)2021年第2期
论文作者:钱琦 刘正卿 江勇 王怡人 安星龙 宋旼
文章页码:382 - 390
关键词:孪晶界;层错;孪生台阶;孪晶生长;第一性原理
Key words:twin boundary; stacking fault; twinning disconnection; twin growth; first principles
摘 要:基于第一性原理计算研究密排六方结构钛中 共格孪晶界和滑移孪晶界的结构和能量,探讨滑移孪晶界的形成机理及其与孪晶生长的关系。结果表明,共格孪晶界与基面堆垛层错的相互作用可使共格孪晶界产生滑移,从而形成对应的滑移孪晶界。这种滑移最终能在孪晶界处形成一对单层孪生台阶,并恢复共格孪晶界的结构。孪生台阶的塞积可导致高分辨率透射电镜观察到的孪晶界上的台阶宽化,进一步促进孪晶的生长。此外,还评估多种合金化元素对孪晶界滑移的钉扎效应,为钛合金的强化设计提供指导。
Abstract: First-principles calculations were performed to investigate the structures and energetics of coherent twin boundaries (CTBs) and glide twin boundaries (GTBs) in hexagonal close-packed (hcp) Ti. The formation mechanism of GTBs and their correlation with twin growth were fundamentally explored. Results suggested that GTBs can form from the gliding of CTBs, through their interaction with basal stacking fault. The gliding eventually restored the CTB structures by forming a pair of single-layer twinning disconnections. The pile-up of twinning disconnections should be responsible for the wide steps at twin boundaries as observed in high-resolution transmission electron microscopy, which can further promote twin growth. Possible effects of various alloying elements on pinning twin boundaries were also evaluated, to guide the strengthening design of Ti alloys.
Trans. Nonferrous Met. Soc. China 31(2021) 382-390
Qi QIAN1*, Zheng-qing LIU1*, Yong JIANG1,2, Yi-ren WANG1, Xing-long AN2, Min SONG2
1. School of Materials Science and Engineering, Central South University, Changsha 410083, China;
2. State Key Laboratory of Powder Metallurgy, Central South University, Changsha 410083, China
Received 16 March 2020; accepted 6 September 2020
Abstract: First-principles calculations were performed to investigate the structures and energetics of  coherent twin boundaries (CTBs) and glide twin boundaries (GTBs) in hexagonal close-packed (hcp) Ti. The formation mechanism of GTBs and their correlation with twin growth were fundamentally explored. Results suggested that GTBs can form from the gliding of CTBs, through their interaction with basal stacking fault. The gliding eventually restored the CTB structures by forming a pair of single-layer twinning disconnections. The pile-up of twinning disconnections should be responsible for the wide steps at twin boundaries as observed in high-resolution transmission electron microscopy, which can further promote twin growth. Possible effects of various alloying elements on pinning twin boundaries were also evaluated, to guide the strengthening design of Ti alloys.
coherent twin boundaries (CTBs) and glide twin boundaries (GTBs) in hexagonal close-packed (hcp) Ti. The formation mechanism of GTBs and their correlation with twin growth were fundamentally explored. Results suggested that GTBs can form from the gliding of CTBs, through their interaction with basal stacking fault. The gliding eventually restored the CTB structures by forming a pair of single-layer twinning disconnections. The pile-up of twinning disconnections should be responsible for the wide steps at twin boundaries as observed in high-resolution transmission electron microscopy, which can further promote twin growth. Possible effects of various alloying elements on pinning twin boundaries were also evaluated, to guide the strengthening design of Ti alloys.
Key words: twin boundary; stacking fault; twinning disconnection; twin growth; first principles
1 Introduction
Twins are prone to form in crystals with low or medium stacking-fault energies [1], usually through the nucleation of faulted layers during the solidification [2], vapor deposition [3], or annealing recrystallization [4]. When crystal formability suffers seriously from a lack of independent slip systems (such as in plastically deformed hcp metals), or from the sharply increased stress of dislocation slip especially at low temperatures (such as in impact-loaded fcc-Cu [5] and bcc-Fe [6]), deformation twinning can also be induced. Deformation twins can even turn the unfavourably oriented grains to a more favourable slip orientation [7]. Typical twinning modes in the hcp crystals are 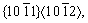
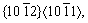
 and
and  [7,8]. The formation of twins has been generally believed to be closely related to partial dislocations and twinning disconnections (TDs) on non-basal twinning planes [7,9-12]. For instance,
[7,8]. The formation of twins has been generally believed to be closely related to partial dislocations and twinning disconnections (TDs) on non-basal twinning planes [7,9-12]. For instance, 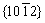 twins can nucleate from the simultaneous nucleation of multiple TDs, or perhaps more energetically favourably, from the simultaneous nucleation of non-basal partial dislocations and multiple TDs [12]. Such TDs can nucleate from non-planar dissociations of a, a+c, or c dislocations [13-16]. The twin can grow as TDs glide at the
twins can nucleate from the simultaneous nucleation of multiple TDs, or perhaps more energetically favourably, from the simultaneous nucleation of non-basal partial dislocations and multiple TDs [12]. Such TDs can nucleate from non-planar dissociations of a, a+c, or c dislocations [13-16]. The twin can grow as TDs glide at the 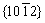 twin boundary. The core structure and high mobility of TDs have been identified by high- resolution transmission electron microscopy (HRTEM) [17,18]. Other mechanisms based on atomic shuffling and zonal dislocations also exist [19,20], but still have many details in debates.
twin boundary. The core structure and high mobility of TDs have been identified by high- resolution transmission electron microscopy (HRTEM) [17,18]. Other mechanisms based on atomic shuffling and zonal dislocations also exist [19,20], but still have many details in debates.
Coherent twin boundary (CTB) is the simplest structural version of twin boundaries (TBs), where the twin lattice is exactly a mirror reflection of the parent lattice [7,21]. Considerable theoretical efforts have been devoted to the structures and energetics of  and
and  CTBs in hcp Mg, Zr, and Ti, using various numerical methods including molecular statics (MS) [22], molecular dynamics (MD) [23], and first-principles density functional theory (DFT) [21,24,25]. Another major form of TBs is the glide twin boundary (GTB). The concept of GTB was firstly proposed for
CTBs in hcp Mg, Zr, and Ti, using various numerical methods including molecular statics (MS) [22], molecular dynamics (MD) [23], and first-principles density functional theory (DFT) [21,24,25]. Another major form of TBs is the glide twin boundary (GTB). The concept of GTB was firstly proposed for  twins [26], where GTBs were modeled by shifting one side lattice of CTB against the other along
twins [26], where GTBs were modeled by shifting one side lattice of CTB against the other along  on the twinning plane of
on the twinning plane of 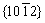 . Soon later,
. Soon later, 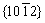 GTBs were observed by HRTEM characterizations in hcp Zn, and energetics calculations suggested that the GTBs could be preferred to forming under non- equilibrium conditions [27]. Recently, energetics calculations have been further extended to the
GTBs were observed by HRTEM characterizations in hcp Zn, and energetics calculations suggested that the GTBs could be preferred to forming under non- equilibrium conditions [27]. Recently, energetics calculations have been further extended to the 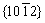 GTBs in hcp Mg and Au, as well as the
GTBs in hcp Mg and Au, as well as the  GTBs in hcp Mg and Au [28-31]. These GTBs were all predicted as high energy and metastable, as compared to their CTB counterparts, and their formation mechanism remains unclear.
GTBs in hcp Mg and Au [28-31]. These GTBs were all predicted as high energy and metastable, as compared to their CTB counterparts, and their formation mechanism remains unclear.
Basal dislocations can induce basal stacking faults (SFs) during deformation [32]. However, in contrast to a number of studies on non-basal partial dislocations, the roles of basal partial dislocations (and basal SFs) in twin growth are rarely studied. Very recently, the connection between basal SFs and twins has been experimentally suggested, based on the high-density presence of basal SFs inside  deformation twins under HRTEM [33]. Besides, profuse I1 SFs (defined as in hcp systems by removing one basal layer followed by a slip of
deformation twins under HRTEM [33]. Besides, profuse I1 SFs (defined as in hcp systems by removing one basal layer followed by a slip of  ) induced by basal dislocations were observed closely accompanying the growth of
) induced by basal dislocations were observed closely accompanying the growth of 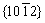 twins in pure Mg using in-situ tension experiments under transmission electron microscopy (TEM) [34]. MD simulations [35,36] also suggested that the intersection of one I1 SF with a
twins in pure Mg using in-situ tension experiments under transmission electron microscopy (TEM) [34]. MD simulations [35,36] also suggested that the intersection of one I1 SF with a  TB could emit a single-layer TD, which cannot glide along the TB but move by climbing to facilitate the development of twin embryos [35]. No first-principles efforts have been made to explore the complex interplays among basal SFs, TB gliding, TDs, and further twin growth, especially for both CTBs and GTBs in hcp systems.
TB could emit a single-layer TD, which cannot glide along the TB but move by climbing to facilitate the development of twin embryos [35]. No first-principles efforts have been made to explore the complex interplays among basal SFs, TB gliding, TDs, and further twin growth, especially for both CTBs and GTBs in hcp systems.
In this work, we take hcp Ti as an exemplary system and investigate the structures and energetics of  CTBs and GTBs from the first- principles, to gain important insights into the formation mechanism of GTBs and also its profound correlation with basal partial dislocations/ SFs, TDs, and twin growth.
CTBs and GTBs from the first- principles, to gain important insights into the formation mechanism of GTBs and also its profound correlation with basal partial dislocations/ SFs, TDs, and twin growth.
2 Methods
Experimental samples with dimensions of 40 mm × 10 mm × 3 mm were cut from a commercially pure Ti plate, annealed in vacuum at 650 °C for 1 h, and then cold-rolled to 40% thickness reduction. TEM specimens were then cut from the transverse section of the rolled sheets and ground to 50 μm in thickness. The HRTEM characterization was performed using a FEI Titan G2 60-300 TEM with an image spherical aberation corrector operated at 300 kV.
All the DFT calculations were conducted using Vienna ab-initio simulation package (VASP) [37] with the plane-wave basis sets and periodic boundary conditions. The electron-core interaction was described by the Blochl projector augmented wave method (PAW) within the frozen-core approximation [38]. The Perdew-Burke-Ernzerhof (PBE) generalized gradient approximation was employed for exchange-correlation functions [39]. Sandwich supercell models were employed to calculate the  ,
, 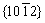 and
and  TB interfaces. All the ground-state configurations were optimized using a high energy cutoff of 475 eV for the plane-wave basis sets until the total energy was minimized and the total force on each ion converged within 0.02 eV/
TB interfaces. All the ground-state configurations were optimized using a high energy cutoff of 475 eV for the plane-wave basis sets until the total energy was minimized and the total force on each ion converged within 0.02 eV/ 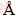 .
.
3 Results and discussion
3.1 Basic structures and energetic

Fig. 1 Schematics for  ,
,  , and
, and  twinning modes in hcp Ti (a) and
twinning modes in hcp Ti (a) and  projections of
projections of  ,
,  , and
, and  CTBs (b-d)
CTBs (b-d)
Figure 1(a) schematically illustrates the major twinning modes in hcp Ti lattice. Figures 1(b-d) show the projections of the corresponding CTBs along a1= . Hollow and solid balls denote atoms on two different neighboring
. Hollow and solid balls denote atoms on two different neighboring  planes. Dashed lines represent {0001} planes with an -ABABAB- stacking sequence, and solid frames highlight the conventional unit cells as viewed along a1. Interface formation energy (
planes. Dashed lines represent {0001} planes with an -ABABAB- stacking sequence, and solid frames highlight the conventional unit cells as viewed along a1. Interface formation energy ( ) was then calculated as
) was then calculated as
 (1)
(1)
where ECTB and Ebulk are the total energy of a fully relaxed CTB supercell and a pure bulk supercell with the exact same number of atoms, respectively, and A is the boundary area. The  ,
, 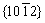 , and
, and  CTB supercells contain 64, 88, and 64 Ti atoms with periodic boundary conditions, respectively. Each supercell hosted two identical twin boundaries with a separation of at least 10
CTB supercells contain 64, 88, and 64 Ti atoms with periodic boundary conditions, respectively. Each supercell hosted two identical twin boundaries with a separation of at least 10 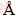 . Their dimensions along
. Their dimensions along  are all equal to the unit lattice parameter a. The other dimension along
are all equal to the unit lattice parameter a. The other dimension along  ,
,  , or
, or 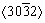 was chosen to equal
was chosen to equal 
 or
or  for
for  ,
, 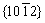 , or
, or  CTBs, respectively, to sufficiently cover one stacking period and retain the inversion symmetry. Accordingly, the Brillouin- zone integrations employed a 4×13×1, 4×8×1, and 2×15×2 Γ-centered Monkhorst-Pack K-mesh, respectively. Each supercell hosted two identical twin boundaries with a separation distance of more than 10
CTBs, respectively, to sufficiently cover one stacking period and retain the inversion symmetry. Accordingly, the Brillouin- zone integrations employed a 4×13×1, 4×8×1, and 2×15×2 Γ-centered Monkhorst-Pack K-mesh, respectively. Each supercell hosted two identical twin boundaries with a separation distance of more than 10  , to minimize the possible interaction. The calculated results are summarized in Table 1, showing good agreement with all previous DFT calculations. The
, to minimize the possible interaction. The calculated results are summarized in Table 1, showing good agreement with all previous DFT calculations. The  CTB has the lowest formation energy of 0.09 J/m2 only. The
CTB has the lowest formation energy of 0.09 J/m2 only. The  and
and  CTBs require higher formation energies but still lower than those of many symmetric-tilt grain boundaries (normally in the order of ~1 J/m2).
CTBs require higher formation energies but still lower than those of many symmetric-tilt grain boundaries (normally in the order of ~1 J/m2).
Table 1 Calculated interface energies of  CTBs in hcp Ti
CTBs in hcp Ti

Recall that GTBs can be constructed by gliding along the CTBs. Figure 2(a) shows the supercell for modeling  CTB in hcp Ti. Gliding the left half lattice by
CTB in hcp Ti. Gliding the left half lattice by  leads to a high energy and metastable
leads to a high energy and metastable  GTB in Fig. 2(b). After a full relaxation, the high energy
GTB in Fig. 2(b). After a full relaxation, the high energy  GTB can transform favorably back into the original CTB structure (with the lowest formation energy of γ=0.09 J/m2 only), accompanying with a left-shift of the twin boundary (Fig. 2(c)). Once such a gliding-and-shifting process occurs continuously, the
GTB can transform favorably back into the original CTB structure (with the lowest formation energy of γ=0.09 J/m2 only), accompanying with a left-shift of the twin boundary (Fig. 2(c)). Once such a gliding-and-shifting process occurs continuously, the  CTB can move consistently to the left. An opposite gliding of the left half lattice by
CTB can move consistently to the left. An opposite gliding of the left half lattice by  , however, cannot restore the original
, however, cannot restore the original  CTB structure but can result in a new and high energy structure of γ=0.635 J/m2. Opposite gliding of the left half lattice of a
CTB structure but can result in a new and high energy structure of γ=0.635 J/m2. Opposite gliding of the left half lattice of a 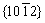 CTB by
CTB by  can also fully restore the original
can also fully restore the original 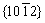 CTB structure after relaxation, accompanying with a left-shift of the twin boundary. The
CTB structure after relaxation, accompanying with a left-shift of the twin boundary. The  CTB is similar with the
CTB is similar with the  case: only the
case: only the  gliding can restore the
gliding can restore the  CTB structure with a left-shift of the twin boundary.
CTB structure with a left-shift of the twin boundary.

Fig. 2 Supercell model for  CTB in hcp Ti (a),
CTB in hcp Ti (a),  GTB (b) resulted from gliding of b=
GTB (b) resulted from gliding of b= from (a), restored
from (a), restored  CTB (c) after full relaxation of (b), accompanied with left-shift of twin boundary, pair of
CTB (c) after full relaxation of (b), accompanied with left-shift of twin boundary, pair of  GTBs (d) resulted from gliding on both sides of twin, and resulted widening of
GTBs (d) resulted from gliding on both sides of twin, and resulted widening of  CTB (e) after full relaxation of (d)
CTB (e) after full relaxation of (d)
We have manifested that all the  GTBs are high energy, metastable structures compared to their CTB counterparts. It is easy to deduce that simultaneous operation of opposite gliding on both sides of a
GTBs are high energy, metastable structures compared to their CTB counterparts. It is easy to deduce that simultaneous operation of opposite gliding on both sides of a  twin may cause a direct widening of the twin. This has been also manifested by calculations for a
twin may cause a direct widening of the twin. This has been also manifested by calculations for a  twin supercell (Figs. 2(d) and (e)) employing 80 Ti atoms and a 4×10×1 Γ-centered Monkhorst-Pack K-mesh for Brillouin-zone integration. A twin growth mechanism can be thus suggested as the continuous opposite gliding on both sides of the twin. We notice that the above gliding twin modes of
twin supercell (Figs. 2(d) and (e)) employing 80 Ti atoms and a 4×10×1 Γ-centered Monkhorst-Pack K-mesh for Brillouin-zone integration. A twin growth mechanism can be thus suggested as the continuous opposite gliding on both sides of the twin. We notice that the above gliding twin modes of 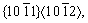
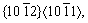 and
and  are not among common slip systems in hcp Ti, and one may thus expect that such gliding could be hardly induced by shear strains in real practice.
are not among common slip systems in hcp Ti, and one may thus expect that such gliding could be hardly induced by shear strains in real practice.
3.2 Roles of basal stacking faults (SFs)
Considering the important role of SFs in twin growth in cubic metals [41,42] and the relatively low formation energy of basal SFs in hcp Ti (~0.150 J/m2 for SF-I1, 0.260-0.350 J/m2 for SF-I2, ~0.360 J/m2 for SF-E [43,44]), we turned to explore the implications of basal SFs on GTB formation and the subsequent twin growth in hcp Ti. A basal edge dislocation with a unit Burgers vector can dissociate into two Shockley partial dislocations as 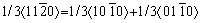 [45] (see Fig. 3(a)). Three basic types of basal SFs can result in Fig. 3(b): (1) extrinsic SF-E, having a stacking sequence of -(ABABCABAB)-, formed by inserting an extra basal plane, (2) intrinsic SF-I2, having a stacking sequence of -(ABABCACA)-, formed from a slip of
[45] (see Fig. 3(a)). Three basic types of basal SFs can result in Fig. 3(b): (1) extrinsic SF-E, having a stacking sequence of -(ABABCABAB)-, formed by inserting an extra basal plane, (2) intrinsic SF-I2, having a stacking sequence of -(ABABCACA)-, formed from a slip of  , and (3) intrinsic SF-I1, having a stacking sequence of -(ABABCBCB)-, formed by removing one basal layer followed by a slip of
, and (3) intrinsic SF-I1, having a stacking sequence of -(ABABCBCB)-, formed by removing one basal layer followed by a slip of  . Using a
. Using a  twin as an illustrative example, the
twin as an illustrative example, the  projections of these basal SFs and SF-impacted TBs are shown in Figs. 3(c-e). Introducing either an SF-E or an SF-I2 to the left side lattice (see Fig. 3(c) or (d)) led to a high energy TB structure after relaxation, while the TB with an SF-I1 in Fig. 3(e) reproduced exactly the
projections of these basal SFs and SF-impacted TBs are shown in Figs. 3(c-e). Introducing either an SF-E or an SF-I2 to the left side lattice (see Fig. 3(c) or (d)) led to a high energy TB structure after relaxation, while the TB with an SF-I1 in Fig. 3(e) reproduced exactly the  GTB structure of Fig. 2(b). This GTB can then favorably relax into the original, low energy CTB structure, accompanying with moving of the boundary (see Fig. 2). Such a structural correlation between SF-I1 and CTB was also predicted for
GTB structure of Fig. 2(b). This GTB can then favorably relax into the original, low energy CTB structure, accompanying with moving of the boundary (see Fig. 2). Such a structural correlation between SF-I1 and CTB was also predicted for 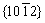 and
and  twins, which strongly suggests that SF-I1 could induce the gliding, to initiate twin widening and growth. Recall that the formation of SF-I1 involves partial dislocations on basal slip planes (see Fig. 3(b)). We can thus deduce that, on
twins, which strongly suggests that SF-I1 could induce the gliding, to initiate twin widening and growth. Recall that the formation of SF-I1 involves partial dislocations on basal slip planes (see Fig. 3(b)). We can thus deduce that, on  twin planes, by inducing basal SF-I1 (Fig. 3(b)), basal partial dislocations may cause the TB gliding in favor of the widening and growth of
twin planes, by inducing basal SF-I1 (Fig. 3(b)), basal partial dislocations may cause the TB gliding in favor of the widening and growth of  twins.
twins.
3.3 Twinning disconnections (TDs)
Figure 4 schematically reviews how basal SF-I1 can induce twin widening and growth. When basal SFs (SF-I1) reach a  twin from both sides, high energy GTB segments form in Fig. 4(b). Each segment relaxes back to a low energy CTB structure, causing the TB gliding and also leaving behind a pair of single-layer TDs. Clearly, the distance between I1 SFs determines the initial separation distance of the TD pairs, and the twin thus becomes serrated with TD steps in Fig. 4(c). Please note that this kind of TD steps have been observed very recently in Mg and its roles on twin boundary mobility have also been suggested [46]. Also, the single-layer TDs in Fig. 4(c) can be labelled as {0001}matrix//
twin from both sides, high energy GTB segments form in Fig. 4(b). Each segment relaxes back to a low energy CTB structure, causing the TB gliding and also leaving behind a pair of single-layer TDs. Clearly, the distance between I1 SFs determines the initial separation distance of the TD pairs, and the twin thus becomes serrated with TD steps in Fig. 4(c). Please note that this kind of TD steps have been observed very recently in Mg and its roles on twin boundary mobility have also been suggested [46]. Also, the single-layer TDs in Fig. 4(c) can be labelled as {0001}matrix// twin basal-pyramidal (BPy) steps, where the basal plane {0001} of the matrix (the red lattice) is exactly parallel to the pyramidal plane
twin basal-pyramidal (BPy) steps, where the basal plane {0001} of the matrix (the red lattice) is exactly parallel to the pyramidal plane  of the twin (the blue lattice). It can be naturally deduced that an accumulation of basal SFs could induce the pileup of TDs, leading to the formation of multiple wide BPy steps at the twin boundary. This has been confirmed in our pure Ti samples using HRTEM, as observed for
of the twin (the blue lattice). It can be naturally deduced that an accumulation of basal SFs could induce the pileup of TDs, leading to the formation of multiple wide BPy steps at the twin boundary. This has been confirmed in our pure Ti samples using HRTEM, as observed for  twins under the zone axis of
twins under the zone axis of  in Fig. 5. The coherent
in Fig. 5. The coherent  twin boundaries and multiple wide BPy steps are marked using yellow and red dashed lines, respectively.
twin boundaries and multiple wide BPy steps are marked using yellow and red dashed lines, respectively.

Fig. 3 Schematic for basal edge dislocation dissociation into two Shockley partials (a), formation of basal SFs I1, I2, and E (b), SF-E (c), SF-I2 (d), and SF-I1 (e) impacted  CTBs (Blue atoms represent perfect matrix lattice, and black atoms represent SF-free segment of
CTBs (Blue atoms represent perfect matrix lattice, and black atoms represent SF-free segment of  CTB)
CTB)
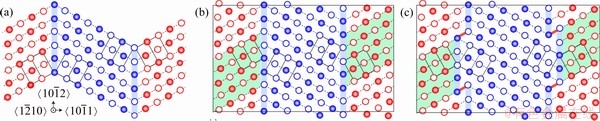
Fig. 4  twin embedded in hcp Ti matrix (a), supercell model for
twin embedded in hcp Ti matrix (a), supercell model for  twin with SF-I1 generated on both sides (b) and formation of TDs and twin widening (c) induced by SF-I1 after full relaxation from (b) (Green shadows highlight SF-I1 regions and red bars locate single-layer TD steps)
twin with SF-I1 generated on both sides (b) and formation of TDs and twin widening (c) induced by SF-I1 after full relaxation from (b) (Green shadows highlight SF-I1 regions and red bars locate single-layer TD steps)

Fig. 5 HRTEM images of  CTB with single, two-layer TD, or basal-pyramidal (BPy) step (Twin orientation relation was verified by the inserted Fast Fourier Transformation (FFT) pattern) (a) and serrated
CTB with single, two-layer TD, or basal-pyramidal (BPy) step (Twin orientation relation was verified by the inserted Fast Fourier Transformation (FFT) pattern) (a) and serrated  CTB featured with multiple, wider BPy steps (b)
CTB featured with multiple, wider BPy steps (b)
The formation energy of TD can be further predicted as
γTD=[ECTB+TD-(γCTBACTB+γSFASF+nμTi)]/(mATD) (2)
where ECTB+TD is the total energy of the supercell in Fig. 4(c); γCTB is the interface formation energy of the CTB as calculated using Eq. (1); γSF is the energy of SF per unit area, using 0.150 J/m2 [40,41]; ACTB, ASF, and ATD are the areas of the CTB, the SF, and the TD step, respectively; μTi is the chemical potential of Ti in its pure bulk; m is the total number of TDs in the supercell, i.e. m=4; n is the total number of Ti atoms in the supercell. The  twin supercell in Fig. 4(c) employed 128 Ti atoms, i.e. n=128. Brillouin-zone integration employed an 1×7×1 Γ-centered Monkhorst-Pack K-mesh. Using Eq. (2), the formation energy of the TD step was predicted to be 0.572 J/m2, much higher than that of the
twin supercell in Fig. 4(c) employed 128 Ti atoms, i.e. n=128. Brillouin-zone integration employed an 1×7×1 Γ-centered Monkhorst-Pack K-mesh. Using Eq. (2), the formation energy of the TD step was predicted to be 0.572 J/m2, much higher than that of the  CTB. This is simply due to the incoherent boundary feature of the TD (or BPy) steps as clearly seen in Fig. 4(c) and Fig. 5.
CTB. This is simply due to the incoherent boundary feature of the TD (or BPy) steps as clearly seen in Fig. 4(c) and Fig. 5.
3.4 Pinning effect of segregated solutes
In Ti-based alloys, the formation of TDs through the SF-I1 induced gliding could be affected by alloying solutes. We further evaluated the pinning effect of segregated solutes on the gliding of a  CTB by calculating the corresponding energy change as
CTB by calculating the corresponding energy change as
 (3)
(3)
where 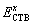 and
and  are the total energies of single solute x segregated CTB before and after the gliding, respectively. As the direct consequence of gliding, the CTB involves into its GTB counterpart that has a high energy and metastable structure. Various solutes that are commonly added into Ti alloys have been considered, including α-Ti stabilized solutes Al and Ge, β-Ti stabilized solutes Ag and V, and neutral solutes Y and Zr. Figure 6 shows possible segregation sites (sites 1-6) on the CTB plane and its neighbourhood. It should be noted that the relaxed structures and the corresponding total energies of the CTB and GTB are exactly identical. For all these solutes considered, the most favoured segregation site was found always to be Site 1 or Site 2 right on the CTB plane, corresponding to a segregation concentration of ~3.12%. Please note that Site 1 or Site 2 has one equivalent site within one stacking period along the CTB plane. Thus, using the supercell in Fig. 6, we can consider a higher segregation concentration of ~6.24%. The calculated △Eb results under the two segregation concentrations are compared in Table 2.
are the total energies of single solute x segregated CTB before and after the gliding, respectively. As the direct consequence of gliding, the CTB involves into its GTB counterpart that has a high energy and metastable structure. Various solutes that are commonly added into Ti alloys have been considered, including α-Ti stabilized solutes Al and Ge, β-Ti stabilized solutes Ag and V, and neutral solutes Y and Zr. Figure 6 shows possible segregation sites (sites 1-6) on the CTB plane and its neighbourhood. It should be noted that the relaxed structures and the corresponding total energies of the CTB and GTB are exactly identical. For all these solutes considered, the most favoured segregation site was found always to be Site 1 or Site 2 right on the CTB plane, corresponding to a segregation concentration of ~3.12%. Please note that Site 1 or Site 2 has one equivalent site within one stacking period along the CTB plane. Thus, using the supercell in Fig. 6, we can consider a higher segregation concentration of ~6.24%. The calculated △Eb results under the two segregation concentrations are compared in Table 2.

Fig. 6 Possible sites for solute segregation on  CTB plane or its first or second neighboring plane
CTB plane or its first or second neighboring plane
Table 2 Calculated energy change △Eb for gliding of
for gliding of  CTB with different segregation concentrations
CTB with different segregation concentrations

Higher positive △Eb values predict larger energy barriers for the twin gliding. It can be thus suggested from Table 2 that all the considered solute elements have a pinning effect on the  CTB gliding as compared to pure Ti. Among which, Zr and Al have relatively small influence. Ag and Ge show a fairly strong capability for pinning the twin boundary, followed by Y and V. Increasing the segregation concentration always enhances the pinning effect to different extents, but this trend is not obvious for Y. The solute pinning effect can certainly benefit in strengthening the matrix by stabilizing twin sizes [46,47]. In this regard, these phase-stabilizing solute elements in Ti could be re-classified into three different categories: strong twin-stabilizing solutes Ag and Ge, medium-strong twin-stabilizing solutes Y and V, and weak twin-stabilizing solutes Zr and Al. Our predicted pinning effects of various solutes on twin boundaries in Ti alloys await future experimental validation.
CTB gliding as compared to pure Ti. Among which, Zr and Al have relatively small influence. Ag and Ge show a fairly strong capability for pinning the twin boundary, followed by Y and V. Increasing the segregation concentration always enhances the pinning effect to different extents, but this trend is not obvious for Y. The solute pinning effect can certainly benefit in strengthening the matrix by stabilizing twin sizes [46,47]. In this regard, these phase-stabilizing solute elements in Ti could be re-classified into three different categories: strong twin-stabilizing solutes Ag and Ge, medium-strong twin-stabilizing solutes Y and V, and weak twin-stabilizing solutes Zr and Al. Our predicted pinning effects of various solutes on twin boundaries in Ti alloys await future experimental validation.
4 Conclusions
(1)  GTBs are metastable structures compared to their CTB counterparts and can be resulted from the gliding of CTBs. The simultaneous operation of opposite gliding on both sides of a twin may cause the twin widening. A new twin growth mechanism can be suggested through the continuous opposite gliding on both sides of the twin when subjected to shear strain.
GTBs are metastable structures compared to their CTB counterparts and can be resulted from the gliding of CTBs. The simultaneous operation of opposite gliding on both sides of a twin may cause the twin widening. A new twin growth mechanism can be suggested through the continuous opposite gliding on both sides of the twin when subjected to shear strain.
(2) Another new twin growth mechanism can be also suggested based on the CTB interaction with intrinsic basal SF-I1. Basal SFs can induce the gliding of CTBs, and further the formation and pileup of TDs on the CTB plane as observed in HRTEM, which can facilitate the twin widening and growth.
(3) Furthermore, solute segregation can also favourably affect the TB gliding. New strengthening strategies can be thus suggested for Ti alloys by direct pinning twin boundaries using strong twin-stabilizing solute elements, such as Ag and Ge.
Acknowledgments
The authors would like to thank the financial support from the National MCF Energy R & D Program of China (2018YFE0306100), the National Natural Science Foundation of China (51971249) and the State Key Laboratory for Powder Metallurgy, Central South University, Changsha, China. The computational resource at the High Performance Computing Center of Central South University is also gratefully acknowledged.
References
[1] GONG M Y, HIRTH J P, LIU Y, SHEN Y, WANG J. Interface structures and twinning mechanisms of  twins in hexagonal metals [J]. Materials Research Letters, 2017, 5(7): 449-464.
twins in hexagonal metals [J]. Materials Research Letters, 2017, 5(7): 449-464.
[2] WANG Y M, SANSOZ F, LAGRANGE T, OTT R T, MARIAN J, BARBEE T W Jr, HAMZA A V. Defective twin boundaries in nanotwinned metals [J]. Nature Materials, 2013, 12(8): 697-702.
[3] WANG J W, CAI X B, SHI R, WU Z F, WANG W J, LONG G, TANG Y J, CAI N D, OUYANG W K, GENG P, CHANDRASHEKAR B N, AMINI A, WANG N, CHENG C. Twin defect derived growth of atomically thin MoS2 dendrites [J]. ACS Nano, 2018, 12(1): 635-643.
[4] FULLMAN R L, FISHER J C. Formation of annealing twins during grain growth [J]. Journal of Applied Physics, 1951, 22(11): 1350-1355.
[5] HUANG C X, WANG K, WU S D, ZHANG Z F, LI G Y, LI S. Deformation twinning in polycrystalline copper at room temperature and low strain rate [J]. Acta Materialia, 2006, 54(3): 655-665.
[6] HIRTH J P, WANG J, TOME C N. Disconnections and other defects associated with twin interfaces [J]. Progress in Materials Science, 2016, 83: 417-471.
[7] CHRISTIAN J W, MAHAJAN S. Deformation twinning [J]. Progress in Materials Science, 1995, 39(1-2): 1-157.
[8] AVEDESIAN M M, BAKER H. Magnesium and magnesium alloys [M]. Ohio: Materials Park, 1999.
[9] HIRTH J P, POND R C. Steps, dislocations and disconnections as interface defects relating to structure and phase transformations [J]. Acta Materialia, 1996, 44(12): 4749-4763.
[10] WANG J, LIU L, TOME C N, MAO S X, GONG S K. Twinning and de-twinning via glide and climb of twinning dislocations along serrated coherent twin boundaries in hexagonal-close-packed metals [J]. Materials Research Letters, 2013, 1(2): 81-88.
[11] WANG J, BEYERLEIN I J, HIRTH J P, TOME C N. Twinning dislocations on  and
and  planes in hexagonal close-packed crystals [J]. Acta Materialia, 2011, 59(10): 3990-4001.
planes in hexagonal close-packed crystals [J]. Acta Materialia, 2011, 59(10): 3990-4001.
[12] WANG J, HIRTH J P, TOME C N.  twinning nucleation mechanisms in hexagonal-close-packed crystals [J]. Acta Materialia, 2009, 57(18): 5521-5530.
twinning nucleation mechanisms in hexagonal-close-packed crystals [J]. Acta Materialia, 2009, 57(18): 5521-5530.
[13] THOMPSON N, MILLARD D J. XXXVIII. Twin formation, in cadmium [J]. Philosophical Magazine, 2010, 43(339): 422-440.
[14] SERRA A, BACON D J. A new model for 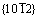 twin growth in hcp metals [J]. Philosophical Magazine A, 2006, 73(2): 333-343.
twin growth in hcp metals [J]. Philosophical Magazine A, 2006, 73(2): 333-343.
[15] MENDELSON S. Zonal dislocations and twin lamellae in h.c.p. metals [J]. Materials Science and Engineering, 1969, 4(4): 231-242.
[16] SERRA A, BACON D J. On the generation of twinning dislocations in hcp twin boundaries [J]. Materials Science Forum, 1996, 207: 553-556.
[17] BRAISAZ T. High-resolution electron microscopy study of the 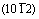 twin and defects analysis in deformed polycrystalline alpha titanium [J]. Philosophical Magazine Letters, 2010, 74(5): 331-338.
twin and defects analysis in deformed polycrystalline alpha titanium [J]. Philosophical Magazine Letters, 2010, 74(5): 331-338.
[18] BRAISAZ T, RUTERANA P, NOUET G. Twin tip defects related to the nucleation and growth mechanisms of the twin 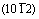 in zinc characterized by high-resolution electron microscopy [J]. Philosophical Magazine A, 1997, 76(1): 63-84.
in zinc characterized by high-resolution electron microscopy [J]. Philosophical Magazine A, 1997, 76(1): 63-84.
[19] LI B, MA E. Atomic shuffling dominated mechanism for deformation twinning in magnesium [J]. Physical Review Letters, 2009, 103(3): 035503.
[20] LI B, MA E. Zonal dislocations mediating  twinning in magnesium [J]. Acta Materialia, 2009, 57(6): 1734-1743.
twinning in magnesium [J]. Acta Materialia, 2009, 57(6): 1734-1743.
[21] KUMAR A, WANG J, TOME C N. First-principles study of energy and atomic solubility of twinning-associated boundaries in hexagonal metals [J]. Acta Materialia, 2015, 85: 144-154.
[22] BHATIA M A, SOLANKI K N. Energetics of vacancy segregation to symmetric tilt grain boundaries in hexagonal closed pack materials [J]. Journal of Applied Physics, 2013, 114(24): 244309.
[23] WANG J, BEYERLEIN I J. Atomic structures of symmetric tilt grain boundaries in hexagonal close packed (hcp) crystals [J]. Modelling and Simulation in Materials Science and Engineering, 2012, 20(2): 024002.
[24] ZHANG J, DOU Y C, ZHENG Y. Twin-boundary segregation energies and solute-diffusion activation enthalpies in Mg-based binary systems: A first-principles study [J]. Scripta Materialia, 2014, 80: 17-20.
[25] TSURU T, SOMEKAWA H, CHRZAN D C. Interfacial segregation and fracture in Mg-based binary alloys: Experimental and first-principles perspective [J]. Acta Materialia, 2018, 151: 78-86.
[26] HAGEGE S, MORI M, ISHIDA Y. Computer simulation of the 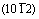 twin atomic structure in HCP metals [J]. Le Journal de Physique Colloques, 1990, 51(C1): C1-161- C1-166.
twin atomic structure in HCP metals [J]. Le Journal de Physique Colloques, 1990, 51(C1): C1-161- C1-166.
[27] BRAISAZ T, RUTERANA P, LEBOUVIER B, NOUET G. Atomic structure analysis of the 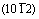 twin in zinc by HREM and energetical calculations [J]. Physica Status Solidi B—Basic Solid State Physics, 1995, 191(2): 267-281.
twin in zinc by HREM and energetical calculations [J]. Physica Status Solidi B—Basic Solid State Physics, 1995, 191(2): 267-281.
[28] MORRIS J R, YE Y Y, YOO M H. First-principles examination of the 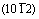 twin boundary in hcp metals [J]. Philosophical Magazine, 2005, 85(2-3): 233-238.
twin boundary in hcp metals [J]. Philosophical Magazine, 2005, 85(2-3): 233-238.
[29] WANG Y, CHEN L Q, LIU Z K, MATHAUDHU S N. First-principles calculations of twin-boundary and stacking- fault energies in magnesium [J]. Scripta Materialia, 2010, 62(9): 646-649.
[30] PEI Z R, ZHANG X, HICKEL T, FRIAK M, SANDLOBES S, DUTTA B, NEUGEBAUER J. Atomic structures of twin boundaries in hexagonal close-packed metallic crystals with particular focus on Mg [J]. NPJ Computational Materials, 2017, 3(1): 6.
[31] WANG C, WANG H Y, HUANG T L, XUE X N, QIU F, JIANG Q C. Generalized-stacking-fault energy and twin- boundary energy of hexagonal close-packed Au: A first- principles calculation [J]. Scientific Reports, 2015, 5: 10213.
[32] HIRTH J P, LOTHE J, MURA T. Theory of dislocations [J]. Journal of Applied Mechanics, 1983, 50: 476-477.
[33] ZHANG X Y, LI B, LIU Q. Non-equilibrium basal stacking faults in hexagonal close-packed metals [J]. Acta Materialia, 2015, 90: 140-150.
[34] WANG F, BARRETT C D, MCCABE R J, EL KADIRI H, CAPOLUNGO L, AGNEW S R. Dislocation induced twin growth and formation of basal stacking faults in 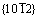 twins in pure Mg [J]. Acta Materialia, 2019, 165: 471-485.
twins in pure Mg [J]. Acta Materialia, 2019, 165: 471-485.
[35] OSTAPOVETS A, SERRA A, POND R C. Non-diffusional growth mechanism of I1 basal stacking-faults inside twins in hcp metals [J]. Scripta Materialia, 2019, 172: 149-153.
[36] OSTAPOVETS A, SERRA A. Slip dislocation and twin nucleation mechanisms in hcp metals [J]. Journal of Materials Science, 2016, 52(1): 533-540.
[37] KRESSE G, FURTHMüLLER J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set [J]. Computational Materials Science, 1996, 6(1): 15-50.
[38] KRESSE G, JOUBERT D. From ultrasoft pseudopotentials to the projector augmented-wave method [J]. Physical Review B, 1999, 59(3): 1758-1775.
[39] PERDEW J P, BURKE K, EMZEHOF M. Generalized gradient approximation made simple [J]. Physical Review Letters, 1996, 77(18): 3865-3868.
[40] YOO M H, MORRIS J R, HO K M, AGNEW S R. Nonbasal deformation modes of HCP metals and alloys: Role of dislocation source and mobility [J]. Metallurgical and Materials Transactions A—Physical Metallurgy and Materials Science, 2002, 33(3): 813-822.
[41] MAHAJAN S, CHIN G Y. Formation of deformation twins in f.c.c. crystals [J]. Acta Metallurgica, 1973, 21(10): 1353-1363.
[42] LI S Z, DING X D, DENG J K, LOOKMAN T, LI J, REN X B, SUN J, SAXENA A. Superelasticity in bcc nanowires by a reversible twinning mechanism [J]. Physical Review B, 2010, 82(20): 205435.
[43] BENOIT M, TARRAT N, MORILLO J. Density functional theory investigations of titanium γ-surfaces and stacking faults [J]. Modelling and Simulation in Materials Science and Engineering, 2013, 21(1): 015009.
[44] TARRAT N, BENOIT M, MORILLO J. Core structure of screw dislocations in hcp Ti: An ab initio DFT study [J]. International Journal of Materials Research, 2009, 100(3): 329-332.
[45] D HULL, BACON D J. Introduction to dislocations [M]. Amsterdam: Elsevier, 2011.
[46] ZHAO X, CHEN H, WILSON N, LIU Q, NIE J F. Direct observation and impact of co-segregated atoms in magnesium having multiple alloying elements [J]. Nature Communications, 2019, 10(1): 3243.
[47] NIE J F, ZHU Y M, LIU J Z, FANG X Y. Periodic segregation of solute atoms in fully coherent twin boundaries [J]. Science, 2013, 340(6135): 957-960.
钱 琦1*,刘正卿1*,江 勇1,2,王怡人1,安星龙2,宋 旼2
1. 中南大学 材料科学与工程学院,长沙 410083;
2. 中南大学 粉末冶金国家重点实验室,长沙 410083
摘 要:基于第一性原理计算研究密排六方结构钛中 共格孪晶界和滑移孪晶界的结构和能量,探讨滑移孪晶界的形成机理及其与孪晶生长的关系。结果表明,共格孪晶界与基面堆垛层错的相互作用可使共格孪晶界产生滑移,从而形成对应的滑移孪晶界。这种滑移最终能在孪晶界处形成一对单层孪生台阶,并恢复共格孪晶界的结构。孪生台阶的塞积可导致高分辨率透射电镜观察到的孪晶界上的台阶宽化,进一步促进孪晶的生长。此外,还评估多种合金化元素对孪晶界滑移的钉扎效应,为钛合金的强化设计提供指导。
共格孪晶界和滑移孪晶界的结构和能量,探讨滑移孪晶界的形成机理及其与孪晶生长的关系。结果表明,共格孪晶界与基面堆垛层错的相互作用可使共格孪晶界产生滑移,从而形成对应的滑移孪晶界。这种滑移最终能在孪晶界处形成一对单层孪生台阶,并恢复共格孪晶界的结构。孪生台阶的塞积可导致高分辨率透射电镜观察到的孪晶界上的台阶宽化,进一步促进孪晶的生长。此外,还评估多种合金化元素对孪晶界滑移的钉扎效应,为钛合金的强化设计提供指导。
关键词:孪晶界;层错;孪生台阶;孪晶生长;第一性原理
(Edited by Wei-ping CHEN)
Corresponding author: Yong JIANG, E-mail: yjiang@csu.edu.cn; Min SONG, E-mail: msong@csu.edu.cn
*Qi QIAN and Zheng-qing LIU contributed equally to this work
DOI: 10.1016/S1003-6326(21)65503-6
1003-6326/ 2021 The Nonferrous Metals Society of China. Published by Elsevier Ltd & Science Press
2021 The Nonferrous Metals Society of China. Published by Elsevier Ltd & Science Press

