J. Cent. South Univ. (2012) 19: 1475-1481

DOI: 10.1007/s11771-012-1164-5

Structural, thermodynamics and elastic properties of Mg₁₇Al₁₂, Al₂Y and Al₄Ba phases by first-principles calculations

HUANG Zhi-wei(黄志伟)¹, ZHAO Yu-hui(赵宇辉) ², HOU Hua(侯华)¹,

ZHAO Yu-hong(赵宇宏)¹, NIU Xiao-feng(牛晓峰)³, HAN Pei-de(韩培德)³

1. College of Materials Science and Engineering, North University of China, Taiyuan 030051, China;

2. Department of Mechanical and Electronic Engineering, Hebei College of Industry and Technology,

Shijiazhuang 050091, China;

3. College of Materials Science and Engineering, Taiyuan University of Technology, Taiyuan 030024, China

? Central South University Press and Springer-Verlag Berlin Heidelberg 2012

Abstract: Structural stabilities, thermodynamics stabilities, elastic properties and electronic structures of Mg₁₇Al₁₂, Al₂Y and Al₄Ba phases were analyzed by first-principles calculations with Castep and Dmol3 program based on the density functional theory. The calculated results of heat of formation indicate that Al₂Y phase has the strongest alloying ability. The calculated thermodynamic properties show that the thermal stability of these compounds gradually increases in the order of Mg₁₇Al₁₂, Al₂Y and Al₄Ba phases. Y or Ba addition to the Mg-Al alloys could improve the heat resistance. The calculated bulk modulus B, shear modulus G, elastic modulus E and Poisson ratio ν show that the adding Y or Ba to Mg-Al alloys could promote the brittleness and stiffness, and reduce tenacity and plasticity by forming Al₄Ba and Al₂Y phases. The calculated cohesive energy and density of state (DOS) show that Al₂Y has the strongest structural stability, then Al₄Ba and finally Mg₁₇Al₁₂. The calculated electronic structures show that Al₂Y has the strongest structure stability because of the strong ionic bonds and covalent bonds combined action.

Key words: Mg-Al alloys; thermodynamics properties; elastic properties; electronic structure; first-principles

1 Introduction

Magnesium alloys have received increasing attention in the last decade because of their great applications in automobile industry as casting products [1-2]. For Mg-Al alloys, β-Mg₁₇Al₁₂ is an essential phase that plays an important role in strengthening crystal boundary and controlling grain moving at high-temperature, whereas the softening of the phase at elevated temperature is detrimental to the creep property of the alloys. The use of these magnesium alloys in automobile industry is limited to non-critical parts because of its restricted mechanical properties. Y and Ba are two important additives used in Mg-Al alloys. Recent experimental investigations [3-4] showed that Y or Ba addition to the Mg-Al alloys had great effect on improving the heat resistance of the alloys by forming Al₂Y and Al₄Ba phases. But the alloying ability, thermodynamics stabilities and the structural stabilities of these compounds in Mg-Al alloys containing Y or Ba have not been well studied yet from the alloy energy viewpoint. To the best of our knowledge, LIU et al [5-6] reassessed the Al-Y phase diagram based on a critical literature review and experimental investigation. ZHAO et al [7] studied the microstructures and mechanical properties of AZ91 magnesium alloys with Y addition based on experimental method, and found that the ultimate tensile strength, yield strength and elongation of as-cast AZ91 magnesium alloys increase with Y addition. TAO et al [8] calculated the total energy and elastic properties of Laves phase Al₂Y by using ab-initio calculation. ZHANG et al [9] studied the effects of Ba on microstructure and mechanical properties of AZ91 magnesium alloys, and found that high temperature strength was significantly improved by forming Al₄Ba phase. However, no systematic theoretical study has been reported on structural stabilities, thermodynamics stabilities, mechanical properties and electronic structures of Mg₁₇Al₁₂, Al₂Y and Al₄Ba phases. In this work, the lattice constants, heat of formation, cohesive energy, thermodynamic properties, elastic properties and electronic structures of Mg₁₇Al₁₂, Al₂Y and Al₄Ba phases will be analyzed with first-principles methods.

2 Crystal structure and calculation details

Crystal structure parameters of Mg₁₇Al₁₂, Al₄Ba and Al₂Y phases are listed in Table 1 [10-12]. To calculate the energy, elastic constant and electronic structure, Cambridge sequential total energy package (CASTEP), a first-principles plane-wave pseudopotentials method based on density functional theory (DFT) was used in this work [13]. The ion–electron interaction was modeled by ultrasoft pseudo-potentials [14]. Generalized gradient approximation (GGA) [15] with the Perdew–Burke– Ernzerh (PBE) [16] of exchange–correlation function was used. The kinetic cut-off energy for plane waves was set as 330 eV [17]. The k-point separation in the Brillouin zone of the reciprocal space was 0.02 nm^-1, and the k-points were sampled by 6×6×6, 6×6×8, and 4×4×4 for Mg₁₇Al₁₂, Al₄Ba, and Al₂Y. To calculate the thermodynamic stabilities, Dmol3 program based on the density functional theory was used, relaxed through NVT molecular dynamics. The BLYP exchange–correlation function was adopted for GGA correction. All-electron Kohn–Sham wave functions were expanded in a double numerical basis with polarized orbital (DNP).

The calculated results of Al₂Y phase were compared with other experimental and theoretical analyses. It could be found that the calculated lattice parameter of     0.787 9 nm is in good agreement with the experimental value of 0.786 1 nm [18] and other theoretical value of 0.788 1 nm [19], with a difference within 0.23%. The calculated heat of formation for Al₂Y phase is    -52.32 kJ/mol, which is in good agreement with experimental result of -50.31 kJ/mol [20] and other theoretical value of -52.05 kJ/mol [19], with a deviation within 3.8%. All the results of the analysis indicate that the computational scheme utilized in this work is credible.

3 Results and discussion

3.1 Heat of formation and cohesive energy

Heats of formation (?H) of Mg₁₇Al₁₂, Al₄Ba and Al₂Y phases were calculated as follows [21]:

              (1)

where E_tot is the total energy of the unit cell; x and y refer to the numbers of Mg, Al, Y and Ba atoms, respectively. 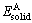 and  are the energies per Mg, Al, Y and Ba atom in the solid states. The calculated energies of Mg, Al, Y and Ba atoms for considered systems are   -977.836 4, -56.463 1, -1 052.582 4 and -699.304 5 eV, respectively.

The obtained heats of formation of Mg₁₇Al₁₂, Al₄Ba and Al₂Y phases calculated from Eq. (1) are presented in Fig. 1. It can be found that heats of formation of Mg₁₇Al₁₂, Al₄Ba and Al₂Y are -4.36, -25.01 and -52.32 kJ/mol. Heat of formation of Mg₁₇Al₁₂ is in good agreement with the corresponding calculated value of -3.281 kJ/mol [22] and -5.02 kJ/mol [23], confirming the reliability of the calculation methodology. Further analysis shows that the heat of formation of Mg₁₇Al₁₂, Al₄Ba and Al₂Y are all negative, which means that the structure of these phases can exist stably. Since the negative heats of formation of Mg₁₇Al₁₂, Al₄Ba and Al₂Y are gradually increased, it could be concluded that Al₂Y phase has the strongest alloying ability, then Al₄Ba and finally Mg₁₇Al₁₂.

The stability of crystal is determined by its cohesive energy [24]. Generally, the cohesive energy can be defined as the total energy released when isolated atoms combine into solid. Hence, the larger the absolute value is, the more stable the crystal structure is. In this work, the cohesive energies of Mg₁₇Al₁₂, Al₄Ba and Al₂Y phases are calculated as follows [25]:

            (2)

where E_coh is the total energy of the unit cell used in the present calculation; x and y refer to the numbers of Mg, Al, Y and Ba atoms in unit cell, respectively; 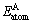 and  are the energies of the isolated Mg, Al, Y and Ba atoms in the free state, respectively. The calculated energies of Mg, Al, Y and Ba isolated atoms are -976.068 0, -52.738 4, -1047.890 4 and -697.385 8 eV, respectively.

Table 1 Crystal structure parameters of Mg₁₇Al₁₂, Al₂Y and Al₄Ba phases

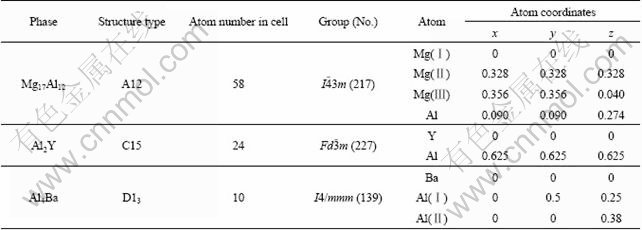
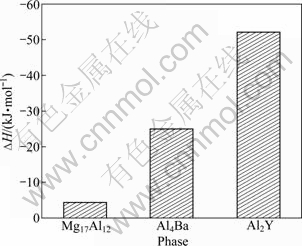
Fig. 1 Heat of formation (?H) of Mg₁₇Al₁₂, Al₄Ba and Al₂Y phases

The obtained cohesive energies of Mg₁₇Al₁₂, Al₄Ba and Al₂Y phases calculated from Eq. (2) are shown in Fig. 2. It is found that the cohesive energies of Mg₁₇Al₁₂, Al₄Ba and Al₂Y are -252.82, -349.18 and  -442.39 kJ/mol, respectively. Compared with other calculation values, it could be found that the cohesive energy of Mg₁₇Al₁₂ is in good agreement with the corresponding calculation value of -237.84 kJ/mol [22] and -224.66 kJ/mol [26]. Although cohesive energies from DFT are often notoriously bad, the accuracy of their calculations is encouraged by this relatively satisfactory result, confirming that the calculation results in this work are credible. Further analysis shows that Al₂Y phase has the most stable structure due to the highest absolute value of cohesive energy and Al₄Ba has relatively weaker structure stability, while the structure stability of Mg₁₇Al₁₂ is the worst due to the lowest absolute value of cohesive energy. All the results of the analysis indicate that the adding Y or Ba to Mg-Al alloys could promote the structure stability by forming Al₄Ba and Al₂Y phases.

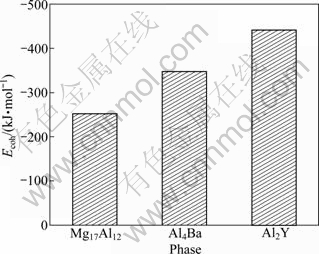
Fig. 2 Cohesive energy (E_coh) of Mg₁₇Al₁₂, Al₄Ba and Al₂Y phases

3.2 Thermodynamics stabilities

To study the effects of temperature on structure stabilities, thermodynamic properties of Mg₁₇Al₁₂, Al₂Y and Al₄Ba phases were calculated at different temperatures (298-573 K). Enthalpy (H) and Gibbs free energy (G) are calculated as follows [22]:

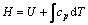                              (3)

                                 (4)

where T is the temperature; c_p is the heat capacity at the corresponding temperature; U is the heat of formation in the condition of 0 K and 1.01×10⁵ Pa; S is the entropy at the corresponding temperature.

The calculated results of the entropy (S), enthalpy (H) and Gibbs free energy (G) of Mg₁₇Al₁₂, Al₂Y and Al₄Ba are shown in Fig. 3. It is found that the values of entropy and enthalpy of three phases gradually increase with the elevated temperature, while the Gibbs free energy gradually decreases. By comparing the Gibbs free energy of three phases at the same temperature, the Gibbs free energy of Al₄Ba is the smallest, then Al₂Y, and finally Mg₁₇Al₁₂. The smaller the Gibbs free energy is, the better the thermal stability of compounds is [22]. Hence, the calculated results of the Gibbs free energy show that the thermal stability of these compounds gradually increases in the order of Mg₁₇Al₁₂, Al₂Y and Al₄Ba phases. The thermal stability of Al₂Y and Al₄Ba phases is better than Mg₁₇Al₁₂ phase and does not change with the elevated temperature, that is to say, Y or Ba addition to the Mg-Al alloys could improve the heat resistance. Thus, the experimental results [7, 9] of increasing the thermal stability of Mg-Al alloys with the addition of Y or Ba could be well explained from the view point of alloy energy.

3.3 Elastic properties

The elastic properties of Mg₁₇Al₁₂, Al₂Y and Al₄Ba phases, which are important for manufacturing Mg-Al alloys with Y or Ba addition, will be briefly discussed in this section. The calculated elastic constants for these phases in the present work are tabulated in Table 2.

Mg₁₇Al₁₂ and Al₂Y phases are composed of cubic crystals. The bulk modulus B and shear modulus G of Mg₁₇Al₁₂ and Al₂Y phases are calculated as follows [27]:

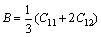                            (5)

                       (6)

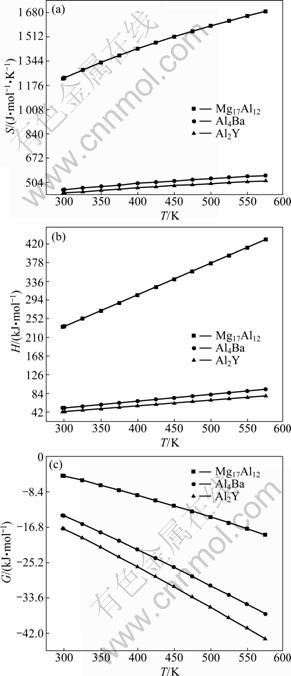
Fig. 3 Thermodynamic properties of Mg₁₇Al₁₂, Al₂Y and Al₄Ba: (a) Entropy (S); (b) Enthalpy (H); (c) Gibbs free energy (G)

Al₄Ba phase is composed of tetragonal crystals. The bulk modulus B and shear modulus G of Al₄Ba phase are calculated as follows [28]:

                    (7)

     (8)

The Poisson ratio ν and elastic modulus E of Mg₁₇Al₁₂, Al₂Y and Al₄Ba phases are deduced according to the following equations [27]:

                             (9)

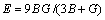                          (10)

The obtained mechanical parameters of Mg₁₇Al₁₂, Al₂Y and Al₄Ba phases are tabulated in Table 3. It could be found that C₁₂-C₄₄ values for Mg₁₇Al₁₂, Al₂Y and Al₄Ba phases are all negative. Generally, the ductility (brittleness) of crystal is determined by its C₁₂-C₄₄ values [24]. If the value is positive, it shows polycrystalline phases with ductile behavior; otherwise, it is brittle. Hence, Mg₁₇Al₁₂, Al₂Y and Al₄Ba phases are thought as brittle phases. DELLEY [29] introduced the ratio of shear modulus to bulk modulus (G/B) of polycrystalline phases to predict the brittle and ductile behavior of materials. The critical value, which separates ductility from brittleness, is about 0.57. When G/B is smaller than 0.57, the materials are ductile; when G/B is larger than 0.57, the materials are brittle. From Table 3, it is found that Mg₁₇Al₁₂, Al₂Y and Al₄Ba phases are all brittle because the G/B is larger than 0.57, which is in good agreement with the previous (C₁₂-C₄₄) results. Further analysis shows that the calculated G/B for Mg₁₇Al₁₂ is the smallest, indicating that Mg₁₇Al₁₂ is of very poor brittleness among the three phases.

Table 2 Calculated elastic constants of Mg₁₇Al₁₂, Al₂Y and Al₄Ba phases

Table 3 Moduli of three phases derived by this work from elastic constants

Elastic modulus E is defined as the ratio between stress and strain, and it can be used to provide a measure of the stiffness of the solid. The larger the value of E is, the stiffer the material is. The calculated results in Table 3 indicate that the stiffness of Al₂Y is the largest, then Al₄Ba and finally Mg₁₇Al₁₂. The Poisson ratio ν could be quantified as the stability of the crystal against shear. The calculated results indicate that Al₄Ba shows the lowest tenacity due to the smallest value of Poisson ratio ν, and Al₂Y has lower tenacity than Mg₁₇Al₁₂ phase.

C₁₁-C₁₂ and elastic modulus E are also very significant for the mechanical properties of materials. The smaller the values of C₁₁-C₁₂ and elastic modulus E are, the better the plasticity is. The calculated results of Fig. 4 show that Mg₁₇Al₁₂ has the best plasticity, then Al₄Ba and finally Al₂Y.

3.4 Electronic structures

To reveal the nature of bonding interactions within Mg₁₇Al₁₂, Al₂Y and Al₄Ba phases and understand their structural stability mechanisms, the total and partial densities of states (DOS) of three compound crystal cells are calculated and compared, as shown in Fig. 5. From Fig. 5(a), it is found that the main bonding peaks of Mg₁₇Al₁₂ between -45 and -40 eV mainly originate from the contribution of valence electron numbers of Mg(p) orbits, and the main bonding peaks between -10 and   5 eV are the result of the bonding Al(s), Al(p) and Mg(s), Mg(p) orbits. From Fig. 5(b), the main bonding peaks of Al₂Y are located at three energy ranges. The peaks between -45 and -40 eV and between -25 and -20 eV are dominated by the valence electron numbers of Y(s) and Y(p) orbits. But the main bonding peaks between -10 and 10 eV are the contribution of Al(s), Al(p) and Y(d) orbits. From Fig. 5(c), the main bonding peaks of Al₄Ba are located at three energy ranges. The main bonding peaks between -30 and -25 eV mainly originate from the contribution of valence electron numbers of Ba(s) orbits, the peaks between -15 and -10 eV mainly originate from the contribution of valence electron numbers of Ba(p) orbits, while the contributions of valence electron between -10 and 10 eV are Al(s), Al(p) and Ba(s). Further comparison of total densities of states (DOS) of Mg₁₇Al₁₂, Al₂Y and Al₄Ba phases per atom near the Fermi level is performed, as shown in Fig. 5(d). It is found that the bonding electron number of Mg₁₇Al₁₂ is 2.422 15 between the Fermi level and -10 eV, which is smaller than 2.987 91 for Al₂Y and 2.801 37 for Al₄Ba, respectively. The smaller the bonding electron number is, the weaker the charge interaction is [22-23]. Hence, Al₂Y has the strongest structural stability, then Al₄Ba and finally Mg₁₇Al₁₂. The same result is obtained by cohesive energy analysis, confirming the conclusion from the electronic structure point of view. In Fig. 5, the s bands of Al atoms are overlapped with the p bands of Al atoms, illustrating s-p hybridization between Al atoms forming covalent bonding.

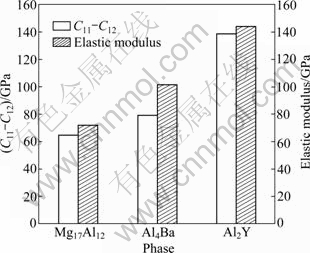
Fig. 4 Values of C₁₁-C₁₂ and elastic modulus E for Mg₁₇Al₁₂, Al₄Ba and Al₂Y phases

Fig. 5 Density of state of Mg₁₇Al₁₂, Al₂Y and Al₄Ba phases: (a) Mg₁₇Al₁₂; (b) Al₂Y; (c) Al₄Ba; (d) Total DOS per atom near Fermi level

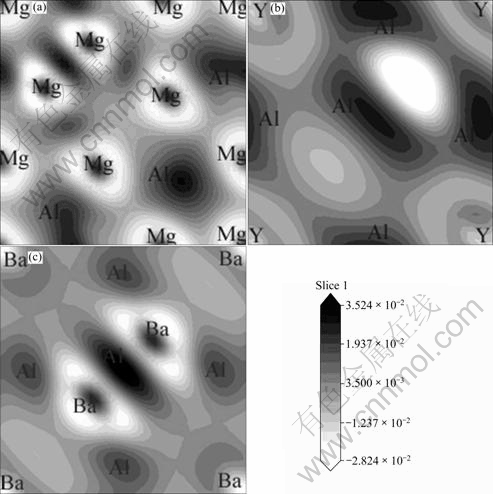
Fig. 6 Electronic charge density difference contour plots on (001) plane: (a) Mg₁₇Al₁₂; (b) Al₂Y; (c) Al₄Ba

The electron density difference maps, which are defined as the electron density difference between the isolated atoms and their bonding states, directly reflect their bonding nature, as shown in Fig. 6. The contour lines are plotted from -0.027 92 to 0.026 16 e/?³ with 0.013 52 e/?³ interval. The dark lines correspond to higher density region, and the gray lines correspond to lower density region. From Fig. 6(a), it is found that there are ionic Mg—Al bonds, covalent Al—Al bonds and metallic Mg—Mg bonds in Mg₁₇Al₁₂. Figure 6(b) also shows metallic Y—Y bonds, ionic Y—Al bonds, covalent Al—Al bonds in Al₂Y. In Fig. 6(c), metallic  Ba—Ba bonds, ionic Ba—Al bonds and covalent Al—Al bonds are found in Al₄Ba. According to analysis of densities of states (DOS) and the electronic charge density difference, Al₂Y has the strongest structure stability because of the strong ionic bonds and covalent bonds combined action.

4 Conclusions

1) The calculated heat of formation shows that Al₂Y phase has the strongest alloying ability. The calculated cohesive energy and density of state (DOS) show that Al₂Y has the strongest structural stability, then Al₄Ba and finally Mg₁₇Al₁₂.

2) The calculated thermodynamic properties show that the thermal stability of these compounds gradually increases in the order of Mg₁₇Al₁₂, Al₂Y and Al₄Ba phases. Y or Ba addition to the Mg-Al alloys can improve the heat resistance.

3) The calculated bulk modulus B, shear modulus G, elastic modulus E and Poisson ratio ν show that adding Y or Ba to Mg-Al alloys can promote the brittleness and stiffness, and reduce tenacity and plasticity by forming Al₄Ba and Al₂Y phases.

4) The calculated electronic structures show that Al₂Y has the strongest structure stability because of the strong ionic bonds and covalent bonds combined action.

References

[1] MORDIK B L, EBRET T. Magnesiums: Properties-applications- potential [J]. Mater Sci Eng A, 2001, 302(1): 37-45.

[2] LUO A, PEKGULERYUZ M O. Cast magnesium alloys for elevated temperature application [J]. J Mater Sci, 1994, 29(20): 5259-5271.

[3] ZHANG Jin-wang, XU Bing-she. Effects of Y on microstructure and mechanical properties of as-cast AZ31 magnesium alloy [J]. Journal of North University of China, 2009, 30(2): 192-196.

[4] LI Jin-feng, GENG Hao-ran, TENG Xin-ying. Effects of Ba on microstructure and mechanical properties of AZ91 magnesium alloy [J]. Hot Working Technology, 2005, 34(7): 5-7.

[5] LIU Shu-hong, DU Yong, CHEN Hai-lin. A thermodynamic reassessment of the Al-Y system [J]. Computer Coupling of Phase Diagrams and Thermochemistry, 2006, 30(3): 334-340.

[6] LIU Shu-hong, DU Yong, XU Hong-hui. Experimental investigation of the Al-Y phase diagram [J]. Journal of Alloys and Compounds, 2006, 414(1/2): 60-65.

[7] ZHAO Zu-de, CHEN Qiang, WANG Yan-bin. Microstructures and mechanical properties of AZ91D alloys with Y addition [J]. Materials Science and Engineering A, 2009, 515(1/2): 152-161.

[8] TAO Xiao-ma, OUYANG Yi-fang, LIU Hua-shan. Ab initio calculation of the total energy and elastic properties of Laves phase C15 Al 2 RE (RE=Sc, Y, La, Ce-Lu) [J]. Computational Materials Science, 2008, 44(2): 392-399.

[9] ZHANG Guo-ying, ZHNAG Hui, FANG Ge-liang, LI Yu-cai. A study on the mechanism of the influence of Bi, Sb alloying on microstructure and properties of AZ91 magnesium alloy [J]. Acta Physica Sinica, 2005, 54(11): 5288-5292.

[10] DU Wen-wen, SUN Yang-shan, MIN Xue-gang, XUE Feng, WU Deng-yun. Influence of Ca addition on valence electron structure of Mg₁₇Al₁₂ [J]. Chinese Nonferrous Metals, 2003, 13(6): 1247-1280.

[11] ANTON H, SCHMIDT P C. Theoretical investigations of the elastic constants in Caves phases [J]. Intermetallics, 1997, 5(6): 449- 465.

[12] SONG Y, GUO Z X, YANG R, LI D. First principles study of site substitution of ternary elements in NiAl [J]. Acta Mater, 2001, 49(9): 1647-1654.

[13] SHI Dong-min, WEN Bin, RODERICK M, YAO Shan, LI Ting-ju. First-principles studies of Al-Ni intermetallic compounds [J]. J Solid State Chem, 2009, 182(10): 2664-2669.

[14] FAGAN S B, MOTA R, BAIERLE R J, PAIVA G, SILA A J R D, FAZZIO A. Stability investigation and thermal behavior of a hypothetical silicon nanotube [J]. J Molecular Struct, 2001, 539(1): 101-106.

[15] PACK J D, MONKHORST H J. Special points for Brillouin-zone integrations-A reply[J]. Phys Rev B, 1977, 16(4/15): 1748-1749.

[16] PERDEW J P, BURKE K, ERNZERHOF M. Generalized gradient approximation made simple [J]. Phys Rev Lett, 1996, 77(18/28): 3865-3868.

[17] NYLEN J, GARCIA F J, MOSEL B D. Structure relationships, phase stability and bonding of compounds PdSn n (n=2, 3, 4) [J]. Solid State Sci, 2004, 6(1): 147-155.

[18] ZHANG L G, CHEN H M, DONG H Q. Thermodynamic description of the Al-Sb-Y system [J]. J Alloys Comps, 2009, 475(1/2): 233-237.

[19] OUYANG Yi-fang, TAO Xiao-ma, CHEN Hong-mei. First-principles calculations of mechanical and thermodynamic properties of the Laves C15-Mg₂RE (RE=La, Ce, Pr, Nd, Pm, Sm, Gd) [J].Computational Materials Science, 2009, 47(2): 297-301.

[20] JUNG W G, KLEPPA O J, TOPOR L. Standard molar enthalpies of formation of PdAl, PtAl, ScAl_1.78, YAl₂ and LaAl₂ [J].J Alloys Compds, 1991, 176(2): 309-318.

[21] CHEN Lü, PENG Ping, LI Gui-fa. First-principle calculation of point defective structures of B2-RuAl intermetallic compound [J]. Rare Metal Mater Eng, 2006, 35(7): 1065-1170.

[22] ZHOU D W, LIU J S, XU S H. Thermal stability and elastic properties of Mg₃Sb₂ and Mg₃Bi₂ phases from ?rst-principles calculations [J]. Physica B, 2010, 405(13): 2863-2868.

[23] ZHOU D W, LIU J S, LOU Y Z, ZHANG C H. Mechanism of Sb, Bi alloying on improving heat resistance properties of Mg-Al alloy[J]. Chinese Nonferrous Metals, 2008, 18(1): 118-125.

[24] FU C L, WANG X D, YE Y Y. Phase stability, bonding mechanism, and elastic constants of Mo₅Si₃ by first-principles calculation [J]. Intermetallics, 1999, 7(2): 179-184.

[25] DENG Yong-he, WANG Tao-fen, ZHANG Wei-bing. Crystal structure of Mg₃Pd from first-principles calculations [J]. Trans Nonferrous Met Soc China, 2008, 18(8): 416-420.

[26] VELIKOKHATNYI O I, KUMTA P N. First-principles studies on alloying and simpli?ed thermodynamic aqueouschemical stability of calcium-, zinc-, aluminum-, yttrium- and iron-doped magnesium alloys [J]. Acta Biomaterialia, 2010, 6(5): 1698-1704.

[27] LI C, HOE J L, WU P. Empirical correlation between melting temperature and cohesive energy of binary laves phases [J]. J Phys Chem Solids, 2003, 64(2): 201-212.

[28] KANOUN M.B, GOUMRI-SAID S, RESHAK A H. Theoretical study of mechanical, electronic, chemical bonding and optical properties of Ti₂SnC, Zr₂SnC, Hf₂SnC and Nb₂SnC [J]. Computational Materials Science, 2009, 47(2): 491-500.

[29] DELLEY B. Analytic energy derivatives in the numerical local- density-functional approach [J]. J Chem Phys, 1991, 94(11): 7245- 7250.

(Edited by HE Yun-bin)

Foundation item: Project(2011DFA50520) supported by the International Cooperation of Ministry of Science and Technology of China; Project(50975263) supported by the National Natural Science Foundation of China; Project(2010-78) supported by the Shanxi Provincial Foundation for Returned Scholars, China

Received date: 2011-07-15; Accepted date: 2011-12-29

Corresponding author: HOU Hua, Professor, PhD; Tel: +86-351-3557006; E-mail: houhua@263.net