


Trans. Nonferrous Met. Soc. China 22(2012) 1169-1175
Prediction of flow stress of Mg-Nd-Zn-Zr alloy during hot compression
WU Wen-xiang1, JIN Li1, DONG Jie1, DING Wen-jiang1,2
1. National Engineering Research Center of Light Alloy Net Forming, Shanghai Jiao Tong University,
Shanghai 200240, China;
2. State Key Laboratory of Metal Matrix Composite, Shanghai Jiao Tong University, Shanghai 200240, China
Received 3 June 2011; accepted 23 June 2011
Abstract: Isothermal hot compression tests were carried out on Mg-3.0Nd-0.2Zn-0.4Zr (mass fraction, %, NZ30K) alloy using a Gleeble-3500 thermo-simulation machine at temperatures ranging from 350 to 500℃ and strain rates from 0.001 to 1 s-1. A correction of flow stress for deformation heating at a high strain rate was carried out. Based on the corrected data for deformation heating, a hyperbolic sine constitutive equation was established. The constants in the constitutive equation of the hyperbolic sine form were determined as a function of strain. The flow stresses predicted by the developed equation agree well with the experimental results, which confirms that the developed constitutive equations can be used to predict the flow stress of NZ30K alloy during hot deformation.
Key words: NZ30K alloy? magnesium alloy; constitutive equation? flow stress? isothermal compression
1 Introduction
In the field of process modeling, finite element method (FEM) is used as a common tool to find out the optimum thermo-mechanical process parameters in metal forming processes, such as hot rolling, extrusion and forging. Constitutive equation which represents the flow behavior of materials is commonly used as input to the FEM code for simulating the material’s response under specified loading conditions [1]. Therefore, the prediction accuracy of the constitutive equation has a significant effect on the reliability of simulation results. In the past, a lot of work has been done to establish constitutive equation of materials from the experimental data [2-5] and the sine hyperbolic law in an Arrhenius type of equation has been extensively used to describe and predict high temperature flow behavior [6,7]. Various modifications to this equation have also been proposed to improve the prediction accuracy of flow stress. The influence of strain was incorporated in the constitutive equation considering the effect of strain on material constants to predict high temperature flow stress in modified 9Cr-1Mo (P91) steel, Al6061 and Ti-6Al-4V alloy [1,8,9]. A strain-dependent parameter was introduced in the sine hyperbolic constitutive equation to predict the flow stress in a wrought magnesium alloy Mg-Al4-Zn1 [10]. A revised sine-hyperbolic constitutive equation was developed considering strain and strain-rate compensation to predict the flow behavior in a 42CrMo steel and Ti-modified austenitic stainless steel [11,12]. Moreover, at a high strain rate (>1 s-1), the specimen temperature may change from the preset temperature during testing due to deformation heating, which can cause a noticeable change in the flow stress. Therefore, the measured data should be corrected for deformation heating before constitutive analysis [10,13].
Mg-3.0Nd-0.2Zn-0.4Zr (mass fraction, %; NZ30K) alloy has good specific strength and high corrosion resistance [14,15], and shows great potentials for application in aerospace and automotive industries. Industrial processes such as extrusion and forging for this material were carried out at a high deformation temperature [16,17]. Although many investigations have been carried out on the behaviors of NZ30K alloy, a thorough study on the hot deformation behavior of this alloy is still needed to optimize the thermo-mechanical process parameters. To date, very limited efforts have been made to understand and predict the flow behavior of NZ30K alloy during hot deformation. In this study, isothermal hot compression tests were carried out on NZ30K alloy. Based on the corrected data for deformation heating, a hyperbolic sine constitutive equation was determined to describe and predict the flow stress of NZ30K magnesium alloy during hot compression. The validity of the developed constitutive equations was also investigated over the entire experimental range.
2 Experimental
The material used in the present study was a cast NZ30K magnesium alloy with chemical composition of Mg-3.0Nd-0.2Zn-0.4Zr (mass fraction, %). Cylindrical specimens with 15 mm in height and 10 mm in diameter were machined from the DC-cast NZ30K ingot after homogenization treatment at 540℃ for 2 h for compression test. The isothermal hot compression tests were carried out on a Gleeble-3500 thermo-simulation machine at temperatures of 350-500℃ with strain rates of 0.001, 0.01, 0.1 and 1 s-1. To reduce the friction, graphite foils were put between the specimen and platens. Each specimen was heated to the deformation temperature at a rate of 10℃/s and held isothermally for 5 min before compression test, in order to obtain the heat balance. The specimens were deformed up to a true strain of 1.0 and then quenched in water immediately.
3 Results and discussion
3.1 Flow stress corrected for deformation heating
In hot deformation of metals, it is commonly accepted that the relationship between the stress, strain rate and temperature can be expressed as one of the following forms:
 (1)
(1)
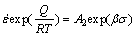 (2)
(2)
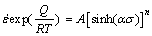 (3)
(3)
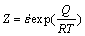 (4)
(4)
where A, A1, A2, n, n1, β and α are materials constants; α=β/n≈β/n1; Z is the Zener-Hollomon parameter; Q is the deformation activation energy; R is the mole gas constant; 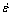 is the strain rate; T is the deformation temperature in Kelvin. The power law, Eq. (1), and the exponential law, Eq. (2), are applicable for a low stress and for a high stress, respectively. The hyperbolic sine law, Eq. (3), is a general form of constitutive equation suitable for stresses over a wide range.
is the strain rate; T is the deformation temperature in Kelvin. The power law, Eq. (1), and the exponential law, Eq. (2), are applicable for a low stress and for a high stress, respectively. The hyperbolic sine law, Eq. (3), is a general form of constitutive equation suitable for stresses over a wide range.
In order to determine a constitutive equation of flow stress, isothermal hot compression stress—strain data are usually employed. However, because of the deformation heat, the flow curves for high strain rate do not correspond to isothermal conditions. Figure 1 shows the measured specimen temperatures during hot compression test at temperatures of 350-500℃ for various strain rates. It can be seen from Fig. 1(a) that during the compression test at a pre-set temperature of 350℃ and a strain rate of 1 s-1, the specimen temperature rose from 350 to 369℃, at a strain of 0.45, and then decreased continuously as a result of heat loss through the anvils. At a lower strain rate of 0.1 s-1, the measured specimen temperature at this strain rate dropped a few degree under the pre-set temperature during the compression test. At an even lower strain rate of 0.01 s-1 or 0.001 s-1, there was enough time for heat loss and also for heat compensation by the external heat so that the measured specimen temperature remained stable throughout the test. Similar results can be obtained under temperatures of 400℃, 450℃ and 500℃ (Figs. 1(b)-(d)). From Fig. 1, it is obvious that increasing strain rate will increase the temperature variation, and the maximum temperature rise obtained at a strain rate of 1s-1 for various temperatures is greater than 5℃. Therefore, it is necessary to make a correction for deformation heating at the strain rate of 1 s-1 for determining a flow curve at a constant temperature. By contrast, the effects of temperature variation on the flow stress at a strain rate of 0.1, 0.01 or 0.001 s-1, which is less than 5℃, could be neglected.
The flow stress for strain rate of 1 s-1 was corrected using Eq. (2). Because there was no correlation of flow stress with strain in Eq. (2), the correction was made at various strains in the range of 0.1-1.0 with step size of 0.1. Taking the strain of 0.5 as an example, the correction of flow stress for deformation heat was made by plotting σ against T-1 for the strain rate of 1 s-1, as shown in Fig. 2, and then extrapolating back to the pre-set test temperatures.
Figure 3 shows the comparison between the corrected and measured flow curves. It can be seen that at high temperature above 400℃, the differences between the corrected and measured flow stresses are negligible. At low temperature of 350℃, however, the differences become significant, and the maximum difference in flow stress reaches as much as 12.6% at the strain of 0.5. It can be seen that at a given strain rate of 1 s-1, the flow stress increases with decreasing temperature. Under all the deformation conditions, the samples showed typical flow softening curves, including a peak followed by a gradual decrease in flow stress or a long steady state. Flow softening is a common characteristic of flow curves for many alloys deformed at a high temperature, and it is associated with microstructural evolution such as dynamic recrystallization (DRX), dynamic recovery (DRV) and dynamic coarsening of precipitates during hot deformation [18,19].

Fig. 1 Measured instantaneous specimen temperatures during compression tests with different strain rates at pre-set temperatures of 350℃ (a), 400℃ (b), 450℃ (c) and 500℃ (d)
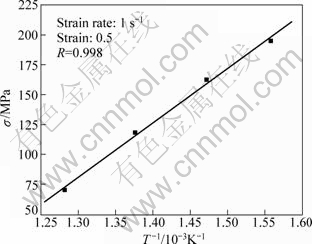
Fig. 2 Plot of σ against 1000/T at a strain of 0.5 and strain rate of 1 s-1
3.2 Determination of materials constants as functions of strain
It is assumed that the influence of strain on high temperature flow behavior is negligible and thereby not considered in Eqs. (1) to (4). However, at the lower hot working temperature and higher strain rate, the flow stress increases to a peak and then decreases with increasing strain (Fig. 3). Hence, compensation of strain should be taken into account in order to derive constitutive equations to accurately predict the flow stress. The influence of strain in the constitutive equation is incorporated by assuming that the material constants (i.e. α, n, Q and A) are polynomial functions of strains. The following takes the strain of 0.5 as an example to determine the material constants.
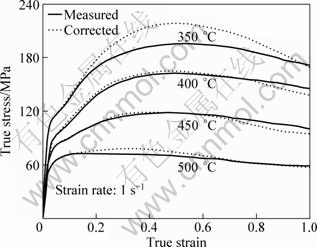
Fig. 3 Comparison between corrected and measured true stress—true strain curves at strain rate of 1 s-1
Taking the natural logarithm of both sides of Eqs. (1) and (2), respectively, gives,
 (5)
(5)
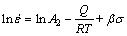 (6)
(6)
In the above equations, the slopes of the plots of ln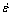 versus ln σ and ln
versus ln σ and ln 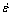 versus σ can be used to obtain the values of n1 and β, respectively, as shown in Fig. 4. Obviously, linear relationships are obtained in a double log plot at the temperatures of 450℃ and 500℃ (Fig. 4(a)) while the behavior is better represented by Eq. (6) at the temperatures of 350℃ and 400℃ (Fig. 4(b)). The exponent n1 rises from 3.34 at 500℃ to 3.52 at 450℃ and the power law breaks down at even lower temperatures where β decreases from 0.051 at 400℃ to 0.045 at 350℃. Therefore, a mean values of n1 and β are calculated as 3.43 and 0.048, respectively. Then α=β/n1= 0.014 MPa-1.
versus σ can be used to obtain the values of n1 and β, respectively, as shown in Fig. 4. Obviously, linear relationships are obtained in a double log plot at the temperatures of 450℃ and 500℃ (Fig. 4(a)) while the behavior is better represented by Eq. (6) at the temperatures of 350℃ and 400℃ (Fig. 4(b)). The exponent n1 rises from 3.34 at 500℃ to 3.52 at 450℃ and the power law breaks down at even lower temperatures where β decreases from 0.051 at 400℃ to 0.045 at 350℃. Therefore, a mean values of n1 and β are calculated as 3.43 and 0.048, respectively. Then α=β/n1= 0.014 MPa-1.
Taking the logarithm of Eq. (3) gives,
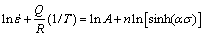 (7)
(7)
Differentiating Eq. (7) gives,
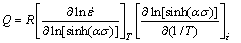 (8)
(8)
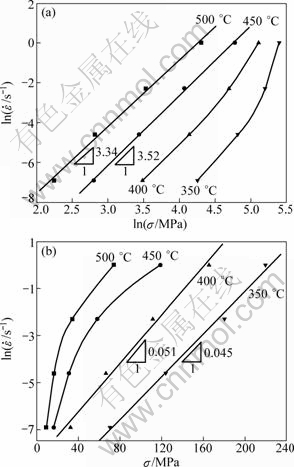
Fig. 4 Plots of ln 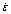 and ln σ (a) and ln
and ln σ (a) and ln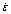 vs σ (b)
vs σ (b)
In this equation, the slopes of the plots of ln versus ln[sinh(ασ)] and ln[sinh(ασ)] versus 1/T can be used to obtain the value of Q. The relationship between flow stress (at the strain of 0.5) and strain rate, and deformation temperature are shown in Fig. 5. Therefore, Q is calculated as 184.99 kJ/mol.
versus ln[sinh(ασ)] and ln[sinh(ασ)] versus 1/T can be used to obtain the value of Q. The relationship between flow stress (at the strain of 0.5) and strain rate, and deformation temperature are shown in Fig. 5. Therefore, Q is calculated as 184.99 kJ/mol.
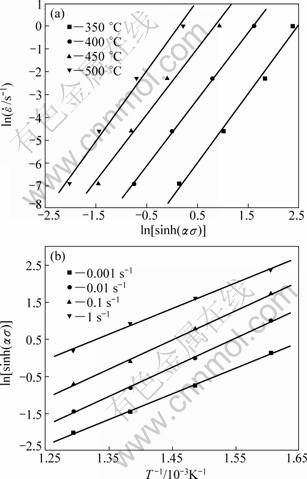
Fig. 5 Plots of ln 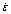 and ln[sinh(ασ)] (a) vs ln[sinh(ασ)] vs 1/T (b)
and ln[sinh(ασ)] (a) vs ln[sinh(ασ)] vs 1/T (b)
According to Eqs. (3) and (4), Z can be rewritten as:
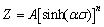 (9)
(9)
Taking the logarithm of both sides of Eq. (9) gives,
 (10)
(10)
Therefore, the plots of ln Z against ln[sinh(ασ)] can be used to obtain the value of n and ln A. The relationship between ln[sinh(ασ)] and lnZ is plotted in Fig. 6. From the slope of the fitting line, n and ln A can be calculated, respectively: n=2.977, ln A=28.34.
In the same way, the values of material constants (α, Q, A and n) of the constitutive equations were calculated under different deformation strains within the range of 0.1-0.9 and the interval of 0.1. The results are shown in Fig. 7. It is observed that α, n, Q and ln A show significant variation with strain. The solid lines in the figure represent the best fitted polynomial to these data. The material constants (i.e. α, n, Q and ln A) are the 5th polynomial function of strains, as shown in Eq. (11). The coefficients of the polynomial are listed in Table 1.
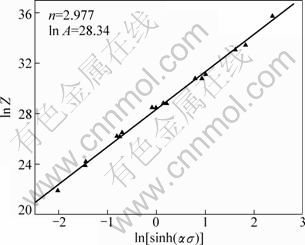
Fig. 6 Relationships between ln Z and ln[sinh(ασ)]
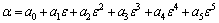 ,
,
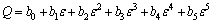 ,
,
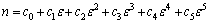 ,
,
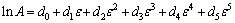 (11)
(11)
Table 1 Coefficients of polynomial for α, Q, n and ln A

3.3 Verification of constitutive equation
According to Eq. (9), the flow stress of the material at a particular strain can be expressed as:
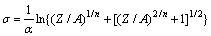 (12)
(12)
Figure 8 shows the comparison between the experimental and predicted flow stresses by Eq. (12). It could be observed that the predicted flow stress value from the developed constitutive equation agrees well with the experimental data throughout the entire strain rate and temperature ranges.
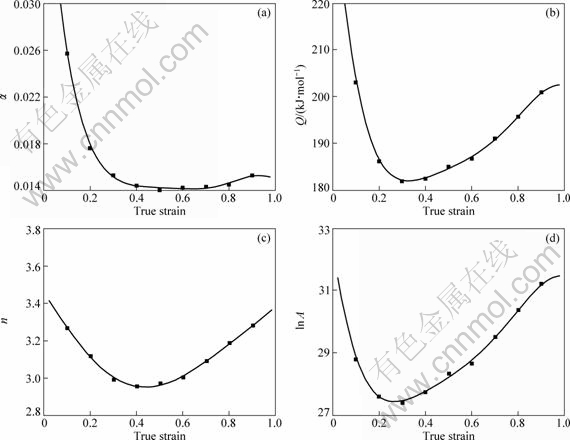
Fig. 7 Variation of α (a), Q (b), n (c) and ln A (d) with true strain
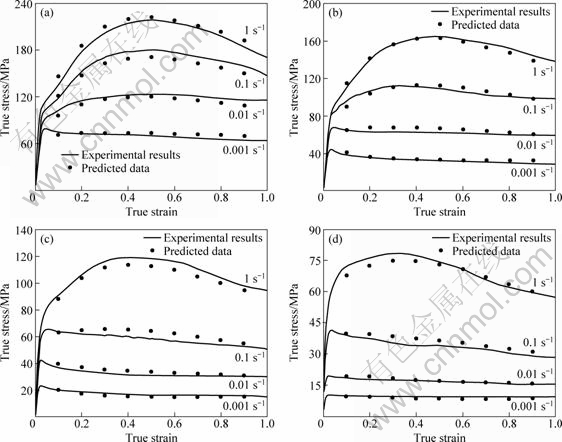
Fig. 8 Comparison between experimental and predicted flow stresses from constitutive equation at deformation temperature of 350℃ (a), 400℃ (b), 450℃ (c) and 500℃ (d)
The ability of this constitutive equation is evaluated by calculating root mean square error (RMSE) as follows:
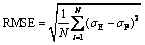 (13)
(13)
where σE is the experimental stress; σP is the predicted stress; N is the total number of data employed in the investigation. The value of RMSE for modeling of 16 flow curves by Eq. (13) was determined as 3.93 MPa, which reflects the good prediction capability of the developed constitutive equation.
4 Conclusions
1) A correction of flow stress for deformation heat at a high strain rate was carried out. Based on the corrected data for deformation heat, a hyperbolic sine constitutive equation was established. The constants in the constitutive equation were determined as a function of strain.
2) The developed hyperbolic sine constitutive equation was used to predict flow stress of NZ30K alloy during hot compression. A good correlation between experimental and predicted results has been obtained, and the value of root mean square error (RMSE) for modeling of 16 flow curves by the developed constitutive equation was determined as 3.93 MPa, which suggests that the developed constitutive equation is able to accurately predict the flow stress of NZ30K alloy during hot deformation.
References
[1] SAMANTARAY D, MANDAL S, BHADURI A K. Constitutive analysis to predict high-temperature flow stress in modified 9Cr-1Mo (P91) steel [J]. Materials and Design, 2010, 31: 981-984.
[2] SERAJZADEH S, TAHERI A K. Prediction of flow stress at hot working condition [J]. Mechanics Research Communications, 2003, 30: 87-93.
[3] TAKUDA H, MORISHITA T, KINOSHITA T, SHIRAKAWA N. Modelling of formula for flow stress of a magnesium alloy AZ31 sheet at elevated temperatures [J]. Journal of Materials Processing Technology, 2005, 164-165: 1258-1262.
[4] HE X M, YU Z Q, LAI X M. A method to predict flow stress considering dynamic recrystallization during hot deformation [J]. Computational Materials Science, 2008, 44: 760-764.
[5] MIRZADEH H, NAJAFIZADEH A. Flow stress prediction at hot working conditions [J]. Materials Science and Engineering A, 2010, 527: 1160-1164.
[6] McQUEEN H J, RYAN N D. Constitutive analysis in hot working [J]. Materials Science and Engineering A, 2002, 322: 43-63.
[7] ZHANG H, LI L X, YUAN D, PENG D S. Hot deformation behavior of the new Al-Mg-Si-Cu aluminium alloy during compresson at elevated temperatures [J]. Materials Characterization, 2007, 58: 168-173.
[8] GAN C L, XUE Y D, WANG M J. Prediction of the flow stress of Al 6061 at hot deformation conditions [J]. Materials Science and Engineering A, 2011, 528(12): 4199-4203.
[9] CAI J, LI F G, LIU T Y, CHEN B. Constitutive equations for elevated temperature flow stress of Ti-6Al-4V alloy considering the effect of strain [J]. Materials and Design, 2011, 32(3): 1144-1151.
[10] SLOOFF F A, ZHOU J, DUSZCZYK J. Constitutive analysis of wrought magnesium alloy Mg-Al4-Zn1 [J]. Scripta Materialia, 2007, 57: 759-762.
[11] LIN Y C, CHEN M S, ZHONG J. Constitutive modeling for elevated temperature flow behavior of 42CrMo steel [J]. Computational Materials Science, 2008, 42: 470-477.
[12] MANDAL S, RAKESH V, SIVAPRASAD P V. Constitutive equations to predict high temperature flow stress in a Ti-modified austenitic stainless steel [J]. Materials Science and Engineering A, 2009, 500: 114-121.
[13] LI L, ZHOU J, DUSZCZYK J. Determination of a constitutive relationship for AZ31B magnesium alloy and validation through comparison between simulated and real extrusion [J]. Journal of Materials Processing Technology, 2006, 172(3): 372-380.
[14] FU P H, PENG L M, JIANG H Y, CHANG J W, ZHAI C Q. Effects of heat treatments on the microstructures and mechanical properties of Mg-3Nd-0.2Zn-0.4Zr (wt.%) alloy [J]. Materials Science and Engineering A, 2008, 486: 183-192.
[15] CHANG J W, GUO X W, FU P H, PENG L M, DING W J. Effect of heat treatment on corrosion and electrochemical behaviour of Mg-3Nd-0.2Zn-0.4Zr (wt.%) alloy [J]. Electrochimica Acta, 2007, 52: 3160-3167.
[16] ZHENG X W, DONG J, XIANG Y Z. Formability, mechanical and corrosive properties of Mg-Nd-Zn-Zr magnesium alloy seamless tubes [J]. Materials and Design, 2010, 31: 1417-1422.
[17] ZHENG X W, DONG J, YIN D D. Forgeability and die-forging forming of direct chill casting Mg-Nd-Zn-Zr magnesium alloy [J]. Materials Science and Engineering A, 2010, 527: 3690-3694.
[18] LI L X, LOU Y, YANG L B. Flow stress behavior and deformation characteristics of Ti-3Al-5V-5Mo compressed at elevated temperatures [J]. Materials and Design, 2002, 23: 451-457.
[19] HUANG X D, ZHANG H, HAN Y, WU W X, CHEN J H. Hot deformation behavior of 2026 aluminum alloy during compression at elevated temperature [J]. Materials Science and Engineering A, 2010, 527: 485-490.
热压缩过程中Mg-Nd-Zn-Zr合金流变应力的预测
吴文祥1,靳 丽1,董 杰1,丁文江1,2
1. 上海交通大学 轻合金精密成型国家工程研究中心,上海 200240;
2. 上海交通大学 金属基复合材料国家重点实验室,上海 200240
摘 要:采用Gleeble-3500热模拟试验机对Mg-3.0Nd-0.2Zn-0.4Zr(质量百分数,NZ30K)合金进行等温热压缩试验,变形温度范围为350~500 ℃,应变速率范围为0.001~1 s-1。为消除变形热的影响,对高应变速率条件下的流变应力进行修正。利用修正后的流变应力数据,建立双曲正弦本构方程。双曲正弦本构方程中的常数可表达为应变的函数。利用建立的本构方程所预测的流变应力与实验结果吻合得较好,说明该本构方程可以用来预测NZ30K合金在热变形过程中的流变应力。
关键词:NZ30K合金;镁合金;本构方程;流变应力;等温压缩
(Edited by YANG Hua)
Foundation item: Project (2009AA033501) supported by High-tech Research and Development Program of China; Project (08DZ1150302) supported by the Science and Technology Commission Foundation Program of Shanghai Municipality, China; Project (0911) supported by Shanghai Automotive Industry Science and Technology Development Foundation, China
Corresponding author: JIN Li; Tel: +86-21-34203052; Fax: +86-21-34202794; E-mail: j_jinli@sjtu.edu.cn
DOI: 10.1016/S1003-6326(11)61301-0