2种切削顺序下TBM刀具破岩机理的数值研究
谭青1,徐孜军1,夏毅敏1, 2,张魁1, 2
(1. 中南大学 机电工程学院,湖南 长沙,410083;
2. 中南大学 现代复杂装备设计与极端制造教育部重点实验室,湖南 长沙,410083)
摘要:为研究切削顺序对全断面岩石掘进机(TBM)刀具破岩机理的影响,基于二维离散单元法,利用离散元仿真软件建立无围压条件下2把TBM刀具同时、顺次切削节理不发育岩石的仿真模型。在此基础上设计1组数值试验,模拟TBM刀具在不同刀间距下分别以这2种方式切割岩石时,岩石裂纹生成、扩展和岩石破碎块形成的全过程。最后,利用滚刀回转实验台对顺次加载方式下岩石的破碎模式进行验证。研究结果表明:切削顺序决定了岩石的破碎模式,但并不影响最优刀间距;当刀间距大于80 mm时,顺次加载方式的破岩效率不再高于同时加载方式下的破岩效率;在2种加载方式下,岩石应力场的分布基本对称;破碎块的形成与侧向裂纹的交汇密切相关。
关键词:切削顺序;TBM刀具;破碎模式;裂纹扩展;数值仿真
中图分类号:TP391.9;U455.3+1 文献标志码:A 文章编号:1672-7207(2012)03-0940-07
Numerical study on mode of breaking rock by TBM cutter in two cutting orders
TAN Qing1, XU Zi-jun1, XIA Yi-min1, 2, ZHANG Kui1, 2
(1. School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China;
2. Key Laboratory of Modern Complex Equipment Design and Extreme Manufacturing, Ministry of Education,Central South University, Changsha 410083, China)
Abstract: In order to research the effect of cutting orders on breaking mechanism of tunnel boring machine (TBM) cutter, based on the two-dimensional discrete element method, simulation models of breaking rock without joints by two TBM cutters in simultaneous and sequential orders under confining pressure-free were established using discrete element simulation software. A series of numerical experiments were designed and the whole process of production and propagation of crack and rock breaking were simulated in the conditions. Finally, an experiment was carried out on the rotatory cutting machine. The simulation results show that the cutter order determines the breaking mode, but the optimum cutter spacing is not affected. When the cutter spacing is larger than 80 mm, the efficiency of breaking rock in the sequential order is no longer higher than that in the simultaneous order. The distribution of the principal stress contour is almost symmetrical in two cutting orders. The formation of rock chip is directly bound up with the lateral cracks under the cutters propagation to each other and coalesce.
Key words: cutting order; tunnel boring machine cutter; breaking mode; crack propagation; numerical simulation
随着全断面岩石掘进机(TBM)在隧道施工中发挥的作用日趋重要,我国已把全断面岩石掘进机的自主研制纳入“十一五”规划中。该课题中一个极为重要的分支——在TBM刀具作用下岩石裂纹的生成与扩展规律研究,不但能够指导TBM刀具的研制,而且可以在不同地质条件下,为刀盘刀具的选型以及切削参数的拟定提供理论依据[1-2]。裂纹扩展问题是岩石力学研究领域中一个经典的课题。Hertz最早于19世纪80年代初定量地描述了在2个弹性体接触过程中,当侵入体载荷达到临界值时,在被侵入体内所产生的圆锥形裂纹及其向下的扩展问题。近年来,尹喜云等[3]针对动静组合加载破岩理论进行了研究,进一步获得了岩石裂纹真实的扩展模式。然而,实验研究具有一定的局限性。随着计算机性能的不断提高,数值模拟作为研究岩石材料破坏的有效手段日益被各国研究者所接受[4]。Liu等[5-6]建立了TBM刀具侵入岩石的有限元单元模型,成功模拟了岩石裂纹的生成与扩展过程。Su等[7]通过离散单元法模拟了岩石材料的微裂纹损伤演化过程。Wu等[8]将离散单元法应用于土压平衡盾构的沙土流动性问题,取得很好的效果。这些研究有助于了解TBM刀具的破岩机理,但一些关键的问题尚待进一步研究。例如,通过综合分析某型NFM、海瑞克、LOVAT盾构刀盘以及某型岩石掘进机刀盘的特点发现:复合土压平衡盾构刀盘上相邻2把正滚刀之间相位角的差值一般为60°,90°和180°;采用双刃滚刀的LOVAT盾构刀盘上滚刀之间的相位差还有一种是0°,即同时切削;而对于某型岩石掘进机的的刀盘来讲,滚刀布置的相位角从25.3°到178.6°不等[9-12]。因此,TBM刀具的切削顺序是刀具布置应予以考虑的重要问题。本文作者借助离散单元软件模拟岩石裂纹,研究刀具同时及顺次切削节理不发育岩石时岩石裂纹的生成、扩展规律,并结合滚刀回转实验验证数值模拟的可行性。
1 模型的建立及参数的选取
1.1 盘形滚刀破岩过程简化
TBM在施工中常遇到各种复杂的地质条件,难以建立全因素模型,因此,须对实际问题进行必要的简化。滚刀在掌子面上的破岩过程如图1所示,假定TBM在特定单一的地层下掘进,忽略地下水、温度场、围压及岩石裂隙、节理等因素的耦合作用,仅考虑TBM刀具破岩时垂直力的先后顺序对破岩机理的影响。本文模拟的顺次加载方式为:当前刀产生的裂纹相对稳定后,再对加载后刀的产生的裂纹进行研究。
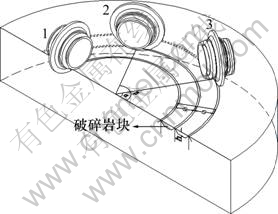
图1 滚刀破岩示意图
Fig.1 Diagram of disc cutter broken rock
模型示意图如图2所示,岩石长×宽为600 mm×600 mm,比例为1:1。TBM刀具与岩石接触面的厚度为15 mm,刀具对岩石的作用等效,应力载荷p均匀分布(p1表示前刀荷载,p2表示后刀荷载);Q为原岩围压,S为刀间距。岩石底边界约束 向速度自由度,岩石块划分成单元尺寸为5 mm的精细无限差分网格。设置局部阻尼系数为0.1,考虑重力的影响。
向速度自由度,岩石块划分成单元尺寸为5 mm的精细无限差分网格。设置局部阻尼系数为0.1,考虑重力的影响。
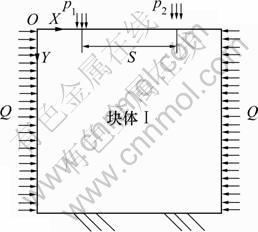
图2 计算模型示意图
Fig.2 Numerical simulation model
对于离散单元法,由于介质一开始就假定为离散块体的集合,故块与块之间没有变形协调的约束,除了边界条件外,只需满足平衡方程和本构方程即可。根据简化后的计算模型,得出平衡方程如下:
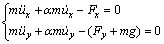 (1)
(1)
其中: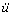 和
和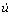 分别为u对离散时间步t的2阶和1阶导数,即系统的结点加速度和结点速度;
分别为u对离散时间步t的2阶和1阶导数,即系统的结点加速度和结点速度;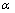 为块体的质量阻尼比例系数;Fx为x方向的外力,即围压Q;Fy为滚刀的垂直荷载即p,将其分成p1和p2分别加载到模型上。
为块体的质量阻尼比例系数;Fx为x方向的外力,即围压Q;Fy为滚刀的垂直荷载即p,将其分成p1和p2分别加载到模型上。
结合力学实验与文献手册综合分析,采用Mohr-Coulomb[13]准则作为其屈服准则,屈服函数如下:
 (2)
(2)
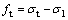 (3)
(3)
其中: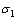 和
和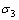 分别为最大和最小主应力;
分别为最大和最小主应力;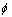 为摩擦角;c为凝聚力;
为摩擦角;c为凝聚力; 为岩石抗拉强度。
为岩石抗拉强度。
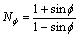 (4)
(4)
当岩体内某一点应力满足fs>0时,发生剪切破坏;当满足ft>0时,发生张拉破坏。
1.2 岩石参数及边界条件
通常,岩石的动态物理力学特性参数都与应变速率相关,但岩体的弹性模量和泊松比等参数随应变率的变化幅度很小,一般常用相应的静态参数表示。根据工程地质勘察报告和室内岩体力学实验[14],确定某砂岩的岩石特性参数,如表1所示。
为考察同时与顺次切削时岩石的破碎机理,测试条件进行如下变化:
(1) 加载方式为同时/顺次2种加载方式;
(2) 刀间距s为40,60,80和100 mm;
(3) Q=0 MPa,即无围压状态。
仿真过程中记录的参数如下:岩石的裂纹扩展过程;岩石破碎发生时刀具的临界应力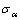 ;破碎块面积A;破碎块的宽度
;破碎块面积A;破碎块的宽度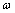 和厚度h;岩石的最大中间裂纹长度lmax与侧向裂纹的长度
和厚度h;岩石的最大中间裂纹长度lmax与侧向裂纹的长度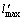 ;岩石的主应力云图等。
;岩石的主应力云图等。
表1 砂岩的材料参数
Table 1 Properties of sandstone

2 数值模拟结果及分析
由实验得到数据如表2所示。其中刀间距为40 mm同时加载时,在临界应力作用下仅在岩石表层形成很薄的一层封闭破碎区域,故破碎区面积可近似为0。
2.1 刀具的破岩效率
在这2种破岩方式下,刀具的临界应力随刀间距变化的曲线如图3(a)所示。从图3(a)可见:临界应力随刀间距的增加而增大;在相同刀间距下,顺次加载所需的临界应力高于同时加载方式,这意味着顺次加载的方式需要增加额外的应力以使岩石破碎。
图3(b)所示为刀间距与破岩效率的关系曲线。纵坐标为标准化切入率(TBM刀具相对于40 mm刀间距顺次切削作用时的相对切入率),横坐标为刀间距。从图3(b)可以看出,刀间距为小于80 mm范围时,随着刀间距的增大,2种破岩方式的破岩效率均增加;在同一刀间距下,顺次加载方式的破岩效率要比同时加载方式的高。80 mm刀间距为临界点,当刀间距大于或等于80 mm时,随着刀间距的增加,2种破岩方式的破岩效率均降低;在同一刀间距下,顺次加载方式的破岩效率反而比同时加载方式时的低。对于本文中的砂岩材料来说,2种加载方式下的最优刀间距均为80 mm,可见加载的方式并不影响最优刀间距。
表2 仿真结果
Table 2 Simulation results
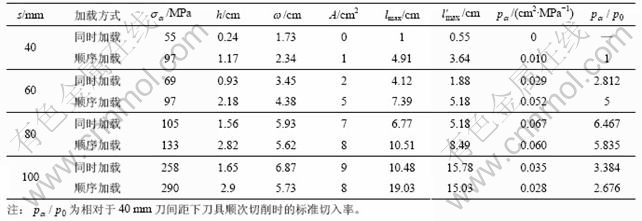
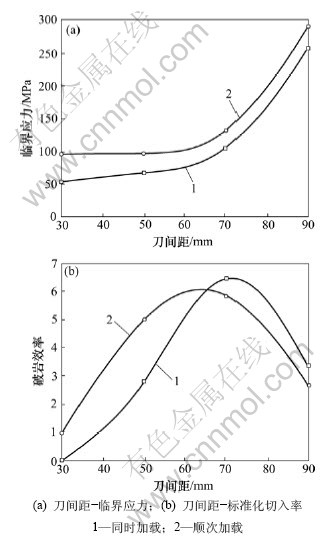
图3 刀间距与临界应力及破岩效率的关系曲线
Fig.3 Relationship among critical stress and normalized penetration rate and cutter space
2.2 刀具的破岩模式
选取最优刀间距(80 mm)下的破岩过程作为代表,分析裂纹演化规律。图4所示为同时加载方式下岩石裂纹的演化过程示意图。加载开始时,如图4(a)所示,在与刀具相接触的岩石自由面产生了细微的拉应力破坏区。加载前期,2个锥形压应力失效单元区域在刀刃下一定深度岩层处逐渐形成,而该深度以上至自由面处的岩体由于处在高围压条件下,尚未发生失效破坏,如图4(b)所示。随着侵深的增加,赫兹裂纹在锥形失效区前端产生,如图4(c)所示。同时,在锥形失效区内部,由于压应力过大产生了局部粉碎或显著塑性变形,开始在刀具下方出现1个袋状或球状的密实核。锥形失效区的边缘由于拉应力产生更多的微裂纹,并有向外扩散的趋势。刀刃继续侵入岩石,多条扩展速度相对较快的微裂纹形成了若干主要裂纹,即侧向裂纹和中间裂纹。同时,2把刀刃之间的岩石表面出现了拉应力失效区域,如图4(d)所示。侧向裂纹与中间裂纹继续扩展,但最为重要的是刀刃之间的侧向裂纹却在刀具的相互作用下改变了它们原来独立的扩展方向,趋于交汇,如图4(e)。岩石破碎于它们交汇的那一刻,也就是图4(f)所示的最终状态。这与Howarth和Bridge在实验室里观测到双压头作用下岩石裂纹生成规律是极为相似的[14]。
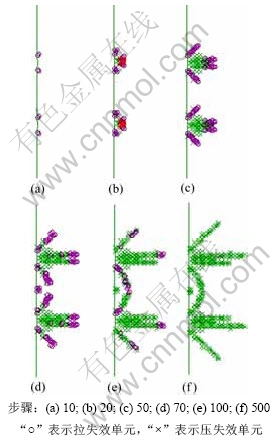
图4 刀间距为80 mm、同时切削时岩石裂纹的演化
Fig.4 Evolution process of crack in simultaneous order and cutter space is 80 mm
顺次加载方式下岩石裂纹的扩展过程如图5所示。前刀单独加载时岩石裂纹演化过程与上图4(a)~(c)所示的一致。当岩石裂纹趋于平衡时,后刀接着作用岩石,并产生了相似的锥形失效区,同时侧向与中间裂纹在拉应力作用下进一步扩展,如图5(d)所示。随着后刀切深的增加,其应力影响范围进一步加大,后刀加载的应力不仅促使自身侧向与中间裂纹的扩展,同时会对前刀形成的已有裂纹区域起到激活作用,表现为该区域部分裂纹分支重新产生拉应力失效区,并继续推动裂纹的进一步扩展,如图5(e)所示。后刀侧向裂纹继续沿原方向扩展,直至与前刀的侧向裂纹交汇形成破碎块,如图5(f)所示。

图5 刀间距为80 mm、顺次切削时岩石裂纹的演化
Fig.5 Evolution process of crack in the sequential order and cutter space is 80 mm
综上所述,在无围压条件下,2把TBM刀具同时和顺次切割节理不发育岩石时存在2种典型的裂纹演化过程。该过程决定了岩石的2种破坏形式,如图6所示。
2.3 裂纹长度与扩展能力
中间裂纹与侧向裂纹的长度随刀间距的变化规律如图7所示。由图7可知:无论哪种加载方式,裂纹均随着刀间距的增大而增大;在同一刀间距下,顺次加载时产生的中间裂纹长度明显比同时加载时产生的中间裂纹长;除100 mm刀间距外,顺次加载时产生的侧向裂纹长度比同时加载时产生的侧向裂纹长。
为衡量裂纹的扩展能力,计算单位应力作用下产生的岩石裂纹长度,并将其作为衡量裂纹扩展难易程度的重要依据。中间裂纹与侧向裂纹的扩展能力如图8所示。由图8可知:中间裂纹的扩展能力在最优刀间距时达到最大值,且顺次加载方式较易产生裂纹;但当刀间距达到100 mm时,顺次加载方式下的侧向裂纹扩展能力相对同时加载方式而言变弱。由于侧向裂纹的形成与破碎块有关,这从一个方面解释了100 mm刀间距时,同时加载的切入率比顺次加载时要高的原因。
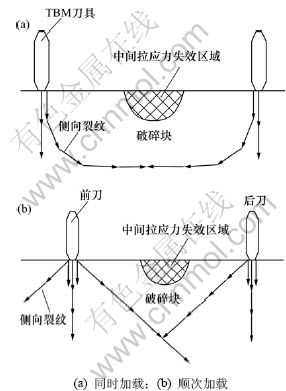
图6 2种典型的破碎模式
Fig.6 Two typical breaking modes
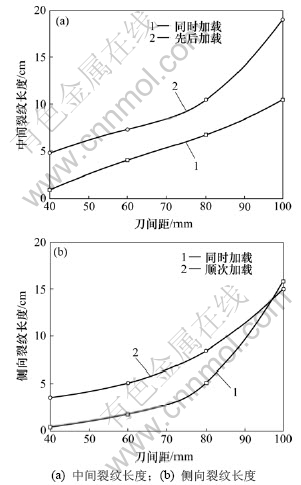
图7 岩石裂纹长度与刀间距关系曲线
Fig.7 Relationship between crack length and cutter space
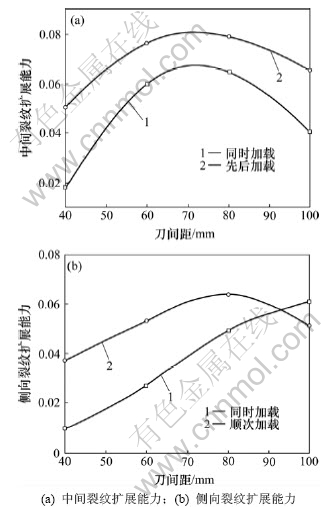
图8 裂纹扩展能力与刀间距的关系
Fig.8 Relationship between ability of crack expansion and cutter spacing
2.4 岩石的主应力云图
图9所示为2种不同加载方式下产生的主应力云图。可以看出:在这2种加载方式下,应力分布规律较相似:岩石应力场基本对称。在刀具的正下方应力较高,距自由面越远,应力降低直至为0 MPa;距离刀刃中心越远,应力越低。这一结论符合弹塑性力学中关于载荷作用于无限半平面上的应力分布规律。
2.5 结果分析
目前,国内外学者对滚刀破碎岩石切削特性的实验研究主要运用线性切割试验台,与实际切削工况有较大差异。针对大多数现有线切割实验中存在的不足,本课题组自行设计盾构回转组合刀具切削实验台,并开展了滚刀回转切削实验。该回转试验台可在不同切削速度、相位角和不同安装半径下进行切削实验。
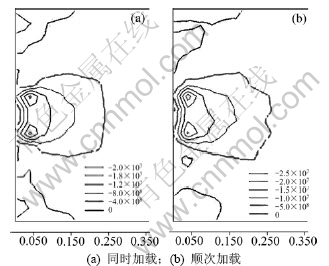
图9 岩石的主应力云图
Fig.9 Major principal stress contours of rock mass
本次实验取贯入度h=10 mm,回转角速度ω=2.6 r/min,刀间距s=54 mm。通过实验观测发现:破碎块的表面宽度基本一致,大约为54 mm,与滚刀刀间距相接近。破碎块左右边缘呈现坡形,且交汇成三角形截面,形状与顺次加载方式下破碎模式的类似。这表明:破碎块的形成与侧向裂纹的交汇贯穿密切相 关。仿真得到的破碎结果与实验现场所观测的结果基本一致。
3 结论
(1) 在2种切削顺序下,破碎岩石所需的临界应力随刀间距的增加而增大;在相同刀间距下,顺次加载所需的临界应力高于同时加载方式下的临界应力。对于砂岩材料来说,加载方式并不影响最优刀间距。当刀间距小于80 mm时,顺次加载方式的破岩效率比同时加载方式时的高;但刀间距继续增大时,破岩效率均下降,且顺次加载方式下降得更快。
(2) 在2种加载方式下,裂纹均随着刀间距的增大而增长。总体来看,顺次加载产生的中间/侧向裂纹比同时加载时产生的同类裂纹要长。顺次加载方式下较易产生裂纹,但当刀间距达到100 mm时,顺次加载方式下的侧向裂纹扩展能力相对同时加载方式而言变弱。
(3) 在2种加载方式下,应力的分布规律较相似,岩石应力场基本对称,使得滚刀作用下岩石裂纹成对称式扩展。
(4) 破碎块的形成与侧向裂纹的交汇密切相关。
参考文献:
[1] 宋克志, 李传明, 袁大军, 等. 盾构隧道施工盘形滚刀推力分布规律研究[J]. 岩石力学与工程学报, 2008, 27(A2): 3875-3881.
SONG Ke-zhi, LI Chuan-ming, YUAN Da-jun, et al. Study on distribution regularities of disc cutter thrust force for shield tunneling[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(A2): 3875-3881.
[2] 张厚美, 吴秀国, 曾伟华. 土压平衡式盾构掘进试验及掘进数学模型研究[J]. 岩石力学与工程学报, 2005, 24(A2): 5762-5766.
ZHANG Hou-mei, WU Xiu-guo, ZENG Wei-hua. Study on tunneling experiment and mathematical model of EPB shield[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(A2): 5762-5766.
[3] 尹喜云, 赵伏军. 动静组合加载作用下凿岩刀具失效的信息熵分析 [J]. 中南大学学报: 自然科学版, 2007, 38(4): 739-744.
YIN Xi-yun, ZHAO Fu-jun. Failure comentropy analysis of rock-drilling cutter under dynamic-static loading[J]. Journal of Central South University: Science and Technology, 2007, 38(4): 739-744.
[4] 苏利军, 孙金山, 卢文波. 基于颗粒流模型的TBM滚刀破岩过程数值模拟研究[J]. 岩土力学, 2009, 30(9): 2823-2829.
SU Li-jun, SUN Jin-shan, LU Wen-bo. Research on numerical simulation of rock fragmentation by TBM cutters using particle flow method[J]. Rock and Soil Mechanics, 2009, 30(9): 2823-2829.
[5] Liu H Y, Kou S Q, Lindqvist P A, Tang C A. Numerical simulation of the rock fragmentation process induced by indenters[J]. International Journal of Rock Mechanics and Mining Sciences, 2002, 4(39): 491-505.
[6] Liu H Y, Kou S Q, Lindqvist P A, Tang C A. Numerical modeling of the heterogeneous rock fracture process using various test techniques[J]. Rock Mechanics and Rock Engineering, 2007, 40(2): 107-144.
[7] Su O, N Ali Akcin. Numerical simulation of rock cutting using the discrete element method[J]. International Journal of Rock Mechanics and Mining Sciences, 2010, 48(3): 434-442.
[8] Wu L, Qu F Z. Discrete element simulation of mechanical characteristic of conditioned sands in earth pressure balance shield tunneling[J]. Journal of Central South University of Technology, 2009, 16(6): 1028-1033.
[9] Innaurato N, Oreste P. Theoretical study on the TBM tool-rock interaction[J]. Geotechnical and Geological Engineering, 1-9.
[10] 栾茂田, 张大林, 杨庆, 等. 有限覆盖无单元法在裂纹扩展数值分析问题中的应用[J]. 岩土工程学报, 2003, 25(5): 527-531.
LUAN Mao-tian, ZHANG Da-lin, YANG Qing, et al. Applications of the finite-cover element-free method in numerical analyses of crack-expansion[J]. Chinese Journal of Geotechnical Engineering, 2003, 25(5): 527-531.
[11] 宋天田, 周顺华. 复合地层条件下盾构刀盘设计研究[J]. 地下空间与工程学报, 2007, 3(3): 479-482.
S0NG Tian-tian, ZHOU Shun-hua. Design analysis on cutter head of shield machine in mixed strata[J]. Chinese Journal of Underground Space and Engineering, 2007, 3(3): 479-482.
[12] 宋克志, 王本福. 常见盾构刀盘型式及选用[J]. 隧道机械与施工技术, 2007, 6: 44-46.
SONG Ke-zhi, WANG Ben-fu. Common types of shield cutter wheel and selection[J]. Tunnel Machinery & Construction Technology, 2007, 6: 44-46.
[13] Itasca Consulting Group. UDEC reference manual[M]. 3rd ed. Minneapolis, Minnesota, USA, 1996: 30-62.
[14] 谭青, 张魁, 周子龙, 夏毅敏. 球齿滚刀作用下岩石裂纹的数值模拟与实验观测[J]. 岩石力学与工程学报, 2010, 29(1): 163-169.
TAN Qing, ZHANG Kui, ZHOU Zi-long, XIA Yi-min. Numerical simulation and experimental observation of rock cracks under action of spherical tooth hob cutter[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(1): 163-169.
(编辑 邓履翔)
收稿日期:2011-03-25;修回日期:2011-07-18
基金项目:国家自然科学基金资助项目(51074180);国家重点基础研究发展计划(“973”计划)资助项目(2007CB714002);中国博士后科学基金特别资助项目(201003519);湖南省科技重大专项资助项目(2010FJ1002);湖南省科技支撑计划资助项目(2010GK3073);中南大学研究生学位论文创新基金资助(2010ssxt170)
通信作者:谭青(1955-),男,江西南昌人,博士,教授,从事机械设计方法与理论、机械电子等方面的教学和科研工作;电话:13974870965;E-mail: jds-share@163.com