Trans. Nonferrous Met. Soc. China 26(2016) 1105-1111
Identification of constitutive model parameters for nickel aluminum bronze in machining
Zhong-tao FU1, Wen-yu YANG1, Si-qi ZENG2, Bu-peng GUO1, Shu-bing HU2
1. State Key Laboratory of Digital Manufacturing Equipment and Technology, School of Mechanical Science and Engineering, Huazhong University of Science and Technology, Wuhan 430074, China;
2. School of Materials Science and Engineering, Huazhong University of Science and Technology, Wuhan 430074, China
Received 27 May 2015; accepted 4 November 2015
Abstract: The material of nickel aluminum bronze (NAB) presents superior properties such as high strength, excellent wear resistance and stress corrosion resistance and is extensively used for marine propellers. In order to establish the constitutive relation of NAB under high strain rate condition, a new methodology was proposed to accurately identify the constitutive parameters of Johnson-Cook model in machining, combining SHPB tests, predictive cutting force model and orthogonal cutting experiment. Firstly, SHPB tests were carried out to obtain the true stress-strain curves at various temperatures and strain rates. Then, an objective function of the predictive and experimental flow stresses was set up, which put the identified parameters of SHPB tests as the initial value, and utilized the PSO algorithm to identify the constitutive parameters of NAB in machining. Finally, the identified parameters were verified to be sufficiently accurate by comparing the values of cutting forces calculated from the predictive model and FEM simulation.
Key words: nickel aluminum bronze; constitutive parameter; Johnson-Cook model; identification method
1 Introduction
As a copper-based alloy, nickel aluminum bronze (NAB) presents great advantages of high strength, and corrosion resistance, and thus is extensively used for marine propellers [1]. These optimum characteristics are mainly controlled by the thermo-mechanical behaviors in the cutting process. Many researches on NAB have mainly focused on microstructural evolution, corrosion properties [1-4], flow behavior under conventional material tests [5], and no regarding the plastic deformation behavior in machining. However, the material behavior encountered in conventional material tests could not be applied to metal cutting. Therefore, developing the accurate constitutive model and identifying the involved parameters are urgently needed to explain the material properties that influence the cutting process in both FEM simulation and analytical modelling of process variables.
Generally, for a constitutive model, the reliable flow stress data and the corresponding mathematical equation are required. Flow stress data are mainly obtained from three methods [6], i.e., material compression test [7-9], cutting experiment [10-13] and FEM [14-16]. SEDIGHI et al [7] investigated an approach in parametric identification of the high strain rate constitutive model using SHPB tests, and determined the model parameters by Levenberg-Marquardt method. PUJANA et al [10] proposed a reverse method to determine the constitutive model based on the variables in primary shear zone (PSZ) and second deformation zone (SDZ), and successfully identified the constitutive parameters of the steel 42CrMo4 and 20NiCrMo5. SHATLA et al [11] and SARTKULVANICH et al [12] used the orthogonal slot milling to obtain the variables in PSZ, and the constitutive parameters were derived from the iteration method by matching OXCUT output with the experimental cutting force. TOUNSI et al [15] and OZEL [16] obtained the constitutive parameters by matching FEM prediction with the measured cutting force in orthogonal cutting. However, these three methods have still some drawbacks. For SHPB method, strains were less than 1, the strain rates were not higher than 2×l04 s-1 [7], and the experimental equipment was relatively complex and high-cost. Cutting experiment method needed numerous cutting experiments and was time-consuming, and the identified results were not unique [12]. For FEM method, the adjustment of flow stress every time required many iterations to match predictive and measured value of cutting force, and each iteration needed more than 5 h [12].
Considering the previous review and the vast advantage of Johnson-Cook constitutive model in describing the material plastic flow behavior in machining [14,17], a methodology was proposed to identify the constitutive parameters of Johnson-Cook model for NAB material in machining. This was based on the combination of SHPB tests, predictive cutting force model and orthogonal cutting experiment. The method set up an objective function of the predictive and experimental flow stresses, put the identified values of SHPB tests as the initial value, and adopted the PSO algorithm to derive the constitutive parameters in machining. The identified parameters were verified by comparing the values of cutting forces obtained from the predictive model and FEM simulation.
2 Johnson-Cook constitutive model
The Johnson-Cook constitutive model is used widely in the simulation and analytical prediction of cutting process due to its high accuracy and mathematical simplicity, which can also describe the material behavior at high strains, high strain rates and high temperatures. So, it is chosen here to describe the plastic deformation behaviors of the material NAB, as given in Eq.:
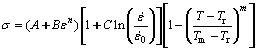 (1)
(1)
where σ is the flow stress, ε is the plastic strain, 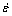 is the strain rate and T is the temperature. The material flow behaviors are defined by five parameters A, B, C, n and m, which are yield strength, strain hardening modulus, strain rate hardening coefficient, strain hardening exponent and thermal softening exponent, respectively. In addition,
is the strain rate and T is the temperature. The material flow behaviors are defined by five parameters A, B, C, n and m, which are yield strength, strain hardening modulus, strain rate hardening coefficient, strain hardening exponent and thermal softening exponent, respectively. In addition,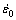 , Tr and Tm respectively represent reference strain rate, room temperature and melting temperature. For NAB, the melting temperature is 1058 °C.
, Tr and Tm respectively represent reference strain rate, room temperature and melting temperature. For NAB, the melting temperature is 1058 °C.
3 SHPB tests and results
The material used in the tests was NAB alloy, ZCuAl9Fe4Ni4Mn2, and its chemical composition (mass fraction) is: 80.30% Cu, 9.28% Al, 4.45% Fe, 4.24% Ni, 1.42% Mn, 0.0076% Zn, 0.011% Sn and 0.022% Pb, which is accordance with the standard GB1176-74 ISO484.
SHPB tests were used to obtain the true stress-strain curves at various temperatures and strain rates. In order to increase uniformity in deformation, the interfaces among the bars and specimen were lubricated with grease. Heating furnace was used to warm up the specimen and made the temperature reach the set value. The strain gages pasted on the bars can be used to measure and collect the strain signal. What is more, the initial diameter and height of the cylindrical specimens were 2 mm and 2 mm, respectively. And special treatment of the parallelism, flatness and roughness was made for the reliability of the experimental results.
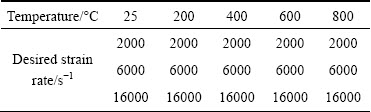
The designed temperatures and desired strain rates for SHPB tests are listed in Table 1. Since actual strain rate was not a constant, all the tests were repeated three times, and the data had good repeatability.
Table 1 Designed parameters of SHPB tests
The experimental results of SHPB tests are shown in Figs. 1 and 2. Figure 1 gave the true stress-strain curves of NAB at different temperatures and the same desired stain rate, while Fig. 2 represented ones at different desired stain rates and the same temperature. As seen in Figs. 1 and 2, the flow behaviors of NAB had the effect of obvious strain rate strengthening and thermal softening, i.e., at the same temperature, when strain rate increased, the flow stress increased. While the flow stress decreased with temperature rise under the same strain rate. This phenomenon can be attributed to: high strain rates forced the crystal movement at the grain boundary and resulted in the increase of flow stresses; at high temperatures, the thermal activation effect increased the dislocation slip plane and slip direction, and led to crystal plastic deformation easily, thus the flow stresses decreased along with the temperature rise.
Furthermore, quasi-static compression tests were also conducted using the Gleeble 3500 machine at a stain rate of 0.001 s-1 and room temperature. The cylindrical specimens used were 5 mm in diameter and 5 mm in height. Load and displacement of loading head were recorded. Then, true strain and stress of specimens could be calculated. The results of quasi-static compression test are shown in Fig. 3.
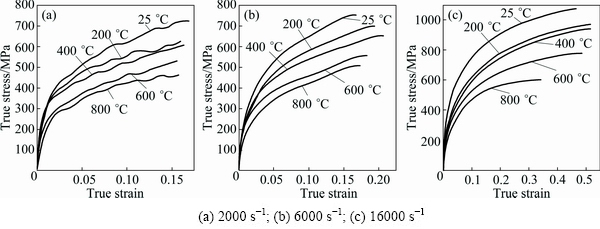
Fig. 1 True stress-strain curves of NAB at different temperatures and desired stain rates
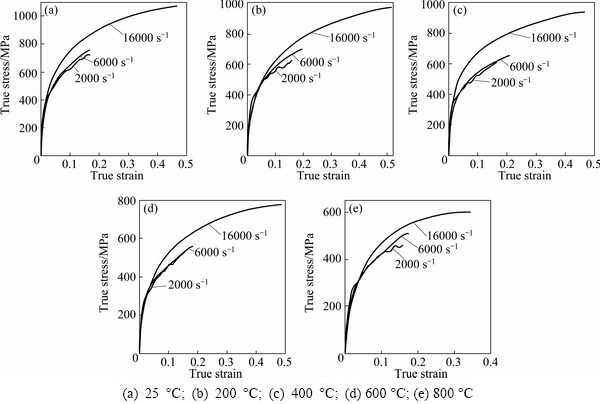
Fig. 2 True stress-strain curves of NAB at different stain rates and desired temperatures
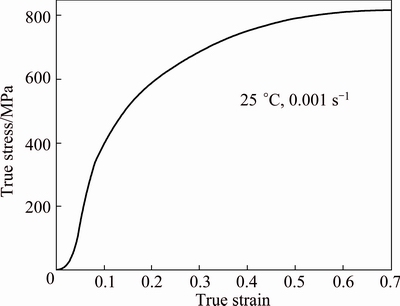
Fig. 3 True stress-strain curve of NAB in quasi-static compression test
Through eliminating the elastic deformation part of the experimental data, five unknown constitutive parameters in Eq. were derived by the fitting technology. Figure 3 reflected the true stress-strain curve in quasi-static compression test,i.e., 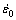 =0.001 s-1, Tr=298 K(25 °C), then Eq. (1) can be transformed as
=0.001 s-1, Tr=298 K(25 °C), then Eq. (1) can be transformed as
σ=A+Bεn (2)
where A is the yield stress which could be obtained from Fig. 3, i.e., A=295 MPa.
Using the nonlinear fitting method, we can get B=759.5 MPa, n=0.4757 (Fig. 4).
To input the flow stress data under the same strain rate and different temperatures (Fig. 2) into the material constitutive module of Deform 2D/3D, and keep A, B and n constant, parameters C and m could be obtained by fitting method automatically. Therefore, the constitutive parameters of Johnson-Cook model for NAB could be estimated to be A=295 MPa, B=759.5 MPa, n=0.4757, C=0.023 and m=1.24. Furthermore, the identified parameters were used to predict the stress-strain response. Figure 5 compared the experimental and predicted results. It could be seen that the predicted values agreed quite closely with the experimental data, which reflected the trend that the flow stress of NAB material varied with the change of strain, strain rate and temperature.
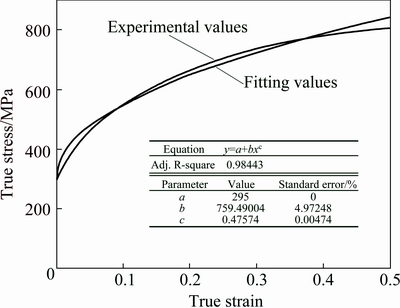
Fig. 4 Experimental and fitting results in quasi-static compression test
4 Identification of Johnson-Cook constitutive parameters in machining
In order to reflect the flow behavior of NAB material and obtain the accurate values of constitutive parameters in actual machining, the constitutive parameters, which were identified from the compression experiment in Section 3, were modified using the predictive model of cutting force and orthogonal cutting experiment. Figure 6 shows the flow chart of identifying Johnson-Cook constitutive parameters for NAB material in machining. The involved predictive model of cutting force could be used to predict cutting forces, cutting temperature, and the related status parameters in deformation zone, in which the input variables were workpiece material properties, tool geometry and cutting parameters. The detailed introduction should refer to Ref. [18].
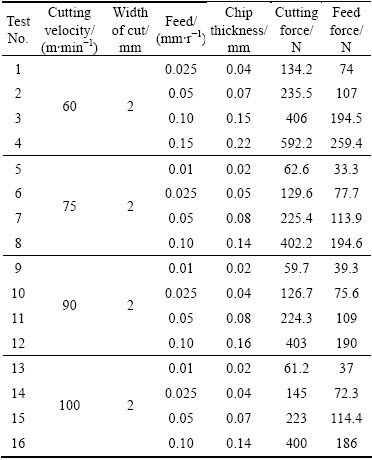
The experiment setup for orthogonal cutting is shown in Fig. 7. The uncoated inserts referenced Sandvik Coromant TNMG 160404-QM were used to cut the NAB tube with the following dimensions: inner diameter 50 mm, wall thickness 2 mm and length 200 mm. The rake angle was -6° and the relief angle was 0°. The radius of cutting edge was too small that could be regarded to be perfectly sharp. The cutting parameters were designed for 16 sets. To ensure the effectiveness of experimental results, each cutting experiment was repeated three times, and each cutting process lasted for 10-30 s. Table 2 shows the designed parameters and experimental results.
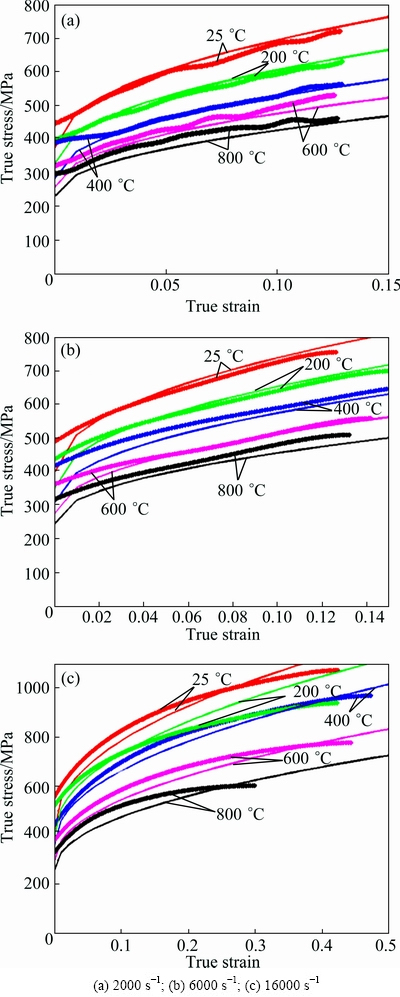
Fig. 5 Comparison of flow data obtained from experimental (bold dot line) and predicted (fine line) results at different strain rates
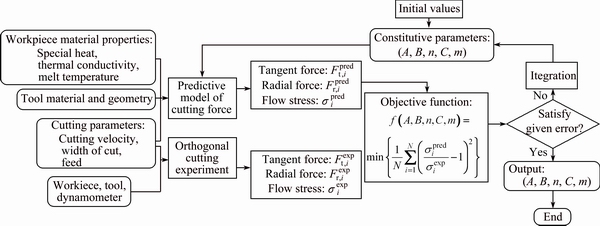
Fig. 6 Flow chart of identifying Johnson-Cook constitutive parameters for NAB material in machining

Fig. 7 Experiment setup for orthogonal cutting
Table 2 Designed parameters and experimental results
According to the flow chart in Fig. 6, the identification of constitutive parameters for NAB in machining can be summarized as follows.
1) With the initial values identified from compression test in Section 3, let A and B as the constants, n, C, and m as the variables, and set a certain increment.
2) Given the same cutting parameters, the predictive tangent force, radial force and flow stress 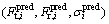 were calculated using the predictive model of cutting force, and the experimental ones
were calculated using the predictive model of cutting force, and the experimental ones 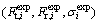 were obtained from the orthogonal cutting experiment and Eqs. and . Equation was the objective function. In the subsequent iterative cycle, the algorithm would automatically adjust the constitutive parameters.
were obtained from the orthogonal cutting experiment and Eqs. and . Equation was the objective function. In the subsequent iterative cycle, the algorithm would automatically adjust the constitutive parameters.
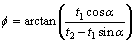 (3)
(3)
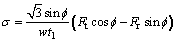 (4)
(4)
 (5)
(5)
where f is the shear angle; t1 is the depth of cut which is equal to feed; t2 is the chip thickness; α is the rake angle; w is the width of cut; N is the experiment number.
3) Based on the PSO algorithm, when the difference of flow stress between the predictive model and experiment was within the given error, the algorithm was stopped and outputted parameters A, B, n, C and m, which was the optimization solution.
Table 3 Johnson-Cook constitutive parameters for NAB in machining

The entire algorithm was implemented on the software MATLAB 8.0. Table 3 shows the results of constitutive parameters of Johnson-Cook model for NAB in machining.
5 Parameters validation
In order to verify the accuracy of the identified Johnson-Cook constitutive parameters, under the same conditions (material properties, cutting tool geometry, cutting parameters) shown in Table 4, the software AdvantEdge was used to simulate the orthogonal cutting process of the NAB material. And the results of cutting forces between the predictive model and simulation were compared. It can be seen from Fig. 8 that the predicted values had a good agreement with the simulation ones. The maximum error was within 15%, which indicated that the identified constitutive parameters of Johnson-Cook model for the material NAB was sufficiently accurate.
Table 4 Cutting condition in simulation and prediction
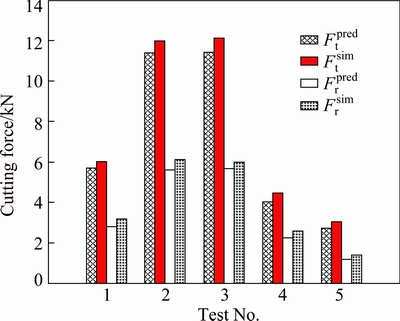
Fig. 8 Comparison of cutting forces between predictive model and simulation (Ft: Tangent force; Fr: Radial force)
6 Conclusions
1) The NAB material presented obvious effect of strain rate strengthening and thermal softening, and at different strain rates and temperatures, the effect showed small change.
2) The constitutive parameters of Johnson-Cook model for the NAB material in machining were identified based on the combination of SHPB tests, predictive cutting force model and orthogonal cutting experiment. The corresponding Johnson-Cook model was
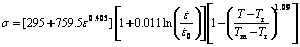 .
.
3) For the parameter validation, the maximum error between predicted and simulation results was within 15%, which showed that the identified constitutive parameters presented high accuracy.
Acknowledgement
The authors would like to thank Qi WEI for SHPB tests in Tsinghua University, China.
References
[1] CARTON J S. Marine propellers and propulsion [M]. 3rd ed. London: Butterworth-Heinemann, 2012.
[2] AL-HASHEM A, RIAD W. The role of microstructure of nickel-aluminium-bronze alloy on its cavitation corrosion behavior in natural seawater [J]. Materials Characterization, 2002, 48(1): 37-41.
[3] ANANTAPONG J, UTHAISANGSUK V, SURANUMTCHAI S, MANONUKUL A. Effect of hot working on microstructure evolution of as-cast nickel aluminum bronze alloy [J]. Materials & Design, 2014, 60: 233-243.
[4] WHARTON J A, BARIK R C, KEAR G, WOOD R J K, STOKES K R, WALSH F C. The corrosion of nickel-aluminum bronze in seawater [J]. Corrosion Science, 2005, 47: 3336-3367.
[5] THOSSATHEPPITAKA B, UTHAISANGSUKB V, MUNGSUNTISUKC P, SURANUNTCHAIA S, MANONUKULD A. Flow behavior of nickel aluminium bronze under hot deformation [J]. Materials Science and Engineering A, 2014, 604: 183-190.
[6] SARTKULVANICH P. Flow stress determination in metal cutting: Review of the literature and flow stress database [D]. Ohio: The Ohio State University, 2001.
[7] SEDIGHI M, KHANDAEI M, SHOKROLLAHI H. An approach in parametric identification of high strain rate constitutive model using Hopkinson pressure bar test results [J]. Materials Science and Engineering A, 2010, 527: 3521-3528.
[8] LI Y J, LI Q, WU A P, MA N X, WANG G Q, MURAKAWA H, YAN D Y, WU H Q. Determination of local constitutive behavior and simulation on tensile test of 2219-T87 aluminum alloy GTAW joints [J]. Transactions of Nonferrous Metals Society of China, 2015, 25(9): 3072-3079.
[9] LIU Wen-hui, HE Zhen-tao, CHEN Yu-qiang, TANG Si-wen. Dynamic mechanical properties and constitutive equations of 2519A aluminum alloy [J]. Transactions of Nonferrous Metals Society of China, 2014, 24(7): 2179-2186.
[10] PUJANA J, ARRAZOLA P J, SAOUBI R M, CHANDRASEKARAN H. Analysis of the inverse identification of constitutive equations applied in orthogonal cutting process [J]. International Journal of Machine Tools and Manufacture, 2007, 47: 2153-2161.
[11] SHATLA M, KERK C, ALTAN T. Process modeling in machining. Part I: Determination of flow stress data [J]. International Journal of Machine Tools and Manufacture, 2001, 41: 1511-1534.
[12] SARTKULVANICH P, KOPPKA F, ALTAN T. Determination of flow stress for metal cutting simulation-a progress report [J]. Journal of Materials Processing Technology, 2004, 146: 61-71.
[13] LEI S, SHIN Y C, INCROPERA F P. Material constitutive modeling under high strain rates and temperatures through orthogonal machining tests [J]. Journal of Manufacturing Science and Engineering, 1999, 121: 577-585.
[14] SHI B, ATTIA H, TOUNSI N. Identification of material constitutive laws for machining—Part II: Generation of the constitutive data and validation of the constitutive law [J]. Journal of Manufacturing Science and Engineering, 2010, 132: 051009.
[15] TOUNSI N, VINCENTI J, OTAO A, ELBESTAWI M A. From the basic mechanics of orthogonal metal cutting toward the identification of the constitutive equation [J]. International Journal of Machine Tools and Manufacture, 2002, 42(12): 1373-1383.
[16] OZEL T. Investigation of high speed flat end milling process [D]. Ohio: The Ohio State University, 1998.
[17] SHROT A,  M. Determination of Johnson-Cook parameters from machining simulations [J]. Computational Materials Science, 2012, 52: 298-304.
M. Determination of Johnson-Cook parameters from machining simulations [J]. Computational Materials Science, 2012, 52: 298-304.
[18] FU Zhong-tao, ZHANG Xiao-ming, WANG Xue-lin, YANG Wen-yu. Analytical modeling of chatter vibration in orthogonal cutting using a predictive force model [J]. International Journal of Mechanical Sciences, 2014, 88: 145-153.
镍铝青铜切削加工本构模型参数辨识
付中涛1,杨文玉1,曾思琪2,郭步鹏1,胡树兵2
1. 华中科技大学 机械科学与工程学院 数字制造装备与技术国家重点实验室,武汉 430074;
2. 华中科技大学 材料科学与工程学院,武汉 430074
摘 要:镍铝青铜材料因具有较高的强度、耐磨损及优异的抗应力腐蚀特性而广泛用于螺旋桨的制造中。为了建立其在高应变率条件下的本构关系,提出一种切削加工过程中Johnson-Cook模型参数辨识的新方法。该方法综合了SHPB动态压缩实验、可预测切削力模型及直角切削实验。首先,根据SHPB实验得到镍铝青铜在不同应变率和温度下的真实流变应力-应变曲线;然后,建立关于预测流变应力和实验流变应力的目标函数,将SHPB实验辨识的本构参数作为初值,采用PSO算法反演得到最终的本构参数;最后,对可预测切削力模型和有限元仿真获得的切削力进行对比,验证了所辨识参数的准确性。
关键词:镍铝青铜;本构参数;Johnson-Cook模型;辨识方法
(Edited by Wei-ping CHEN)
Foundation item: Project (2014CB046704) supported by the National Basic Research Program of China; Project (2014BAB13B01) supported by the National Science and Technology Pillar Program of China
Corresponding author: Wen-yu YANG; Tel: +86-27-87548180; E-mail: mewyang@hust.edu.cn
DOI: 10.1016/S1003-6326(16)64207-3