J. Cent. South Univ. (2012) 19: 187-192
DOI: 10.1007/s11771-012-0990-9
Try and error-based scheduling algorithm for cluster tools of wafer fabrications with residency time constraints
ZHOU Bing-hai(周炳海)1, LI Xin(李鑫) 2
1. School of Mechanical Engineering, Tongji University, Shanghai 201804, China;
2. Department of Systems Engineering and Engineering Management,City University of Hong Kong, Hong Kong, China
? Central South University Press and Springer-Verlag Berlin Heidelberg 2012
Abstract: To improve the productivity of cluster tools in semiconductor fabrications, on the basis of stating scheduling problems, a try and error-based scheduling algorithm was proposed with residency time constraints and an objective of minimizing Makespan for the wafer jobs in cluster tools. Firstly, mathematical formulations of scheduling problems were presented by using assumptions and definitions of a scheduling domain. Resource conflicts were analyzed in the built scheduling model, and policies to solve resource conflicts were built. A scheduling algorithm was developed. Finally, the performances of the proposed algorithm were evaluated and compared with those of other methods by simulations. Experiment results indicate that the proposed algorithm is effective and practical in solving the scheduling problem of the cluster tools.
Key words: cluster tools; residency constraints; scheduling model; algorithm; simulation experiments
1 Introduction
Cluster tools [1-3], which are complex in the configuration and prohibitively expensive in cost, have been increasingly used for most of wafer fabrication processes. Consequently, to schedule and control cluster tools in more defective and practical methods to improve the overall equipment efficiency (OEE) has become significant tasks to conquer for semiconductor manufacturing factories [4].
In terms of scheduling models, most research was based on diverse advanced Petri net models. WU et al [5-6] presented necessary and sufficient schedulability conditions for cluster tools by developing a resource-oriented Petri net-based scheduling model. MORRISON [7] developed a reduced complexity recursion for the wafer residency in each module based on flow line models, but moving times of wafers between modules were ignored. LEE and PARK [8] developed a new technique to model scheduling problems with residency time constraints and presented necessary and sufficient conditions to avoid deadlocks. KIM et al [9] proposed an extended Petri net for modeling the scheduling problem, and then, analyzed scheduling conflicts owing to residency time constraints and resource capacity constraints. SHIN et al [10] proposed a model-based approach based on finite state machines (FSMs) to develop a real-time scheduler for dual-armed cluster tools. The scheduler could cope with both normal operations and disturbances. Using Petri net models, LEE and LEE [11] proposed an open standard for specifying and exchanging the scheduling rules. However, both were based on scheduling policies and effective scheduling algorithms were not included.
In terms of scheduling algorithms, YIN [12] presented a heuristic algorithm based on try and error method, but permitted residency time of the incoming wafer was only used to eliminate resource conflict. CHAUVET et al [13] presented a low-complexity on-line scheduling algorithm for no-wait manufacturing systems with flexible processing time. However, the time required for transportation of jobs was not considered carefully. YOON and LEE [14] developed a real-time scheduling algorithm using the temporal constraint set to form the problem. The scheduling algorithm consisted of two procedures. TZENG et al [15] proposed a method of using multi-objective evolutionary algorithm (MEA) to obtain an optimal deadlock-free schedule during the flexible process of cluster tools. However, the method was only evaluated based on a simple instance instead of analysis of diverse complex instances.
According to related works mentioned above, most present researches only pay attention to scheduling wafer processes, and ignore resource conflicts caused by residency time constraints.
In this work, both resource capacity constraints and residency time constraints in cluster tools were carefully considered. A scheduling model was proposed following the definitions of residency time constraints. Relying on the model, a try and error-based scheduling algorithm was proposed, with an objective of minimizing completed time of the current inserting wafer.
2 Formulation of problem
According to SEMI Standard E21-96, a cluster tool is defined as an integrated, environmentally isolated and vacuumed manufacturing system consisting of process, transport, and cassette modules mechanically linked together. The principal components of a cluster tool are shown in Fig. 1. They are cassette modules to store raw/completed wafers, a single-arm/dual-arm robot to transport wafers from one process module to another (transport modules), and process modules that modify properties of the wafers, such as photolithography and etching equipment.

Fig. 1 Single-arm cluster tool
In order to form the precise problem domain of scheduling in cluster tools, definitions and assumptions are described as follows: 1) A process module cannot process multiple wafers at a time. 2) The transport module is composed of a single-arm robot, which cannot load, unload or transport multiple wafers at a time. 3) Multiple wafer types are produced in cluster tools. 4) The wafer may skip some process modules in the process. 5) There are residency time constraints for wafers. Wafers will be impaired or damaged if constraints are violated. 6) Process modules and transport modules are failure-free.
The objective of scheduling is to minimize the completed time of wafers to process in plan, to minimize the Makespan of the system.
Assume that there are M process modules in the cluster tool. To formulate the problem, the following notations are defined:
M—Number of process modules;
N—Number of wafers to be processed;
QJ—Permutation sequence of wafers where qh is the h-th wafer that enters the cluster tool for processing,
QJ=(q1, q2, …, qh, …, qN);
k—Wafer number, k=1, 2, …, N;
j—Process module number;
Jk—The wafer numbered k;
Pj—The process module numbered j;
tL—Loading time of a wafer to a process module;
tU—Unloading time from a process module;
tC—Required time of a position change operation;
 —Required processing time of the wafer Jk for the i-th process step, 1≤i≤f(k);
—Required processing time of the wafer Jk for the i-th process step, 1≤i≤f(k);
f(k)—Number of steps of the wafer Jk;
 —The most permitted residency time after wafers completed in a process module;
—The most permitted residency time after wafers completed in a process module;
ψ(i, k)—The process module in which the i-th process step of wafer Jk is processed;
τ(j, k)—The order number of the wafer Jk in all wafers processed in process module Pj;
 —A set including all wafers worked in Pj;
—A set including all wafers worked in Pj;
 —A set including all process modules required by the wafer Jk;
—A set including all process modules required by the wafer Jk;
φ(m, j)—The wafer number related to the m-th wafer processed in Pj;
 —The operation process that the wafer Jk is processed in the process module Pψ(i, k) for the i-th process step;
—The operation process that the wafer Jk is processed in the process module Pψ(i, k) for the i-th process step;
 —The beginning time of
—The beginning time of  ;
;
 —The ending time of
—The ending time of  ;
;
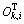 —The transporting operation that the wafer Jk is unloaded from the process module for preceding process module then moved and loaded in the process module Pψ(i, k) for the i-th process step using the transport module;
—The transporting operation that the wafer Jk is unloaded from the process module for preceding process module then moved and loaded in the process module Pψ(i, k) for the i-th process step using the transport module;
 —The beginning time of
—The beginning time of 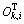 ;
;
 —The ending time of
—The ending time of 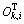 ;
;
 —The moving time of the transporting operation from Pj to Pl.
—The moving time of the transporting operation from Pj to Pl.
To simplify the problem reasonably, set q1=1, q2=2, …, qh=h, …, qN=N. A position change operation of a wafer, which puts a completed wafer in one process module into another module to process, exactly consists of a loading operation and an unloading operation. So
tC= tU+ tL (1)
In the work, assume that required time of the transporting operation between any two process modules is equivalent, thus  .
.
Since there is no intermediate buffer between process modules, the process operation begins when the wafer is loaded in the module. The following equations should be satisfied:
 (2)
(2)
 (3)
(3)
 (4)
(4)
The residency time constraints demand
 (5)
(5)
 (6)
(6)
As mentioned above, it is assumed that a process module cannot process multiple wafers at a time such that the process module must be free before a new wafer is inserted. The assumption demands
j=ψ(i, k) (7)
m=τ(j, k), m≥2 (8)
k′=φ(m-1, j) (9)
i′=η(k′, j) (10)
 (11)
(11)
Define  as a 0-1 variable:
as a 0-1 variable:
 (12)
(12)
The assumption that the transport module cannot operate multiple wafers at a time demands
 (13)
(13)
 (14)
(14)
where M′ is a large positive number.
The objective function of the scheduling model is
 (15)
(15)
Thus, the scheduling problem described above is transformed as a nonlinear programming problem with Eq. (15) as the objective and Eqs. (1)-(14) as constraints.
3 Scheduling algorithm
The scheduling problem of cluster tools with a single-arm robot as the transport module and two process modules has been proved to be NP-hard problems. Thus, it is extraordinarily complex even impossible to dead with the problem using mathematical analytic methods. In order to solve the problem formulated above in an effective and computable method, a try and error-based scheduling algorithm is proposed. It schedules wafers one by one. The scheduling algorithm has two phases. During the first phase, assume that there are neither conflicts of resources nor residency time constraints such that process modules and transport modules are available at any time, and then a basic schedule is built by setting the inserting wafer at earliest time in each process module. The second phase detects the conflict of any recourse in the basic schedule. If there are conflicts, the basic schedule is regulated to resolve conflicts on the basis of two conflictive avoid policies. At last, a feasible schedule is built. Figure 2 shows the algorithm flow chart. Two conflict avoid policies are named residency policy and delay policy. Residency policy makes the wafer stay in the process module for a period of time to eliminate recourse conflicts. Delay policy means delaying the beginning time of inserting a wafer into cluster tools to eliminate recourse conflicts.

Fig. 2 Flowchart of try and error based algorithm
Step 1: Install related parameters, such as N, ,
,  , ψ(k, j), f(k), φ(l, j), tM, tC, M, η(k, j). Set k=0.
, ψ(k, j), f(k), φ(l, j), tM, tC, M, η(k, j). Set k=0.
Step 2: Set k=k+1. If k>N, then turn to Step 9.
Step 3: Let  denote the entry time of the wafer Jk, and then build the basic schedule using
denote the entry time of the wafer Jk, and then build the basic schedule using
 ,
,  (16)
(16)
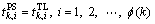 (17)
(17)
 (18)
(18)
 (19)
(19)
 (20)
(20)
Step 4: Start the second scheduling phase, and detect any recourse conflicts in the basic schedule. If there are conflicts, regulate the basic scheduling to eliminate conflicts on the basis of residency policy and compute results according to Eqs. (16)-(22).
Assume that a conflict occurs in the process module Pj for the wafer Jk, related to the process operation  and transport operation
and transport operation . If the conflict results from capacity constraints of process module, then set m=τ(j, k), m≥2, k′=φ(m-1, j), i′=η(k′, j). When the conflict could be eliminated via making the wafer Jk stay in Pj related to
. If the conflict results from capacity constraints of process module, then set m=τ(j, k), m≥2, k′=φ(m-1, j), i′=η(k′, j). When the conflict could be eliminated via making the wafer Jk stay in Pj related to  , if
, if

 (21)
(21)
Then
 (22)
(22)
where td denotes the stay time of the wafer in the process module to eliminate the conflict.
When staying the wafer in the process module related to  cannot eliminate the conflict, set k′=k-1 and consider the conflict caused by the preceding wafer. When the conflict could be eliminated via making the wafer Jk′ stay in the process module related to
cannot eliminate the conflict, set k′=k-1 and consider the conflict caused by the preceding wafer. When the conflict could be eliminated via making the wafer Jk′ stay in the process module related to  , if
, if

 (23)
(23)
then

 (24)
(24)
Regulate the schedule to eliminate conflicts and compute results according to Eqs. (16)-(20) and (23)-(24).
Step 5: If the conflict cannot be eliminated on the basis of residency policy, then eliminate it using delay policy and calculate results according to Eqs. (25)-(26). Return Step 4.
Let tD denote the delay time of the starting processing time of inserting wafer in the cluster tool:

 (25)
(25)
 (26)
(26)
Step 6: If there is any recourse conflict caused by the capacity constraints of transport module, then regulate the schedule to eliminate conflicts and compute results according to Eqs. (16)-(20) and (23)-(24).
Step 7: If the conflict cannot be eliminated on the basis of residency policy, then eliminate it using delay policy and calculate results according to Eqs. (25) and (26). Turn to Step 4.
Step 8: Turn to Step 2.
Step 9: Complete the scheduling procedure and build the final feasible schedule.
A simple example is used to illustrate the process of the algorithm, especially the two policies. Set M=3, N=3, tC=1 s and tM=1 s. Processing times and most permitted residency times are listed in Table 1.
Table 1 Processing time and most permitted residency time

The basic schedules of J1 and J2 are shown in Fig. 3(a) from the terminal schedule. There are conflicts at P3. The residency policy is applied to eliminating them. The schedule result is shown in Fig. 3(b) as well.
The scheduling process of J3 is shown in Fig. 4. There are conflicts at P3. If the residency policy was applied to eliminating them, J3 required 5 s residency time at P2. However, the most permitted residency time is 4 s in fact. Thus, the delay policy was applied then. The schedule result is shown in Fig. 4(c) as well.

Fig. 3 Residency policy: (a) Basic schedules of J1 and J2; (b) Schedules of J1 and J2 based on residency policy
4 Simulation and analysis
To evaluate the proposed scheduling algorithm, algorithms in Refs. [12] and [16] are set as the Benchmark. According to the algorithm in Ref. [12], permitted residency time of wafers is ignored, and wafers move to the process module related to the next process step immediately while completed. The algorithm is noted as the ND algorithm (Not using Delay time). The algorithm in Ref. [11] is noted as the BE algorithm (Basic on Event) and the algorithm proposed in this work is noted as the TE algorithm (Try and Error).
Improvement rates of results of the TE algorithm compared with results of the ND (BE) algorithm is defined as follows:
 (27)
(27)
 (28)
(28)
For the same instance, TND, TBE and TTE denote the makespan using the ND, the BE and the TE algorithms, respectively.
A simulation program is developed based on a cluster tool with 8 process modules and 25 wafers to process. Processing times and most permitted residency times are randomly generated from a normal distribution (tP, tU~N(μ, σ2)) with μ=60 s, σ=5, 10, 15 and μ=40 s, σ=10. Moreover, tM=7 s and tC=4 s. For a special value of the standard deviation, the results are the mean of 15 instances with the same values of distribution parameters. The simulation process is implemented through the Visual C++ 6.0 on the IBM personal computer with 160 GB hard disk, 1 GB DDR2 memory and 2.00 GHz Intel core 2 CPU.

Fig. 4 Delay policy: (a) Basic schedules with J3 inserted; (b) Schedules with J3 inserted based on residency policy; (c) Schedules with J3 inserted based on delay policy
Figure 5 shows the results of the TE algorithm. The improvement rate (RND) changes in the similar direction during σ=5, σ=10 and σ=15. When the number of wafers is small, RTE is increased fast as wafers increase; when the number of wafers is large, RND is increased slowly, even unchanged, as wafers increased. On the other hand, if σ=5, RND is the lowest in the three cases, if σ=10, the highest case and σ=15, the middle case. During any case for the standard deviation, the improvement rate is always higher than 30% when the number of wafers is move than 20, such that RND>30%. The results indicate that the TE algorithm is effective for any discrete degree of processing times, especially an appropriate degree, since the algorithm using the permitted residency times more adequately.

Fig. 5 Relationship of R from TE with distribution of σ
Table 2 lists the comparison of TE algorithm with ND algorithm and BE algorithm respectively for 25 wafers (a lot). In any case, the TE algorithm is better than the BE algorithm to resolve the scheduling problem. The reason is that, the BE algorithm only makes use of the information of inserting wafer and does not change the schedule built before. The TE algorithm will regulate the previous schedule for the last wafer and use more information of schedule. As a result, it gets better results.
Table 2 Improvement rates of TE algorithm compared with ND algorithm and BE algorithm

5 Conclusions
1) The try and error-based heuristic algorithm proposed is effective and practical to resolve the scheduling problem of the cluster tools with residency time constraints, especially compared with the ND algorithm.
2) The TE algorithm achieves steady improvement rates compared with the ND algorithm while the number of wafers is large, eg. more than 22 in the simulation experiment.
3) The TE algorithm proposed always offers better performance for diverse processing time, especially for a proper distribution degree of processing time. According to the simulation example, the improvement rate is always greater than 30% for any standard deviation and it is greatest when σ=10.
4) From comparison with the BE algorithm, which is also an effective real-time scheduling algorithm for cluster tools with residency time constraints, the TE algorithm always achieves better performance for diverse processing time.
References
[1] van ZANT P. Microchip fabrication: A practical guide to semiconductor processing [M]. 5th Ed. New York: McGraw-Hill, 2004: 495-496.
[2] YI Jin-gang, DING Sheng-wei, SONG De-zhe, ZHANG Mike-tao. Steady-state throughput and scheduling analysis of multi-cluster tools: A decomposition approach [J]. IEEE Transactions on Automation Science and Engineering, 2008, 5(2): 321-336.
[3] ZHOU Bing-hai, PAN Qing-zhi, WANG Shi-jin, WU Bin. Modeling of a photolithography process in semiconductor wafer fabrication systems using extended hybrid Petri nets [J]. Journal of Central South University of Technology, 2007, 14(3): 393-398.
[4] LEE T E. A review of scheduling theory and methods for semiconductor manufacturing cluster tools [C]// Proceedings of 2008 Winter Simulation Conference. Austin, America, 2008: 2127-2135.
[5] WU Nai-qi, CHU Cheng-bin, CHU Feng, ZHOU Meng-chu. Modeling and schedulability analysis of single-arm cluster tools with wafer residency time constraints using petri net [C]// Proceedings of 2008 IEEE International Conference on Networking, Sensing and Control. Sanya, China, 2008: 84-89.
[6] WU Nai-qi, ZHOU Meng-chu. Analysis of wafer sojourn time in dual-arm cluster tools with residency time constraint and activity time variation [J].IEEE Transactions on Semiconductor Manufacturing, 2010, 23(1): 53-64.
[7] MORRISON J R. Regular flow line models for semiconductor cluster tools: A case of lot dependent process times [C]// Proceedings of the 5th Annual IEEE Conference on Automation Science and Engineering. Bangalore, India, 2009: 465-470.
[8] LEE T E, PARK S H. An extended event graph with negative places and tokens for time window constraints [J]. IEEE Transactions on Automation Science and Engineering, 2005, 2(4): 319-331.
[9] KIM J H, LEE H T, LEE H Y, PARK D B. Schedulability analysis of time-constrained cluster tools with bounded time variation by an extended Petri net [J]. IEEE Transactions on Automation Science and Engineering, 2008, 5(3): 490-503.
[10] SHIN Y H, LEE T E, KIM J H, LEE H Y. Modeling and implementing a real-time scheduler for dual-armed cluster tools [J]. Computers in Industry, 2001, 45(1): 13-27.
[11] LEE J H, LEE T E. An open scheduling architecture for cluster tools [C]// Proceedings of the 6th Annual IEEE Conference on Automation Science and Engineering. Toronto, Canada, 2010: 420-425.
[12] YIN Y. An algorithm for hoist scheduling problems [J]. International Journal of Production Research, 1994, 32(3): 501-516.
[13] CHAUVET F, PROTH J M, WARDI Y. Scheduling no-wait production with time windows and flexible processing times [J]. IEEE Transactions on Robotics and Automation, 2001, 17(1): 60-69.
[14] YOON H J, LEE D Y. Online scheduling of integrated single-wafer processing tools with temporal constraints [J]. IEEE Transactions on Semiconductor Manufacturing, 2005, 18(3): 390-398.
[15] TZENG J, LIU T, CHOU J. Applications of multi-objective evolutionary algorithms to cluster tool scheduling [C]// Proceedings of the First International Conference on Innovative Computing, Information and Control. Beijing, China, 2006: 531-534.
[16] LI Xin, ZHOU Bing-hai, LU Zhi-qiang. Scheduling algorithm for cluster tools of wafer fabrication based on events-driven [J]. Journal of Shanghai Jiaotong University, 2009, 43(6): 898-901. (in Chinese)
(Edited by YANG Bing)
Foundation item: Projects(71071115, 60574054) supported by the National Natural Science Foundation of China
Received date: 2010-12-01; Accepted date: 2011-03-15
Corresponding author: ZHOU Bing-hai, Professor, PhD; Tel: +86-13564164374; E-mail: bhzhou@tongji.edu.cn